Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.


80
Глава
2.
Математические
модели
вход-выход
и
объекта
управления
(рис.
2.21).
Пусть
объект
управления
описывается
оператор-
ным
уравнением
y(t) = Wo(p)u(t),
(2.132)
а
регулятор
представлен
выражением
u(t) =
K(p)y*(t),
(2.133)
где
y(t) -
выходная
переменная,
u(t) -
управляющее
воздействие,
y*(t) -
задаю
щее
воздействие
(вход
системы),
Wo(p)
и
К(р)
-
передаточные
функции
(интегро
дифференциальные
операторы).
у*
u
у
=--..f
К(р)
Н
Wo(p)
~
Рис.
2.21.
Разомкнутая
система
Используя
правило
построения
модели
последовательно
соединенных
блоков,
на
ходим
уравнение
y(t) = W(p)y*(t),
(2.134)
связывающее
выходную
переменную
y(t)
и
входную
переме,Нную
y*(t)
через
пере
даточную
функцию
разомкнутой
системы
W(p) = Wo(p)K(p).
Эта
передаточная
функция
может
быть
записана
в
виде
W(p) =
Ь(р)
,
а(р)
(2.135)
(2.136)
где
а(р),
Ь(р)
-
дифференциальные
операторы
соответствующих
степеней.
Тогда
уравнение
(2.134)
можно
привести
к
виду
a(p)y(t) = b(p)y*(t)
(2.137)
и
при
необходимости
переписать
в
стандартной
форме
(2.1).
Теперь
рассмотрим
замкнутую
систему
управления
(рис.
2.22),
т.
е.
систему,
представленную
объектом
управления
(2.132)
и
регулятором
отклонения
(см.
1.5.1):
u(t) = K(p)e(t),
e(t) y*(t) - y(t),
(2.138)
(2.139)
где
е
-
рассогласование
(отклонение).
Используя
правило
(2.125),
находим
модель
замкнутой
системы
в
виде
y(t) =
Ф(р)у*(t),
(2.140)

2.4.
Построение
моделей
вход-выход
81
у*
Е
U
У
~
К(Р)
н
Wo(Р)Т
Рис.
2.22.
Замкнутая
система
где
Ф(р)
-
передаточная
функция
замкнутой
системы,
определяемая
как
Ф(р)
= K(p)Wo(p) = W(p)
1 + K(p)Wo(p) 1 +
W(p)·
Учитывая
(2.136),
нетрудно
получить
Ь(р)
Ф(р)
=
а(р)
+
Ь(р)·
(2.141)
(2.142)
Сравнение
последнего
выражения
с
(2.136)
показывает,
что
замыкание
системы
приводит
к
изменению
знаменателя
ее
передаточной
функции
-
характеристиче
ского
полинома
системы,
а
следовательно,
и
корней
полинома
(полюсов
системы).

Глава
з.
Математические
модели
вход-состояние-выход
в
этом
разделе
рассматриваются
непрерывные
линейные
модели,
описывающие
связи
входов
и
выходов
управляемого
объекта
(динамической
системы)
в
виде
системы
дифференциальных
уравнений
l-го
порядка
(системы
в
форме
Коши)
с
использованием
промежуточных
переменных
-
nеременных
состояния.
Такой
способ
описания
является
ключевой
особенностью
метода
пространства
состо
яний,
обоснованного
и
получившего
развитие
в
работах
Л.
Заде
и
ч.
Дезоера,
Р.
Е.
Калмана,
л.
с.
Понтрягина,
В.
г.
Болтянского
И
др.
[14,
19,
35,
40].
Метод
предоставляет
широкие
возможности
формализации
процедур
анализа,
синтеза
и
автоматизации
проектирования
и
поэтому
занимают
центральное
место
в
совре
менной
теории
линейных
систем.
Аналогичные
модели
дискретных
динамических
систем
изучаются
в
8.l.3.
-3.1.
Понятие
пространства
состояний
и
модели
состояние-выход
3.1.1.
Переменные
состояния
Рассмотрим
автономную
динамическую
систему
(2.2)
с
выходом
y(t),
где
t
~
to.
Отметим,
что
для
автономной
системы
решение
у
= y(t)
содержит
только
свободную
составляющую.
Введем
в
рассмотрение
некоторые
переменные
(3.1)

3.1.
Понятие
пространства
состояний
и
модели
состояние-выход
83
определенные
при
t
2::
to
и
имеющие
начальные
значения
Хю
=
Xi(tO).
Дадим
следующее
определение
(см.
также
[2,
3,
14,
20]).
Переменными
состояния
автономной
динамической
системы
с
выходом
у
назы
ваются
независимые
переменные
Xi(t)
такие,
что
значение
выходной
переменной
y(t)
в
произвольный
момент
времени
t =
tl
2::
to
однозначно
определяется
числами
Хю
= Xi(t
O
).
х
~----Xl
~--Т-X2
~---.-xn
t
Состояние
системы
в
момент
времени
t
2::
to
характе
ризуется
полным
набором
переменных
состояния
Xi(t),
а
начальное
состояние
-
числами
Хю.
По
определе
нию,
зная
начальное
состояние
системы,
можно
един
ственным
образом
отыскать
значение
выходной
пере
мен
ной
у
в
любой
момент
времени
tl
> to:
(3.2)
Процедура
нахождения
значений
некоторой
функции
y(t)
для
будущих
моментов
времени
называется
прогнозированием,
или
предсказанием.
Возможность
предска
зания
является
естественным
требованием
качественного
управления,
что
опреде
ляет
важность
введенного
понятия
для
рассматриваемых
далее
в
п.
3.2
неавтоном
ных
(управляемых)
систем.
При
этом
отличительной
особенностью
переменных
состояния
является
то,
что
для
предсказания
поведения
системы
в
любой
момент
времени
t >
to
(и
управления
неавтономной
системой)
достаточно
информации
о
переменных
состояния
в
момент
to
и
не
требуется
знание
предыстории
процес
сов,
т.
е.
информации
о
функциях
Xi(t)
при
t <
to.
Последнее
служит
основанием
для
построения
процедур
(алгоритмов)
прогнозирования
(см.
[47]),
а
также
алго
ритмов
управления
динамическими
системами
по
текущим
значениям
переменных
состояния
(см.
п.
7.4).
С
другой
стороны,
для
неавтономных
систем
с
помощью
пе
ременных
состояния
устанавливается
однозначное
соответствие
между
входными
и
выходными
воздействиями
(см.
3.2.l).
В
качестве
переменных
состояния
автономной
системы
могут
быть
выбраны,
в
частности,
фазовые
переменные,
т.
е.
выходная
переменная
системы
y(t)
и
n - 1
ее
производная
y{i)
(t).
Введем
в
рассмотрение
переменные
(3.3)
с
начальными значениями
Выход
~тационарной
автономной
системы
(2.2),
т.
е.
свободная
составляющая
про
цесса
при
t
2::
to
=
О,
дЛЯ
случая
неравных
корней
характеристического
уравнения
определяется
формулой
(см.
п.
2.2)
n
у
= L
Cie
Pit
,
i=l
(3.4)

84
Глава
З.
Математические
модели
вход-состояние-выход
где
коэффициенты
C
i
зависят
от
начальных
значений
выходной
переменной
и
ее
производных,
или
с
учетом
введенных
обозначений:
Таким
образом,
поведение
рассматриваемой
системы
при
t
~
О
однозначно
опреде
ляется
начальными
значениями
переменных
xi
и,
следовательно,
по
определению
эти
переменные
являются
переменными
состояния.
Общее
число
переменных
состояния
равно
n,
т.
е.
равно
порядку
дифференциаль
ного
уравнения
(2.2).
Линейные
комбинации
и
другие
функции
от
переменных
xi,
дополняемые
к
уже
выбранному
набору,
не
являются
переменными
состояния,
так
как
не
отвечают
условию
независимости.
Учитывая
введенные
обозначения,
преобразуем
уравнение
(2.2)
к
нормальной
фор
ме
Коши.
Дифференцируя
по
времени
уравнение
(3.3)
и
подставляя
в
полученные
выражения
(3.3)
и
(2.2),
находим
так
называемые
уравнения
состояния
автоном
ной
системы
(3.5)
Выходная
переменная
y(t)
связана
с
переменными
состояния
тривиальным
выра
жением
(простейшим
уравнением
выхода)
у
(3.6)
Уравнения
состояния
(3.5)
и
выхода
(3.6)
представляют
собой
простейший
пример
модели
состояние-выход
(СВ).
Замечание
3.1.
Выбор
переменных
состояния
динамической
системы
неоднозначен.
В
качестве
таких
переменных
могут
быть
взяты
не
только
фазовые
переменные,
но
и
многие
физические
переменные
системы,
такие
как
перемещение,
скорость,
ток,
напряжение
и
т.
д.
(см.
п.
4.1),
а
также
n
других
независимых
функций
времени,
полученных
как
линейные
комбинации
фазовых
и/или
физических
переменных.
Естественно,
что
выбор
переменных
состояния
определяет
структуру
и
параме~
ры
модели
состояние-выход.
Кроме
указанного
выше
способа
построения
такой
модели
в
стандартной
форме
(3.5)-(3.6),
модель
СВ
может
быть
получена
как
совокупность
моделей
реальных
физических
процессов,
часто
соответствующих
элементарным
звеньям
l-го
порядка
(см
п.
2.3
и
4.1).

3.1.
Понятие
пространства
состояний
и
модели
состояние-выход
85
3.1.2.
Модели
состояние-выход
и
переходные
процессы
в
более
общем
случае
уравнения
состояния
автономной
системы
также
представи
мы
в
нормальной
форме
Коши,
т.
е.
в
виде
системы
однородных
дифференциальных
уравнений
all
x
l(t)
+ a12
x
2(t)
+
...
+
aln
x
n(t),
а21Хl
(t)
+
a22x2(t)
+
...
+
a2nxn(t),
(3.7)
Xn(t)
где
t
~
t
o
,
Xi(tO)
=
XiO,
aij -
постоянные
или
зависящие
от
времени
вещественные
коэффициенты
(параметры),
а
уравнение
выхода,
связывающее
выходную
перемен
ную
системы
y(t)
с
переменными
Xi(t),
имеет
вид
(3.8)
где
ci -
коэффициенты
(параметры).
Нетрудно
показать
(см.
ниже),
что
перемен
ные
Xi(t)
действительно
являются
переменными
состояния,
и
поэтому
уравнения
(3.7)
и
(3.8)
представляют
наиболее
общую
модель
состояние-выход
линейной
ав
тономной
динамической
системы
с
одним
выходом.
Вектор
Х
= x(t)
размерности
71"
элементами
которого
являются
переменные
состояния
Xi
= Xi(t),
т.
е.
(3.9)
называется
вектором
состояния.
Вектор
Х
является
элементом
n-мерного
линейного
(векторного)
простран
ства
IRn,
которое
называется
nространством
состоя
ний:
Х
Е
IRn
[14].
Теперь
уравнения
(3.7)-(3.8)
можно
записать
в
векторно-матричной
форме:
X(t)
=
Ax(t),
y(t)
=
Cx(t),
где
x(t
o
) =
ХО
=
{XiO}
-
вектор
начальных
состояний
(начальных
условий),
А
(3.10)
(3.11)

86
Глава
З.
Математические
модели
вход-состояние-выход
-
матрица
системы
размера
n
х
n,
с
=
{C'i}
= I
Cl
С2
...
Сп
1
-
матрица
размера
1
х
n
(см.
[9,
21]).
В
частном
случае,
когда
уравнения
модели
ВС
представлены
в
виде
(3.5)-{3.6),
получаем
о
1
О
О
О
О
1
О
А
С
1 1
О
О
...
о
1.
о о
о
1
-а
n
-an-l
-а
n
-2
-al
Решением
системы
(3.7)
с
начальными
условиями
Xi(t
o
) =
Хю
называется
набор
функций
(3.12)
которые
при
t =
to
удовлетворяют
начальным
условиям,
а
для
любых
t
~
to
-
уравнениям
(3.7).
Соответственно,
решением
системы
(3.l0)
будет
вектор-функция
X(t)
= x(t,
Ха,
to).
(3.13)
Решение
может
быть
представлено
как
X(t)
=
Ф(t,
to)xo,
(3.l4)
где
Ф(t,
t
o
) -
фундаментальная
(nереходная)
матрица
системы
(3.10).
Подстав
ляя
(3.14)
в
уравнение
выхода
(3.11),
получаем
выражение
для
расчета
выходной
переменной
y(t) =
СФ(t,
to)Xo.
(3.15)
Для
рассматриваемых
далее
стационарных
систем
переходная
матрица
находится
как
Ф(t,
to)
=
eA(t-tо).
(3.16)
Полагая
to
=
О,
получаем:
(3.17)
и
(3.18)
Замечание
3.2.
Анализ
уравнений
(3.l4)-{3.15)
и
(3.17)-(3.18)
показывает
следу
ющее.
1.
Переменные
Xi(t)
и
выходная
переменная
y(t)
в
любой
момент
времени
t
~
to
однозначно
определяются
n
начальными
значениями
Хю
и,
следовательно,
по
определению
переменные
Xi
действительно
являются
переменными
состоя
ния.
3.1.
Понятие
пространства
состояний
и
модели
состояние-выход
87
2.
Предыстория
системы
(ее
движение
при
t <
to)
не
влияет
на
поведение
системы
при
t
~
to.
Если
для
некоторых
начальных
условий
и
любых
t
~
to
имеет
место
тождество
x(t)
=
х*,
(3.19)
где
х*
= const,
то
значение
х
=
х*
называется
равновесным
состоянием,
или
положением
равновесия,
автономной
системы
(3.10).
Очевидно,
что
в
равновесном
состоянии
выполняется
х
=
о
(3.20)
и,
следовательно,
Ах*
=
О.
(3.21)
При
условии,
что
det
А
=1=-
О,
получаем,
что
единственным
положением
равновесия
системы
(3.10)
является начало
координат
пространства
состояний
IRn,
т.
е.
х*
=
О,
а
при
det
А
=
О
существуют
нетривиальные
множества
равновесных
состояний
(прямые,
плоскости),
т.
е.
подпространства,
удовлетворяющие
уравнению
(3.21).
После
подстановки
х*
=
О
в
уравнение
выхода
(3.11)
находим
равновесное
значение
выходной
переменной
(см.
2.2.2)
у*
=
О.
Формулы
(3.17)-(3.18)
определяют
переходные
процессы
системы
- n
функций
времени
Xi(t).
Графически
они
могут
быть представлены
в
виде:
•
временных
диаграмм
(см.
п.
2.2);
•
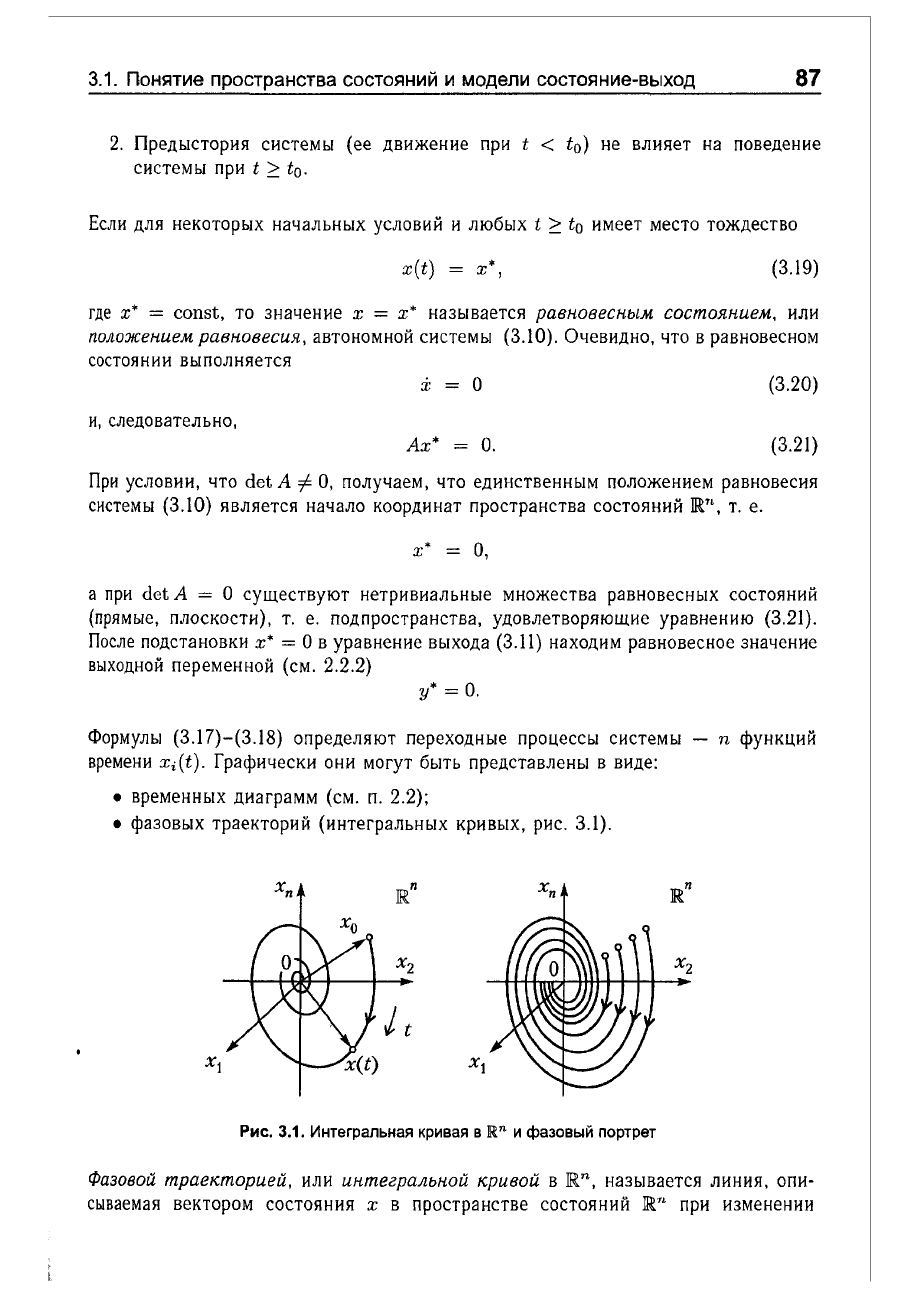
фазовых
траекторий
(интегральных
кривых,
рис.
3.1).
Рис.
3.1.
Интегральная
кривая
в
IRn
и
фазовый
портрет
Фазовой
траекторией,
или
интегральной
кривой
в
IRn,
называется
линия,
опи
сываемая
вектором
состояния
х
в
пространстве
состояний
IRn
при
изменении

88
Глава
З.
Математические
модели
вход-состояние-выход
переменной
t
Е
[to,
tf),
tf
>
to,
т.
е.
годограф
вектор-функции
х(ха,
t)
по
па
раметру
t.
Фазовый
портрет
-
это
множество
фазовых
траекторий,
соответствующих
раз
личным
значениям
начальных
условий
ха
(см.
рис.
3.1).
Введенные
выше
понятия
обобщаются
на
класс
многоканальных
(многосвязных,
см.
2.1.3)
систем,
которые
характеризуются
несколькими
выходными
переменными
щ,
j =
1,
т.
Общая
модель
многоканальной
системы
включает
уравнения
состоя
ния
(3.7)
и
m
уравнений
выхода:
Уl
-
Сll
Х
l
+
С12
Х
2
+ ... +
Сlп
Х
п,
У2
С21
Х
l
+
С22
Х
2
+ ... +
С2п
Х
п,
(3.22)
Yrп
-
C
rп
l
X
l
+
C
rп
2
X
2
+ ... +
CrппX
п
,
где
Cji
-
вещественные
коэффициенты
(параметры).
Определим
т-мерный
вектор
выходов
у=
Уl
У2
Уm
(3.23)
как
вектор
пространства
выходных
переменных
n:t
тn
и
запишем
уравнение
(3.22)
в
компактной
векторно-матричной
форме
у=Сх,
(3.24)
где
С
=
{Cij}
-
матрица
размера
m
х
n.
Таким
образом,
модель
состояние-выход
многоканальной
системы
представлена
уравнениями
(3.7), (3.22)
или
векторна
матричными
уравнениями
(3.10)
и
(3.24).
3.1.3.
Свойства
моделей
состояние-выход
Проанализируем
свойства
модели
(3.10)-(3.11)
и
связанные
с
ними
решения
-
пе
реходные процессы
(3.17)-(3.18)
(см.
также
[2,3,10,20]).
Прежде
всего
определим
следующие
алгебраические
объекты:
•
характеристический
полином
матрицы
состояния
А:
(3.25)

3.1.
Понятие
пространства
состояний
и
модели
состояние-выход
89
•
собственные
значения
(собственные
числа)
матрицы
А
как
n
чисел
Лi{А},
являющихся
корнями
полинома
(3.25);
•
собственные
векторы
матрицы
Ti{A};
а
также
(для
случая
вещественных
собственных
чисел
Лi
=1
Лj)
-
собственные
подпространства
как
множе
ства
(прямые,
плоскости
и
т.
д.)
(3.26)
где
л
-
вещественные
числа.
Напомним,
что
в
рас
сматриваемом
случае
собственные
векторы
удовлетво
ряют
уравнениям
(3.27)
Введем
в
рассмотрение
диагональную
матрицу
и
из
выражения
(3.27)
найдем:
Т
n
I
А.
(3.28)
Выражение
(3.28)
устанавливает
связь
матрицы
системы
А
с
диагональной
матри
цей
Л.
Квадратная
матрица
называемая
матрицей
подобия,
в
рассматриваемом
здесь
случае
вещественных
некратных
корней
не
вырождена
и,
следовательно,
имеет
место
следующее
поло
жение.
Свойство
3.1.
Матрица
А
приводима
к
диагональной
форме:
л
=
т-
1
АТ.
(3.29)
в
более
общем
случае
матрица
А
может
быть
приведена
к
так
называемой
жорда
н,овой
(блочно-диагональной)
форме,
т.
е.
найдется
невырожденная
матрица
пре
образования
Т
такая,
что
J =
Т-
1
АТ.
(3.30)
