Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.


50
Глава
2.
Математические
модели
вход-выход
значений
(см.
п.
1.1).
Так,
входным
сигналом
САУ
служит
задающее
воздействие
y*(t),
а
выходным
переменная
y(t).
При
описании
блоков
часто
применяются
и~)
~
обозначения
X2(t)
и
Xl(t)
соответственно.
В
дальнейшем
воспользуемся
обозначениями,
характерными
для
объекта
управления,
где
входным
сигналом
является
управляющее
воздействие
u(t),
а
выходным
-
регулируемая
переменная
y(t).
2.1.1.
Аналитические
модели
Линейная
модель
вход-выход
одноканальной
динамической
системы
(здесь
-
объ
екта
управления)
может
быть
представлена
обыкновенным
дифференциальным
уравнением
[21]
вида:
аоу(n)
+
aly(n-l)
+
...
+
an-1Y
+
аnу
=
=
Ьои(,т)
+
b1u(Jn-l)
+
...
+
brn-1u
+
Ьrnи,
(2.1)
где
Щ,
b
i
-
коэффициенты
(параметры
модели),
аа
>
О,
Ь
а
>
О,
n -
порядок
модели,
О
:::;
m < n.
Уравнение
(2.1)
связывает
входные сигналы
u(t)
и
их
произ
водные
u(i)(t)
с
выходными
сигналами
y(t)
и
их
производными
y(i)(t)
на
некото
ром
временном
интервале,
т.
е.
при
t
Е
[ta,
tf].
Значения
y(ta) =
Уа,
iJ(ta)
=
Уа'
...
'
y(n-l)(ta)
=
Y6
n
-
1
)
называются
начальными
значениями
(условиями),
а
число
r = n - m
~
1 -
относительной
степенью
модели.
Различают
стационарные
системы,
для
которых
значения
параметров
неизменны:
ai = const , b
i
= const,
и
можно
положить
ta
=
О,
и
нестационарные
модели,
где
пара
метры
являются
функциями
времени,
т. е.
ai = ai(t), b
i
= bi(t).
В
случае
когда
аа
=
1,
уравнение
(2.1)
называется
nриведенным.
Система,
для
которой
u(t)
==
О,
называется
автономной.
Описание
автономной
системы
дается
однородным
дифференциальным
уравнением
вида
(n)
+
(n-l)
+ + . +
о
аоу
alY
. • .
an-1Y
аnу
= .
(2.2)
Модель
(2.1)
может
быть
переписана
в
операторной
форме.
Для
этого
введем
в
рассмотрение
оператор
дифференцирования
d
Р
= dt
и
положим,
что
С
учетом
введенных
обозначений
уравнение
(2.1)
легко
преобразуется
к
оператор
ной
форме
a(p)y(t)
=
b(p)u(t),
(2.3)

2.1.
Линейные
модели
вход-выход
где
используются
дифференциальные
операторы
а(р)
=
аорn
+ a1pn-l + ... +
an-lР
+
а
n
,
Ь(р)
=
ьорn
+ b1pn-l + ... + bn-1p +
Ь
N
•
51
(2.4)
(2.5)
Оператор
а(р)
называется
характеристическим
полиномом
ДИфференциального
уравнения
(2.1),
а
комплексные
числа
Pi, i =
1,
n ,
являющиеся
корнями
характе
ристического
уравнения
а(р)
=
О,
(2.6)
называются
полюсами
системы
(2.1).
Дифференциальный
оператор
Ь(р)
-
харак
теристический
полином
правой
части.
Корни
уравнения
Ь(р)
=
О,
(2.7)
т.
е.
комплексные
числа
Р?,
i =
1,
m ,
называются
нулями
системы
(2.1).
Из
уравнения
(2.3)
найдем
явную
связь
переменных
y(t)
и
u(t)
в
виде
операторного
уравнения:
y(t)
=
W(p)u(t),
где
интегрально-дифференциальный
оператор
W(p) =
Ь(р)
а(р)
называется
передаточной
функцией
системы
(2.1).
(2.8)
(2.9)
Преимущество
использования
операторных
моделей
типа
(2.3)
и
(2.8)
заключа
ется,
во-первых,
в
краткости
записи
соответствующих
уравнений,
а
во-вторых,
в
удобстве
преобразования
сложных
(составных)
моделей
(см.
п.
2.4).
Рассмотрим
частный
случай
динамической
системы
с
коэффициентами
Ь
О
=
Ь
1
=
==
...
= b
m
-
1
=
О.
При
Ь
т
=
Ь
i=
о
система
имеет
относительную
степень
r = n
-1,
и
нули
отсутствуют.
Уравнение
(2.1)
принимает
вид
(n)
+
(n-l)
+ + . + =
аоу
alY .
..
an-lУ
аnу
Ьu,
(2.10)
уравнение
(2.3) -
a(p)y(t) = bu(t),
(2.11)
а
уравнение
(2.8) -
y(t)
Ь
=
а(р)
u(t).
(2.12)

52
Глава
2.
Математические
модели
вход-выход
Прuмер
2.1.
Пусть
Ь(р)
=
Ь
и
n = 2 .
Дифференциальное
уравнение
системы
имеет
вид
(2.13)
с
начальными
условиями
у(О)
=
Уа,
у(О)
=
Уа.
Здесь
У
= dy/dt -
скорость
изме
нения
выходной
переменной.
Операторные
формы
модели
-
(2.14)
и
Ь
y(t) = 2 u(t).
аор
+
аlР
+
а2
(2.15)
Характеристическое
уравнение
системы
имеет
два
(вещественных
или
комплексно-сопряженных)
корня
аl
JaI
-
4а2
Рl,2
= - -
=F
....:......-=----
2а
а
2а
а
о
Пример
2.2.
Модели
вход-выход
нагревательной
печи,
RС-цепочки
и
разгона
элек
тродвигателя
(см.
пример
1.1)
описываются
ДИфференциальным
уравнением
пер
вого
порядка
TX2(t) + xz(t) =
Ku(t),
(2.16)
где
и
-
входное
воздействие
(напряжение),
Х2
-
выходной
сигнал
(температура,
выходное
напряжение
или
угловая
скорость
соответственно), Т,
К
-
постоянные
коэффициенты
(параметры).
u(t)
к
Тр+1
Операторная
форма
модели
имеет
вид
(Тр+
1)X2(t) = Ku(t).
(2.17)
Здесь
Тр
+ 1 =
О
-
характеристическое
уравнение,
которое
имеет
один
корень
(полюс
системы)
Рl
=
-l/Т.
Из
уравнения
(2.17)
находим
явную
связь
входа
и.
выхода
к
X2(t) =
Тр
+ 1 u(t).
(2.18)
2.1.
Линейные
модели
вход-выход
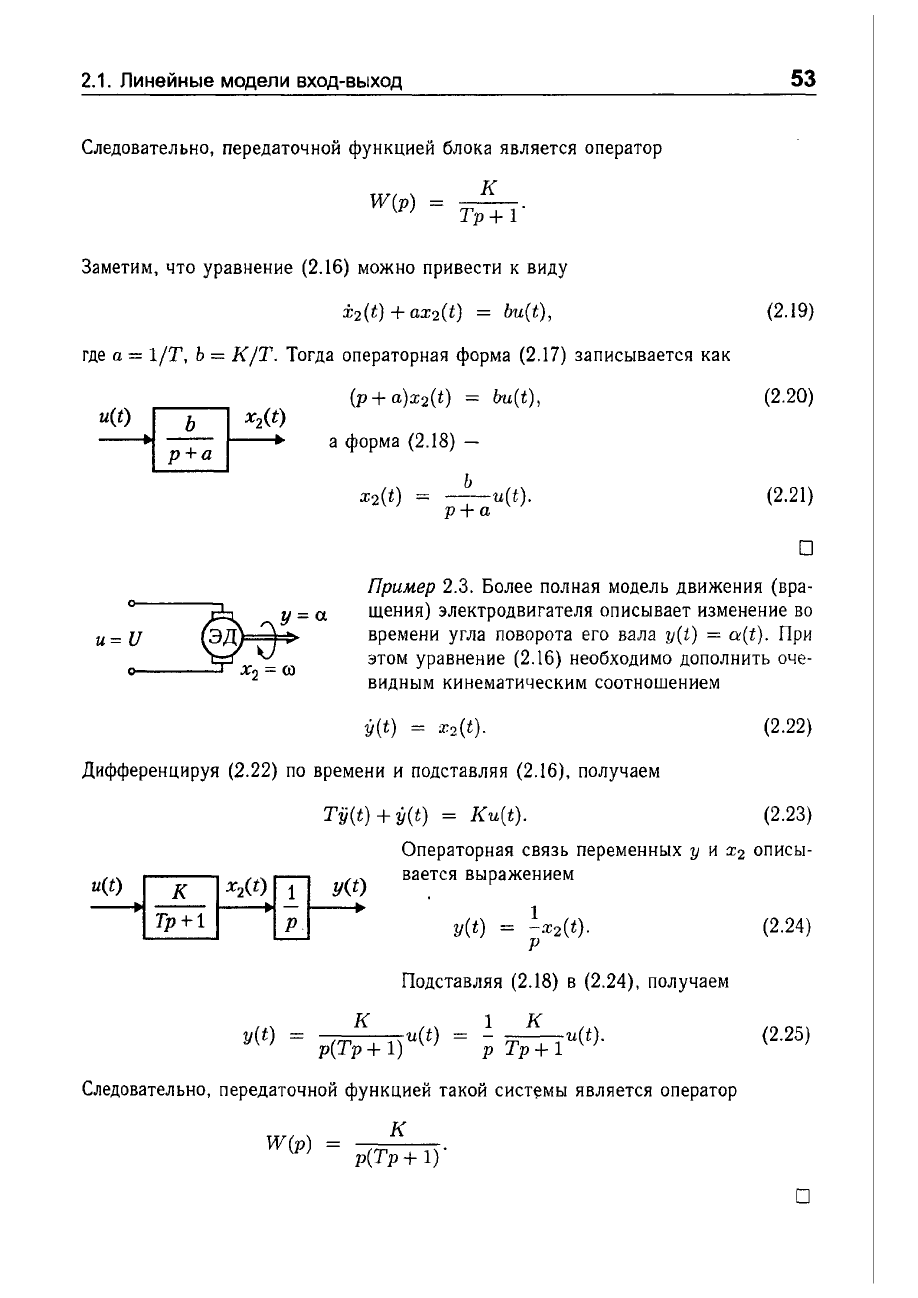
Следовательно,
передаточной
функцией
блока
является
оператор
к
W(p) =
Тр+
l'
Заметим,
что
уравнение
(2.16)
можно
привести
к
виду
xz(t) + aX2(t) = bu(t),
где
а
=
l/Т,
Ь
=
К/Т.
Тогда
операторная
форма
(2.17)
записывается
как
u(t)
ь
р+а
(р
+ a)x2(t) = bu(t),
а
форма
(2.18)
-
Ь
X2(t)
=
--u(t).
р+а
53
(2.19)
(2.20)
(2.21)
о
u
=~
о----
-----'~
=
а
Прuмер
2.3.
Более
полная
модель
движения
(вра
щения)
электродвигателя
описывает
изменение
во
времени
угла
поворота
его
вала
y(t) = a(t).
При
этом
уравнение
(2.16)
необходимо
дополнить
оче
видным
кинематическим
соотношением
(2.22)
Дифференцируя
(2.22)
по
времени
и
подставляя
(2.16),
получаем
Tjj(t) + y(t) =
Ku(t).
(2.23)
u(t)
к
Тр+1
y(t)
Операторная
связь
переменных
у
и
Х2
описы
вается
выражением
1
y(t) = -X2(t).
Р
Подставляя
(2.18)
в
(2.24),
получаем
К
1
К
y(t) =
р(Тр
+ 1) u(t) =
р
Тр
+ 1 u(t).
Следовательно,
передаточной
функцией
такой
сист~мы
является оператор
к
W(p) =
р(Тр
+
1)'
(2.24)
(2.25)
о

54
Глава
2.
Математические
модели
вход-выход
Прuмер
2.4.
Рассмотрим
поступательное
движение
материальной
точки
массы
т
под
действием
силы
(входного
воздействия)
u = F(t).
Данная
динамическая
си
стема
описывается
уравнением
второго
порядка
(2-м
законом
Ньютона)
и=Р
.
,
6
у
mjj(t) = u(t)
(2.26)
с
начальными
условиями
Уа
=
у(о),
Уо
=
у(о).
Здесь
y(t) -
линейное
перемещение.
Операторная
форма
модели
принимает
вид
mp2y(t) = u(t),
(2.27)
а
характеристическое
уравнение
системы
имеет
два
корня
(полюса
системы)
Рl,2
=
о.
функцией
блока
является
оператор
W(p)
Из
уравнения
(2.27)
находим
явную
связь
входа
и
выхода
ь
y(t) = 2"u(t),
р
(2.28)
где
Ь
=
1/11'1,.
Следовательно,
передаточной
Движение
вращательного
звена,
имеющего
момент
инерции
J,
под
действием
момента
сил
u = Al(t)
так
же
описывается
дифференциальным
уравнением
вто
рого
порядка
Jjj(t) = u(t),
(2.29)
где
y(t) -
угловое
перемещение.
В
силу
идентичности
последнего
выражения
и
уравнения
(2.26)
все
модели
поступательного
и
вращательного
движения
совпа
дают.
О
2.1.2.
Структурные
схемы
Наиболее
распространенной
графоаналитической
формой
модели
динамической
си
стемы
является
структурная
схема
-
разновидность
направленного
графа.
Эле
ментами
такой
схемы
являются:
2.1.
Линейные
модели
вход-выход
а
x(t)
---+
б
в
~
~
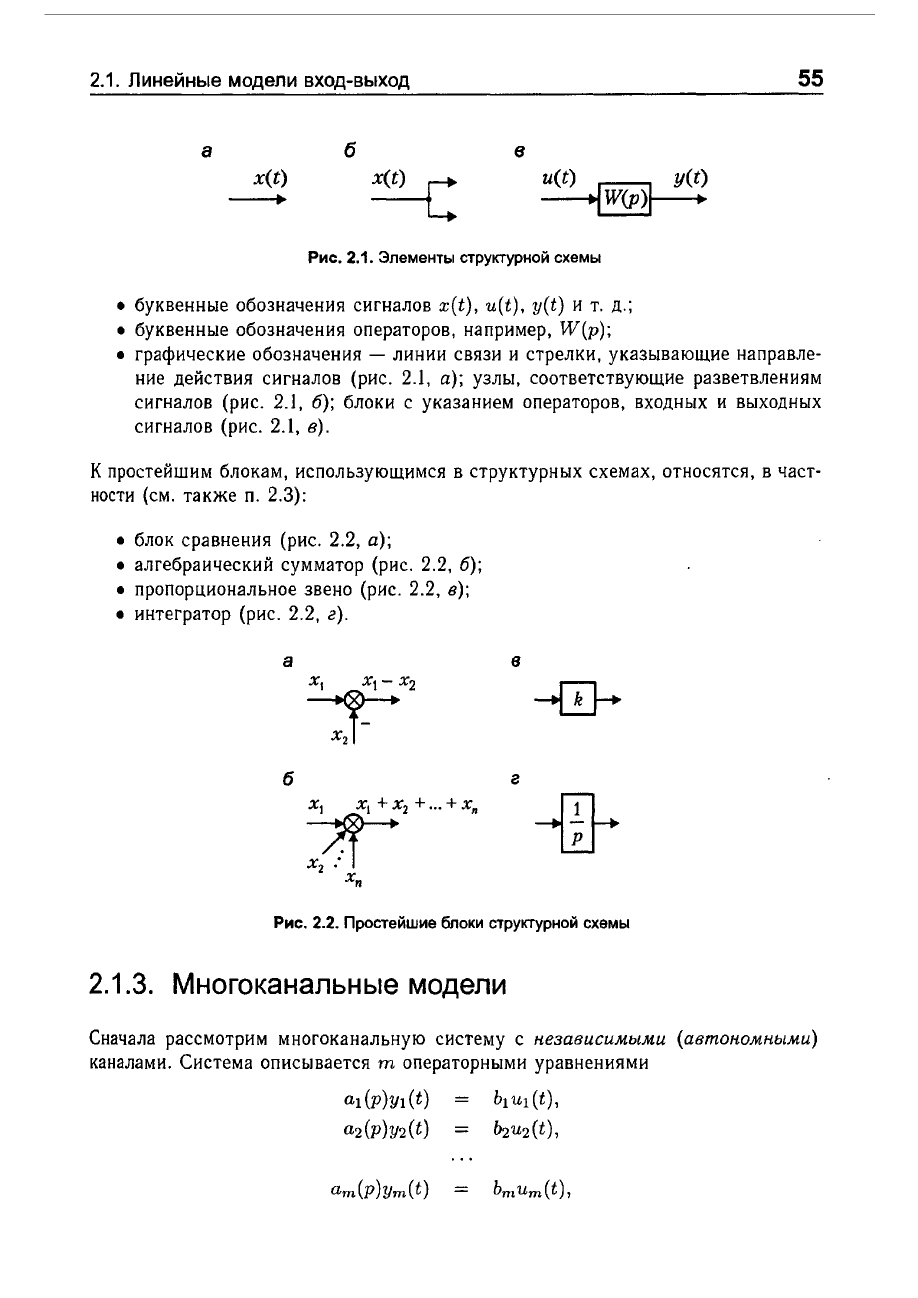
Рис.
2.1.
Элементы
структурной
схемы
•
буквенные
обозначения
сигналов
x(t), u(t), y(t)
и
т.
Д.;
•
буквенные
обозначения
операторов,
например,
W(p);
55
•
графические
обозначения
-
линии
связи
и
стрелки,
указывающие
направле
ние
действия
сигналов
(рис.
2.1,
а);
узлы,
соответствующие
разветвлениям
сигналов
(рис.
2.1,
б);
блоки
с
указанием
операторов,
входных
и
выходных
сигналов
(рис.
2.1,
в).
к
простейшим
блокам,
использующимся
в
структурных
схемах,
относятся,
в
част
ности
(см.
также
п.
2.3):
•
блок
сравнения
(рис.
2.2,
а);
•
алгебраический
сумматор
(рис.
2.2,
б);
•
пропорциональное
звено
(рис.
2.2,
в);
•
интегратор
(рис.
2.2,
г).
б
г
:а'
+:,+
...
+х.
-1Ir
х
n
Рис.
2.2.
Простейшие
блОКИ
структурной
схемы
2.1.3.
Многоканальные модели
Сначала
рассмотрим
многоканальную
систему
с
независимыми
(автономными)
каналами.
Система
описывается
т
операторными
уравнениями
al(p)Yl(t)
а2
(Р)У2
(t)
Ь
1
иl
(t),
= b
2
U
2(t),
56
Глава
2.
Математические
модели
вход-выход
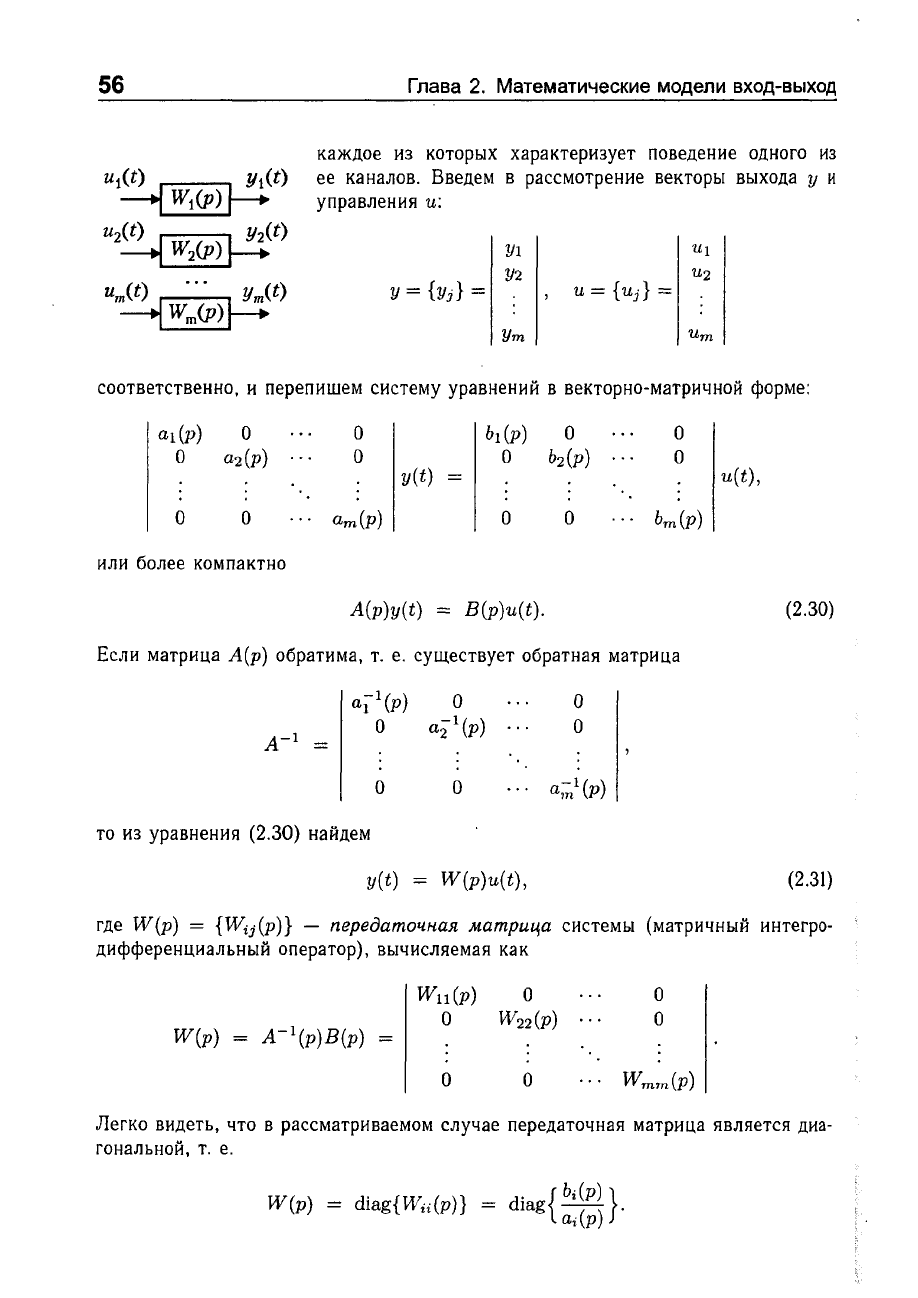
каждое
из
которых
характеризует
поведение
одного
из
ее
каналов.
Введем
в
рассмотрение
векторы
выхода
у
и
управления
и:
u = {Uj} =
Уm
соответственно,
и
перепишем
систему
уравнений
в
векторно-матричной
форме:
аl(Р)
О
О
Ь
1
(р)
О О
О
а2(Р)
О
О
bz(p)
О
y(t)
=
u(t),
О
О
аm(р)
О О
Ьт(р)
или
более
компактно
A(p)y(t) = B(p)u(t).
(2.30)
Если
матрица
А(р)
обратима,
т.
е.
существует
обратная
матрица
a
1
1
(p)
о
о
А-
1
О
а;:l(р)
О
=
О О
а;;/(р)
то
из
уравнения
(2.30)
найдем
y(t)
=
W(p)u(t),
(2.31)
где
W(p) =
{Wij(p)}
-
передаточная
матрица
системы
(матричный
интегро
дифференциальный
оператор),
вычисляемая
как
W(p)
W
l1
(p)
о
о
о
о
о
Легко
видеть,
что
в
рассматриваемом
случае
передаточная
матрица
является
диа
гональной,
т.
е.
W(p)
=
diag{Wii(p)}
= diag{
~:i:;}.

2.1.
Линейные
модели
вход-выход
57
Теперь
рассмотрим
многосвязную
систему.
т.
е.
многоканальную
систему
со
свя
занными
каналами.
описываемую
системой
операторных
уравнений
а11(Р)Уl
+ alZ(p)yz +
...
+
аlm(Р)Уm
=
Ь
11
(р)иl
+
...
+
Ь
1m
(р)и
1То
aZl(p)Yl + a2Z(p)yz +
...
+ azm(P)Ym =
Ь
21
(р)иl
+
...
+
Ь
2m
(р)и
m
,
Система
приводится
к
векторно-матричной
форме
(2.30),
где
а11
(Р)
а12(Р)
аlт(Р)
Ь
11
(Р)
Ь
12
(Р)
Ь
1т
(Р)
А(р)
=
aZl
(Р)
а22(Р)
а2m(Р)
,
В(Р)
=
Ь
21
(Р)
Ь
22
(Р)
Ь
2т
(Р)
а
т
l
(Р)
amz(p)
атm(р)
Ь
т1
(Р)
Ь
т2
(р)
Ьтm(Р)
и
форме
(2.31),
где
передаточная
матрица
W(p)
определяется
выражением
W(p) =
A-
1
(р)В(р)
Wmm(p)
Модель
(2.31)
можно
также
записать
в
скалярном
виде:
Уl
W
ll
(р)иl
+ W
12
(P)U2
+ ... + W
1m
(P)U
m
,
У2
W
21
(р)иl
+
W2
2
(p)U2
+
...
+ W
2m
(P)U
m
,
Отметим,
что
диагональные
операторы
Wii(p)
от
носятся
к
основным
каналам,
а
остальные
пере
даточные
функции
Wij(p), i
i=
j,
характеризуют
перекрестные
связи
многоканальной
системы.
Для
двухканальной
многосвязной
системы
(т
=
2)
получаем:
Уl
= W
ll
(р)иl
+ W
12
(p)U2,
У2
= W
21
(p)Ul
+ W
22
(p)U2,
где
W
ll
(p), W
22
(P)
-
передаточные
функции
основных
каналов
системы,
а
W12(P).
W
21
(p)
-
передаточные
функции
перекрестных
связей.

58
Глава
2.
Математические
модели
вхоДмвыхоД
2.1.4.
Модели
возмущенных
систем
f(t)
u(t;\l
y(t)
~
Возмущающее
воздействие
f(t),
характеризующее
влияние
на
объект
управления
внешней
среды
(см.
1.2.1),
рассмат
ривается
как
дополнительный
входной
сигнал.
Тогда
линей
ная
модель
одноканальной
динамической
системы
принима
ет
вид
(n)
+
(n-l)
+ + . +
аоу
аlУ
.""
a
n
-lУ
аnу
=
=
b
o
u(7n)
+ b
1
u(7n-l)
+ .. " + b
7n
-
1
u + b
7n
u +
d
f
(k) d
f(k-l)
d
f"
d f
+
о
+ 1 + " " . +
k-l
+ k ,
(2.32)
где
d
i
-
коэффициенты,
определяющие
влияние
на
процессы
в
системе
возмущения
f(t)
и
его
производных
f(i)(t), d
o
i=
о
,
о
~
k < n.
После
подстановки
операторов
дифференцирования
pi
и
соответствующих
преобразований
получаем
операторную
форму
модели
(2.32):
a(p)y(t)
=
b(p)u(t)
+
d(p)f(t),
(2.33)
где
используется
дифференциальный
оператор
d(p) = dopk +
d1pk-l
+ ... +
dk-1p
+ d
k
,
и
форму
y(t)
-
W(p)u(t)
+
W/(p)f(t),
(2.34)
где
W
(р)
= d(p)
f
а(р)
-
передаточная
функция
по
возмущающему
воздействию
f(t).
В
частном
случае,
когда
Ь
О
= b
1
=
..
, = b
m
-
1
=
О,
y(t)
Ь
m
=
Ь
i=
о,
и
do
= d
1
= ... = d
k
-
1
=
О,
d
k
= d
i=
о,
(Х).-.
модель
(2.32)
принимает
вид
аоу(n)
+
aly(n-l)
+ ... +
an-lУ
+
аnу
=
bu(t) + df(t),
(2.35)
модель
(2.33) -
a(p)y(t) = bu(t) + df(t),
(2.36)
а
модель
(2.34) -
y(t)
Ь
d
=
а(р)
u(t) +
а(р)
f(t).
(2.37)
2.2.
Переходные
процессы
и
характеристики
моделей
вход-выход
59
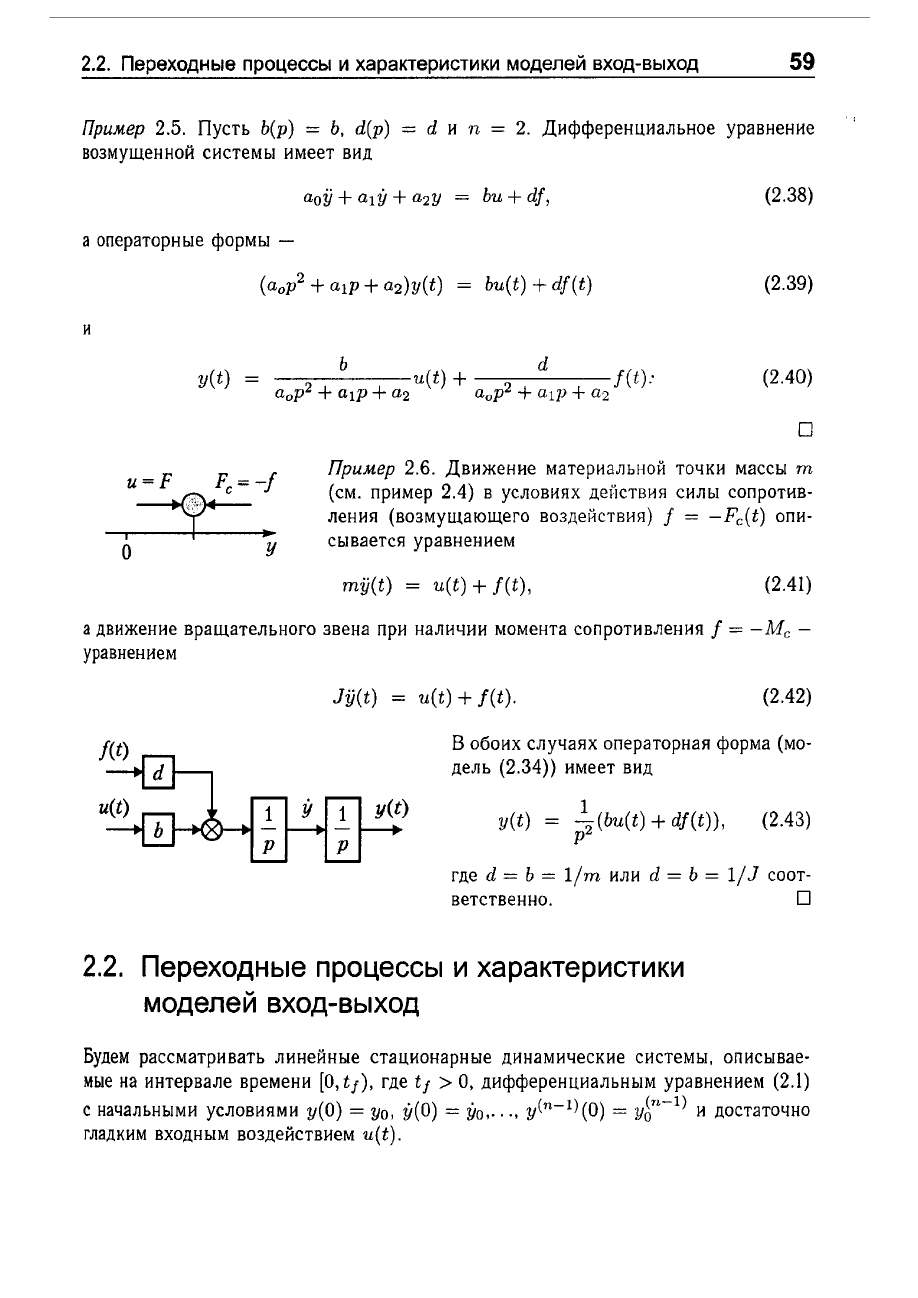
Прuмер
2.5.
Пусть
Ь(р)
=
Ь,
d(p)
= d
и
n =
2.
Дифференциальное
уравнение
возмущенной
системы
имеет
вид
а
операторные
формы
-
и
y(t)
и=Р
рс=-!
~
I
..
О
У
(2.38)
bu(t) + df(t)
(2.39)
(2.40)
о
Прuмер
2.6.
Движение
материальной
точки
массы
m
(см.
пример
2.4)
в
условиях
действия
силы
сопротив
ления
(возмущающего
воздействия)
f =
-Fc(t)
опи
сывается
уравнением
mjj(t) = u(t) +
f(t),
(2.41)
а
движение
вращательного
звена
при
наличии момента
сопротивления
f =
-М
с
-
уравнением
Jjj(t) = u(t) +
f(t).
(2.42)
iJ
1
y(t)
в
обоих
случаях
операторная
форма
(мо
дель
(2.34))
имеет
вид
1
y(t) =
2"
(bu(t) + df(t)),
Р
(2.43)
где
d =
Ь
=
1/т
или
d =
Ь
=
1/
J
соот
ветственно.
О
2.2.
Переходные
процессы
и
характеристики
моделей
вход-выход
Будем
рассматривать
линейные
стационарные
динамические
системы,
описывае
мые
на
интервале
времени
[О,
t
f)'
где
t f >
О,
дифференциальным
уравнением
(2.1)
с
начальными
условиями
у(О)
=
Уа,
У(О)
=
Уа,
.
..
,
y(n-l)
(О)
=
Y6
n
-
1
)
и
достаточно
гладким
входным
воздействием
u(t).
