Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.


100
Глава
З.
Математические
модели
вход-состояние-выход
В
условиях
действия
силы
сопротивления
f
(возмущающего
воздействия,
см.
при
мер
2.6)
уравнение
движения
(модель
ВВ)
принимает
вид
ii
=
Ьu
+ df·
Здесь
модель
ВСВ
находится
как
или
х
I
~ ~
I
х+
I
~
I
и
+ I
~
I
J,
у
11
О
1
х.
3.2.3.
Статический
режим
(3.83)
(3.84)
о
Рассмотрим
поведение
модели
ВСВ
при
постоянном
входном
(управляющем)
воз
действии,
т.
е.
и
==
const.
В
этом
случае
решение
дифференциального
уравне
ния
(3.10),
соответствующее
установившейся
составляющей
переходного
процесса,
ищется
в
виде
х
=
Х
у
==
const.
Замечая,
что
Х
у
=
О,
находим:
о
=
Аху
+Вu.
(3.85)
При
условии,
что
det
А
=1-
о
(т. е.
Лi{А}
=1-
О),
алгебраическое
уравнение
(3.85)
единственным
образом
разрешимо
относительно
Х
у
:
Х
у
=
-А-
1
вu.
(3.86)
Подставляя
найденное
решение
в
уравнение
выхода
(3.51),
находим
статическую
характеристику
системы
(3.10),
(3.51)
(3.87)
Принимая
во
внимание
выражение
(2.75),
с
очевидностью
можно
записать
(3.88)
и
получить
выражение
(2.75).
Если
система
такова,
что
det
А
=
О,
то
матрица
А
необратима,
и
система
не
имеет
статического
режима
(см.
2.2.5).
3.3.
Фазовые
траектории
автономной
системы
второго
порядка
3.3.
Фазовые
траектории
автономной
системы
второго
порядка
Рассмотрим
автономную
систему
второго
порядка:
с
начальными
значениями
Уа,
Уа.
Характеристическое
уравнение
системы
р2
+
а1Р
+
а2
=
О
101
(3.89)
(3.90)
имеет
два
вещественных
или
комплексно-сопряженных
корня
(полюса
системы):
-а1
=F
Jai
-
4а2
Р1,2
= 2 '
(3.91)
расположение
которых
на
комплексной
плоскости
определяет
вид
переходных
про-
цессов
У
= y(t,
Уа,
Уа)
(3.92)
и
динамические
свойства
системы
(см.
1.4.1
и
главу
6).
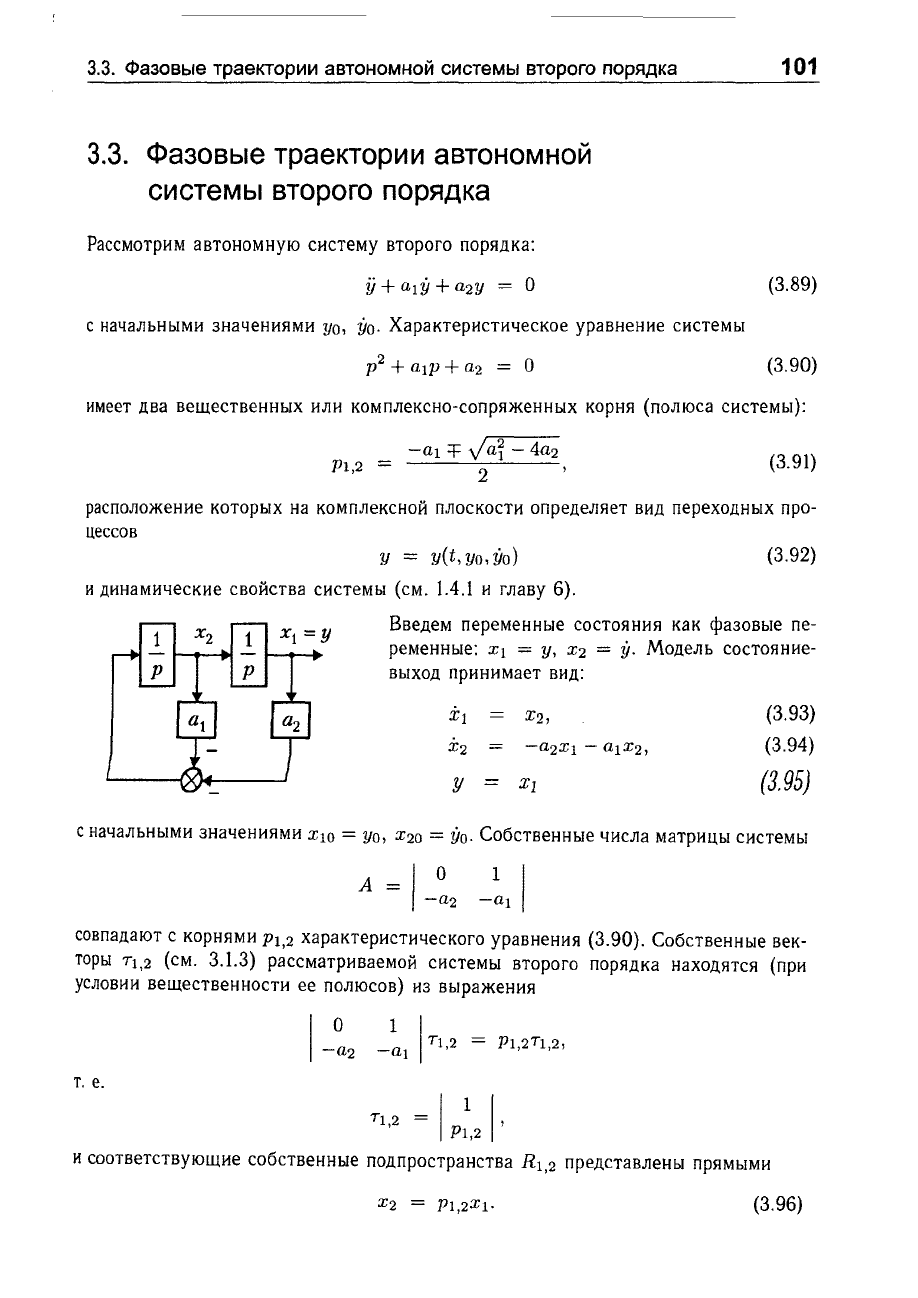
Введем
переменные
состояния
как
фазовые
пе
ременные:
Х1
=
У,
Х2
=
У.
Модель
состояние
выход
принимает
вид:
у
=
Хl
(3.93)
(3.94)
(3.95)
с
начальными
значениями
Х1а
=
Уа,
Х2а
=
Уа.
Собственные
числа
матрицы
системы
совпадают
с
корнями
Р1,2
характеристического
уравнения
(3.90).
Собственные
век
торы
71,2
(см.
3.1.3)
рассматриваемой
системы
второго
порядка
находятся
(при
условии
вещественности
ее
полюсов)
из
выражения
1
о
1
171'2
=
Р1,2
7
1,2,
-а2
-а1
т.
е.
Тl,2
= 1
p~,21
'
и
соответствующие
собственные
подпространства
R
1
,2
представлены
прямыми
(3.96)

102
Глава
З.
Математические
модели
вход-состояние-выход
Равновесные
(установившиеся)
состояния
(xi,
Х2)
системы
(3.93)-(3.95)
находятся
из
условия
(3.97)
При
а2
=J.
о
получаем,
что
единственным
положением
равновесия
является
начало
координат
x~
=
о,
Х2
=
о,
(3.98)
а
при
а2
=
О
находим
множество
равновесных
состояний
(прямую)
Х2
=
О.
(3.99)
Напомним,
что
фазовой
траекторией
(интегральной
кривой)
рассматриваемой
си
стемы
является годограф
вектора
состояния
I
:~~:~
1=1
~Ш
I
при
изменении
пара
метра
t,
а
множество
фазовых
траекторий,
полученных
для
различных
начальных
условий,
образуют
ее
фазовый
портрет
(см.
3.1.2).
Фазовые
траектории
могут
быть
получены
экспериментально
или
найдены
аналитическим
путем.
В
послед
нем
случае
используется
следующий
прием.
Уравнения
(3.93)-(3.94)
записываются
в
виде
dXl
X2
dt
,
dX2
-(а2Хl
+
al
X
2)dt.
После
деления
второго
выражения
на
первое
получаем
дифференциальное
уравне-
ние
dX2
dXl
Решение
этого
уравнения
ищется
в
виде
(3.100)
(3.101)
и
определяет
интегральную
(фазовую)
траекторию
рассматриваемой
системы
на
плоскости
}R2.
Рассмотрим
переходные
процессы,
соответствующие
различным
значениям
корней
характеристического
уравнения
(полюсов
системы
(3.93)-(3.94)).
1.
Для
неравных
вещественных
полюсов
(рис.
3.4)
Рl,2
=
Йl,2
(3.102)
уравнение
(3.89)
имеет
решение
(3.103)
что
соответствует
апериодическому
процессу
(см.
2.2.2).
3.3.
Фазовые
траектории
автономной
системы
второго
порядка
103
б~m
Р2
Рl
а
О
Re
а
1т
Р2
Рl
Рис.
3.4
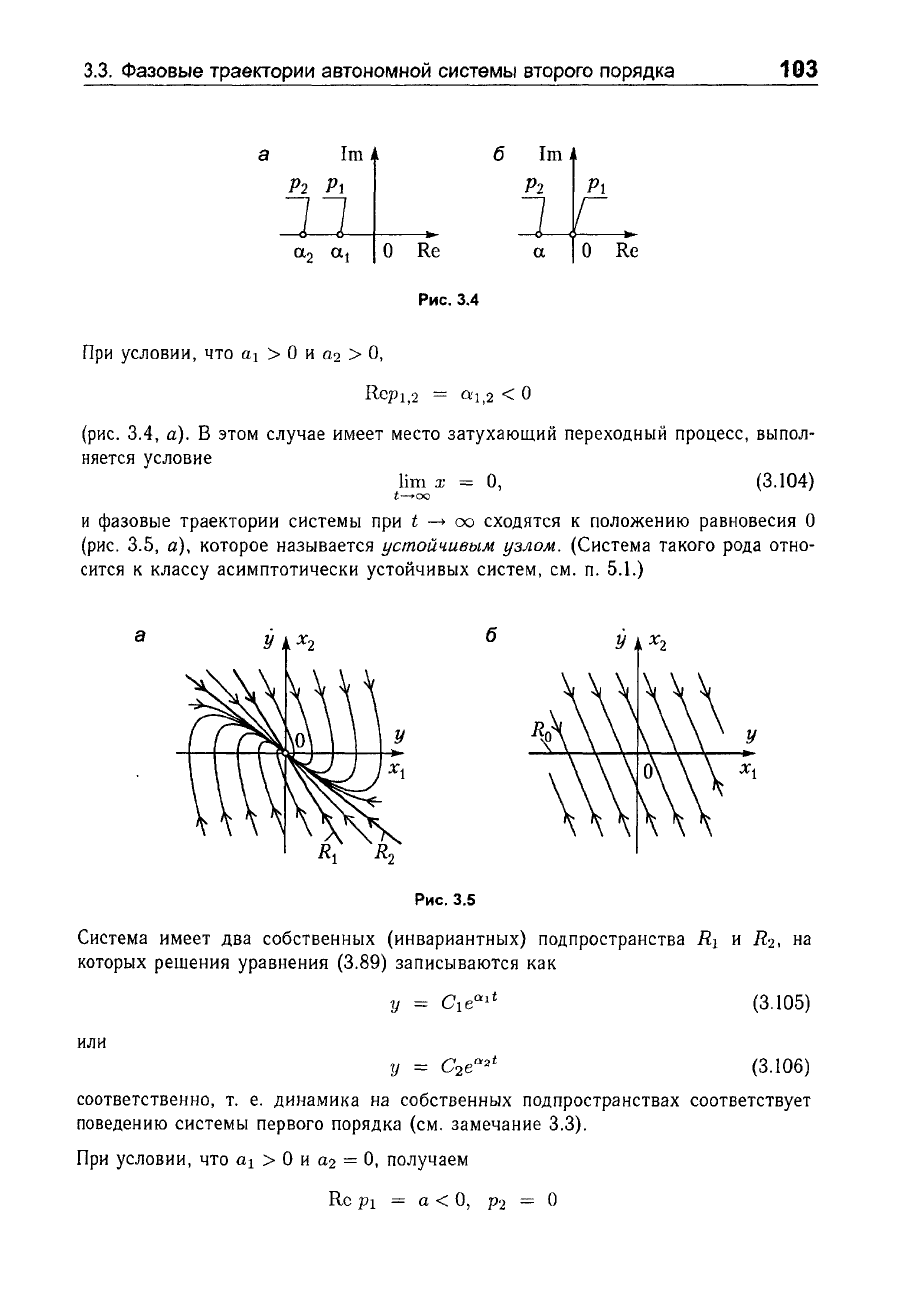
При
условии,
что
аl
>
О
и
а2
>
О,
RCPl,2
= 0:1,2 <
О
(рис.
3.4,
а).
В
этом
случае
имеет
место
затухающий
переходный
процесс,
выпол-
няется
условие
Нт
х
=
О,
t-oo
(3.104)
и
фазовые
траектории
системы
при
t
~
00
сходятся
к
положению
равновесия
О
(рис.
3.5,
а),
которое
называется
устойчивым
узлом.
(Система
такого
рода
отно
сится
к
классу
асимптотически
устойчивых
систем,
см.
п.
5.1.)
а
б
у
Рис.
3.5
Система
имеет
два
собственных
(инвариантных)
подпространства
R
1
и
R
2
,
на
которых
решения
уравнения
(3.89)
записываются
как
(3.105)
или
(3.106)
соответственно,
т.
е.
динамика
на
собственных
подпространствах
соответствует
поведению
системы
первого
порядка
(см.
замечание
3.3).
При
условии,
что
al
>
О
И
а2
=
О,
получаем
Rc
Рl
=
а
<
О,
Р2
О
104
Глава
З.
Математические
модели
вход-состояние-выход
(рис.
3.4,
б).
Фазовые
траектории
системы
(рис.
3.5,
б)
при
t
-4
00
сходятся
К
мно
жеству
равновесных
состояний
(прямой
R
o
),
описываемому
уравнением
(3.99).
Это
же
множество
является
собственным
подпространством
системы.
(Система
такого
рода
относится
к
классу
устойчивых
по
Ляпунову,
или
нейтрально
устойчивых,
систем,
см.
п.
5.1.)
а
1т
б
1т
Р2
Рис.
З.6
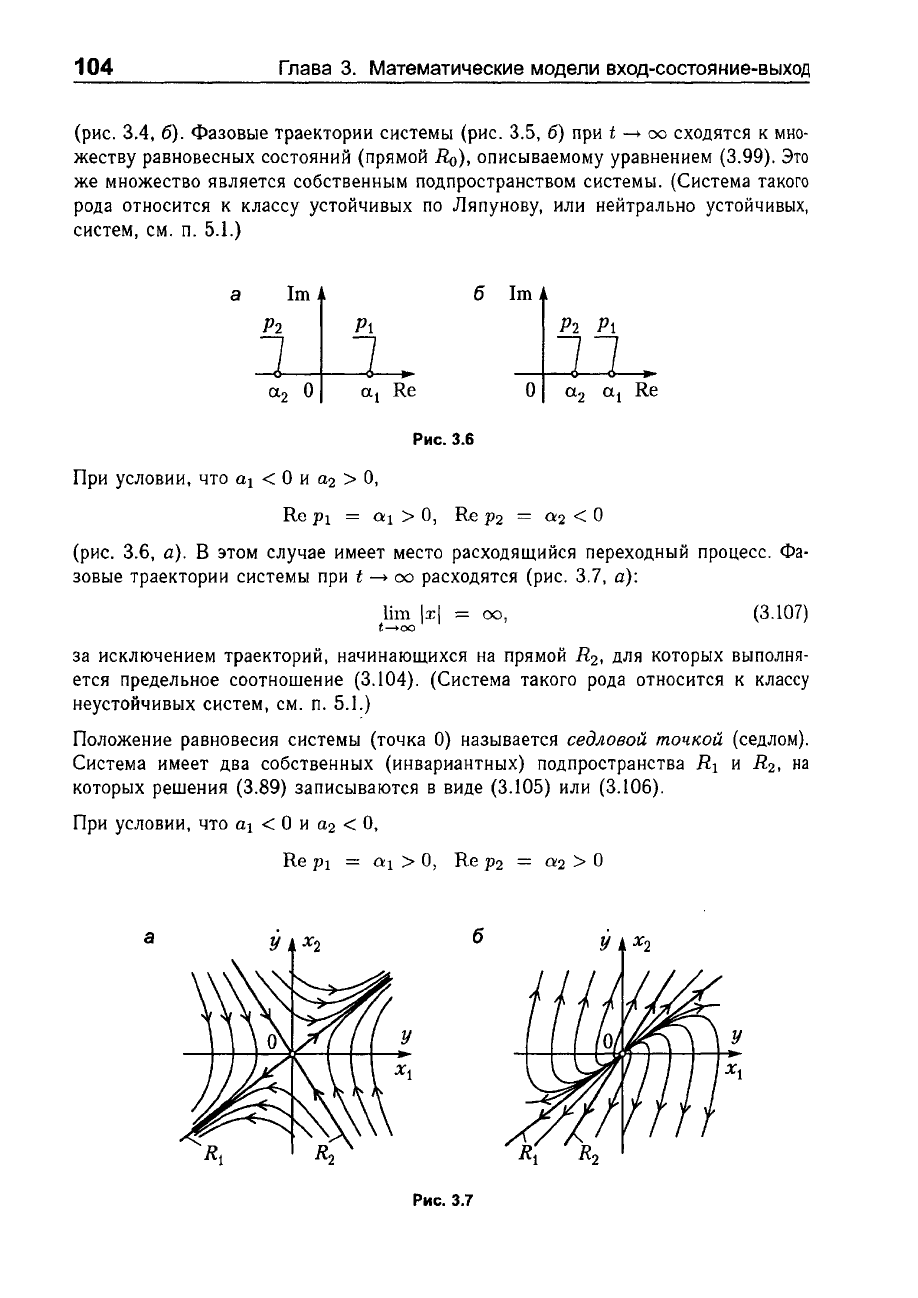
При
условии,
что
аl
<
О
и
а2
>
О,
Re
Рl
=
аl
>
О,
Re
Р2
=
а2
<
О
(рис.
3.6,
а).
В
этом
случае
имеет
место
расходящийся
переходный
процесс.
Фа
зовые
траектории
системы
при
t
-4
00
расходятся
(рис.
3.7,
а):
lim
Ixl
=
00,
t-oo
(3.107)
за
исключением
траекторий,
начинающихся
на
прямой
R
2
,
дЛЯ
которых
выполня
ется
предельное
соотношение
(3.104).
(Система
такого
рода
относится
к
классу
неустойчивых
систем,
см.
п.
5.1)
Положение
равновесия
системы
(точка
О)
называется
седловой
точкой
(седлом).
Система
имеет
два
собственных
(инвариантных)
подпространства
R
1
и
R
2
,
на
которых
решения
(3.89)
записываются
в
виде
(3.105)
или
(3.106).
При
условии,
что
аl
<
О и а2
<
О,
Re
Рl
=
аl
>
О,
Re
Р2
а
б
Рис.
З.7

3.3.
Фазовые
траектории
автономной
системы
второго
порядка
105
(рис.
3.6,
б).
В
этом
случае
имеет
место
расходящийся
переходный
процесс
и
все
фазовые
траектории
(рис.
3.7,
б)
системы
при
t
-+
00
расходятся
(выполняет
ся
(3.107».
Положение
равновесия
системы
(точка
О)
называется
неустойчuвым
узлом
(и
система
неустоЙчива).
Система
также
имеет
два
собственных
(инвари
антных)
подпространства
R
1
и
R
2
.
2.
Если
а2
=
ar/4,
то
система
имеет
равные
вещественные
полюсы
(рис.
3.8)
аl
Рl,2
=
а
=
-2'
и
решение
уравнения
(3.89)
принимает
вид:
соответствующее
апериодическому
процессу
(см.
2.2.2).
а
1т
б
IJ;
Рl,2
Рl,2
аО
Re
О
Re
в
Рис.
3.8
При
условии,
что
а2
>
О
(и
аl
>
О),
Re
Рl,2
=
а
<
О
1
A
Рl,2
О
а
Re
(рис.
3.8,
а).
В
этом
случае
имеет
место
затухающий
переходный
процесс,
выпол
няется
предельное
соотношение
(3.104),
фазовые
траектории
при
t
-+
00
сходятся
к
положению
равновесия
(устойчивому
узлу)
О
(рис.
3.9,
а),
и
система
асимпто
тически
устойчива.
Собственные
подпространства
системы
R
1
и
R
2
совпадают.
При
условии,
что
аl
=
а2
=
О,
получаем
Рl
=
Р2
=
О
.
(рис.
3.8,
б)
и
расходящийся
переходный
процесс.
Фазовые
траектории
системы
(рис.
3.9,
б)
при
t
-+
00
уходят
в
бесконечность,
за
исключением
траекторий,
начинающихся
на
множестве
равновесных
состояний
(прямой
R
o
),
описываемом
уравнением
Х2
= const,
и
система
неустоЙчива.
При
условии,
что
а2
<
О
и
аl
<
О,
выполняется
Re
Рl,2
=
а>
О
106
Глава
З.
Математические
модели
ВХОД-СО9ТQЯJiИе",QbIХОД
а
б
у
Х
2
в
...
....
,. ,.
~
....
~
.....
,.
,
"
у
....
у
,.
,.
-R;
{)
.;
Х'1
~
;;,
- -
.,
"' "'
.1'
.1'
~
~
Рис.
3.9
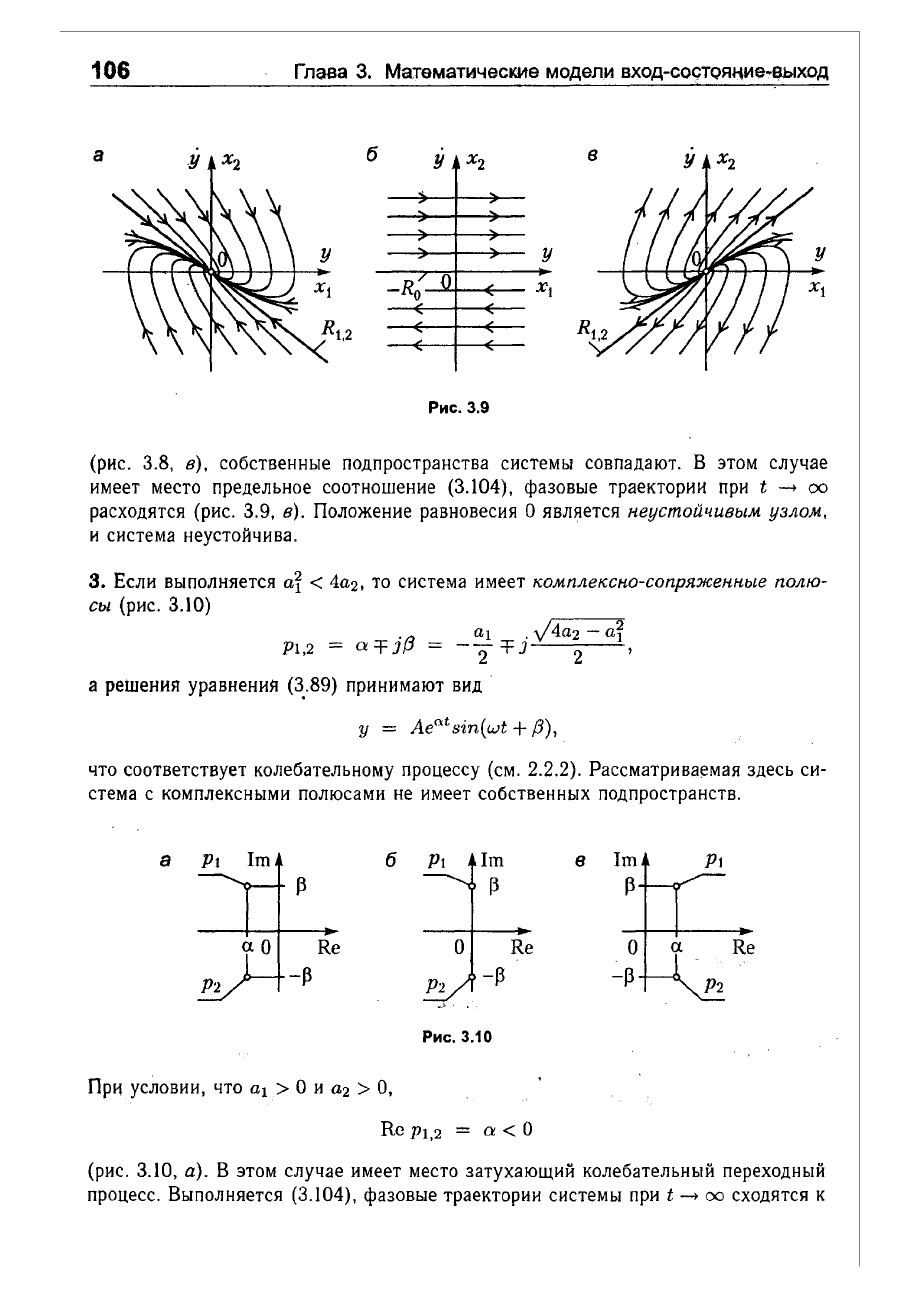
(рис.
3.8,
В),
собственные
подпространства
системы
совпадают.
В
этом
случае
имеет
место
предельное
соотношение
(3.104),
фазовые
траектории
при
t
-+
00
расходятся
(рис.
3.9,
В).
Положение
равновесия
О
является
неусmойчuвым
узлом,
и
система
неустоЙчива.
3.
Если
выполняется
ау
<
4а2,
то
система
имеет
комплексно-сопряженные
полю
сы
(рис.
3.1
О)
.
аl.
v4a2
-
ау
Рl,2
=
а
=f
J
f3
=
-"2
=f
J 2 '
а
реШения
уравнений
(~.89)
принимают
вид'
у
=
Аеаtsin(wt+/З),
что
соответствует
колебательному
процессу
(см.
2.2.2).
Рассматриваемая
здесь
си
стема
с
комплексными
полюсами
не
имеет
собственных
подпространств.
а
Рl
1т
б
Рl
1т
в
1т
РI
~
~
а.
О
Re
Re
о
а.
Re
-~
-13
-13
Рис.
3.10
ПРI1
условии,
что
аl
>
О
И а2
>
О,
Rc
PI,2
=
а
<
О
(рис.
3.10,
а).
В
этом
случае
имеет
место
затухающий
колебательный
переходный
процесс.
Выполняется
(3.104),
фазовые
траектории
системы
при
t
-+
00
сходятся
к

3.4.
Эквивалентные
преобразования
и
канонические
представления
107
а
б
у
Х
2
в
у
Рис.
3.11
положению
равновесия
О
(рис.
3.11,
а),
которое
называется
устойчивым
фокусом,
и
система
асимптотически
устойчива.
При
условии,
что
а2
=
О,
Rc
Рl,2
=
О,
система
имеет
чисто
мнимые
корни
Рl,2
=
-jj3
(рис.
3.10,
б)
и
является
линейным
осциллятором
(см.
п.
2.3
и
пример
2.6).
В
этом
случае
имеет
место
незатухающий
колебательный
процесс.
Фазовые
траектории
системы
представлены
замкнутыми
концентрическими
кривыми
(эллиптическими
орбитами),
и
система
(нейтрально)
устойчива
(рис.
3.11,
б).
Положение
равновесия
системы
(точка
О)
называется
центром.
При
условии,
что
аl
<
О
И
а2
<
О,
Rc
Pl,2
=
а>
О
(рис.
3.10,
в).
В
этом
случае
имеет
место
расходящийся
колебательный
переход
ный
процесс.
Фазовые
траектории
системы
при
t
-t
00
расходятся
от
положения
равновесия
О
(рис.
3.11,
в),
которое
называется
неусmойчивым
фокусом,
и
система
неустоЙчива.
3.4.
Эквивалентные
преобразования
и
канонические
представления
Как
отмечалось
в
подразделе
3.1.1,
возможны
различные
способы
выбора
перемен
ных
состояния
динамической
системы.
Неоднозначность
такого
выбора
определяет
неединственность
моделей
вход-состояние-выход
(3.48)-(3.49)
(или
(3.50)-(3.51»,
соответствующих
конкретной
модели
вход-выход
(2.1),
(2.3)
или
(2.8),
так
как
выбор
иных
переменных
состояния
приводит
к
получению
другой
модели
вев.
е
другой
стороны,
первоначальная
модель
вев
может
быть
специально
преобра
зована,
что
обычно
связывают
с
изменением
базиса
(системы
координат)
простран-

108
Глава
3.
Математические
модели
вход-состояние-выход
ства
состояний
jRn.
Такого
рода
преобразование
называется
эквивалентным,
или
nреобразованием
подобия
[2,
3,
9,
20,
21].
3.4.1.
Эквивалентные
преобразования
Рассмотрим
одноканальную
систему
(объект
управления),
модель
вход-выход
ко
торой
задается
операторным
уравнением
где
a(p)y(t) = b(p)u(t),
а(р)
=
рn
+
alpn-l
+
...
+
an-lР
+
а
n
,
Ь(р)
=
b1pn-l
+
...
+
Ь
n
-
1
Р
+
Ь
n
,
(3.108)
и
Pi
-
корни
характеристического
уравнения
(полюсы
системы),
или
уравнением
(2.8),
где
а(р)
W(p) =
Ь(р)'
(3.109)
Модель
ВСБ
рассматриваемой
системы
может
быть
записана
в
форме
(3.50)-(3.51).
Введем
в
рассмотрение
новый
(преобразованный)
вектор
состояния:
х*
=
Рх,
(3.110)
где
Р
-
матрица
nреобразования
(подобия),
удовлетворяющая
условию
det
Р
=1=
=1=
О.
Тогда
существует
обратное
преобразование
х
=
p-1x*.
Дифференцируя
по
времени
(3.110)
и
подставляя
(3.111),
(3.50)
находим:
х*
=
р
AP-1x*
+
РВи,
и из
выражения
(3.51)
-
у
=
ср-l
х
*.
Полученные
выражения
перепишем
в
виде
где
х*
=
А*х*
+
В*u"
у
=
С*х*,
А*
=
PAp-l
-
матрица,
подобная
матрице
А,
В*
=
РВ,
С*
cp-l,
(3.111)
(3.112)
(3.113)
(3.114)
(3.115)
(3.116)
(3.117)
(3.118)

3.4.
Эквивалентные
преобразования
и
канонические
представления
109
Подобные
матрицы
обладают
следующими
свойствами.
Свойство
3.6.
dеt(лl
-
А)
=
dеt(лl
-
А*)
=
а(Л).
Свойство
3.7.
Модель
(3.114), (3.115)
называется
эквивалентной
(подобной)
модели
(3.50)-
(3.51).
Справедливо
также
очевидное
свойство.
Свойство
3.8.
W(p)
(3.119)
Таким
образом,
для
подобных
систем
сохраняются
связи
выходных
и
входных
переменных,
и
следовательно,
им
соответствуют
общие
модели
ВВ
(2.1),
(2.3),
(2.8).
3.4.2.
Канонические
представления
моделей
ВСВ
Наиболее
простые
модели
вход-состояние-выход,
соответствующие
исходным
урав
нениям
системы
(3.50)-(3.51),
называются
каноническими
представлениями
(формами).
Диагональной
формой
называется
модель
(рис.
3.12),
представленная
уравнениями
состояния
Х1
=
Л1
Х
1
+
fЗ1
и,
Х2
Л2
Х
2
+
/32
и
,
(3.120)
и
уравнением
выхода
у
=
Х1
+
Х2
+
...
+
Х
n
·
(3.121)
Модель
может
быть
записана
в
компактной
форме
(3.114)-(3.115),
где
Л1
О
О
/31
О
Л2
О
/32
А*
=
Л
=
,
В*
=
,
С*
I 1
1
" .
1
1.
о
о
л
m
(3n
