Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.

90
Глава
З.
Математические
модели
вход-состояние-выход
Здесь
J -
жорданова
матрица:
J
1
О
О
О
J
2
О
J
=
diag{ J
i
}
=
О О
J
i
диагональные
элементы
которой
J
i
для
случая
кратных
собственных
чисел
Лi
представлены
матрицами
вида
.Ai
1
О
О
О
.Ai
1
О
О
О
О
1
О О О
.Ai
а
для
пары
комплексно-сопряженных
чисел
.Ai,i+1 =
ai
±
j{3i
-
матрицами
~атричная
функция
At
1 2 2 1 i i
exp(At) =
е
=
I+At+
2
!At
+
...
+пАt
+...
(3.31)
называется
матричной
экспонентой.
~атричная
экспонента
диагональной
матри
цы
Л
рассчитывается
по
простой
формуле
е
Л1t
О
О
е
лt
О
е
Л2t
О
О
О
е
Лпt
в
более
общем
случае
(для
случая
некратных
вещественных
корней)
из
выражения
(3.29)
получаем:
А
=
ТЛТ-I,
(3.32)
и
используя
определение
матричной
экспоненты
(3.31),
выводим
следующее
поло
жение.
Свойство
3.2.
(3.33)
Найдем
собственные
числа
Zi
матрицы
e
Al
,
т.
е.
корни
характеристического
урав-,
нения
det(zI
- e
At
) =
о.

3.1.
Понятие
пространства
состояний
и
модели
состояние-выход
91
Принимая
во
внимание
выражение
(3.33),
получаем
(3.34)
Так
как
dct(zI
-
е
Лt
)
=
Пf(z
-
е
Лit
),
то
из
выражения
(3.34)
следует,
что
искомые
собственные
числа
Zi
удовлетворяют
уравнению
п
п(z
-
ел,t)
=
О,
i=1
откуда
вытекает
следующее
положение.
Свойство
3.3.
(3.35)
Учитывая
свойство
3.2,
нетрудно
получить
решения
системы
уравнений
(3.10)-
(3.11).
Сначала
перепишем
формулу
для
расчета
вектора
состояния
(3.17)
в
виде
x(t)
=
Те
Лt
Т-
1х
о
=
=
I
71
72
" .
7
n
I
Учитывая,
что
Т-
1
Т
=
1,
запишем
т
т1
7
1
тТ
7
2
mr
7
1
mr
7
2
т~71
т~72
и,
следовательно,
Тогда
уравнение
(3.36)
принимает
вид
n
е
Л1
О
О
е
Л2
О О
тnТ
т,n
mr7
n
т~т,n
при
i =
j,
при
i
=1=
j.
x(t) =
I::
тТ
хоеЛit7i'
i=1
Введем
обозначения
О
т
Т
1
О
тn
Т
2
(3.36)
Хо·
еЛ"
m~
1,
(3.37)
(3.38)

92
Глава
3.
Математические
модели
вход-состояние-выход
и
получим
решение
системы
(З.10)
в
виде
разложения
по
собственным
векторам:
n n
(З.З9)
i=l
i=l
Здесь
векторы
xi(t)
при
надлежат
собственным
подпространс~вам
R
i
и
называются
собственными
составляющими
решения
x(t),
или
модами
вектора
состояния
системы.
Замечание
З.З.
Если
начальное
значение
вектора
состояния
(для
рассматриваемого
случая
вещественных
некратных
собственных
чисел)
принадлежит
собственному
подпространству
R
j
,
т.
е.
хо
=
Лj7j,
то
(
)
_ \
Т
_
{Л
j
при
i =
j,
J.1i
ХО
-
Лjm
i
7j
-
О
.
-'-
.
при
1,/
J
(З.40)
и,
следовательно,
решение
описывается
простым
выражением
x(t) =
Лjе
Лjt
7j
=
еЛjtХQ.
(З.41)
Последнее
показывает,
что
траектории
многомерной
динамической
системы
(З.10)
целиком
лежат
в
одномерном
собственном
подпространстве
(прямой)
R
j
,
и ее
пове
дение
соответствует
динамике
системы
первого
порядка.
Такого
рода
подпростран
ства
пространства
состояний
IRn
относятся
к
классу
инвариантных
множеств
системы
[26,
27,
зо,
Зl,
45].
Теперь
проанализируем
поведение
выходной
переменной
y(t).
Подставляя
уравне
ние
(З.З9)
в
(З.11),
находим:
n
n
(З.42)
i=l
i=l
где
Yi(t) -
моды
выходной
переменной.
Сравнивая
последнее
уравнение
с
выраже
нием
(2.46),
получаем,
что
неопределенные
коэффициенты
C
i
могут
быть
рассчи
таны
как
(З.43)
Более
того,
имеет
место
важное
положение.
Свойство
3.4.
Полюсы
системы
Pi
совпадают
с
собственными
числами
матрицы
системы
А,
т.
е.
(З.44)
Последний
результат
показывает,
что
характеристические
полиномы
(2.6)
и
(З.25)
также
совпадают,
т.
е.
справедливо
следующее.
Свойство
3.5.
а(л)
dеt(лI
-
А).
(З.45)

3.2.
Модели
управляемых
систем
93
3.2.
Модели
управляемых
систем
Связь
между
входным
воздействием
динамической
системы
и
ее
выходной
пе
ременной
неоднозначна,
т.
е.
одному
и
тому
же
входному
сигналу
u(t)
может
соответствовать
множество
выходных
сигналов
y(t)
(см.
п.
2.2).
Введение
в
рас
смотрение
переменных
состояния
Xi
позволяет
устранить
указанную
неоднознач
насть
-
выход
системы
в
произвольный
момент
времени
tl
~
t
o
единственным
образом
определяется
начальными
значениями
переменных
состояния
XiO
И
задан
ным
на
интервале
времени
[to,
tl]
входным
воздействием
u = U[to,tlJ:
(3.46)
3.2.1.
Модели
вход-состояние-выход
Сначала
рассмотрим
частный
случай
управляемой
ди
намической
системы
с
одним
входом
u(t)
и
одним
вы
ходом
y(t),
описываемой
уравнением
(2.10),
где
ао
=
1.
Введем
в
рассмотрение
переменные
состояния
(3.3).
Дифференцируя
(3.3)
по
времени
и
подставляя
(2.10),
находим
уравнения
состоя-
ния:
(3.4
7)
При
этом
уравнение
выхода
по-прежнему
имеет
вид
(3.6).
Уравнения
(3.47)
и
(3.6)
представляют
собой
простейший
случай модели
вход-состояние-выход
(ВСВ).
В
более
общем
случае
модель
ВСВ
управляемой
динамической
системы
(2.1)
со
держит
уравнения
состояния
вида
а11Хl
+
а12Х2
+ ... +
аlnХn
+
Ь
1
и,
а21
Хl
+
а22
Х
2
+ ... +
а2nХn
+
Ь
2
и,
(3.48)
и
уравнение
выхода
(3.49)
где
aij,
b
i
,
Ci
-
вещественные
коэффициенты
(параметры).
Для
преобразования
к
kомпактной
векторно-матричной
форме
необходимо
определить
вектор
состояния

94
Глава
3.
Математические
модели
вход-состо~ни~-выход
Х
= {Xi}'
1,n,
матрицы
А
= {aij},
0=
{Ci},
а
также
матрицу
размера
n
Х
1
Ь
1
В
{b
i
}
Ь
2
=
Ь
N
Тогда
уравнения
(3.48)-(3.49),
описывающие
модель
вход-состояние-выход,
при
нимают
вид:
х
-
Ах+Ви,
у
=
Сх,
(3.50)
(3.51)
где
Х(О)
=
Хо.
Модель
(3.50)-(3.51)
связывает
вход
u(t)
и
выход
y(t)
через
вектор
промежуточных
переменных
Xi(t).
в
частном
случае,
когда
модель
вев
представлена
в
форме
(3.47), (3.6),
получаем
матрицы
О
1
О
О
О
О
О
1
О
О
А
=
,
в
=
о
о
о
1
О
-а
n
-an-l
-а
n
-2
-al
Ь
0=11
О
...
о
о
1.
Аналогично
находится
модель
вев
многоканальной
(многосвязной)
системы
(см.
модель
(2.30».
в
общем
случае
она
содержит
уравнения
состояния
вида
аll
Х
l
+ ... +
аln
Х
n
+
ы
l
иl
+ ... +
Ь
1rn
,и
rn
"
а21
Х
l
+ ... +
а2n
Х
n
+
Ь
21
иl
+ ... +
Ь
2rn
,и
rn
"
(3.52)
и
уравнения
выходов
(3.22).
Определим
1n'-мерный
вектор
управления
и
=
{Щ},
j =
1,
т',
и
т-мерный
вектор
выходов
у
= {Yj}, j =
1,
т,
а
также
матрицы
размера
n
Х
т'
и
т
Х
n
соответственно.
Тогда
уравнения
(3.52)
и
(3.22)
можнq
переписать
в
виде
(3.50)
и
(3.51).

3.2.
Модели
управляемых
систем
95
Рассмотрим
возмущенную
динамическую
систему,
(см.
модель
(2.32)),
т.
е.
управляемую
систему,
на
вход
которой
дополнительно
действует
входной
сигнал
(воз
мущающее
воздействие)
f(t).
Уравнение
состояния
та-
кой
системы
записывается
в
виде:
а11
Х
l
+
а12
Х
2
+
...
+
аlп
Х
п
+
Ь
1
и
+ d
1
j,
а21Хl
+
а22
Х
2
+ ... +
а2пХп
+
Ь
2
и
+ d
2
j,
(3.53)
где
d
i
(i =
1,
n) -
коэффициенты,
а
уравнение
выхода
сохраняет
форму
(3.49).
Векторно-матричная
форма
модели
(3.53), (3.49)
имеет
вид:
где
D = {d
i
},
i = 1,n.
х
-
Ax+Bu+Dj,
у
=
Ох,
(3.54)
(3.55)
Если
на
вход
системы
действует
несколько
возмущающих
воздействий
fj,
j =
1,
k,
то
в
уравнении
(3.54) f =
{jj}
-
вектор
возмущений,
а
D = {Dij}.
В
частном
случае, когда
модель
ВВ
имеет
вид
-(2.35),
уравнения
состояния
возму
щенной
системы
принимают
вид
а
в
уравнении
(3.54) -
D =
о
о
d
(3.56)
Рассмотрим
решения
уравнений
(3.50), (3.51),
полагая
to
=
О.
Решение
уравнения
состояния
(3.50)
можно
представить
в
виде:
x(t) =
х"
+
х,
=
еА'хо
+
l'
eA('-т)
BU(T)dT, (3.57)
где
XCB(t)
-
свободная
составляющая
(переходный
процесс
автономной
системы),
~оответствующая
решениям
однородного
дифференциального
уравнения
(3.10)
и
зависящая
от
начальных
условий
Хо,
xB(t)
-
вынужденная
составляющая,
соот
ветствующая
переходному
процессу
системы
(3.50)
при
нулевых
начальных
усло
виях
ХО
=
О
(реакция
системы
на
входное
воздействие
u(t)).
Подставляя
(3.57)

96
Глава
З.
Математические
модели
вход-состояние-выход
в
уравнение
выхода
(3.51),
получаем
y(t) =
Уев
+
Ув
=
CeAtxo
+ r
t
CeA(t-r)
Bu(r)dr.
(3.58)
./0
Отметим,
что
матрица
(3.59)
является
весовой
(импульсной
переходной)
матрицей
(при
m =
т'
= 1 -
весовой
функцией),
и,
следовательно,
уравнение
У,
=
/.'
CeA('-т)
Bu(r)dr
(3.60)
совпадает
с
приведенным
ранее
выражением
(2.62).
Для
возмущенных
моделей
ВСВ
решения
могут
быть
получены
в
аналогичной
форме.
3.2.2.
Передаточная
функция
(матрица)
и
структурные
схемы
моделей
ВСВ
Приведенные
выше
уравнения,
описывающие
модели
вход-состояние-выход,
могут
быть
записаны
в
операторной
форме
(см.
п.
2.1).
Рассмотрим
уравнения
(3.50)-
(3.51).
Используя
оператор
дифференцирования
р
=
d/dt,
запишем
х
=
р
х.
Тогда
из
уравнения
состояния
(3.50)
после
простейших
алгебраических
преобразований
находим
х
=
(рl
-
A)-l
Вu.
Подставляя
последнее
выражение
в
уравнение
выхода
(3.51),
получаем
Введем
обозначение
W(p)
и
запишем
уравнение
(3.62)
в
виде
С(рl
-
A)-lВ
У
=
W(p)u.
(3.61)
(3.62)
(3.63)
(3.64)
Сравнение
с
уравнением
(2.31)
показывает,
что
матричный
интегро·
дифференциальный
оператор
W(p)
есть не
что
иное,
как
передаточная
матрица
управляемой
динамической
системы
(см.
п.
2.1.3).
Рассмотрим
свойства
оператора
(3.63).
Матрица
(рl
-
А)-l,
называемая
резоль
вентой,
может
быть
представлена
в
виде
[2,
9]:
(рl
_
A)-l
=
adj(pl
-
А)
det(pl
-
А)
pn-l
+ R
1p
n-2
+ ... + R
n
dct(pl
-
А)
(3.65)
3.2.
;Модели
управляемых
систем
97
где
R
i
-
числовые
матрицы
n
х
n.
Тогда
W(p)
=
B1pn-l
+ ... +
В
n
det(pI -
А)
В(р)
(3.66)
det(pI -
А)'
где
B
i
=
ORiB;
В(р)
-
матричный
оператор.
Для
случая
одноканальной
системы
(т
=
т'
=
1)
W(p)
-
передаточная
функция.
Сравнивая
(3.65)
с
выражением
(2.9),
найдем,
что
dct(pI -
А)
=
а(р)
(3.67)
-
характеристический
полином
системы
(см.
также
свойство
3.5);
а
В(р)
=
Ь(р)
-
характеристический
полином
правой
части
дифференциального
уравнения
(2.1).
Из
(3.67)
следует
свойство
3.4 -
собственные
числа
матрицы
А
В,точности
совпадают
с
корнями
характеристического
уравнения
(полюсами)
системы:
Лi{А}
= Pi.
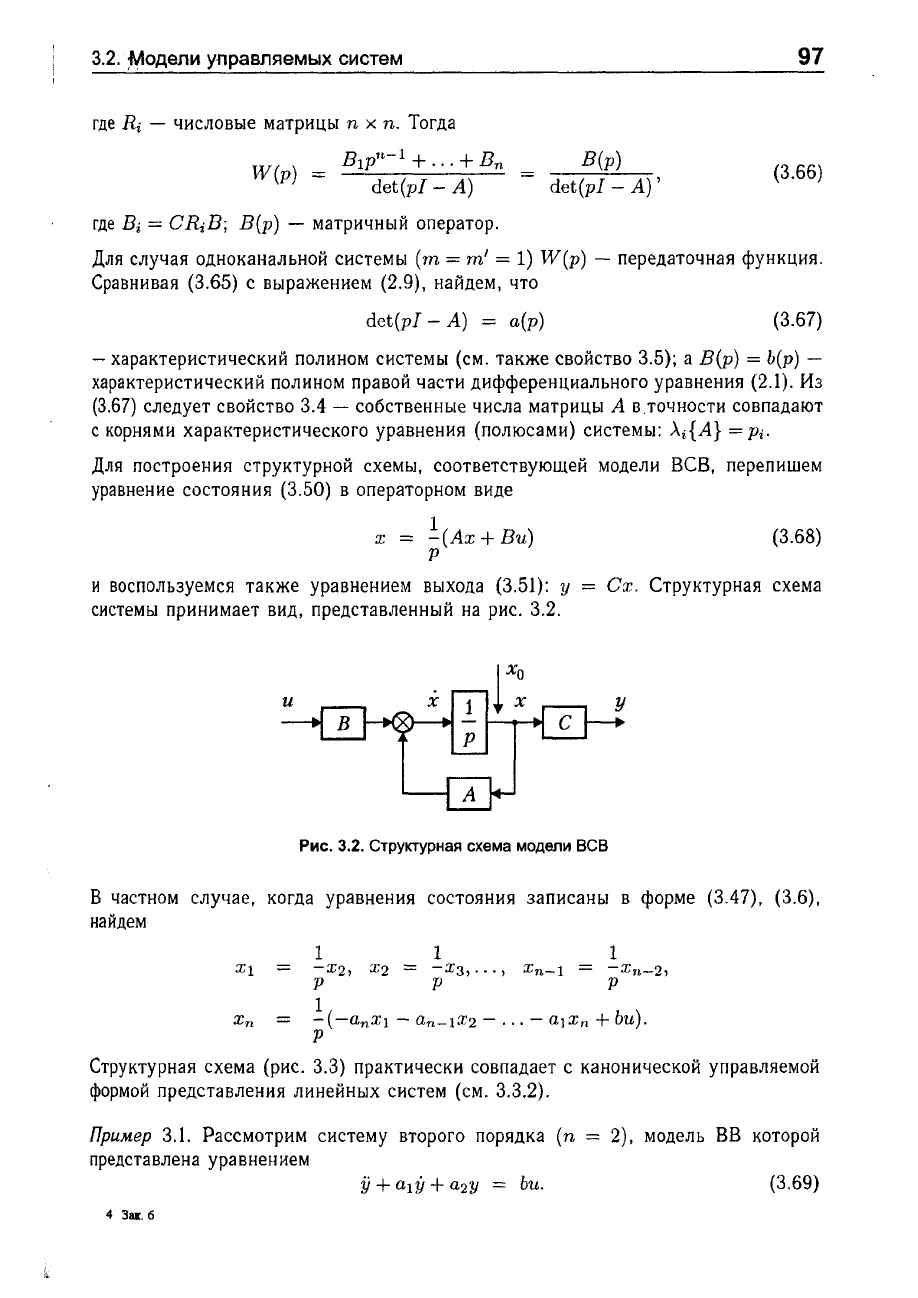
Для
построения
структурной
схемы,
соответствующей
модели
ВСВ,
перепишем
уравнение
состояния
(3.50)
в
операторном
виде
1
х
=
-(Ах+Вu)
р
(3.68)
и
воспользуемся
также
уравнением
выхода
(3.51):
у
системы
принимает
вид,
представленный
на
рис.
3.2.
Ох. Структурная
схема
Рис.
3.2.
Структурная
схема
модели
ВСВ
в
частном
случае, когда
уравнения
состояния
записаны
в
форме
(3.47), (3.6),
найдем
1 1 1
хl
=
-Х2,
Х2
=
-хз,···,
xn-l
=
-Х
n
-2,
р
р
р
1
х
n
= -(
-аnХl
-
a
n
-lХ2
-
...
-
аlХn
+
Ьu).
р
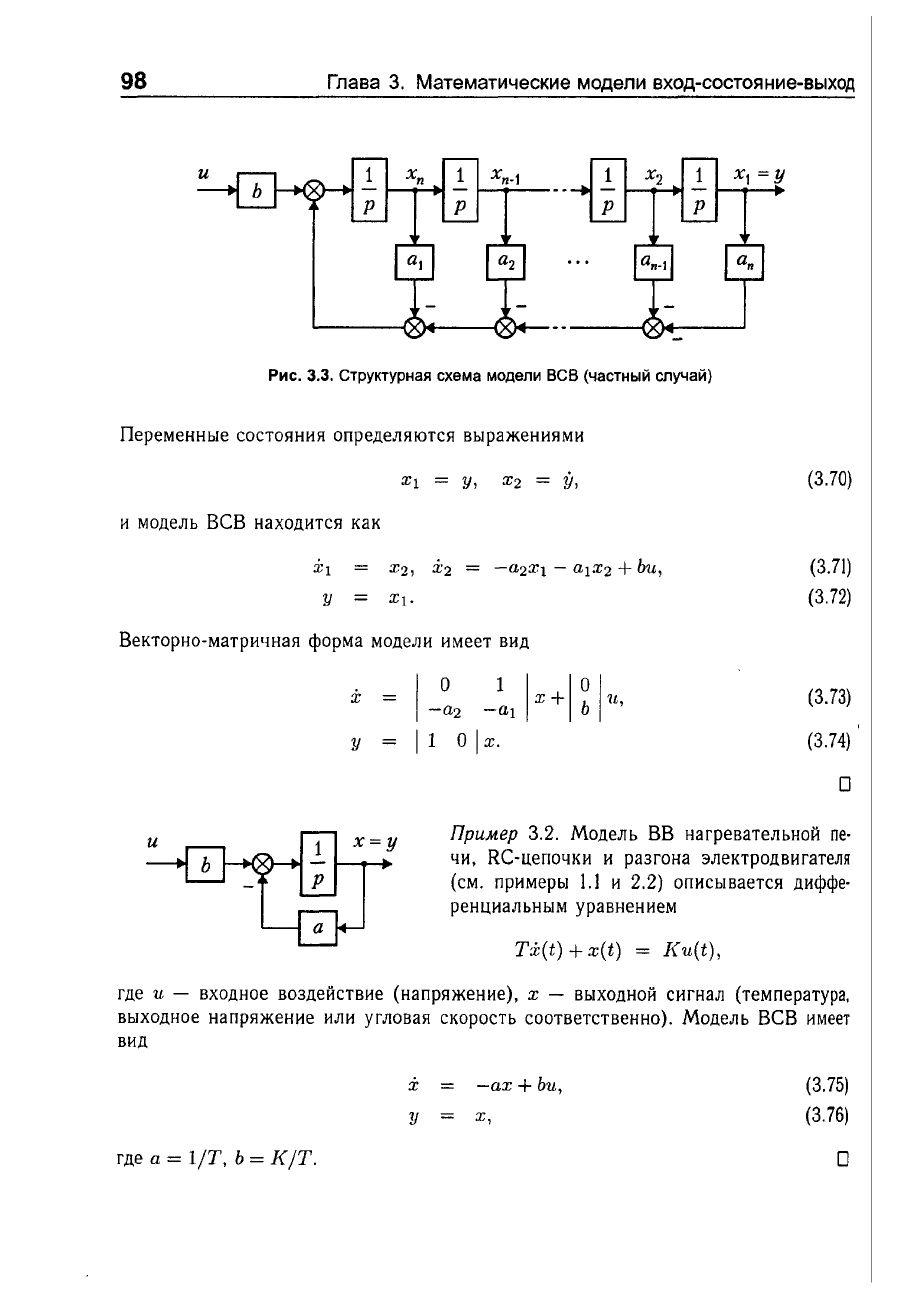
Структурная
схема
(рис.
3.3)
практически
совпадает
с
канонической
управляемой
формой
представления
линейных
систем
(см.
3.3.2).
Прuм,ер
3.1.
Рассмотрим
систему
второго
порядка
(n = 2),
модель
ВВ
которой
представлена
уравнением
(3.69)
4
ЗU:.6
98
Глава
З.
Математические
модели
вход-состояние-выход
р р
р
Рис.
3.3.
Структурная
схема
модели
ВСВ
(частный
случай)
Переменные
состояния
определяются
выражениями
и
модель
вев
находится
как
у
(3.70)
(3.71)
(3.72)
Векторно-матричная
форма
модели
имеет
вид
у
1-~2
-~,
I
х
+ I
~
I
и,
11
О
1
х.
(3.73)
(3.74)
О
Прuмер
3.2.
Модель
ВВ
нагревательной
пе
чи,
RС-цепочки
и
разгона
электродвигателя
(см.
примеры
1.1
и
2.2)
описывается
диффе
ренциальным
уравнением
Tx(t)
+ x(t) = ](u(t),
где
и
-
входное
воздействие
(напряжение),
х
-
выходной
сигнал
(температура,
выходное
напряжение
или
угловая
скорость
соответственно).
Модель
вев
имеет
вид
х
=
-ах+Ьu,
у
х,
где
а
=
l/Т,
Ь
=
К/Т.
(3.75)
(3.76)
О

3.2.
МdДЭЛИ
управляемых
систеМ
99
Прuмер
3.3.
Модель
движения
(вра
щения)
электродвигателя
(см.
при мер
2.3)
описывается
уравнением
второго
порядка
Ту
+
iJ
=
I<и,
где
у
= Q -
угол
поворота.
Введем
в
рассмотрение
переменные
состояния
(3.70),
где
Х2
= W =
й
-
угловая скорость
вращения,
и
найдем
модель
ВСВ
как
у
=
Xl·
Векторно-матричная
форма
модели
имеет
вид
I
~
!а
I
х
+ I
~
I
и,
у
11
О
1
Х.
Это
частный
случай
полученной
ранее
модели
(3.73)-(3.74).
(3.77)
(3.78)
(3.79)
(3.80)
О
Прuмер
3.4.
Рассмотрим
дифференциальное
уравнение
второго
порядка
аоу
=
и,
описывающее
движение
материальной
точки
или
вращение
кинематического
ме
ханизма
(см.
при
мер
2.4).
Уравнение
приводится
к
виду
у
=
Ьи,
где
Ь
=
l/ао.
Введем
в
рассмотрение
переменные
состояния
(3.70)
и
найдем
модель
вев
как
Ьu,
у
Векторно-матричная
форма
модели
име.ет
вид
х
= J
~
~
J
х
+ J
~
J
и,
у
11
О
I
Х.
Это
частный
случай
ранее
рассмотренной
модели
(3.79)-(3.80).
(3.81)
(3.82)
