Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.


120
Глава
4.
Построение
моделей
систем
управления
4.2.
Модели
задающих
блоков
и
внешних
воздействий
Для
описания
внешней
среды,
объектов
слежения
и
генерации
задающих
воз
действий
в
системах
программного
управления
возникает
необходимость
в
кон
струировании
дополнительных
динамических
моделей
-
генераторов
внешних
воздействий,
выходами
которых
являются
возмущающие
j(t)
или
задающие
y"'(t)
воздействия
(см.
1.2.1
и
1.5.2).
Для
гладких
функций
j(t)
и
y*(t)
соответствующие
генераторы
возмущающих
и
задающих
воздействий
могут
быть
получены
в
классе
автономных
линейных
моделей,
аналогичных
рассмотренным
ранее
моделям
(2.2)
или
(3.10)-(3.11).
Так,
генератор
задающих
воздействий
(задающий
блок,
ЗБ)
может
быть
описан
однородным
дифференuиальным
уравнением
вида
(4.33)
с
постоянными
коэффициентами
D:i
и
начальными
значениями
y*(i)(O) =
y~и),
i =
О,
s - 1
( 4.34)
или
соответствующими
векторно-матричными
уравнениями
состояния
х*
=
А*х*
(4.35)
и
выхода
у*
=
С*х*,
(4.36)
где
х*
=
{хn
=
{y*(i-l)}
-
s-мерный
вектор
заданий
(состояния
генератора)
с
начальными
значениями
координат
Xi(O) =
y(~(i-l).
~
~
Генератор
гладких
возмущающих
воздействий
(модель
внешней
среды,
ве)
описывается
однородным
уравнени
ем
( 4.37)
с
постоянными
коэффициентами
"'(i
и
начальными
значениями
или,
в
компактной
форме,
~
j
Г~,
H~,
( 4.38)
(4.39)
(
4.40)
где
~
=
{~i}
=
{j(i-l)}
-
т-мерный
вектор
состояния
внешней
среды
с
начальными
значениями
координат
~i(O)
=
j~i-l).

4.2.
Модели
задающих
блоков
и
внешних
воздействий
121
Воздействия,
генерируемые
рассмотренными
моделями,
соответствуют
решениям
дифференциальных
уравнений
(4.35)-(4.36)
и
(4.39)-(4.40),
т.
е.
определяются
выражением
y*(t) = C*eA·txo
для
задающего
блока
и
выражением
f(t)
=
Hert~o
для
внешней
среды.
С
помощью
указанных
моделей
могут
быть,
в
частности,
получены:
полиномиальные
воздействия
где
СО,
С
1
,
С
2
,
.••
,
С
8
-
1
-
постоянные,
определяемые
как
С
*и-1)
i =
уа
;
многочастотные
гармонические
воздействия
о'
y*(t) = L A
i
sin(wi
t
+
Ч'i),
i=l
(4.41)
(4.42)
(4.43)
(4.44)
(4.45)
где
A
i
,
Ч'i
и
Wi
-
постоянные,
соответствующие
амплитудам,
фазам
и
частотам
гармоник.
Для
нахождения
модели
воздействия
по
заданной
функции
y*(t)
(или
f(t»
мож
но
воспользоваться
методом
последовательного
дифференцирования
соответству
ющих
аналитических
выражений
вида
(4.43)
или
(.4.45).
Пример
4.1.
Для
построения
модели
постоянного
сигнала
y*(t) =
со,
(4.46)
соответствующего
задающему
воздействию
в
задачах
стабилизации,
продифферен
цируем
(4.46)
по
времени.
Получим
уравнение
первого
порядка
y*(t) =
о
(4.47)
у*
о
~I
~
j!
у:
t
у'
о
fl------
·t

122
Глава
4.
Построение
моделей
систем
управления
с
начальным
значением
у*(О)
=
со.
Модель
реализуется
с
помощью
одного
инте
гратора.
Модель
линейно
нарастающего
сигнала
(равномерного
движения)
(4.48)
получается
двукратным
дифференцированием.
На
первом
шаге
находим
(4.49)
а
на
втором
-
искомое
дифференциальное
уравнение
y*(t) =
О,
(4.50)
Для
получения
начальных
условий
из
уравнения
(4.48)
найдем
у*
(О)
=
О,
а
из
уравнения
(4.49) -
у*
(О)
=
С
1
.
Модель
реализует~я
с
помощью
двух
интеграторов.
у*
о
t
Уравнение
(4.50)
приводится
к
форме
модели
состояния
(системе
уравнений
в
форме
Коши).
Для
этого
кроме
основной
переменной
состояния,
совпадающей
с
выходной
переменной
у*
(t),
вводится
вторая
переменная
V*
(t)
(скорость
движе
ния):
у*
(t) =
V*
(t) (4.51)
с
начальным
значением
V*
(О)
:;=
у*(О)
=
С
1
.
Уравнение
(4.50)
можно
переписать
в
виде
V*(t)
=
О.
(4.52)
Полученные
уравнения
(4.51)
и
(4.52)
описывают
искомую
модель
состояния
зада
ющего
блока.
Отметим,
что
решение
(4.48)
уравнения
(4.50)
или
системы
(4.51)-(4.52)
можно
записать
в
виде
у*
(t) =
Уа
+
Vo*t.
(4.53)
Модель
квадратично-нарастающего
сигнала
(равноускоренного
движения)
(4.54)
получается
в
результате
процедуры
трехкратного
дифференцирования
выражения
(4.54)
и
имеет
вид
( 4.55)

4.2.
Модели
задающих
блоков
и
внешних
воздействий
123
с
начальными
условиями
у*(О)
=
СО,
у*(О)
=
С
1
И
у(О)
=
С
з
.
Модель
реализуется
с
помощью
3-х
интеграторов.
у*
о
t
Для
построения
модели
состояния
рассматриваемого
зада
ющего
блока
вводятся
переменные
состояния
y*(t),
V*(t),
a*(t),
где
a*(t) = l1*(t,) -
ускорение,
и
после
их
дифференцирования
по
времени
и
соответствующих
подстановок
получается
система
уравнений
у*
(t)
l1*(t)
a*(t) =
V*(t),
a*(t),
О
с
начальными
значениями
у*
(О)
=
со,
V*
(О)
=
С
1
,
а*
(О)
=
С
2
.
(4.56)
(4.57)
(4.58)
Решение
(4.54)
уравнения
(4.55)
или
системы
(4.56)-(4.58)
можно
записать
в
виде
*(
) *
T.r*t
1
*t2
у
t =
уо
+ v
О
,+
'2
ао
.
(4.59)
о
При.мер
4.2.
Для
генерации
простейшего
гар.монического
воздействия
с
частотой
W,
т.
е.
сигнала
y*(t) = Asill(Wt +
<р),
используется
модель
одночастотного
линейного
осциллятора
(консервативного
зве
на,
см.
п.
2.3):
(4.60)
Значения
амплитуды
колебаний
А
и
фазового
сдвига
<р
определяются
начальными
значениями
модели
у(О)
и
У(О).
у*
о
t

124
Глава
4.
Построение
моделей
систем
управления
Модель
(4.60)
легко
приводится
к
форме
Коши
(4.61)
с
выходом
у*
=
Хl·
Здесь
введены
следующие
обозначения:
(4.62)
Хl
=
у*
,
Х2
=
у*.
( 4.63)
в
частном
случае
для
построения
генератора
сигнала
у*
( t) =
А
sin wt
(4.64)
вводятся
переменные
состояния
Хl
у*
=
Asin
wt,
Х2
=
у*
=
Aw
cos wt.
с
начальными
значениями
Хl
(О)
=
О,
Х2(0)
= Aw.
(4.65)
(4.66)
(4.67)
После
дифференцирования
по
времени
выражений
(4.65), (4.66)
и
соответствую
щих
подстановок
получаем
систему
уравнений
(4.61). D
Замечание
4.1.
Если
переменные
состояния
линейного
осциллятора
(4.60)
выбрать
как
Хl
у*
=
Asin
wt,
Х2
=
Acos
wt
(4.68)
( 4.69)
с
начальными
значениями
Хl
(О)
=
О,
Х2(0)
=
А,
то
модель
состояния
задающего
генератора
примет
вид
(4.70)
Для
генерации
негладких
функций
y*(t)
и
f(t)
используются
модели
с
переменной
структурой
[4,
29]
и
возмущенные
(неавтономные)
линейные
модели
вида
(4.71)
где
u* =
u*(t)
-
негладкое
(может
быть,
разрывное)
входное
воздействие
модели.
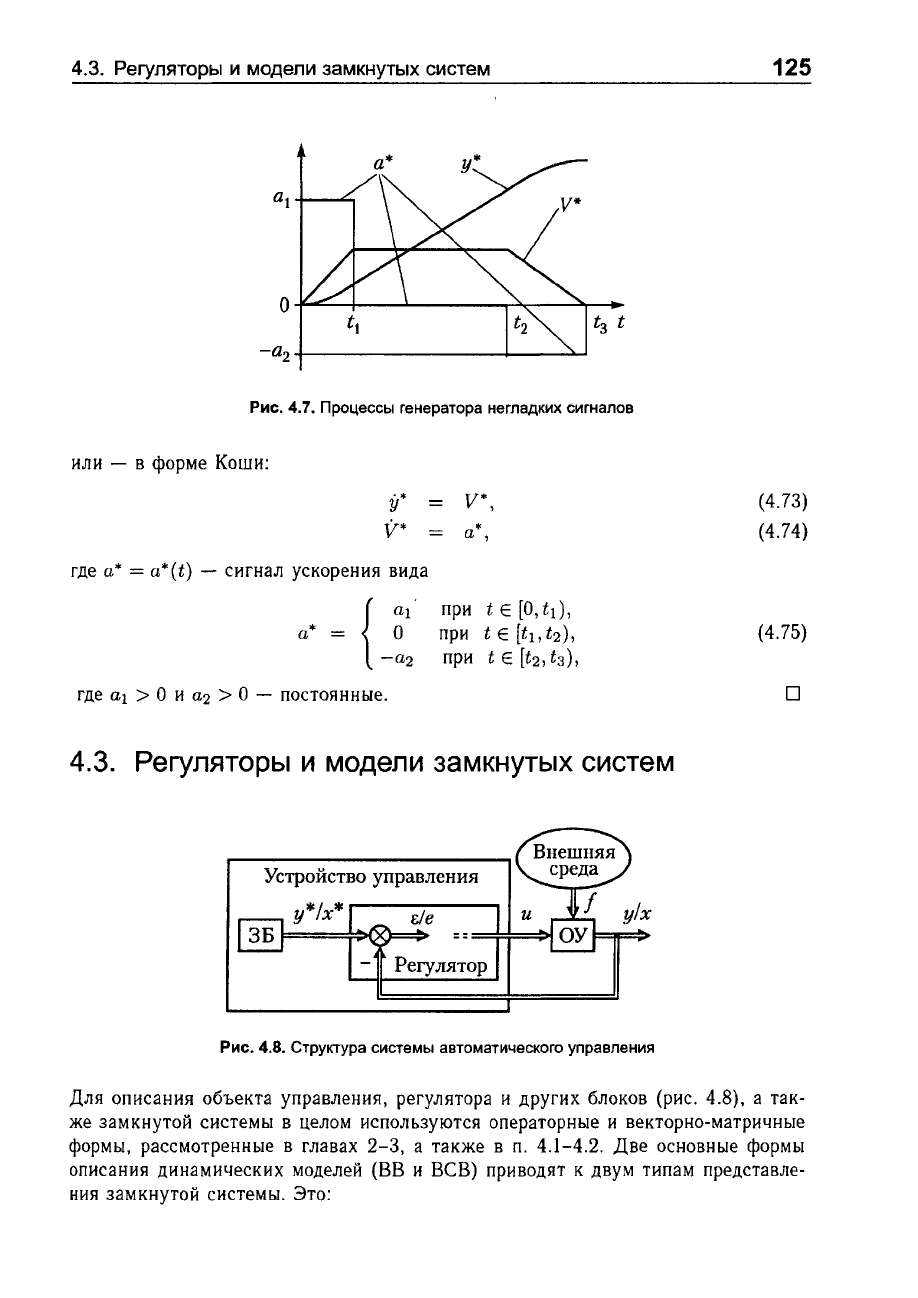
Пример
4.3.
Для
получения
сигнала
y*(t)
с
трапецеидальным
графиком
скорости
V*
=
y*(t)
(рис.
4.7)
можно
воспользоваться
моделью:
..
* *
у
=
а
,
(4.72)
4.3.
Регуляторы
и
модели
замкнутых
систем
-a2+-----------------~--~~
Рис.
4.7.
Процессы
генератора
негладких
сигналов
или
-
в
форме
Коши:
V*
[/
=
V*
*
=
а,
,
где
а*
=
a*(t)
-
сигнал
ускорения
вида
а*
{
аl
-~2
где
аl
>
О
И
а2
>
О
-
постоянные.
при
t
Е
[О,
tl),
при
t
Е
[tl, t2),
при
t
Е
[t2,
t
з
),
4.3.
Регуляторы
и
модели
замкнутых
систем
Устройство
управления
у*/х*
&/е
Регулятор
Рис.
4.8.
Структура
системы
автоматического
управления
125
(4.73)
(4.74)
(4.75)
D
Для
описания
объекта
управления,
регулятора
и
других
блоков
(рис.
4.8),
а
так
же
замкнутой
системы
в
целом
используются
операторные
и
векторно-матричные
формы,
рассмотренные
в
главах
2-3,
а
также
в
п.
4.1-4.2.
Две
основные
формы
описания
динамических
моделей
(ВВ
и
ВСВ)
приводят
к
двум
типам
представле
ния
замкнутой
системы.
Это:

126
Глава
4.
Построение
моделей
систем
управления
•
операторная
(
«классическая»)
модель
вход-выход,
описывающая
связи
зада
ющего
y*(t)
и
возмущающего
f(t)
воздействий
с
выходной
переменной
y(t)
с
использованием
передаточных
функций
(см.
главу
2);
•
векmорно-маmрuчная
(<современная»)
модель,
описывающая
все
блоки
си
стемы
как
модели
вход-состояние-выход
или
состояние-выход
и
ориентиро
ванная
на
использование
метода
пространства
состояний
(см.
главу
3).
Соответствующее
описание
системы
находится
в
результате
объединения
моделей
ее
блоков
с
использованием
известных
правил
преобразования
(в
том
числе
ме
тодов
преобразования
передаточных
функций,
рассмотренных
в
п.
2.4,
и
метода
расширения
пространства
состояний
[20]).
4.3.1.
Операторные
модели
Для
получения
классической
формы
описания
замкнутой
системы
используется
операторная
модель
вход-выход
объекта
управления
(2.34),
то
есть
(4.76)
где
Wo(p)
-
передаточная
функция
ОУ,
Wf(p) -
передаточная
функция
по
воз
мущающему
воздействию,
и
операторная
модель
регулятора.
Рассмотрим
систему
с
наиболее
простым
регулятором
отклонения
(рис.
4.9).
Ре
гулятор
описывается
операторным
уравнением
и
= K(p)€ =
]{(р)
(у*
-
у),
(4.77)
где
рассогласование
(отклонение)
€
рассчитывается
по
формуле:
€ =
у*
-
у,
(4.78)
К(р)
-
интегро-дифференциальный
оператор
обратной
связи
(передаточная
функция
регулятора).
В
зависимости
от
частной
реализации
оператора
]((р)
различают
пропорциональные
(П),
пропорционально-дифференциальные
(ПД),
пропорционально-интегральные
(ПИ)
и
пропорционально-интегрально
дифференциальные
(ПИД)
обратные
связи
(см.
1.5.1
и
п.
7.2).
у
Рис.
4.9.
Система
с
регулятором
отклонений

4.3.
Регуляторы
и
модели
замкнутых
систем
127
Подставляя
(4.77)
в
уравнение
ОУ
(4.76),
после
простейших
преобразований
по
лучаем
уравнение
замкнутой
системы
у
=
или
где
у
=
Ф(р)у*
+
Фf(р)f,
Wo(p)I«(p)
Ф(р)
= 1 + Wo(p)K(p)
-
передаточная
функция
замкнутой
системы
(по
задающему
воздействию),
(4.79)
(4.80)
(4.81)
-
передаточная
функция
замкнутой
системы
по
возмущающему
воздействию.
Замыкание
системы
приводит
к
изменению
ее
передаточных
функций
(ср.
вы
ражения
(4.76)
и
(4.79))
и,
следовательно,
динамических
свойств
и
точностных
показателей
(см.
п.
7.2).
При
этом
с
помощью
обратной
связи
(составляющей
К(р)е)
обеспечиваются
заданные
динамические
свойства
переходного
процесса,
а
точность
системы
зависит
также
от
оператора
Wf(p).
Теперь
рассмотрим
систему
с
регулятором
комбинированного
типа
(рис.
4.10),
ко
торый
в
наибольшей
степени
позволяет
реализовать
возможности
классических
подходов
теории
управления
(см.
п.
7.1).
Регулятор
описывается
операторным
урав-
нением
(4.82)
где
L(p)
и
Lj(p)
-
интегро-дифференциальные
операторы
прямых
связей
по
зада
ющему
и
возмущающему
воздействиям
соответственно.
Подставляя
(4.82)
и
(4.78)
в
уравнение
ОУ
(4.76),
после
простейших
преобразований
получаем
уравнение
замкнутой
системы
комбинированного
упрщ~ления
выходной
переменной
Wo(p)(I«(p) + L(p)) * Wf(p) +
И'о(р)Lf(р)
f
у
= 1 + Wo(p)K(p)
У
+ 1 + Wo(p)I«(p)
(4.83)
у*
Рис.
4.10.
Система
комбинированного
управления
выходом

128
Глава
4.
Построение
моделей
систем
управления
или
выражение
(4.80),
где
передаточные
функции
замкнутой
системы
по
задаю
щему
и
возмущающему
воздействиям
определяются
выражениями
Ф(р)
= Wo(p)(K(p) + L(p))
1 + Wo(p)K(p)
соответственно.
Наличие
прямых
связей
приводит
к
изменению
передаточных
функций
системы
и
ее
точностных
показателей
(см.
п.
7.2).
При
этом
выбор
операторов
прямых
связей
L(p)
и
L f
(р)
осуществляется
из
условия
компенсации
возмущающего
влияния
задающего
воздействия
у*
и
возмущения
/.
Так,
если
в
алгоритме
управления
(4.82)
принять
1
L(p) =
Wo(p)
,
то
уравнение
замкнутой
системы
(4.80)
примет
вид
y(t) = y*(t),
т.
е.
обеспечивается
абсолютная
точность
слежения
и
полная
компенсация
влияния
возмущения
J.
Таким
образом,
модели
замкнутых
систем
с
рассмотренными
типами
регуляторов
представлены
операторными
уравнениями
(4.80).
Последние
легко
преобразуются
к
виду
(4.84)
где
ас(р),
ьс(р),
dc(p) -
характеристические
полиномы
замкнутой
системы.
4.3.2.
Векторно-матричные
модели
в
общем
случае
в
состав
модели
системы
автоматического
управления
входят
следующие
блоки
(рис.
4.11):
объект
управления
СУ:
у
Ax+Bu+DJ,
Сх;
Рис.
4.11.
Система
управления
состоянием
(4.85)
(4.86)

4;3.
Регуляторы
и
модели
замкнутых
систем
задающий
блок
ЗБ
(генератор
задающего
воздействия):
±*
=
А*х*,
у*
=
С*х*;
модель
внешней
среды
ве
(генератор
возмущающего
воздействия):
~
=
Г~,
f =
H~;
регулятор
состояния
(алгоритм
управнения)
Р.
129
(4.87)
(4.88)
(4.89)
(4.90)
Рассмотрим
систему
с
простейшим
nроnорциональным
регулятором
состояния
(рис.
4.12).
В
случае
когда
размерности
векторов
х
и
х*
совпадают,
регулятор
описывается
алгебраическим
уравнением
и
=
Ке,
(4.91)
где
К
-
матрица
коэффициентов
обратной
связи
по
вектору
рассогласований
(от
клонений)
е,
который
рассчитывается
по
формуле:
е
=
х*
-
х.
(4.92)
Рис.
4.12.
Система
управления
с
пропорциональным
регулятором
состояния
Подставив
алгоритм
(4.91),
а
также
уравнения
(4.92)
и
(4.90)
в
уравнение
ОУ
(4.85),
получим
± =
Асх
+
DH~
+
BI(x*,
(4.93)
где
Ас
=
А
-
ВК
-
матрица
замкнутой
системы,
определяющая
ее
динамиче
ские
свойства.
Точность
воспроизведения
задающего
воздействия
также
зависит
от
выбора
матрицы
К
(см.
п.
7.3).
Замечание
4.2.
В
отличие
от
регуляторов
выхода
канонические
алгоритмы
управ
ления
состоянием
не
используют
динамических
операторов,
что
обеспечивает
бо
лее
простую
аппаратную
или
программную
реализацию
устройства
управления.
Тем
не
менее
построение
системы
управления
в
целом
осложняется
необходимо
стью
применения
достаточного
числа
измерительных
устройств
(датчиков).
В
тех
5
зu.6
