Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.

1'40
Глава
5.
Устойчивость
и
структурные
свойства
Более
общим
является
следующий
результат
(34].
Свойство
5.1.
Пусть
f(t)
и
y*(t) -
ограниченные
функции.
Если
автономная
система
(5.1)
или
(5.2)-(5.3)
(асимптотически)
устойчива,
то
существует
частное
решение
yy(t),
и
для
любых
начальных
значений
уи)(о),
i =
О,
n -
1.
выполняется
lim y(t) = yy(t).
t-oo
-
у
о
t
Рис.
5.5.
Переходные
процессы
неустойчивой
системы
управления
Для
неустойчивой
линейной
системы
(см.
определение
5.3)
свободная
составляю
щая
переходного
процесса
расходится,
а
во
многих
случаях
неограниченно
возрас-
тает:
Нт
IYCB(t)1
=
00.
t-oo
(5.28)
Это
приводит
к
неограниченному
росту
выходной
переменной
y(t)
(рис.
5.5)
и
нарушению
целевых
условий
(5.24)-(5.25).
у
о
t
Рис.
5.6.
Переходные
процессы
нейтрально
устойчивой
системы
управления
Для
нейтрально устойчивой
(устойчивой
ГIO
Ляпунову)
системы
(см.
определение
5.2)
свободная
составляющая
переходного
процесса
ограничена:
IYCB(t)1
<
с.
Кро
ме
того,
в
ряде
случаев
(не
всегда!)
текущие
значения
отклонения
вынужденной
составляющей
от
входного
воздействия
y*(t)
также
оказываются
ограниченными,
т.
е.
IYB(t)
-
y*(t)1
<
с',

5.2.
Критерии
устоЙчивости.
141
где
€'
>
О.
Следовательно,
выполняется
Iy(t) - y*(t)1 < € +
е',
т.
е.
выходная
переменная
системы
остается
в
некоторой
окрестности
входного
(задающего)
воздействия
y*(t)
(рис.
5.6).
Таким
образом,
для
нейтрально
устойчивых
систем,
несмотря
на
невозможность
точного
выполнения
целевого
условия
(5.24)
(и
условия
(5.25»,
в
ряде
случаев
удается
обеспечить
его
приближенное
выполнение
(с
точностью
до
эnсилон).
Учитывая
вышеизложенное,
можно
заключить,
что
устойчивость
динамической
системы
является
обязательным
условием
ее
работоспособности
и,
следова
тельно,
одним
из
непременных
требований
при
проведении
синтеза
регуляторов
(см.
главу
7).
5.2.
Критерии
устойчивости
Для
анализа
устойчивости
динамических
систем
можно
воспользоваться
опреде
лениями,
приведенными
в
п.
5.1,
что,
однако,
вызыв~ет
необходимость
исследова
ния
всего
множества
переходных
процессов,
соответствующих
различным
началь
ным
условиям.
Критерии
устойчивости
позволяют осуществить
анализ
системы,
не
прибегая
к
определениям,
т.
е.
на
основании
косвенных
признаков
устойчивости,
связанных
со
свойствами
математических
моделей
(см.
[3,
4,
41]
и
др.).
Здесь
ограничимся
изучением
алгебраических
критериев
устойчивости
линей
ных
систем,
относящихся
к
приведенным
ранее
временным
моделям.
Будем
рас-.
сматривать
автономные
модели
(5.1)-(5.3)
и
соответствующие
решения
и
n
y(t) =
с
Т
eAtxo
= L
Cie
Pit
,
i=l
(5.29)
(5.30)
где
C
i
-
коэффициенты,
зависящие
от
начальных
условий
(см.
2.2.2
и
3.1.3),
Pi
-
полюсы
системы,
или
корни
характеристического
полинома
а(р)
=
det(pI
-
А)
=
рn
+
a1pn-l
+ ... +
а
n
.
(5.31)
Выражения
(5.29)-(5.30)
показывают,
что
свойства
переходных
процессов
в
целом
(а
следовательно,
и
устойчивость
системы)
определяются
свойствами
компоненты
e
At
,
которые,
в
свою
очередь,
зависят
от
полюсов
системы
Pi
=
Лi
{А}
-
корней
характеристического
полинома
(5.31),
или,
что
то
же
самое,
собственных
чисел
матрицы
А.
Это
является
основой
так
называемых
корневых
критериев
устойчи
вости
(см.
5.2.2).

142
Глава
5.
Устойчивость
и
структурные
С80йства
с
другой
стороны,
полюсы
системы
Pi
являются
решениями
ее
характеристическо
го
уравнения
а(р)
=
о
и
зависят
от
коэффициентов
ai.
Поэтому
об
устойчивости
системы
можно
судить
непосредственно
по
значениям
ai
(см.
5.2.1).
Эти
соображения
и
положены
в
основу
алгебраических
критериев,
в
которых
во
прос об
устойчивости
линейной
системы
решаетсн
на
основании
анализа
свойств
чисел
ai
или
Pi
=
Лi{А}.
5.2.1.
Метод
Гурвица
Рассмотрим
характеристическое
уравнение
системы
(5.1):
(5.32)
полагая,
что
ао
>
О,
и
приведем
основные
результаты,
относящиеся
к
понятиям
технической
устойчивости
(см.
определения
5.1
и
5.2).
Свойство
5.2
(теорема
Стодолы).
Если
система
устойчива,
то
коэффициенты
хараКТеристического
уравнения
(5.32)
строго
положительны:
ai
>
О,
i =
г,n.
Отметим,
что
обратное
высказывание
(если
ai
>
О,
то
систе,м,а
устойчива)
спра
ведливо
только
для
систем
l-го
и
2-го
порядков,
чем
и
обусловлена
необходи
мость
более
сложных
условий,
предлагаемых
критериями
Рауса
(1877
г.)
и
Турвица
(1895
г.)
[4,
34].
Ограничимся
рассмотрением
критерия
Гурвица,
для
формулиров
ки
которого
введем
в
рассмотрение
следующие
математические
структуры.
Матрицей
Гурвица
называется
матрица
(таблица)
вида
al
а2
аз
О
О
ао
а2 а4
О
О
О
al
аз
О
О
]У!
О
О О
an-l
О
О О
О
а
n
-2
а
n
а
определителями
Гурвица
-
главные
диагональные
миноры
матрицы
М:
~1

5.2.
Критерии
устойчивости
143
аl
а2
аз
О
ао
а2
а4
О
д
n
-l
О
аl
аз
О
д
П
'МI
=
а
n
д
n
-l'
,
О
О
О
а
n
-l
Свойство
5.3
(критерий
Гурвица)
1.
Система
с
характеристическим
уравнением
(5.32)
устойчива
тогда
и
только
тогда,
когда
все
определители
д
i
строго
положительны,
т.
е.
дi
>
О,
i =
г,n.
2.
Система
нейтрально
устойчива,
если
выполняется
или
{
дi
>
О,'
i =
1,
n -
2,
д
n
-l
=
О,
а
n
>
О.
(5.33)
(5.34)
(5.35)
Замечание
5.6.
С
учетом
того,
что
д
n
(5.33)
можно
представить
в
виде
IMI
=
а
n
д
п
-
1
,
условие
устойчивости
~i
>
О,
i =
1,
n -
1,
а
n
>
о,
(5.36)
в
условии
нейтральной
устойчивости
(5.34)
записать
а
n
=
О,
а
в
условии
(5.35) -
д
n
=0.
Замечание
5.7.
Условие
нейтральной
устойчивости
(5.34)
соответствует
аперио
дическим
установившимся
процессам
системы
и
так
называемой
апериодической
границе
устойчивости.
Условие
(5.35)
соответствует
колебательным
установив
шимся
процессам
и
так
называемой
колебательной
границе
устойчивости
(см.
рис.
5.7-5.8
и
5.2.2).
Пример
5.2.
Рассмотрим
систему
первого
порядка
(n =
1)
аоу
+
аlУ
=
о,
где
ао
>
О.
Здесь
М
=
аl
и,
следовательно,
система
устойчива
тогда
и
только
тогда,
когда
al
>
О.
о

144
Глава
5.
УСТОЙЧИВОСТЬ
И
структурные
СВОЙСТва
Пример
5.3.
Рассмотрим
систему
второго
порядка
(n =
2)
Здесь
М
=1
~'
Если
о
1.
Система
устойчива
при
условиях
а2
~1
=
аl
>
О И
~2
=
О,
т. е.
а2
=
О,
то
система
нейтрально
устойчива
(апериодическая
граница).
Если
же
то
имеет
место
колебательная
граница
устойчивости.
Пример
5.4.
Рассмотрим
систему
третьего
порядка
(n = 3)
Находим
При
условиях
система
устойчива.
Если
у(З)
+
аlУ
+
а2У
+
азу
О.
аl.
аз
О
М
1
а2
О
О
аl
аз
то
имеет
место
апериодическая граница
устойчивости,
а
при
-
колебательная
граница.
о
о
Метод
Гурвица
использован при
доказательстве
известной
теоремы
В.
Л.
Ха
ритонова,
положившей
начало
интервальному
анализу
динамических
систем
(см.
[32J).
5.2.
Критерии
устойчивости
145
5.2.2.
Корневые
критерии
устойчивости
Рассмотрим
систему
с
характеристическим
полиномом
(5.31)
и
полюсами
Pi
=
Лi{А}.
Запишем
Pi
=
Re
Pi
+ j
1т
Pi
и
рассмотрим
составляющие
переходного
процесса
(моды)
Yi(t) = C
i
e
Pit
(5.37)
(см.
также
подраздел
2.2.2).
а
...
t
б
..
t
в
..
t
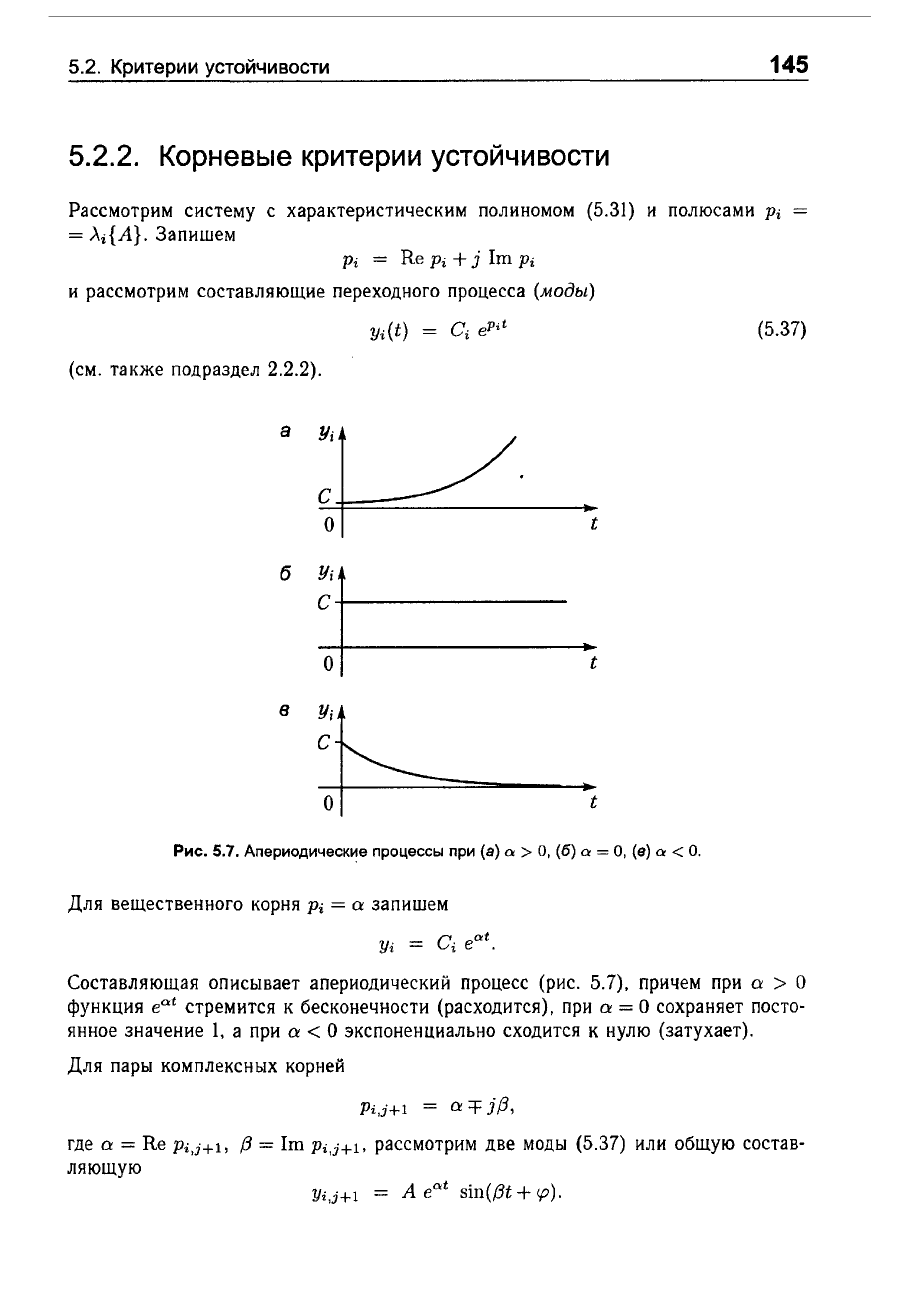
Рис.
5.7.
Апериодическ~е
процессы
при
(а)
а
>
О,
(6)
а
=
О,
(в)
а
<
О.
Для
вещественного
корня
Pi
=
а
запишем
Составляющая
описывает
апериодический
процесс
(рис.
5.7),
причем
при
а
>
О
функция
e
at
стремится
к
бесконечности
(расходится),
при
а
=
О
сохраняет
посто
янное значение
1,
а
при
а
<
О
экспоненциально
сходится
к
нулю
(затухает).
для
пары
комплексных
корней
Pi,j+l =
а
=f
j/З,
где
а
= Re Pi,j+l,
/З
= Im Pi,j+l,
рассмотрим
две
моды
(5.37)
или
общую
состав
ляющую
Yi,j+l =
А
e
at
siп(/Зt
+
<р).
146
Глава
5.
Устойчивость
и
структурные
свойства
а
о
t
б
УЦ+1
А
О
t
-А
в
УЦ+l
Ае
Щ
А
О
t
-А
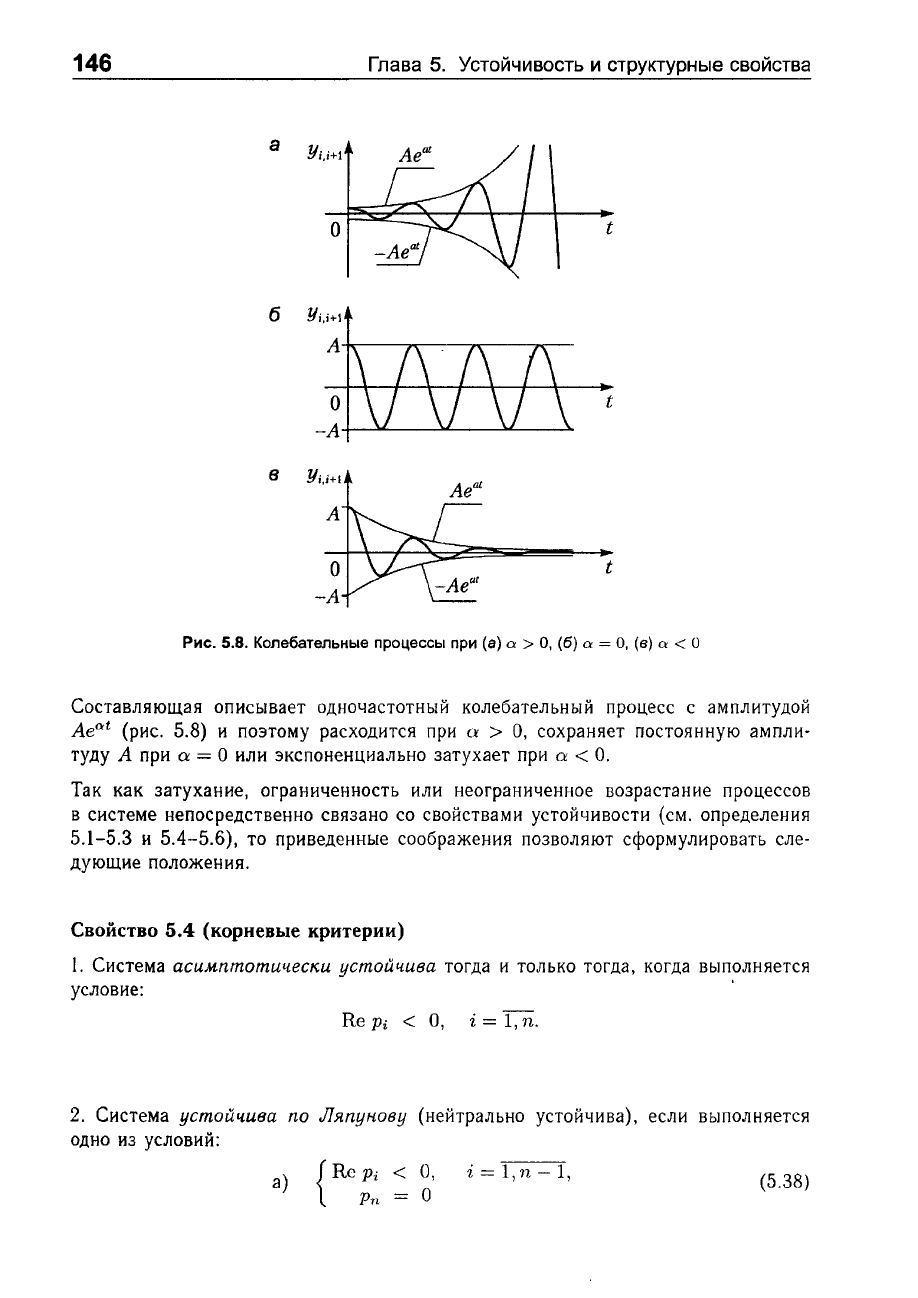
Рис.
5.8.
Колебательные
процессы
при
(8)
о:
>
О,
(6)
о:
=
О,
(в)
о:
< u
Составляющая
описывает
одночастотный
колебательный
процесс
с
амплитудой
AeO:'t
(рис.
5.8)
и
поэтому
расходится
при
СУ
>
О,
сохраняет
постоянную
ампли
туду
А
при
СУ
=
О
или
экспоненциально
затухает
при
СУ
<
О.
Так
как
затухание,
ограниченность
или
неограниченное
возрастание
процессов
в
системе
непосредственно
связано
со
свойствами
устойчивости
(см.
определения
5.1-5.3
и
5.4-5.б),
то
приведенные
соображения
позволяют
сформулировать
сле
дующие
положения.
Свойство
5.4
(корневые
критерии)
1.
Система
асим,nтотически
устойчива
тогда
и
только
тогда,
когда
выполняется
условие:
Re
Pi
<
О,
i =
1,
n.
2.
Система
устойчива
по
Ляпунову
(нейтрально
устойчива),
если
выполняется
одно
из
условий:
а)
{
Re
Pi
<
О,
Рп
О
i =
1,
n -
1,
(5.38)

5.2.
Критерии
устойчивости
(апериодическая
граница
устойчивости)
или
б)
{
Re
Pi
<
О,
Re
Pn-l,n
=
О,
i = 1, n -
2,
1ш
Pn-l,n
=f
о
(колебательная
граница
устойчивости).
3.
Система
неустойчива,
если
найдется
хотя
бы
один
полюс
Pi
такой,
что
а
Re
Pi
>
О.
1т
б
1т
1т
в
1т
о
о
о
о
Re
о
Re
о
Re
о
о
о
о
Рис.
5.9.
Расположение
корней
(а)
асимптотически
устойчивой,
(6)
устойчивой
и
(в)
неустойчивой
системы
147
(5.39)
Re
Критерии
связывают
понятия
устойчивости
с
размещением
корней
на
комплексной
плоскости
(рис.
5.9).
При
этом
расположение
всех
корней
в
левой
полуплоско
сти
эквивалентно
асимптотической
устойчивости
системы,
наличие
хотя
бы
од
ного
корня
в
правой
полуплоскости
делает
систему
неустоЙчивоЙ.
Появление
од
ного
вещественного
или двух
комплексно-сопряженных
корней
на
мнимой
оси
(при
условии
расположения
остальных
корней
в
левой
полуплоскости)
говорит
о
(нейтральной)
устойчивости
системы.
Поэтому
мнимая
ось
называется
границей
устойчивости.
Замечание
5.8.
Апериодическая
граница
устойчивости,
соответствующая
разме
щению
одного
вещественного
корня
на
мнимой
оси,
вызывает
появление
в
системе
незатухающего
апериодического
процесса
(рис.
5.7,
а), а
колебательная
грани
ца,
соответствующая
паре
чисто
мнимых
корней
-
незатухающего
колебательного
процесса
(рис.
5.8,
а).
в
качестве
примеров
простейших
асимптотически
устойчивых
систем
можно
привести
апериодические,
колебательные
и
двойные
апериодические
зве~ья
(см.
п.
2.:?),
полюсы
которых
расположены
в
левой
полуплоскости.
Интегрирующее
звено
имеет
единственный
полюс,
расположенный
на
мнимой
оси,
и
поэтому
(ней
трально)
устойчиво
(апериодическая
граница),
а
консервативное
звено
имеет
два
чисто
мнимых
полюса
и
также
устойчиво
(колебательная
граница).

148
Глава
5.
Устойчивость
и
структурные
свойства
5.2.3.
Уравнение
Ляпунова
и
устойчивые
матрицы
Условие
асимптотической
устойчивости
для
модели
(5.2)
записывается
как
Re
Лi{А}
<
О,
i = 1,n.
(5.40)
Матрица
А,
удовлетворяющая
этому
неравенству,
называется
устойчивой,
или
гурвицевоЙ.
Рассмотрим
алгебраическое
уравнение,
известное
как
уравнение
Ляпунова
[2,
9,
16,
44]:
(5.41)
где
Q -
некоторая
симметрическая
положительно
определенная
матрица:
Q =
=
QT
>
О,
Р
=
рТ
-
симметрическая
матрица,
подлежащая
определению
(реше
ние
уравнения
(5.41».
Свойство
устойчивости
матрицы
А
оказывается
непосред
ственно
связанным
с
решением
уравнения
(5.41).
Свойство
5.5
(лемма
Ляпунова).
Матрица
А
устойчива
тогда
и
только
тогда,
когда
для
любых
матриц
Q =
QT
>
О
уравнение
(5.41)
имеет
положительно
опре
деленное
решение:
Р
>
О.
Таким
образом,
существование
указанного
решения
уравнения
Ляпунова
обес
печивает
устойчивость
матрицы
А
и,
следовательно,
в
соответствии
с
корневым
критерием
(5.40) -
асимптотическую
устойчивость
системы.
Для
оценки
качества
сходимости
переходных
процессов
устойчивой
системы
(см.
п.
6.2)
представляет
интерес
следующее
положение,
непосредственно
выте
кающее
из
леммы
Ляпунова.
Рассмотрим
алгебраическое
уравнение
где
а
~
О.
1т
о
о
а
о
Re
(5.42)
Свойства
5.5,
а.
Матрица
А
удовлетворяет
условию
(5.43)
тогда
и
только
тогда,
когда
уравнение
(5.42)
для
любых
Q =
QT
>
О
имеет
положительно
определенное
решение:
р>о.
Условие
(5.43)
при
а
>
О
означает,
что
полюсы
системы
(собственные
числа
мат
рицы
А)
смещены
влево
от
границы
устойчивости
(мнимой
оси)
на
величину.
превышающую
значение
а,
что
предполагает
не
только
асимптотическую
устой
чивость
системы,
но
и
наличие
определенного
запаса
устойчивости
(см.
6.2.4).

5.3.
Структурные
свойства
систем
управления
149
5.3 . .
Структурные
свойства
систем
управления
Проблемы
управляемости
и
наблюдаемости
динамических
систем,
связанные
с
су
ществованием
и
единственностью
решений
основных
задач
управления
-
управ
ления
состоянием
и
наблюдения
(восстановления
переменных
состояния),
а
также
целый
ряд
соответствующих
критериев
впервые
были
сформулированы
в
60-е
годы
в
работах
Р.
Е.
Калмана
[19].
~
~
Здесь
ограничимся
рассмотрением
одноканальных
ди
намических
систем
(объектов
управления)
± =
Ах+Вu,
у
Сх,
(5.44)
(5.45)
где
и
-
скалярное
управляющее
воздействие
(вход
системы),
у
-
скалярная
выход
ная
переменная.
Рассматриваемые
проблемы
непосредственно
,связаны
со
струк
турой
объекта
или
тройки
матриц
(А,
В,
С),
и
поэтому
свойства
управляемости
и
наблюдаемости
относятся
к
структурным
свойствам
ОУ
[19,
20,
40].
В
этом
разделе
критерии
управляемости
и
наблюдаемости
даны
без
доказательств.
Схемы
доказательств
основных
положений
соответствуют
приведенным
в
подраз
деле
8.2.1,
где
рассматриваются
аналогичные
свойства
дискретных
моделей.
5.3.1.
Управляемость
линейных
систем
u
t
Рассмотрим
вопрос
существования
ограниченного
управляющего
воздействия
(т.
е.
функции
и
= u(t),
определенной
при
любых
t
Е
[to,
t
f])'
переводящего
си
стему
(5.44)-(5.45)
из
произвольного
начального
состо
яния
x(to) =
хо
в
произвольную
точку
пространства
состояний
x(t
f)
=
х
f
за
конечное
время
Т
= t f - to.
Ес
ли
такое
управление
существует,
то
линейная
система
является
полностью
управляемой;
в
противном
случае
говорят
о
неуnравляемости
или
частичной
управляе
мости
системы.
Определение
5.8.
Система
(5.44)-(5.45)
называется
полностью
управляемой,
если
для
любых
to
~
О
и
Х
2
Х
f
Е
JRn
существуют
t f
~
to
и
ограниченное
управление
и
( t ) , t
Е
[to, t f ]
такое,
что
для
x(to)
=
хо
выполняется
x(tf)
=
xf.
