Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.

160
Глава
6.
Качество
систем
управления
Свободные
составляющие
YCB(t)
и
6"cB(t)
достаточно
хорошо
характеризуют
пере
ходные
режимы
и
многих
возмущенных
систем.
В
установившемся
режиме
выходная
переменная
системы
в
идеальном
случае
должна
быть
идентична
задающему
воздействию:
Yy(t) = y*(t),
(6.8)
что
соответствует
нулевому
значению
установившейся
ошибки
Е
t
у
6"y(t)
= y*(t) - Yy(t).
(6.9)
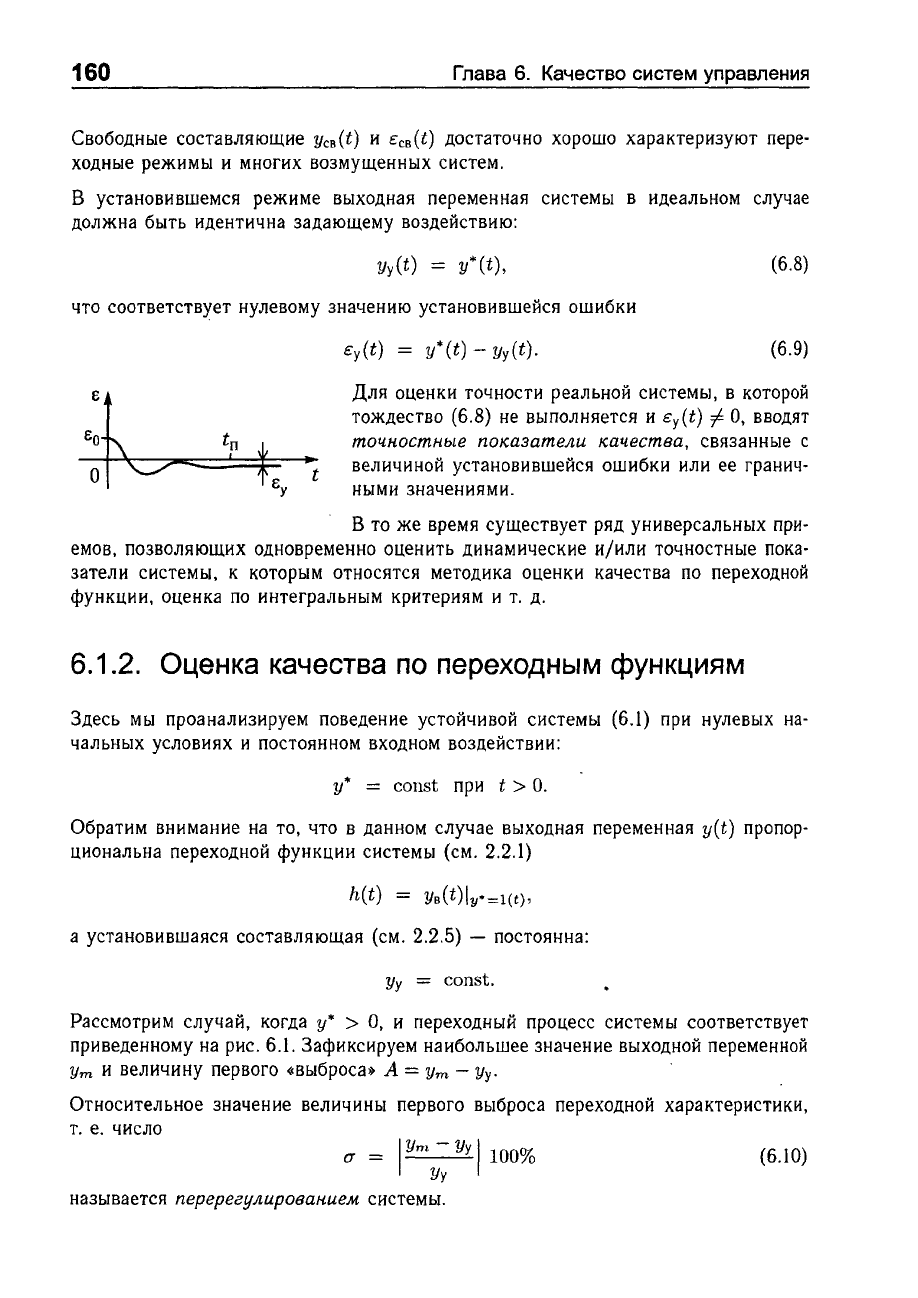
Для
оценки
точности
реальной
системы,
в
которой
тождество
(6.8)
не
выполняется
и
6"y(t)
::/=
О,
вводят
точностные
nоказателu
качества,
связанные
с
величиной
установившейся
ошибки
или
ее
гранич
ными
значениями.
в
то
же
время
существует
ряд
универсальных
при
емов,
позволяющих
одновременно
оценить
динамические
и/или
точностные
пока
затели
системы,
к
которым
относятся
методика
оценки
качества по
переходной
функции,
оценка
по
интегральным
критериям
и
т.
д.
6.1.2.
Оценка
качества
по
переходным
функциям
Здесь
мы
проанализируем
поведение
устойчивой
системы
(6.1)
при
нулевых
на
чальных
условиях
и
постоянном
входном
воздействии:
у*
= const
при
t >
О.
Обратим
внимание
на
то,
что
в
данном
случае
выходная
переменная
y(t)
пропор
цианальна
переходной
функции
системы
(см.
2.2.1)
а
установившаяся
составляющая
(см.
2.2.5) -
постоянна:
Уу
= const.
Рассмотрим
случай,
когда
у*
>
О,
и
переходный
процесс
системы
соответствует
приведенному
на
рис.
6.1.
Зафиксируем
наибольшее
значение
выходной
переменной
ут
И
величину
первого
«выброса»
А
=
Ут
-
Уу.
Относительное
значение
величины
первого
выброса
переходной
характеристики,
т.
е.
число
(j
= I
Yтy~
Уу
1100%
(6.10)
называется
nеререгулuрованuе,м,
системы.

6.1.
Задачи
систем
управления
и
показатели
качества
161
о
t
Рис.
6.1.
Переходная
характеристика
и
динамические
показатели
качества
Отметим,
что
для
линейных
систем
значение
А
пропорционально
входу
у*,
в
то
время
как
перерегулирование
не
зависит
от
входного
воздействия.
Перерегулирование
характеризует
колебательные
свойства
процессов.
При
нуле
вом
значении
(7'
процесс
носит
монотонный
характер,
а
при
достаточно
больших
(7' -
приближается
к
незатухающему
колебательному
движению.
Для
оценки
быстродействия
системы
введем
в
рассмотрение
некоторую
Дп-окрестность
установившегося
значения:
Iy
-
Ууl
<
ДП,
и
выбирем
радиус
окрестности
как
ДП
= 6
n
lY
y
l,
где
положительное
число
6
п
< 1
определяет
относительный
размер
окрестности.
Временем
переходного
nроцесса
называется
значение
t = t
n
такое,
что
Iy(t) -
уу!
:s;
ДП
при
t > t
n
,
т.
е.
интервал
времени,
после
которого
переходный
процесс
развивается
в
пределах
заданной
дп-окрестности
установившегося
значения.
Для
фиксированного
значения
6
п
радиус
рассматриваемой
окрестности
(как
и
зна
чение
Уу)
прямо
пропорционален
у*.
Следовательно,
число
t
n
не
зависит
от
вход
ного
воздействия
у*
и
дает
объективную
оценку
быстродействия.
Выбор
относительной
величины
окрестности
6
п
определяется
требованиями
кон
кретной
задачи.
Обычно
выбирается
6
п
=
0.05,
т.
е.
5-процентная
окрестность
установившегося
значения.
Тогда
t
n
соответствует
времени,
необходимому
для
вы
полнения
неравенства
Iy(t) -
ууl
:S;
0.05у
у
.
Заметим,
что
для
апериодического
звена
t
n
=
3Т
(см.
рис.
2.10).
Рассмотренные
показатели
качества
предназначены
для
анализа
динамических
свойств
САУ.
С
другой
стороны,
заданные
значения
перерегулирования
и
вре
мени
переходного
процесса
определяют
требования
к
желаемому
поведению
раз
рабатываемой
системы
и
используются
при
осуществлении
синтеза
регуляторов
6
Зах.
6
162
Глава
6.
Качество
систем
управления
(см.
п.
6.3
и
7.3.1).
Так,
например,
в
предположении,
что
система
должна
иметь
абсолютную
точность,
т.
е.
Уу
=
у*,
а
задающее
воздействие
у*
>
о
известно,
по
заданной
величине
а
находим
значение
(6.11)
а
по
заданному
значению
tS
n
-
величину
радиуса
окрестности
(6.12)
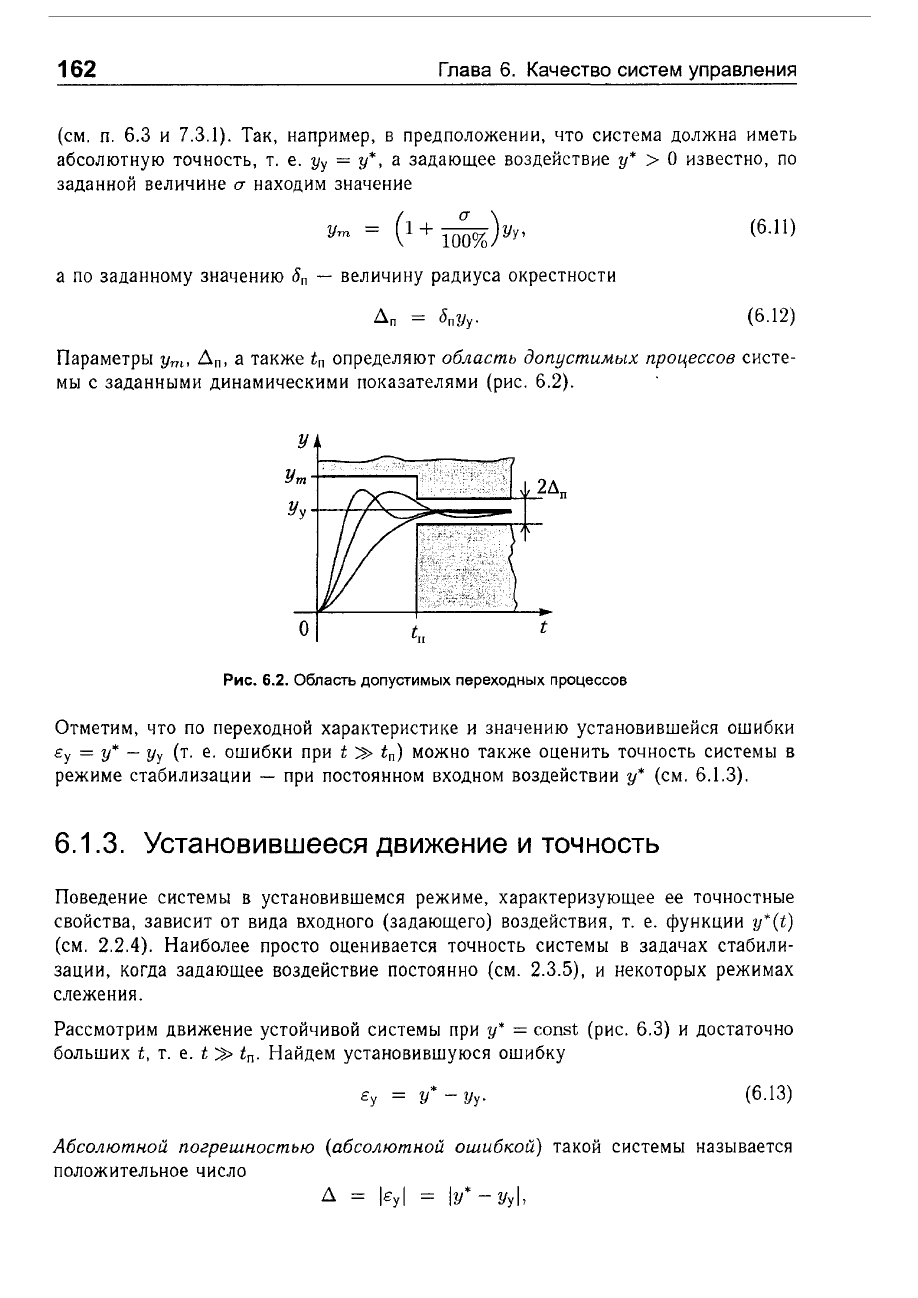
Пара
метры
Уrn,
,6,n,
а
также
t
n
определяют
область
допустимых
nроцессов
систе
мы
с
заданными
динамическими
показателями
(рис.
6.2).
у
yт+-------~,;
2
~------~_f_
д
п
yyт-~~~~~~,-
о
t
Рис.
6.2.
Область
допустимых
переходных
процессов
Отметим,
что
по
переходной
характеристике
и
значению
установившейся
ошибки
€y
=
у*
-
Уу
(т.
е.
ошибки
при
t » t
n
)
можно
также
оценить
точность
системы
в
режиме
стабилизации
-
при
постоянном
входном
воздействии
у*
(см.
6.1.3).
6.1.3.
Установившееся
движение
и
точность
Поведение
системы
в
установившемся
режиме,
характеризующее
ее
точностные
свойства,
зависит
от
вида
входного
(задающего)
воздействия,
т.
е.
функции
y*(t)
(см.
2.2.4).
Наиболее
просто
оценивается
точность
системы
в
задачах
стабили
зации,
когда
задающее
воздействие
постоянно
(см.
2.3.5),
и
некоторых
режимах
слежения.
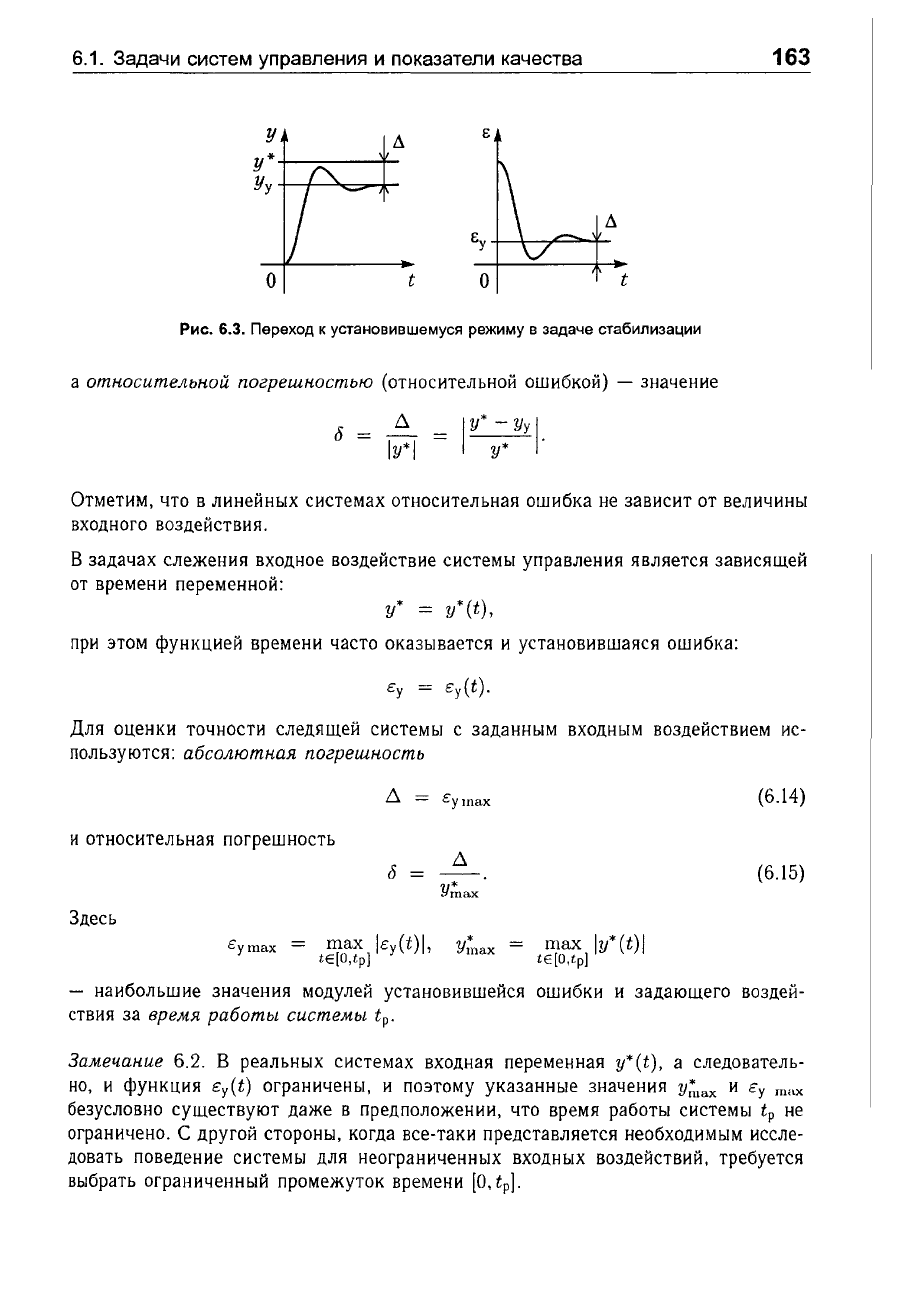
Рассмотрим
движение
устойчивой
системы
при
у*
= const
(рис.
6.3)
и
достаточно
больших
t,
т.
е.
t » t
n
.
Найдем
установившуюся
ошибку
€y
=
у*
-
Уу.
(6.13)
Абсолютной
nогрешностью
(абсолютной
ошибкой)
такой
системы
называется
положительное
число
6.1.
Задачи
систем
управления
и
показатели
качества
У
У
*
-I------'f--
У
у
-I--+-~=--II~
о
t
t
Рис.
6.3.
Переход
к
установившемуся
режиму
в
задаче
стабилизации
а
относительной
nогрешностью
(относительной
ошибкой)
-
значение
б
-
~
- I
у*
-
Уу
I
-
/у*/
-
у*
.
163
Отметим,
что
в
линейных
системах
относительная
ошибка
не
зависит
от
величины
входного
воздействия.
В
задачах
слежения
входное
воздействие
системы
управления
является
зависящей
от
времени
переменной:
у*
=
y*(t),
при
этом
функцией
времени
часто
оказывается
и
установившаяся
ошибка:
€y = €y(t).
Для
оценки
точности
следящей
системы
с
заданным
входным
воздействием
ис
пользуются:
абсолютная
nогрешность
.6.
=
€ушах
и
относительная
погрешность
б
.6.
Y:n'ax
Здесь
€yтax
=
тах
jey(t)/, Y:nax
tE[O,tp]
тах
'у*
(t)/
tE[O,tp]
(6.14)
(6.l5)
наибольшие
значения
модулей
установившейся
ошибки
и
задающего
воздей
ствия
за
время
работы
системы
t
p
.
Замечание
6.2.
В
реальных
системах
входная
переменная
у*
(t),
а
следователь
но,
и
функция
€y(t)
ограничены,
и
поэтому
указанные
значения
y~lax
И
€y
тах
безусловно
существуют
даже
в
предположении,
что
время
работы
системы
t
p
не
ограничено.
С
другой
стороны,
когда
все-таки
представляется
необходимым
иссле
довать
поведение
системы
для
неограниченных
входных
воздействий,
требуется
выбрать
ограниченный
промежуток
времени
[О,
t
p
].
164
Глава
6.
Качество
систем
управления
у
у*
Е
/).
у*
mох
о
t
t
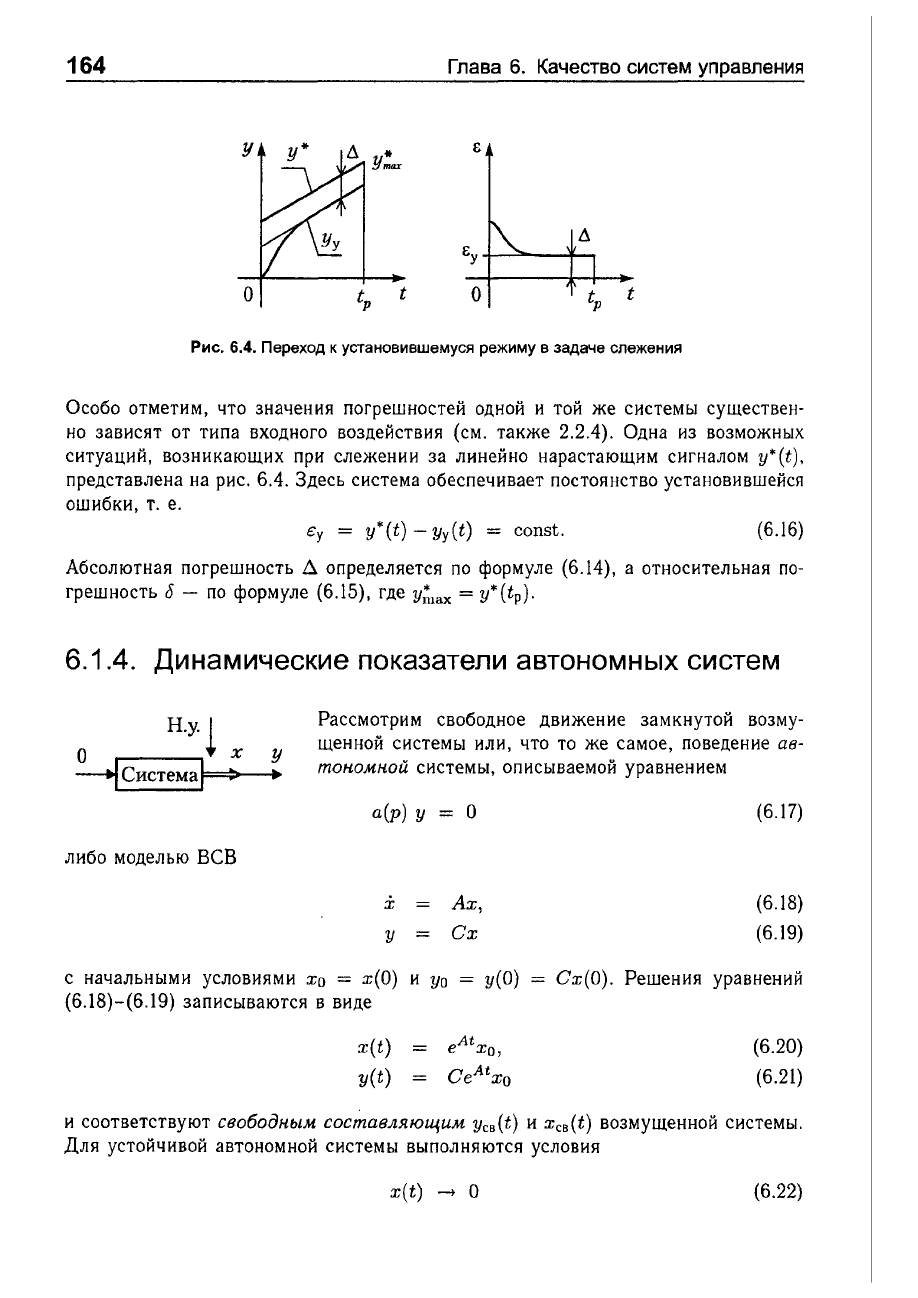
Рис.
6.4.
Переход
к
установившемуся
режиму
в
задаче
слежения
Особо
отметим,
что
значения
погрешностей
одной
и
той
же
системы
существен
но
зависят
от
типа
входного
воздействия
(см.
также
2.2.4).
Одна
из
возможных
ситуаций,
возникающих
при
слежении
за
линейно
нарастающим
сигналом
y*(t),
представлена
на
рис.
6.4.
Здесь
система
обеспечивает
постоянство
установившейся
ошибки,
т.
е.
е
у
= y*(t) - yy(t) = const.
(6.16)
Абсолютная
погрешность
Д
определяется
по
формуле
(6.14),
а
относительная
по
грешность
д
-
по
формуле
(6.15),
где
y~lax
= y*(t
p
).
6.1.4.
Динамические
показатели
автономных
систем
о
н.у.!
х
у
-=--.J
Система
1=1
==:----+~
либо
моделью
веБ
Рассмотрим
свободное
движение
замкнутой
возму
щенной
системы
или,
что
то
же
самое,
поведение
ав
тономной
системы,
описываемой
уравнением
а(р)
у
=
о
х Ах,
у
=
Сх
(6.17)
(6.18)
(6.19)
с
начальными
условиями
хо
=
х(О)
И уо
=
у(О)
(6.18)-(6.19)
записываются
в
виде
Сх(О).
Решения
уравнений
x(t)
eAtxo,
y(t)
= CeAtxo
(6.20)
(6.21)
и
соответствуют
свободным
составляющим
YCB(t)
и
XCB(t)
возмущенной
системы.
Для
устойчивой
автономной
системы
выполняются
условия
x(t)
--+
о
(6.22)

6.1.
Задачи
систем
управления
и
показатели
качества
165
и
y(t)
~
О,
(6.23)
а
для
анализа
ее
динамических
свойств
используются
показатели,
аналогичные
приведенным
в
6.1.2.
Замечание
6.3.
Несмотря
на то
что
для
возмущенных
и
автономных
режимов
определения
ряда
динамических
показателей
работы
кажутся
схожими,
числен
ные
значения
показателей
для
одной
и
той
же
системы
могут
оказаться
различ
ными,
что
объясняется
различием
свойств
переходных
и
свободных
составляющих
рассматриваемых
процессов
(см.
замечание
2.2,
подраздел
2.2.4).
Проанализируем
поведение
выходной
переменной
y(t)
(рис.
6.5).
Быстродействие
автономной
системы
также
характеризуется
временем
переходного
процесса.
Временем
переходного
nроцесса
называется
временной
интервал
[О,
t
l1
]
(или
про
сто
момент
времени
t = t
l1
~
О),
по
окончанию
которого
переходный
процесс
развивается
в
пределах
заданной
.6.
11
-окрестности
положения
равновесия
у
=
О:
Jy(t)J
~
.6.11
при
t > t
l1
•
Радиус
окрестности
.611
определяется
как
где
О
<
811
<
1.
При
выборе
8
п
= 0.05
показатель
t
п
определяется
как
величина
отрезка
времени,
необходимого
для
выполнения
неравенства
/y(t)/
~
0.05
уа.
Колебательные
свойства
автономной
системы
определяются
значениями
перере
гулирования,
затухания,
числом
колебаний
переходного
процесса
и
т.
д.
Наимень
шее
целое
число,
определяемое
по
формуле
У
УО
о
(6.24)
t
Рис.
6.5.
Переходный
процесс
автономной
системы
и
динамические
покаэатели
качества

166
Глава
6.
Качество
систем
управления
где
Т -
период
основной
гармоники
колебательного
процесса,
называется
числом
колебаний
(за
время
переходного
процесса).
Относительное
значение
величины
первого
выброса
переходного
процесса,
т.
е.
(j
= /
~
/100%
(6.25)
называется
перерегулированием.
Затуханием
называется
величина
относительного
уменьшения
амплитуды
коле
баний
выходной
переменной
за
один
период
Т,
т.
е.
(6.26)
где
А
1
=
y(t
1
),
А
2
=
y(t2),
t2 =
tl
+
Т
(рис.
6.6).
Этот
парам€тр
иногда
выражают
в
процентах,
и
он
принимает
значения
от
О
(для
апериодических
процессов)
до
1
(или
100%)
для
незатухающих
колебаний.
у
t
Рис.
6.6.
Затухание
колебательного
процесса
Универсальным
показателем
динамических
свойств
может
служить
интегральная
квадратичная
ошибка
(рис.
6.7),
т.
е.
значение
функционала
(6.27)
о
t
Рис.
6.7.
Определение
интегральной
ошибки
6.1.
Задачи
систем
управления
и
показатели
качества
167
равное
площади
фигуры,
ограниченной
осью
времени
и
функцией
y2(t).
Для
устой
чивых
систем
число
J
y
обычно
ограничено
и
зависит
как
от
быстродействия,
так
и
от
колебательных
свойств
системы.
Быстродействие
системы
можно
также
оценить
по
норме
вектора
состояния
Ix(t)/
(см.
также
6.2.4).
Пусть
начальные
значения
x(t)
принадлежат
до-окрестности
положения
равновесия
х
=
О:
Зададим
также
некоторую
дп-окрестность,
где
и
О
<
д
п
< 1
(рис.
6.8).
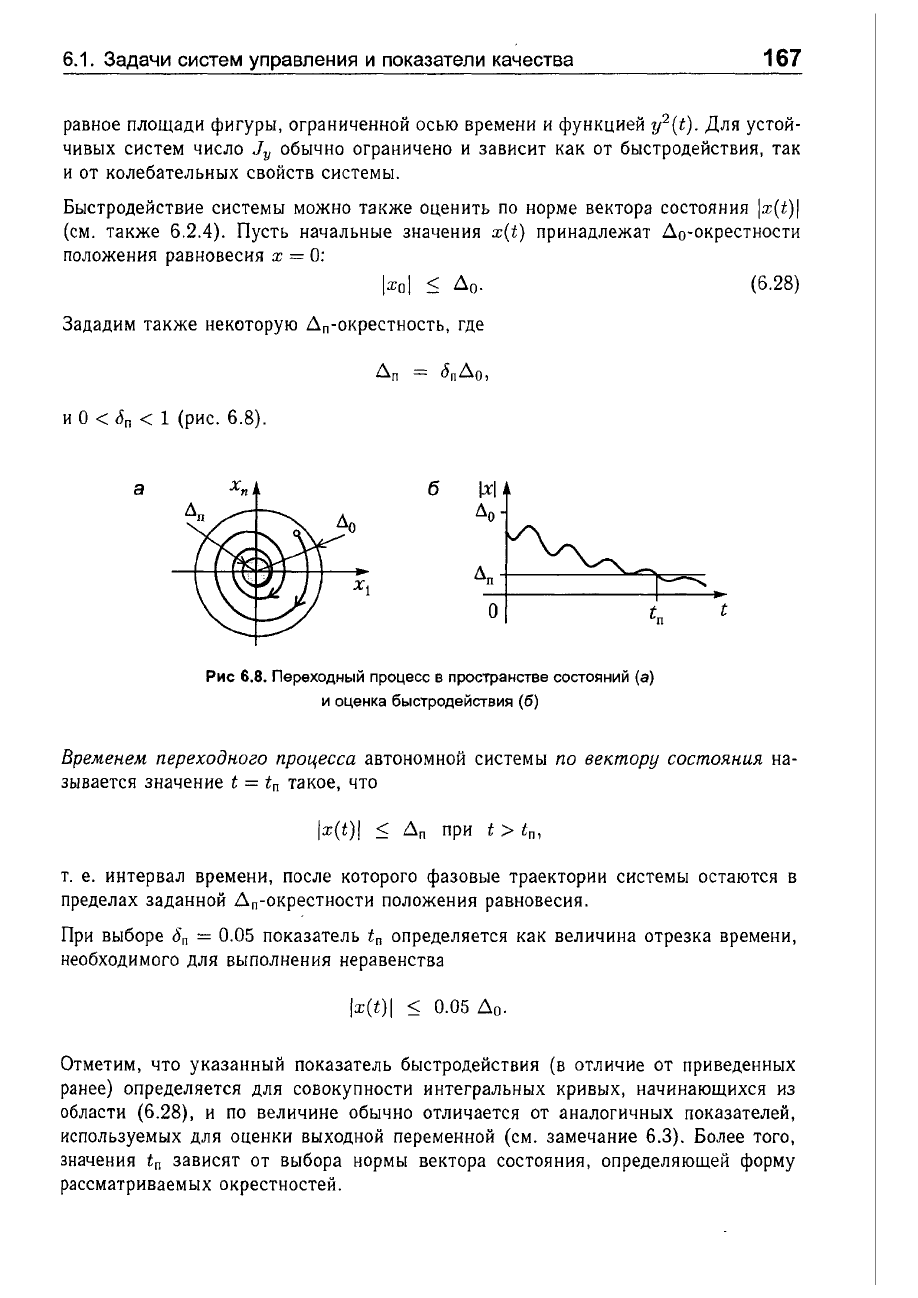
а
б
Рис
6.8.
Переходный
процесс
в
пространстве
состояний
(а)
и
оценка
быстродействия
(б)
(6.28)
t
Временем
переходного
nроцесса
автономной
системы
ПО
вектору
состояния
на
зывается
значение
t = t
n
такое,
что
т.
е.
интервал
времени,
после
которого
фазовые
траектории
системы
остаются
в
пределах
заданной
дп-окрестности
положения
равновесия.
При
выборе
д
п
=
0.05
показатель
t
n
определяется
как
величина
отрезка времени,
необходимого
для
выполнения
неравенства
Ix(t)1
~
0.05
до.
Отметим,
что
указанный
показатель
быстродействия
(в
отличие
от
приведенных
ранее)
определяется
для
совокупности
интегральных
кривых,
начинающихся
из
области
(6.28),
и
по
величине
обычно
отличается
от
аналогичных
показателей,
используемых для
оценки
выходной
переменной
(см.
замечание
6.3).
Более
того,
значения
t
n
зависят
от
выбора
нормы
вектора
состояния,
определяющей
форму
рассматриваемых
окрестностей.

1вs
Для
одновременной оценки
динамических
свойств
системы
используются
также
обобщенные
интегральные
nоказатели
типа
J
x
=
1~
Ix(t)1
2
(t)dt
(см.,
например,
[44]).
6.2.
Корневые
методы
исследования
качества
Корневые
методы
предназначены
для
анализа
динамических
показателей
автоном
ной
системы
или
показателей,
связанных
со
свободным
движением
(см.
6.1.4).
Как
и
соответствующие
критерии
устойчивости,
они
позволяют
осуществить
ана
лиз
системы,
не
прибегая
к
определениям
-
на
основании
косвенных
признаков
и
свойств
математической
модели.
Рассмотрим
устойчивые
автономные
модели
(6.17)-(6.19)
и
соответствующие
ре
шения
дифференциальных
уравнений
(6.20)-(6.21).
Зависимость
этих
решений
от
корней
характеристического
уравнения
системы
Pi
=
>ч
{А}
является
основанием
для
введения
так
называемых
корневых
.методов
анализа
качества.
Сначала
исследуем
задачу
определения
качественных
показателей,
связанных
с
динамикой
выходной
переменной
y(t)
системы
а(р)у
=
О,
(6.29)
где
(6.30)
при
у(О)
=1=-
о
и
нулевых
начальных
значениях
производных,
т.
е.
при
условии
(i)
О'
1 1
уо
= ,
'/,
=
,n
- .
(6.31)
Напомним,
что
(для
случая
неравных
полюсов
системы
Pi)
выходная
переменная
автономной
системы
описывается
выражением
n n
y(t) =
LYi(t)
= L
Cie
Pit
,
(6.32)
i=l i=l
а
из
условия
асимптотической
устойчивости
следует,
что
Re
Pi
<
О,
i = 1,n,
(6.33)
т.
е.
корни
характеристического
полинома
а(р)
расположены
левее
мнимой
оси,
яв
ляющейся
границей
устойчивости.
Более
того,
нетрудно
показать,
что
чем
дальше
полюсы
системы
удалены
от
границы,
тем
выше
скорость
протекания
процессов.

6.2.
Корневые
методы
исследования
качества
169
6.2.1.
Расположение
полюсов
и
теорема
подобия
Сравним
динамические
свойства
системы
(6.29)
и
системы
а'
(р)у'
=
о
(6.34)
с
характеристическим
полиномом
специального
вида
'(
) n +
n-l
+ +
n-l
+ n
а
р
=
р
alwOP
. . .
an-1W
O
Р
anw
o
,
(6.35)
где
Wo
>
О.
Пусть
p~
=
p~(wo)
-
корни
полинома
(6.35).
При
Wo
= 1
получаем,
что
характе
ристический
полином
а'(р)
совпадает
с
полиномом
а(р)
системы
(6.29),
и
p~
= Pi.
В
общем
случае
нетрудно
получить,
что
корни
полинома
а'(р)
связаны
с
полюсами
Pi
простым
выражением
(6.36)
т.
е.
их значения
прямо
пропорщюнальны
wo.
1т
pj
,
Р;
Re
О
~
Таким
образом,
пара
метр
Wo
характеризует
удаление
по
люсов
системы
от
начала
координат
комплексной
плоско
сти.
(В
ряде
случаев,
рассмотренных
в
п.
6.3,
указанный
параметр
соответствует
радиусу
распределени'я
корней).
Выходная
переменная
системы
(6.34)
определяется
выра
жением
n
у'
(t)
'"'"
С.
eP~
t
L...J
~
,
(6.37)
i=l
в
котором
при
условии
(6.31)
значения
неопределенных
коэффициентов
C
i
не
за
висят
от
Wo.
Подставив
(6.36)
в
выражение
(6.37),
получим
n
y'(t) =
2:
Cie
Pi
(,j)ot.
i=l
(6.38)
Сравнение
последнего
выражения
с
формулой
(6.36)
служит
основанием
для
сле
дующего
вывода
(см.
также
рис.
6.9).
Свойство
6.1
(теорема
подобия).
Переходные
процессы
y(t)
системы
(6.29)
с
полюсами
Pi
и
процессы
y'(t)
системы
(6.34)
с
полюсами
p~
связаны
соотношением
y'(t) = y(wot).
(6.39)
Теорема
показывает,
что
удаление
всех
полюсов
системы
от
мнимой
оси
(а
точ
нее,
от
начала
координат
комплексной
плоскости)
при
увеличении
пара
метра
WQ
