Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.

190
а
1
К
1-К
о
Глава
6.
Качество
систем
управления
у.
б
1~---------.~--
Ву
r
~
t
о
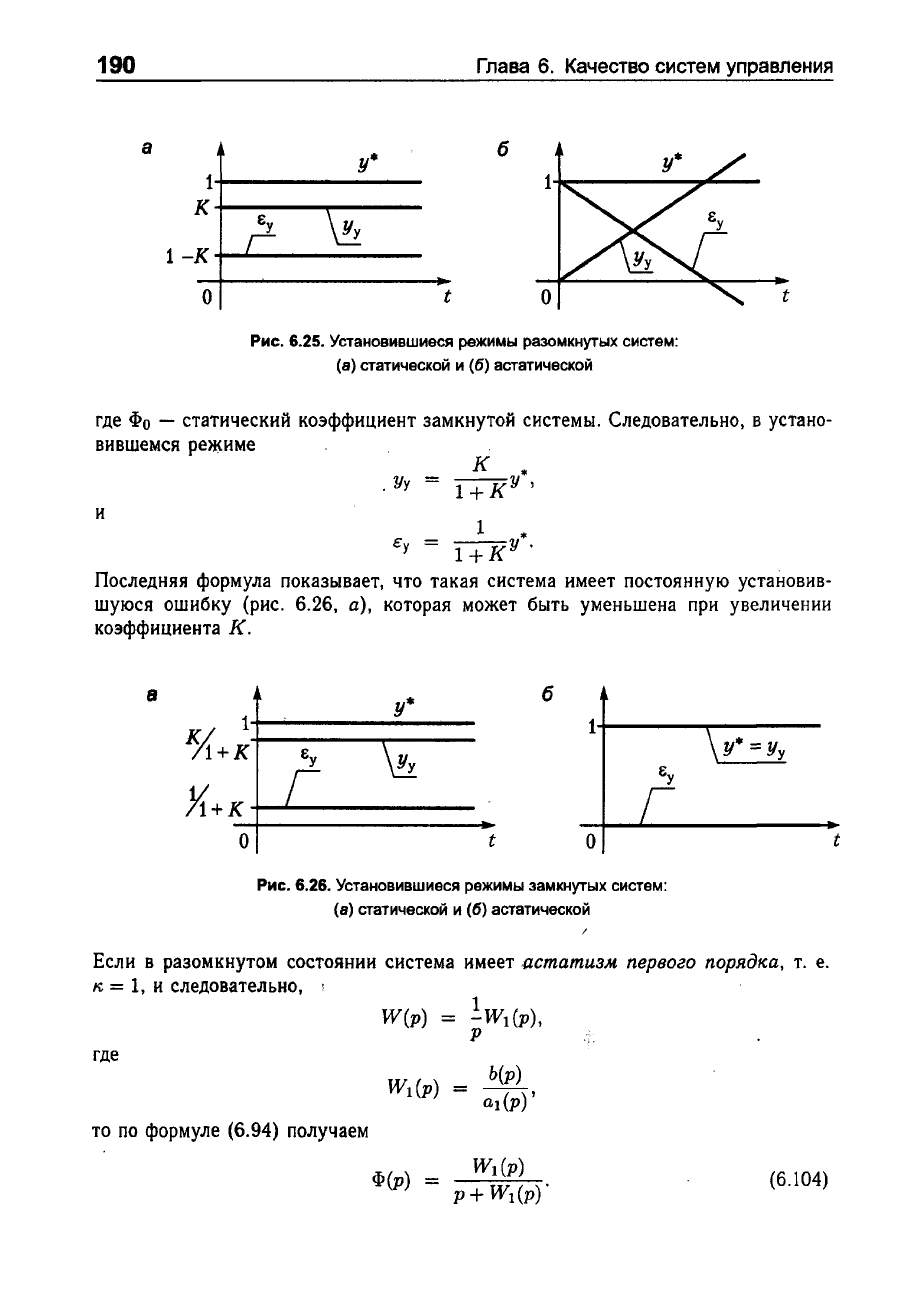
Рис.
6.25.
Установившиеся
режимы
разомкнутых
систем:
(8)
статической
и
(6)
астатической
t
где
Ф
О
-
статический
коэффициент
замкнутой
системы.
Следовательно,
в
устано-
вившемся
ре~име
к
*
.
Уу
= 1
+К
У
,
и
1 *
су
= 1
+К
У
.
Последняя
формула
показывает,
что
такая
система
имеет
постоянную
установив
шуюся
ошибку
(рис.
6.26,
а),
которая
может
быть
уменьшена
при
увеличении
коэффициента
К.
8
o/t1
1+К
К+К
О
у*
б
1
Г
\!6:
Ву
t
О
Рис.
6.26.
Установившиеся
режимы
замкнутых
систем:
(8)
статической
и
(6)
астатической
у.
=Уу
Если
в
разомкнутом
состоянии
система
имеет
,астатuз'м
первого порядка,
т.
е.
к,
=
1,
и
следовательно,
!
где
W
1
(p)
=
Ь(р)
аl
(р)'
то
по
формуле
(6.94)
получаем
Ф(р)
(6.104)
t

6.4.
OцeH~a
T.o~HOCTHЫX
показателе~
Тогда
Ф(О)
==
Ф
О
= 1
и,
следовательно,
в
рассматриваемом
режиме
(рис.
6.26,
б)
Уу
=
У*
и
€y
=
О.
Статические
коэффициенты
невозмущенных
систем
различной
CTQYKT~Pbl
сведены
в
табл.
6.5.
Таблица
6.5.
Статические
коэффициенты
невоэмущенной'системы
Тип
системы
Переменная
Разомкнутая
,
Замкнутая
Статическая
Астатическая
Статическая
Астатическая
у
К
-
K/(l
+К)
1
€
1-К
-
1/(1 +
К)
О
Таким
образом,
повышение
точности
работы
системы
управления
при
ПОС1'оян'·
ном
задающем
воздействии
обеспечивается
ее
замыканием,
повышением
порядка
астатизма
или
увеличением
статического
коэффициента
разомкнутой
части.
Теперь
рассмотрим
систему
управления
при
у*
= const
и
возмущающем
воздей
ствии:
f = const.
В
силу
линейности
рассматриваемых
систем
в
установившемся
режиме
можно
выделить
две
составляющие
процессов.
соответствующие
влиянию
задающего
и
возмущающего
воздействия,
т. е.
* f
Уу
=
уу
+
У
у
'
Для
разомкнутой
системы
(6.89)
в
установившем~я
режиме
получим
Уу
= W(O)y* +
Wf(O)f.
Из
условия
работоспособности
(см.
выше),
полагаем,
что
по
основном!
каналу
си
стема
является
статической.
Тогда
установившаяся
составляющая
Уу,
вызванная
влиянием
возмущения,
и
соответствующа~
составляющая
ошибки
€!
зависят
толь
ко
от
свойств
передаточной
функции
Wf(p).
Для
статической
(по
возмущению)
системы
имеет
место
где
К
f -
статический
коэффициент
передачи
по
возмущению.'
При
f = const,
имеет
место
зависимость

192
Глава
6.
Качество
систем
управления
а
1
К
!
О
f
б
f
1
У
=-;
у у
У
у
=
-&~
К!{
1+К
t
О
Рис.
6.27.
Установивwиеся
режимы
статических
возмущенных
систем:
(а)
разомкнутой,
(6)
замкнутой
и,
следовательно
(рис.
6.27,
а),
€{
=
-у!
='
-](/1.
t
в
том
случае,
когда
разомкнутая
система
по
возмущению
является
астатической,
она
не
имеет
определенных
установившихся
значений
у{
и
€(.
Модель
вход-выход
замкнутой
возмущенной
системы
имеет
вид
(6.93)
и,
следова-
уу
=
Ф(О)у·
+
Ф
/(0)/.
Ее
свойства
зависят
от
передаточных
функций
разомкнутой
системbI
W(p)
и
W/(p).
Если
разомкнутая
система
-
статическая
по
всем
входам,
то
по
фор
м.уле(6.95)
определяем
Следовательно.
и
!(/
/
l+К
/ /
К/
€y
=
-Уу
= - 1 +
к/
(рис.
6.27,
6).
Последняя
формула
показывает,
что
такая
система
имеет
постоян
ную
установившуюся
ошибку,
которая
может
быть
уменьшена
за
счет
увеличения
статического
коэффициента
К.
В
случае
когда
разомкнутая
система
является
астатической
(по
основному
кана
лу)
и
статической
по
возмущающему
воздействию,
по
формуле
(6.95)
с
учетом
(6.104)
получаем
ф
(р)
='
pW/(p)
.
/
р+
W
1
(p)
Тогда
Ф
/(0) =
О
и,
следовательно,
у{
=
€?
=
О
(рис.
6.28,
а).
Если
же
разомкнутая
система
является
астатической
по
обоим
каналам,
то
6}~:"
Оценка
точностных
покаэателей
а
f
б
f
1
1
У
=-ё.l
К/
Ук
у
=-/
у
у
у
у
К1
О
t
О
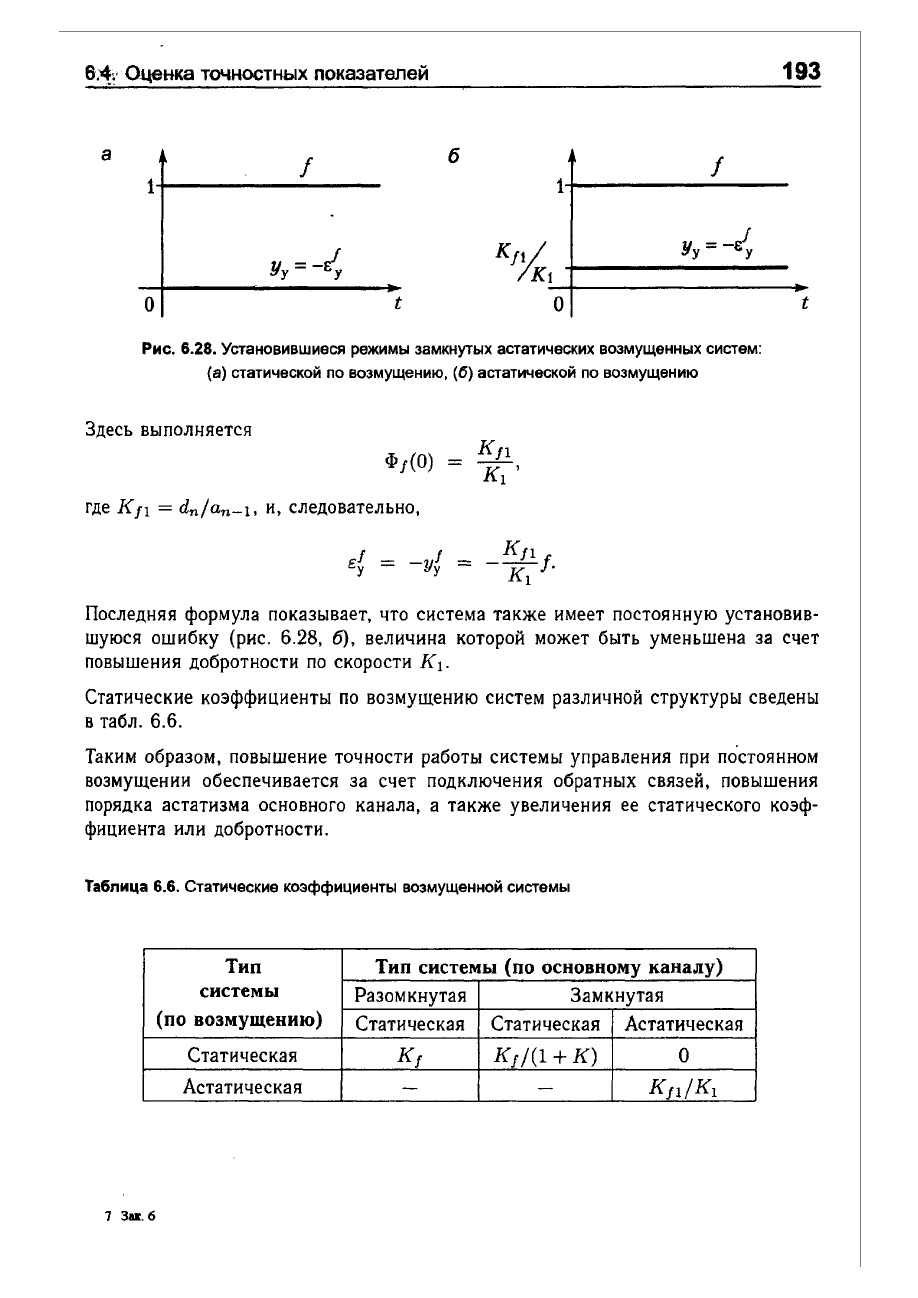
Рис.
6.28.
Установивwиеся
режимы
замкнутых
астатических
возмущенных
систем:
(8)
статической
по
возмущению,
(6)
астатической
по
возмущению
Здесь
выполняется
где
K!l
=
dn/an-l.
и,
следовательно,
со!
_
_у!
= _
к
f1 f
Су
-
у
K
1
'
193
t
Последняя
формула
показывает,
что
система
также
имеет
постоянную
установив
шуюся
ошибку
(рис.
6.28,
6),
величина
которой
может
быть
уменьшена
за
счет
повышения
добротности
по
скорости
К
1.
Статические
коэффициенты
по
возмущению
систем
различной
структуры
сведены
в
табл.
6.6.
Таким
образом,
повышение
точности
работы
системы
управления
при
по'стоянном
возмущении
обеспечивается
за
счет
подключения
обратных
связей,
повышения
порядка
астатизма
основного
канала,
а
также
увеличения
ее
статического
коэф
фициента
или
добротности.
Таблица
6.6.
Статические
коэффициенты
возмущенной
системы
7
3В.6
Тип
системы
(по
возмущению)
Статическая
Астатическая
Тип
системы
(по
основному
каналу)
Разомкнутая
Замкнутая
Статическая Статическая
Астатическая

194
Глава
6.
Качество
систем
управле~я'
6.4.4.
Оценка
точности
в
типовых
режимах
и
метод
коэффициентов
ошибок
Рассмотрим
поведение
невозмущенной
замкнутой
системы
y(t) =
Ф(р)
у*и)
(6.105)
для
различных
типов
задающих
воздействий
y*(t).
В
общем
случае
достаточно
гладкая
функция
времени
представима
в
виде
бесконечного
ряда
(ряда
Тейлора)
y*(t) =
y~+yit+Y2t2+
...
,
где
У;
(t) =
у*
(O)/i! -
постоянные
коэффициенты.
В
зависимости
от
значений
у;
различают
следующие
типовые
режимы:
•
стационарный
режим
(режим
стабилизации),
для
которого
у*
=
уа;
•
режим
движения
с
постоянной
скоростью,
для
которого
у*
=
Vot
и
V
o
-
скорость
движения;
•
режим
движения
с
постоянным
ускорением,
для
которого
у*
=
aot
2
/2
и
ао
-
ускорение.
Для
оценки
точности
замкнутых
систем
вводятся
коэффициенты
ошибок
(чув
ст8ител~ности
)
W(p) I ' W'(p) I
Ф
О
=
Ф(О)
= 1 + W(p)
р=о;
Ф
1
=
Ф
(О)
=
(1
+ W(p))2
р=о;
Ф2
=
Ф"(О)
=
W"(p)(~
+
W~)~r
2W'(p) I
и
т.
Д.,
1 +
р
р=о
где
штрихом
отмечена операция
дифференцирования
по
р
.
Установившаяся
со
ставляющая
выходной
переменной
определяется
выражением
(рис.
6.29)
(t)
Ф
*
ф'*
Ф2
""*
Уу
=
оу
+
lУ
+
2Т
У
+ ... ,
а
установившаяся
ошибка
-
ey(t) =
(1
-
Фо)У*
-
ФIУ*
-
~~
у*
-
....
Коэффициенты
чувствительности
вычисляются
через
статические
коэффициенты
и
добротности
системы
(К,
К
1
,
К
2
И
Т.
д.,
см.
6.4.2).
Формулы
для
расчета
неко
торых
значений
Фi
для
основных
типов
замкнутых
систем
приведены
в
табл.
6.7.

6.:4.
_OЦ~HKa
T~HOCTHЫX
показателей
195
у*
1
У
у
Рис.
6.29.
Схема
определения
установившейся
составляющей
Таблица
6.7.
Коэффициенты
ошибок
(чувствительности)
ПОРЯДОК
астатизма
Ф
О
Ф
1
Ф
2
/2!
О
К/(l
+
К)
-
-
1 1
-1/К
1
-
2 1
О
-1/К
2
в
стационарном
режиме
имеет
место
зависимость
Уу
=
ФоУ*.
Абсолютная
точность
и
Е:
у
=
О
достигается
при
Ф
О
=
1,
что
выполняется
только
для
астатических
систем.
Для
статической
системы
1 *
Е:
у
= 1 +
К
У
,
и
система
имеет
постоянную
установившуюся
ошибку,
которая
может
быть
умень
шена
за
счет
увеличения
коэффициента
К.
В
режиме
движения
с
постоянной
скоростью
V
o
имеет
место
Абсолютная
точность
достигается
при
Ф
О
= 1
и
Ф
1
=
О,
что
выполняется
для
систем
с
порядком
астатизма
2
и
выше.
В
системе
с
астатизмом
l-го
порядка
возникает
постоянная
установившаяся
ошибка
1
Е:
у
=
1<1
V
o
,
которая
может
быть
уменьшена
за
счет
увеличения
коэффициента
(добротности
по
скорости)
К
1
,
а
в
статической
системе
с
течением
времени
ошибка
неограниченно
нарастает.

196
Глава
6.
Качество
систем
управления
в
режи'м'е
движения
с
nостоянны'м'
ускорение'м'
ао
имеет
место
Абсолютная
точность
достигается
при
ФО
= 1
и
Фl
=
Ф2
=
О,
что
выполняется
для
астатических систем
порядка
3
и
выше.
В
системе
с
астатизмом
2-го
порядка
возникает
постоянная
установившаяся
ошибка
Таким
образом,
повышение
точности
систем
автоматического
управления
достига
ется:
•
подключением
обратных
связей
(замыканием
системы);
•
повышением
порядка
астатизма основного
канала
с
помощью
соответствую
щих
регуляторов (алгоритмов
управления);
•
повышением
добротности
системы
за
счет
увеличения
коэффициентов
регу
лятора.

Глава
7.
Методы
управления
и
синтез
еДУ
Системы
автоматического
управления
предназначены
для
стабилизации,
слежения
и
решения
других
задач
управления
динамическими
процессами
(см.
п.
1.4),
что
предусматривает
поддержание
желаемых
законов
изменения
регулируемых
пере
менных
y(t)
или
переменных
состояния
Xi(t)
с
заданными
показателями
качества.
Управление,
обеспечивающее
решение
указанных
задач,
осуществляется
с
помо
щью
регуляторов,
задающих
блоков
или
иных
элементов
САУ.
В
этом
разделе
рассматриваются
общие
подходы
к
проблемам
стабилизации,
слежения
и
наблюде
ния,
изучаются
некоторые
классические
и
современные
методы
построения
(синте
за)
различных
типов
систем
управления
выходом
и
состоянием
линейных
объектов
(см.
также
[1,
2,
3,
10]
и
др.).
7.1.
Общие
принципы
управления
С
помощью
регуляторов
в
систему
управления
вводятся
контуры
(каналы)
прямых
и
обратных
связей.
В
зависимости
от
структуры
связей
имеет
место
классификация
стратегий
и
принципов
управления,
приведенная
на
рис.
7.1.
Управление
Рис.
7.1.
Принципы
управления

198
Глава
7.
Методы
управления
и
синтез
еду
Формулировка
локальных
задач
стабилизации
и
слежения
в
традиционной
поста
новке
(см.
1.4.1)
приводит
к
концепции
управления
по
выходу
ОУ
и
простейшей
(<классической»)
структуре
САУ,
содержащей
контуры
прямых
связей
по
задаю
щему
воздействию
у* и
обратных
связей
по
выходу
у.
В
зависимости
от
структуры
связей
различают
разомкнутое,
замкнутое
и
комбинированное
управление.
По
следние
два
типа
предусматривают
коррекцию
поведения
системы
в
зависимости
от
рассогласования
у*
-
у,
что
требует
формиров-ания
обратных
связей.
у*
и
У
~
Разомкнутое
управление
вводит
в
состав
системы
контур
прямой
связи
по
задающему
воздействию:
u =
U(у*),
где
u(·)
-
функциональный
оператор,
который
должен
выбираться
из
условия
получения
заданного
закона
изменения
выходной
переменной
ОУ,
т.
е.
условия
у
= y*(t).
При
этом
текущее
поведение
объекта
не
контролируется.
Пример
7.1.
Рассмотрим
объект
второго
порядка
Ко
(7.1)
Выберем
управление
(контур
прямой
связи)
вида
u =
lзу*
+
l2i/
+ llY* =
(lз
+
[2Р
+
llp
2
)y,
(7.2)
где
11,
l2,
lз
-
постоянные
коэффициенты,
назначаемые
как
l
1 l
Т
1
+
Т
2
l
1 =
Ко'
2 =
КО
' 3
После
подстановки
(7.2)
в
(7.1)
получаем
модель
системы
управления
у
=
у.,
что
указывает
на
достижение
абсолютной
точности
слежения.
о
Отличие
свойств
реального
объекта
от
его
математической
модели,
используемой
при
построении
алгоритма
разомкнутого
управления,
и
влияние
возмущений
как
правило
не
позволяют
обеспечить
требуемой
идентичности
выходной
переменной
y(t)
и
задающего
воздействия
y*(t).
Более
того,
прямые
связи
обычно
содержат
операции
дифференцирования,
что
усложняет
их
практическую
реализацию.
И
на
конец,
возможная
неустойчивость
ОУ
приводит
к
получению
нера60тосnосо6ной
разомкнутой
системы
управления.
Пример
7.2.
Рассмотрим
объект
второго
порядка
(см.
пример
2.7)
КО
у
=
2
и
,
р
(7.3)
7.1'.
Общие
ПРИНЦИПЫ
управления
199
Контур
прямой
связи,
выбираемый
из
условия
получения
абсолютной
точности
слежения,
описывается
выражением
1
..
*
и =
-у
ко
После
подстановки
в
(7.3)
получаем
р2
*
у
=
р2
У
.
(7.4)
Сокращение
числителя
и
знаменателя
приводит
к
тождеству
у
=
у*,
что
указы
вает
на
достижение
абсолютной
точности.
Однако
характеристическое
уравнение
системы
(7.4)
р2
=
О
имеет
два
нулевых
корня.
Поэтому
полученная
система
неустойчива
и
неработоспособна.
О
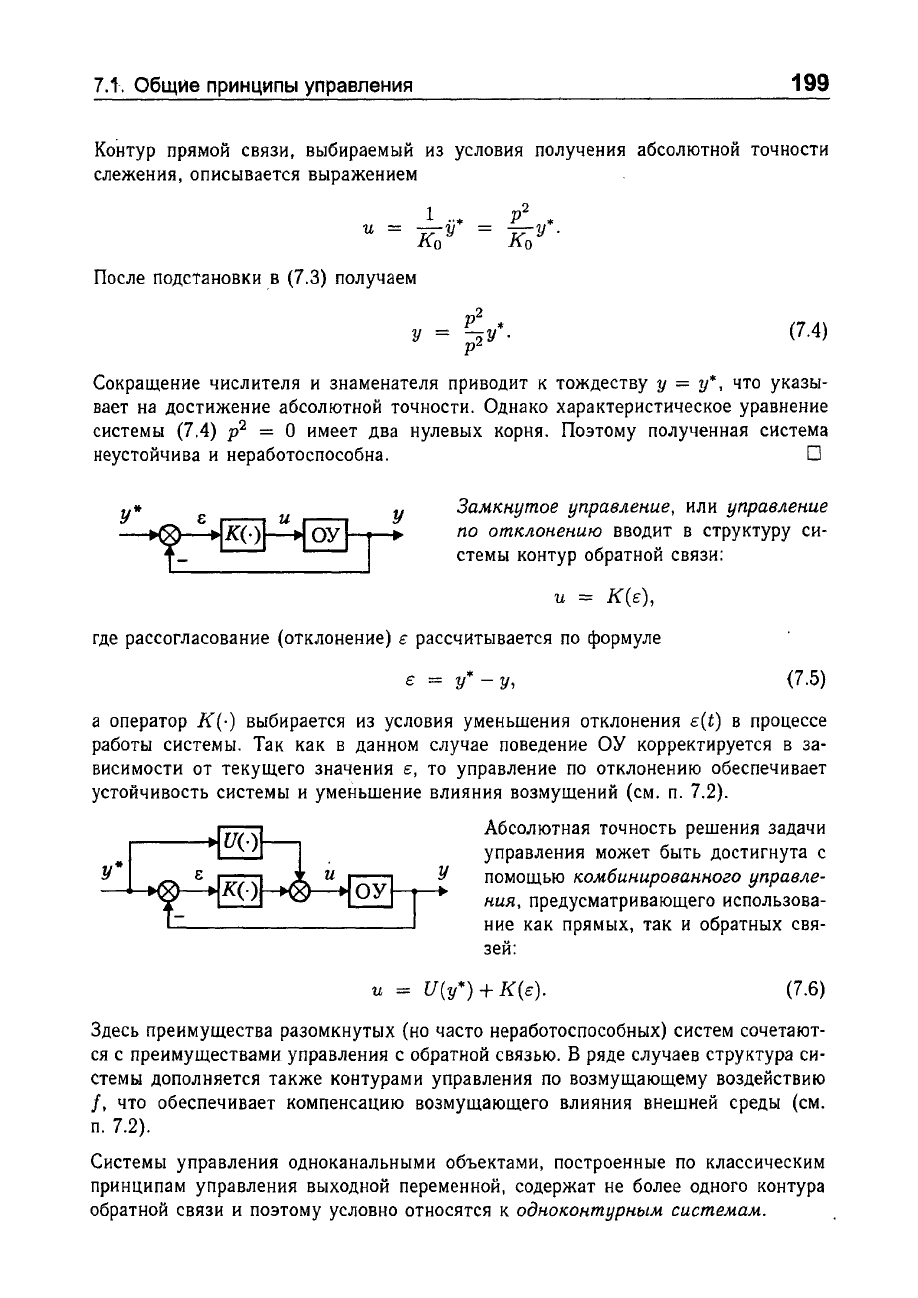
Замкнутое
управление,
или
управление
по
отклонению
вводит
в
структуру
си
стемы
контур обратной
связи:
и
=
К(е),
где
рассогласование
(отклонение)
е
рассчитывается
по
формуле
е
=
у*
-
у,
(7.5)
а
оператор
к(·)
выбирается
из
условия
уменьшения
отклонения
e(t)
в
процессе
работы
системы.
Так
как
в
данном
случае
поведение
аУ
корректируется
в
за
висимости
от
текущего
значения
е,
то
управление
по
отклонению
обеспечивает
устойчивость
системы
и
уменьшение
влияния
возмущений
(см.
п.
7.2).
у*
& U
У
~
Абсолютная
точность
решения
задачи
управления
может
быть
достигнута
с
помощью
комбинированного
управле
НИЯ,
предусматривающего
использова
ние как
прямых,
так
и
обратных
свя
зей:
и
=
U(у*)
+
К(е).
(7.6)
Здесь
преимущества
разомкнутых
(но
часто
неработоспособных)
систем
сочетают
ся
с
преимуществами
управления
с
обратной
связью.
В
ряде
случаев
структура
си
стемы
дополняется
также
контурами
управления
по
возмущающему
воздействию
f.
что
обеспечивает
компенсацию
возмущающего
влияния
внешней
среды
(см.
п.7.2).
Системы
управления
одноканальными
объектами,
построенные
по
классическим
принципам
управления
выходной
переменной,
содержат
не
более
одного
контура
обратной
связи
и
поэтому
условно
относятся
к
одноконтурным
системам.
