Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.


200
Глава
7.
Методы
управления
и
синтез
еДУ
Подключение
дополнительных
контуров
прямой
и
обратной
связи
в
многоконтур
ных
системах
обеспечивает
повышение
качества
управления.
Наиболее
полная
информация
об
управляемом
процессе
содержится
в
переменных
состояния
(см.
3.1.1),
и
поэтому
управление
по
состоянию
позволяет
достичь
наилучших
каче
ственных
показателей
системы.
При
управлении
по
состоянию
(см.
п.
7.3)
различа
ют
замкнутые
алгоритмы
управления
(контуры
обратных
связей по отклонению):
и
= I«(e),
где
вектор
отклонений
(рассогласований)
е
часто
рассчитывается
по
простой
фор
муле
е
=
х*
-
х,
и
алгоритмы
комбинированного
типа:
и
=
U(х*)
+
К(е),
содержащие
также
контуры
прямых
связей
по
задающему
воздействию
x*(t).
В
тех
случаях,
когда
в
САУ
измеряется
только
выходная
переменная
у,
для
реа
лизации
управления
по
состоянию
требуется
построение
дополнительных
динами
ческих
элементов
-
наблюдателей,
предназначенных
для
оценивания
всех
пере
менных
состояния
системы
(см.
1.5.3
и
п.
7.4).
При
этом
в
алгоритмах
управления
состоянием
вместо
вектора
х
используется
полученная
с
помощью
наблюдателя
оцен-ка
состояния
Х.
Динамическое
устройство
управления,
в
состав
которого
вхо
дит
наблюдатель,
приобретает
форму
регулятора
выхода
(см.
п.
7.5).
Основным
функциональным
элементом
устройства
управления
САУ
является
ре
гулятор.
В
соответствии
с
рассмотренными
принципами
управления
(см.
рис.
7.1)
различают
регуляторы
выхода
и
состояния,
разомкнутые
регуляторы
и
регулято
ры
комбинированного
типа.
В
зависимости
от
типов
функциональных
операторов
U(·)
и
к(·),
встречающихся
в
рассмотренных
алгоритмах
управления,
различают
следующие
основные
типы
регуляторов:
•
динамические
и
статические;
•
линейные
инелинейные.
к
динамическим
относится
большинство
стандартных
регуляторов
одноконтур
ных
систем
(см.
п.
7.2),
регуляторы
состояния
астатического
типа
(см.
7.3.2
и
7.3.3)
и
регуляторы
с
наблюдателями
состояния объекта
или
внешней
среды
(см.
п.
7.5).
Характерной
особенностью
нелинейных
регуляторов
является
ис
пользование
элементов
с
нелинейной
(например,
релейной)
характеристикой
[3,
4,
22,
26,
27,
30,
34,
36,
41,
46).
Дальнейшее
изложение
касается
только
линейных
регуляторов
статического
и
динамического
типа.
7.2.
Управление
выходом
и
одноконтурные
системы
201
7.2.
Управление
выходом
и
одноконтурные
системы
Устройство
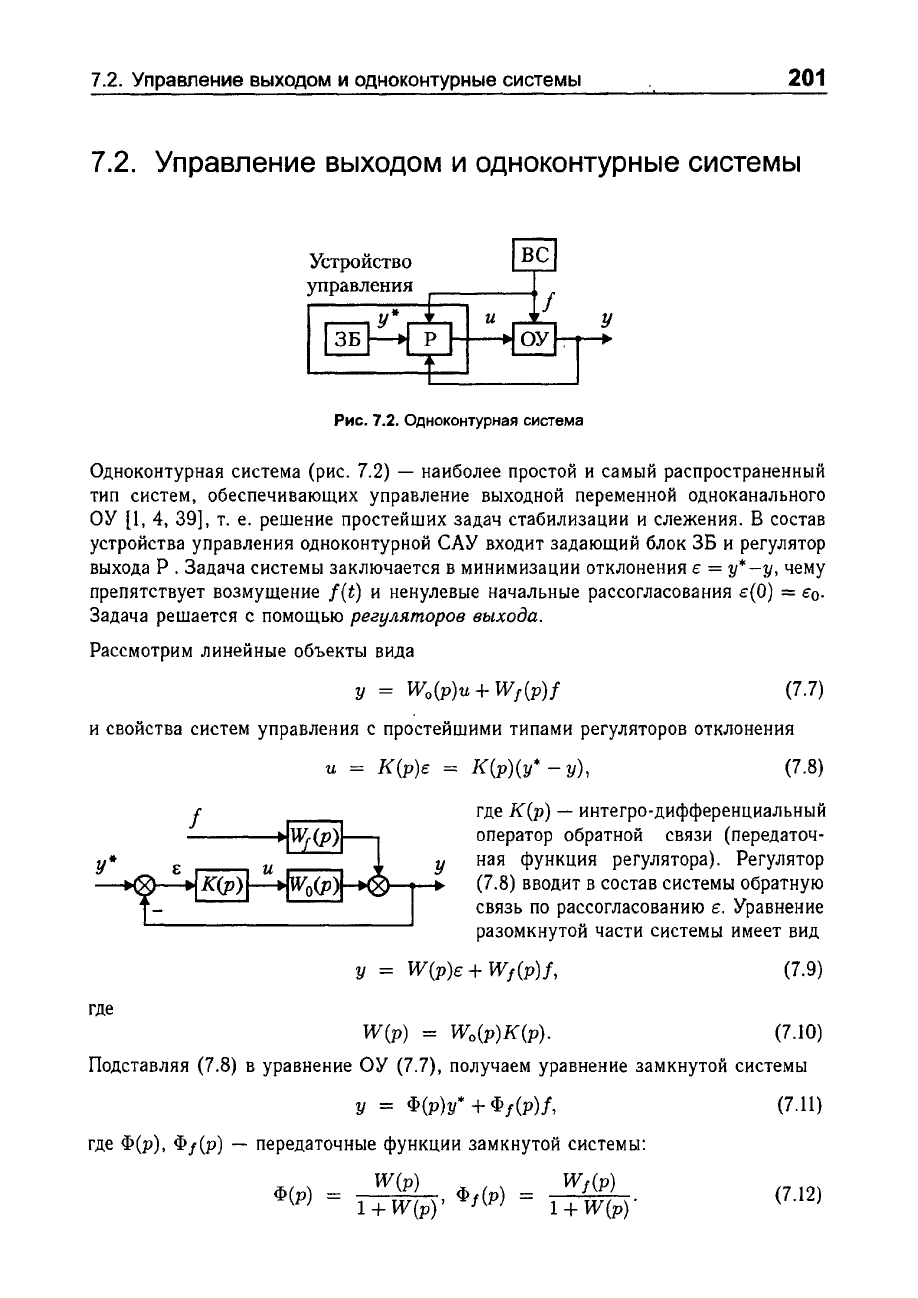
Рис.
7.2.
Одноконтурная
система
Одноконтурная
система
(рис.
7.2)
-
наиболее
простой
и
самый
распространенный
тип
систем,
обеспечивающих
управление
выходной
переменной
одноканального
ОУ
[1,
4,
39],
т.
е.
решение
простейших
задач
стабилизации
и
слежения.
В
состав
устройства
управления
одноконтурной
САУ
входит
задающий
блок
ЗБ
и
регулятор
выхода
Р
.
Задача
системы
заключается
в
минимизации
отклонения
€ =
у*
-у,
чему
препятствует
возмущение
f(t)
и
ненулевые
начальные
рассогласования
€(O)
=
€o.
Задача
решается
с
помощью
регуляторов
выхода.
Рассмотрим
линейные
объекты
вида
(7.7)
и
свойства
систем
управления
с
простейшими
типами
регуляторов
отклонения
и
= K(p)€ =
К(р)(у*
-
у),
(7.8)
у*
Е
U
У
~
где
К(р)
-
интегро-дифференциальный
оператор
обратной
связи
(передаточ
ная
функция
регулятора).
Регулятор
(7.8)
вводит
в
состав
системы
обратную
связь
по
рассогласованию
€.
Уравнение
разомкнутой
части
системы
имеет
вид
(7.9)
где
W(p) = Wo(p)K(p).
(7.10)
Подставляя
(7.8)
в
уравнение
ОУ
(7.7),
получаем
уравнение
замкнутой системы
у
=
Ф(р)у*
+
Фf(р)f,
(7.11)
где
Ф(р),
Фf(Р)
-
передаточные
функции
замкнутой
системы:
W(p) Wf(p)
Ф(р)
= 1 + W(p) ,
Фf(Р)
= 1 +
W(p)'
(7.12)

202
Гл~ва
7.
Методы
управления
14
синтез
САУ
Подставив
(7.11)
в
уравнение
(7.5),
нетрудно
получить
модель
ошибки
слежения
(7.13)
где
Ф€(р)
-
передаточная
функция
замкнутой
системы
по
ошибке
слежения:
(7.14)
Напомним,
что
замыкание
системы
приводит
к
изменению
ее
передаточной
функ
ции
(ср.
выражения
(7.10)
и
'(7.12),
(7.14»,
характеристического
полинома,
а
сле
довательно,
динамических
и
точностных
показателей
(см.
п.
4.3
и
главу
6).
В
зависимости
от
конкретной
реализации
оператора
К(р)
различают
пропор
циональные
(П),
пропорционально-дифференциальные
(ПД),
пропорционально
интегральные
(ПИ)
и
пропорционально-интегрально-дифференциальные
(ПИД)
регуляторы
выхода.
П-регулятор.
Регулятор
этого
типа
описывается
алгебраическим
уравнением:
(7.15)
где
К
р
>
О
-
постоянный
коэффициент
обратной
связи.
Значение
К
р
выбирается
таким
образом,
чтобы
уменьшить
величину
отклонения
Е,
вызванного
действием
возмущения
f(t),
начальным
рассогласованием
Ео
и,
возможно,
выIокимM
темпом
изменения
задающего
воздействия
y*(t).
Увеличение
К
р
обычно
обеспечивает
сни
жение
ошибки,
но
приводит
к
ухудшению
динамических
свойств
системы
-
по
вышению
ко.1Iебательности.
Поэтому
задача
выбора
коэффициента
обратной
связи
решается
компромиссным
образом.
При.мер
7.3.
Рассмотрим
возмущенный
объект
второго
порядка
(см.
при
мер
2.3
и
4.1.3)
Ко
К!
f
у
=
и
+
---=:...--
р(Тр
+ 1)
р(Тр
+ 1)
(7.l6)
с
передаточными
функциями
(
КО
К!
W
o
р)
=
р(Тр
+
1)'
Wj(p)
=
р(Тр
+
1)'
где
Ко
>
О.
Передаточные
функции
замкнутой
системы
сП-регулятором
(7.15)
принимают
вид
Ф(р)
Полюсы
системы
-
1
/1-
4К
о
К
р
Рl,2
= -
2Т
±
2Т
'
и
поэтому
система
асимптотически
устойчива.

7.2.
Управление
ВЫХОДОМ
и
одноконтурные
системы
а
б
у*
о
t
о
Рис.
7.3.
Переходные
процессы
системы
с
П-регулятором
(пример
7.3)
при
постоянном
(а)
и
линейно
нарастающем
(6)
эадающем
ВОЗДействии
203
t
Рассмотрим
невозмущенную
систему,
полагая
f =
о.
Передаточная
функция
по
ошибке
t
принимает
вид
Значение
установившейся
ошибки
при
постоянном
задающем
воздействии
опреде-
ляется
выражением
(7.17)
т.
е.
при
у*
= const
система
обеспечивает
абсолютную
точность
(рис.7.3,
а).
Это
объясняется
наличием
астатических
свойств
ОУ
и,
следовательно,
основного
ка
нала
системы
(см.
п.
6.4).
Для
линейно
нарастающего
сигнала
y*(t)
=
V*t,
где
V* = const,
система
имеет
постоянную
ошибку,
величина
которой обратно
пропор
циональна
коэффициенту
К
р
(рис.
7.3,
б)
,
причем
при
увеличении
К
р
повышается
колебательность
процессов.
В
присутствии
возмущений
система
также
имеет
ненулевую
установившуюся
ошибку
f
К!
€y
=
-Фf(О)j
= -
КоК
р
j,
величина
которой
может
быть
уменьшена
за
счет
увеличения
коэффициента
регу
лятора
К
р
(рис.
7.4).
О
Отметим,
что
системы
с
пропорциональным
регулятором
во
многих
случаях
не
обладают
свойством
асимптотической
устойчивости
и
поэтому
неработоспособны
(см.
пример
7.4). .
ОД-регулятор.
Для
улучшения
динамических
свойств
САУ
(достижения
асимп
тотической
устойчивости,
снижения
колебательности
процессов)
в
закон
управ
ления
вводят
производные
от
отклонения
Е:.
Тем
самым
формируется
алгоритм
ПД
-регулятора:
и
=
КрЕ:
+ KD€ =
(К
р
+ KDP)€,
т.
е.
регулятора
с
передаточной
функцией
К(р)
=
К
р
+ KDP,
(7.18)
204
о
Глава
7.
Методы
управления
и
синтез
еду
у*
к
= 1
р
2
10
t
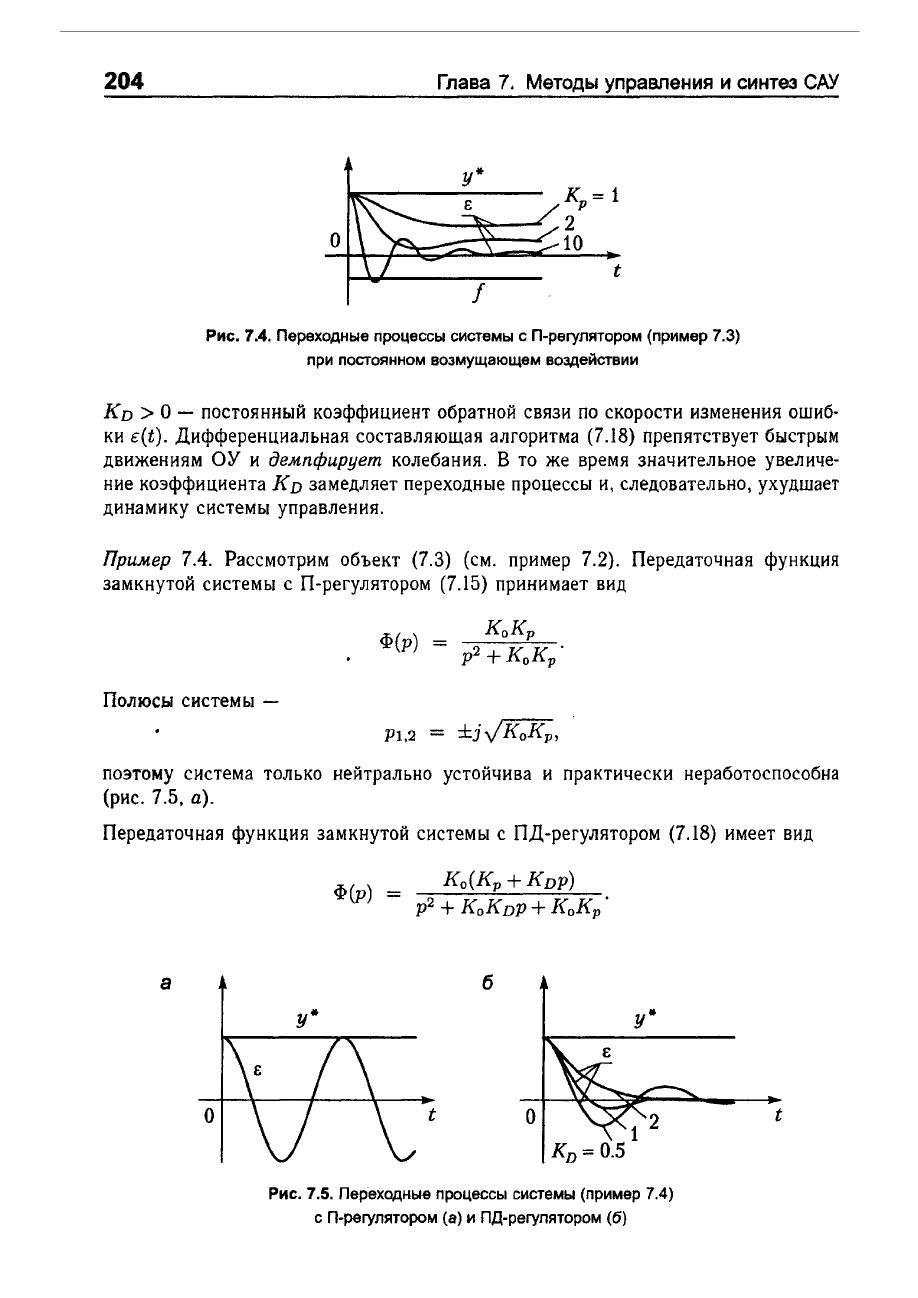
Рис.
7.4.
Переходные
процессы
системы
сП-регулятором
(пример
7.3)
при
постоянном
возмущающем
воздействии
KD >
о
-
постоянный
коэффициент
обратной
связи
по
скорости
изменения
ошиб
ки
e(t).
Дифференциальная
составляющая
алгоритма
(7.18)
препятствует
быстрым
движениям
ОУ
и
демnфuрует
колебания.
В
то
же
время
значительное
увеличе
ние
коэффициента
KD
замедляет
переходные
процессы
и,
следовательно,
ухудшает
динамику
системы
управления.
Прuмер
7.4.
Рассмотрим
объект
(7.3)
(см.
при
мер
7.2).
Передаточная
функция
замкнутой
системы
с
П-регулятором
(7.15)
принимает
вид
(
КоКр
Ф
р)
= 2
К
К
.
Р
+
о
р
Полюсы
системы
-
Рl,2
=
±j.jKoK
p
,
поэтому
система
только
нейтрально
устойчива
и
практически
неработоспособна
(рис.
7.5,
а).
Передаточная
функция
замкнутой
системы
с
ПД-регулятором
(7.18)
имеет
вид
а
о
б
у*
у*
t
о
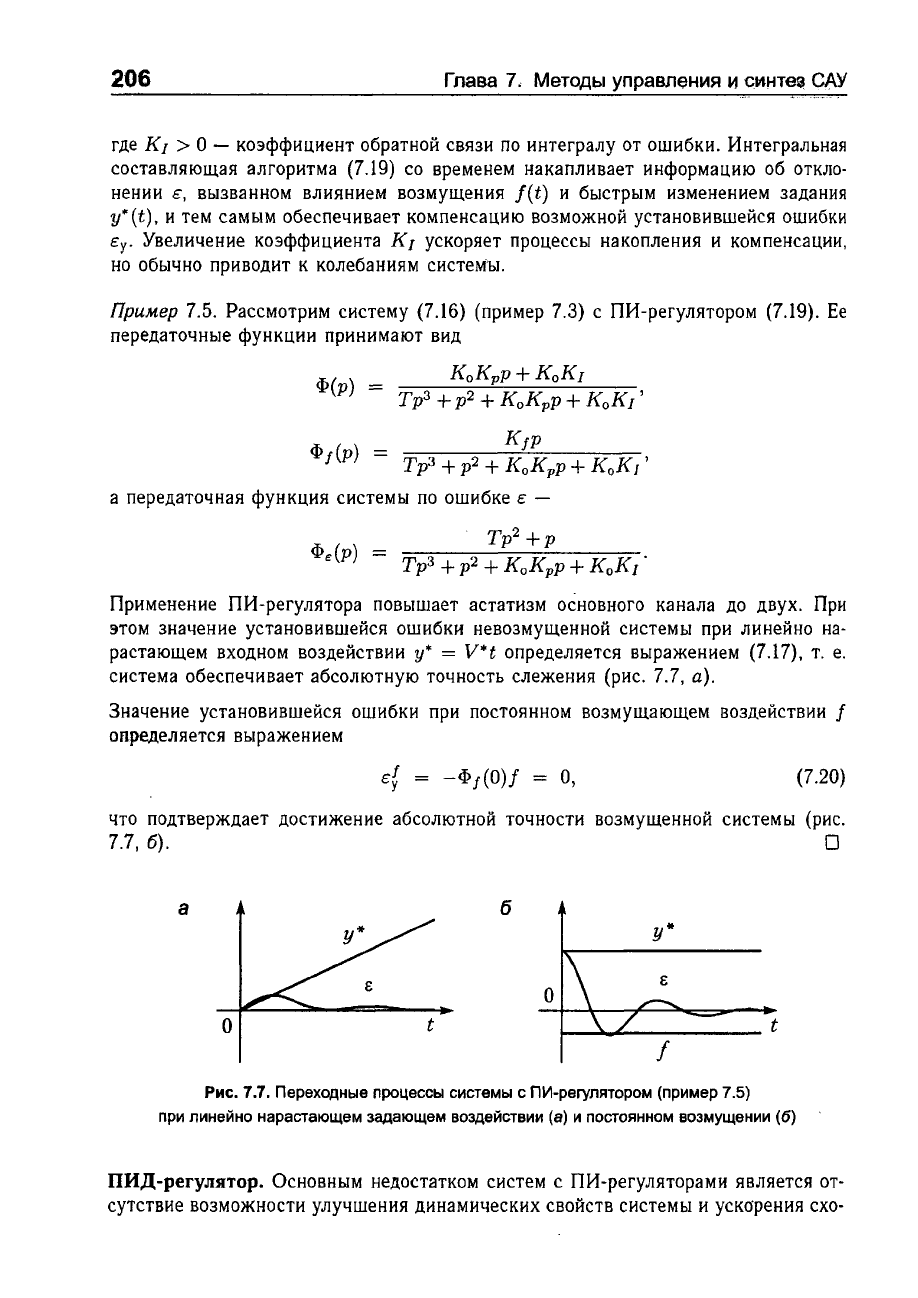
Рис.
7.5.
Пер"еходные
процессы
системы
(пример
7.4)
с
П-регулятором
(а)
и
ПД-регулятором
(6)
t

7.2.
Управление
выходом
и
одноконтурные
системы
205
Полюсы
системы
к
к
.
/K;K~
-
4K
o
K
v
Рl,2
=
_~±",""Y
______
_
2 2
имеют
отрицательную
вещественную
часть,
и
полученная
система
асимптотически
устойчива.
При
этом
увеличение
коэффициента
KD
обеспечивает
демпфирование
системы
-
уменьщение
колебательности
переходных
процессов
(рис.
7.5,
б).
Более
того,
за
счет
выбора
коэффициентов
К
р
и
KD
можно
получить
любые
значения
основных
коэффициентов
характеристического
полинома
(знаменателя
передаточ
ной
функции)
и,
следовательно,
требуемые
значения
полюсов
замкнутой
системы,
что
позволяет
обеспечить
любые
желаемые
динамические
свойства.
Передаточная
функция
системы
по
ошибке
е
принимает
вид
Значение
установившейся
ошибки
при
постоянном
входном
воздействии
у*
опреде
ляется
выражением
(7.17),
т.
е.
при
у*
= const
система
обеспечивает
абсолютную
точность
слежения.
Отметим,
что
в
силу
астатизма
второго
порядка
(основного
контура)
система
имеет
абсолютную
точность
и
при
линейно
нарастающих
8Хо.в.
ных
воздействиях
у*
=
V*t
(рис.
7.6).
О
о
t
Рис.
7.6.
Переходные
процессы
системы
с
ПД-регулятором
(пример
7.4)
при
линейно
нарастающем
задающем
воздействии
ПИ-регулятор.
В
общем
случае
повышение
точности
САУ
(снижение
установив
шейся
ошибки
е)
достигается
при
повышении
коэффициентов
П-,.И'
ПД-регуляторов
либо
за
счет
увеличения
астатизма
основного
канала
системы.
Последнее
обеспе
чивается
с
помощью
ПИ-регулятора:
и
=
КР"+КI
l'
"dr
=
передаточная
функция
которого
имеет
вид
(7.19)
206
Глава
7;
Методы
управления
и синте~
едУ
где
К]
>
О
-
коэффициент
обратной
связи
по
интегралу
от
ошибки.
Интегральная
составляющая
алгоритма
(7.19)
со
временем
накапливает
информацию
об
откло
нении
е,
вызванном
влиянием
возмущения
f(t)
и
быстрым
изменением
задания
y*(t),
и
тем
самым
обеспечивает
компенсацию
возможной
установившейся
ошибки
€Y'
Увеличение
коэффициента
К]
ускоряет
процессы
накопления
и
компенсации,
но
обычно
приводит
к
колебаниям
системы.
Прuмер
7.5.
Рассмотрим
систему
(7.16)
(при
мер
7.3)
сПИ-регулятором
(7.19).
Ее
передаточные
функции
принимают
вид
(
КоКрР
+
КоК]
Ф
Р)
=
Тр3
+
р2
+
КоКрР
+
КоК]'
KJp
ФJ(Р)
=
Тр3
+
р
2
+
КоКрР
+
КоК]'
а
передаточная
функция
системы
по
ошибке
€ -
Тр
2
+р
=
Тр
3
+
р
2
+
КоКрР
+
КОК]
.
Фе(Р)
Применение
ПИ-регулятора
повышает
астатизм
основного
канала
до
двух.
При
этом
значение
установившейся
ошибки
невозмущенной
системы
при
линейно
на
растающем
входном
воздействии
у*
=
V*t
определяется
выражением
(7.17),
т.
е.
система
обеспечивает
абсолютную
точность
слежения
(рис.
7.7,
а).
Значение
установившейся
ошибки
при
постоянном
возмущающем
воздействии
f
определяется
выражением
(7.20)
что
подтверждает
достижение
абсолютной
точности
возмущенной
системы
(рис.
7.7,
б).
О
а
б
у*
о
о
t
I--......Jo,~------
t
f
Рис.
7.7.
Переходные
процессы
системы
сПИ-регулятором
(пример
7.S)
при
линейно
нарастающем
задающем
воздействии
(а)
и
постоянном
возмущении
(б)
ПИД-регулятор.
Основным
недостатком
систем
с
ПИ-регуляторами
является
от
сутствие
возможности
улучшения
динамических
свойств
системы
и
ускорения
схо-

7~2.
Управление
выходом
и
одноконтурные
системы
207
димости
процессов.
Увеличение
коэффициентов
К
р
и
К!
обычно
при
водит
к
ко
лебательным
процессам
(см.
рис.
7.7).
Одновременное
улучшение
динамических
свойств
и
точности
САУ
обеспечивается
ПИД-регулятором:
и
=
Kpe+KDE+K[
l'
edr
=
с
передаточной
функцией
К(р)
= K
D
p
2
+
КрР
+
К[
р
(7.21)
а
также
более
сложными
типами
линейных
динамических
регуляторов
выхода
(7.8).
Прuм,ер
7.6.
Рассмотрим
возмущенный
объект
второго
порядка
(см.
примеры
2.6,
7.2
и
7.4):
(7.22)
для
которого
Wf(p) =
К/.
Р
При
использовании
ПД
-регулятора
получаем
и,
следовательно,
Повышение
точности,
в
принципе,
может
быть
достигнуто
за
счет
увеличения
коэффициента
К
р
,
что,
однако,
приводит
к
усилению
колебательности
системы
(рис.
7.8,
а).
С
другой
стороны,
нетрудно
показать,
что
для
такого
объекта
си
стема
с
ПИ-регулятором
оказывается
неустоЙчивоЙ.
Наилучшее
решение
преду
сматривает
использование
положительных
свойств
ПД-
и
ПИ-регуляторов,
т.
е.
подключение
ПИД
-регулятора.
Передаточные
функции
замкнутой
системы
сПИД-регулятором
(7.21)
имеют
вид
Ф(
) = K
o
KDp
2
+
КоКрР
+
кок
!
Р
р3
+ K
o
K
D
p
2
+
КоКрР
+
КоК
!
'
Kfp
Фf(Р)
= 3
К
К
2
К
К
К
К
.
р
+
о
DP
+
о
рР
+
о
1
Значения
коэффициентов
характеристического
полинома
замкнутой
системы
(зна
менателя
передаточной
функции
Ф(р»
полностью
определяются
выбором
трех
ко
эффициентов
регулятора
К
р
,
KD,
К!
И
обеспечивают
любую
требуемую
динамику
208
а
О
Глава
7.
Методы
управления
и
синтез
еДУ
б
у*
у*
К
= 1
р
2
О
10
t
f f
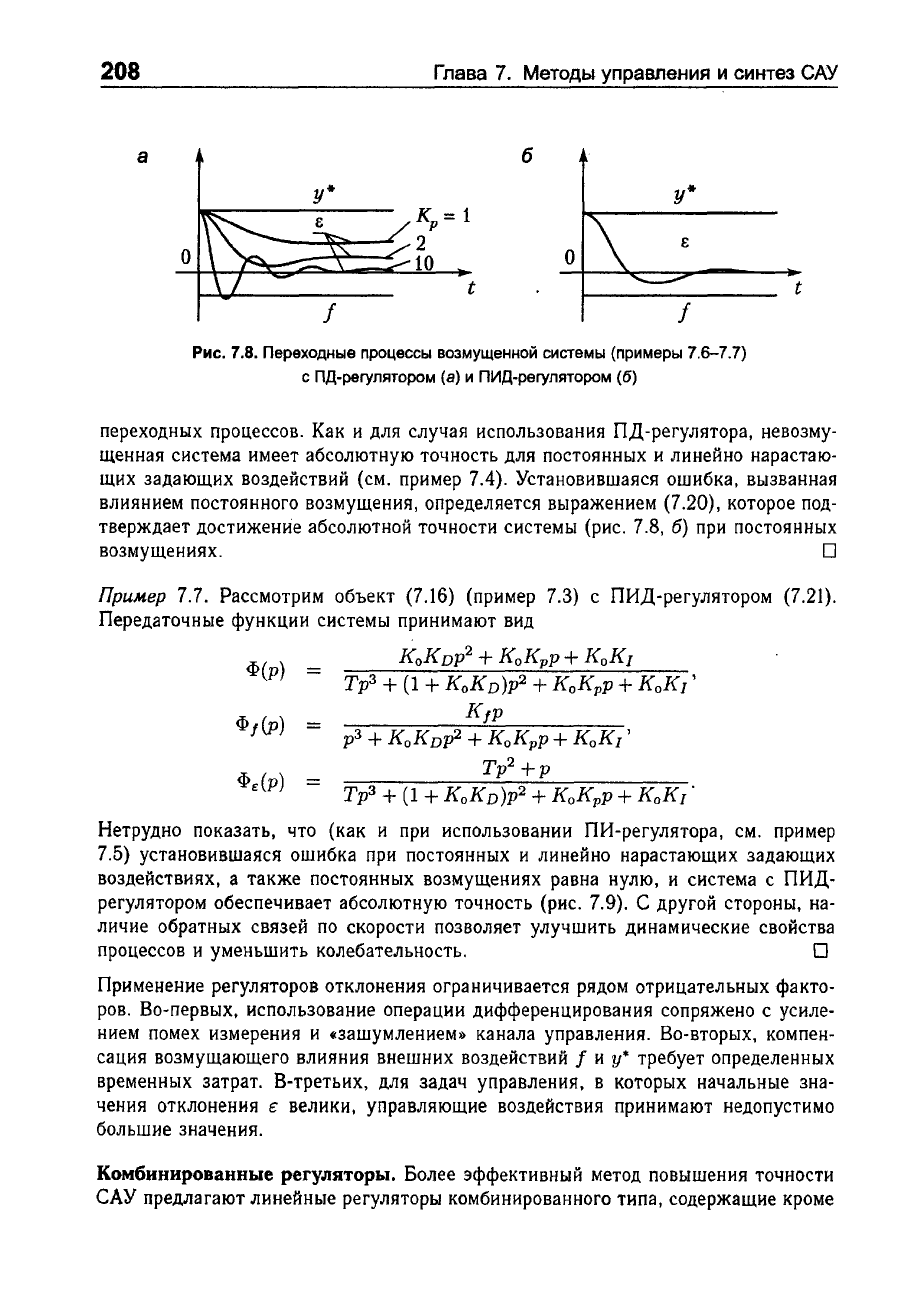
Рис.
7.8.
Переходные
процессы
возмущенной
системы
(при
меры
7.6-7.7)
с
ПД-регулятором
(а)
и
ПИД-регулятором
(6)
t
переходных
процессов.
Как
и
для
случая
использования
ПД
-регулятора,
невозму
щенная
система
имеет
абсолютную
точность
для
постоянных
и
линейно
нарастаю
щих
задающих
воздействий
(см.
при
мер
7.4).
Установившаяся
ошибка,
вызванная
влиянием
постоянного
возмущения,
определяется
выражением
(7.20),
которое
под
тверждает
достижение
абсолютной
точности
системы
(рис.
7.8,
б)
при
постоянных
возмущениях.
О
Прuмер
7.7.
Рассмотрим
объект
(7.16)
(пример
7.3)
сПИД-регулятором
(7.21).
Передаточные
функции
системы
принимают
вид
K
o
KDp
2
+
КоКрР
+
КоК!
Ф(р)
=
Тр
3
+
(1
+ K
o
KD)p
2
+
КоКрР+
KoKI'
Фf(Р)
=
Kfp
р
3
+ K
o
K
D
p
2
+
КоКрР
+
КоК!
'
Тр
2
+р
ФЕ(р)
=
Тр
3
+
(1
+ K
o
KD)p
2
+
КоКрР
+
KoKI'
Нетрудно
показать,
что
(как
и
при
использовании
ПИ-регулятора,
см.
при
мер
7.5)
установившаяся
ошибка
при
постоянных
и
линейно
нарастающих
задающих
воздействиях,
а
также
постоянных
возмущениях
равна
нулю,
и
система
с
ПИД
регулятором
обеспечивает
абсолютную
точность
(рис.
7.9).
С
другой
стороны,
на
личие
обратных
связей
по
скорости
позволяет
улучшить
динамические
свойства
процессов
и
уменьшить
колебательность.
О
Применение
регуляторов
отклонения
ограничивается
рядом
отрицательных
факто
ров.
Во-первых,
использование
операции
дифференцирования
сопряжено
с
усиле
нием
помех
измерения
и
«зашумлением»
канала
управления.
Во-вторых,
компен
сация
возмущающего
влияния
внешних
воздействий
f
и
у*
требует
определенных
временных
затрат.
В-третьих,
для
задач
управления,
в
которых
начальные
зна
чения
отклонения
€
велики,
управляющие
воздействия
принимают
недопустимо
большие
значения.
Комбинированные
регуляторы.
Более
эффективный
метод
повышения
точности
САУ
предлагают
линейные
регуляторы
комбинированного
типа,
содержащие
кроме
7.3.
Реryляторы
и
системы
управления
:состоянием
209
8
б
у*
О
О
t t
K
D
=
0.2
2.0
f
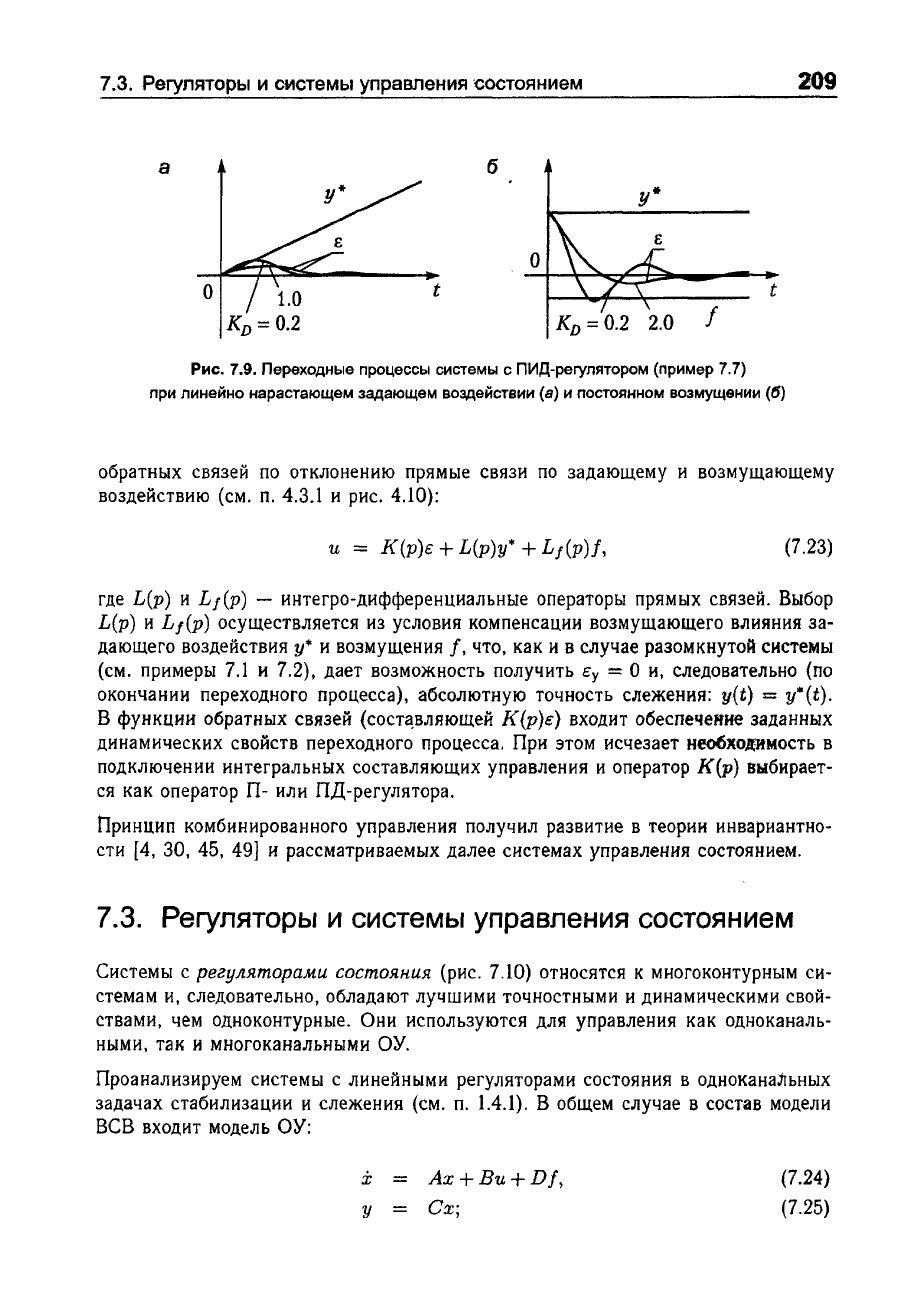
Рис.
7.9.
Переходные
процессы
системы
сПИД-регулятором
(пример
7.7)
при
линейно
нарастающем
задающем
воздействии
(а)
и
постоянном
возмущении
(6)
обратных
связей
по
отклонению
прямые
связи
по
задающему
и
возмущающему
воздействию
(см.
п.
4.3.1
и
рис.
4.l0):
и
=
K(p)€
+ L(P)y* +
Lf(p)J,
(7.23)
где
L(p)
и
Lf(P)
-
интегро-дифференциальные
операторы
прямых
связей.
Выбор
L(p)
и
Lf(p)
осуществляется
из
условия
компенсации
возмущающего
влияния
за
дающего
воздействия
у*
и
возмущения
j.
что,
как
и
в
случае
разомкнутой
системы
(см.
при
меры
7.1
и
7.2),
дает
возможность
получить
€y
=
О
и,
следовательно
(по
окончании
переходного
процесса),
абсолютную
точность
слежения:
y(t) = y*(t).
В
функции
обратных
связей
(сост~вляющей
K(p)€)
входит
обеслечеRие
заданных
динамических
свойств
переходного
процесса.
При
этом
исчезает
необхоД!ИМОСТЬ
в
подключении
интегральных
составляющих
управления
и
оператор
К(р)
выбирает
ся
как
оператор
п-
или
ПД-регулятора.
tlринцип
комбинированного
управления
получил
развитие
в
теории
инвариантно
сти
[4,
30,
45,
49]
и
рассматриваемых
далее
системах
управления
состоянием.
7.3.
Регуляторы
и
системы
управления
состоянием
Системы
с
регуляторамu
состоянuя
(рис.
7.10)
относятся
к
многоконтурным
си
стемам
и,
следовательно,
обладают
лучшими
точностными
и
динамическими
свой
ствами,
чем
одноконтурные.
Они
используются
для
управления
как
одноканаль
ными,
так
и
многоканальными
ОУ.
Проанализируем
системы
с
линейными
регуляторами
состояния
в
одноканальных
задачах
стабилизации
и
слежения
(см.
п.
1.4.1).
В
общем
случае
в
состав
модели
ВСВ
входит
модель
ОУ:
х
=
Ax+Bu+DJ,
у
=
Сх;
(7.24)
(7.25)
