Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.


230
Глава
7.
Методы
управления
и
синтез
еДУ
и
вырабатывает
текущие
значения
оценки
y(t)
выходной
переменной
y(t)
и
оценки
x(t)
вектора
состояния
x(t).
Поведение
модели
(7.115)-(7.116)
корректируется
за
счет
обратных
связей
по
выходной
ошибке
(невязке)
у
=
у-у
(7.117)
с
помощью
специального
векторного
входного
воздействия
наблюдателя
ин
=
{UHi}'
Введем
в
рассмотрение
вектор
ошибок
наблюдения
(вектор
невязок)
х
=
х-х,
(7.118)
характеризующий
отклонение
состояния
МОУ
ОТ
состояния
объекта
управления
(7.113).
Модель
ошибок
наблюдения
получается
дифференцированием
по
времени
выражения
(7.118)
и
после
подстановки
уравнений
(7.113)
и
(7.115),
а
также
с
учетом
(7.114)
и
(7.116)
принимает
вид
(рис.
7.25)
х
у
Ах
-
ин,
сх.
(7.119)
(7.120)
Модель
показывает,
что
при
ин
=
О
устойчивость
и
динамические
свойства
процес
са
оценивания
зависят
от
матрицы
А,
т.
е.
свойств
разомкнутой
системы
(самого
объекта
управления).
Задача
синтеза
наблюдателя
сводится
к
выбору
входного
воздействия
ин.
которое
обеспечивало
бы
устойчивость
модели
(7.119)
и,
следова
тельно.
устранение
с
течением
времени
отклонений
х
и
у.
Так
как
это
воздействие
не
должно
зависеть
от
вектора
ошибок
х
(значения
вектора
состояния
ОУ
х
В
рассматриваемом
случае
полагаются
неизвестными),
то
вектор
ин
формируется
на
основании доступной
информации
о
невязке
(7.117),
т.
е.
в
виде
обратных
связей
(7.121)
где
К
Н
-.--
матрица-стоЛбец
коэффициентов:
1..----1
К
Н
1+------'
Рис.
7.25.
Модель
ошибок
наблюдения

7:4.
Синтез
наблюдателей
состояния
или
n
скалярных
выражений
k
Hn
k
иn
-
1
k
H2
k
H1
UHi
=
khn-i+1У,
i =
1,
n.
231
Подставив
(7.121)
в
уравнение
(7.119),
получим
следующую
модель
ошибок:
5;
=
Ах
-
Ку
=
(А
-
КнС)х
=
Анх,
(7.122)
где
Ан
=
А
-
КнС
-
матрица
наблюдателя
(замкнутой
системы
оценивания),
определяющая
его
динамические
свойства.
Соответствующий
характеристический
полином
наблюдателя
представлен
выражением
(7.123)
Устойчивость
положения
равновесия
х
=
о
модели
(7.122)
и
заданные
динами
ческие
показатели
качества
наблюдателя
достигаются
за
счет
назначения
соот
ветствующих
корней
PHi
=
Лi
{Ан}
характеристического
уравнения
ан
(Р)
=
О,
что,
в
свою
очередь,
обеспечивается
соответствующим
выбором
коэффициентов
k
Hi
мат
рицы
обратных
связей
К
н
•
Метод
выбора
указанных
коэффициентов
основывается
на
следующем
положении.
Свойство
7.2.
Если
система
(7.113)-(7.114)
полностью
наблюдаема,
то
существует
единственная
матрица
обратной
связи
К
н
,
обеспечивающая
получение
заданных
значений
корней
характеристического
полинома
наблюдателя
PHi
=
Лi{А
н
}.
в
условиях
свойства
7.2
алгоритм
(7.121)
обеспечивает
с
течением
времени
(т. е.
асимnтотически
при
t
-----+
00)
выполнение
равенства
х
=
о
и,
следовательно,
х
=
х.
в
связи
с
этим
рассмотренная
схема
оценивания
переменных
состояния
называется
асимптотическим
наблюдателем.
Методика
выбора
коэффициентов
матрицы
К
Н
подобна
синтезу
пропорциональ
ного
регулятора
состояния
(7.31).
Однако
если
при
проектировании
регулятора
предпочтительно
воспользоваться
каноническим
управляемым
или
подобным
ему
описанием
объекта
управления
(см.
замечание
7.1),
то
при
построении
наблюда
теля
наиболее
удобными
оказываются
модели
ВСВ
в
канонической
наблюдаемой
или
близкой
к
ней
форме
(см.
3.4.2).
Пример
7.13.
Для
объекта
второго
порядка
(пример
7.8)
(7.124)

232
Глава
7.
Методы
управления
и
синтез
еДУ
введем
переменные
состояния
как
Тогда
модель
вев
примет
вид
(рис.
7.26)
Хl
=
-а2Хl
+
Ьи,
Х2
У
Х2
или
(7.113),
(7.114),
где
х
=
!:~
!'
А
=
!
о
-а
2
!,
В
1
-аl
1
о
1
1·
Рис.
7.26.
Каноническая
(наблюдаемая)
модель
системы
второго
порядка
Наблюдатель
состояния
рассматриваемого
ОУ
имеет
вид
(рис.
7.27)
Х1
=
-а2
Х
1
+
ин1,
Х2
=
-а1
Х
2
+
Хl
-
и
н
2,
У
=
Х2
или
(7.115)-(7.116),
где
Модель ошибок
наблюдения
(7.119)-(7.120)
принимает
вид
Выберем
входные сигналы
UHi
как
или
(7.125)
(7.126)
(7.127)
(7.128)
(7.129)
(7.130)
(7.131)
(7.132)
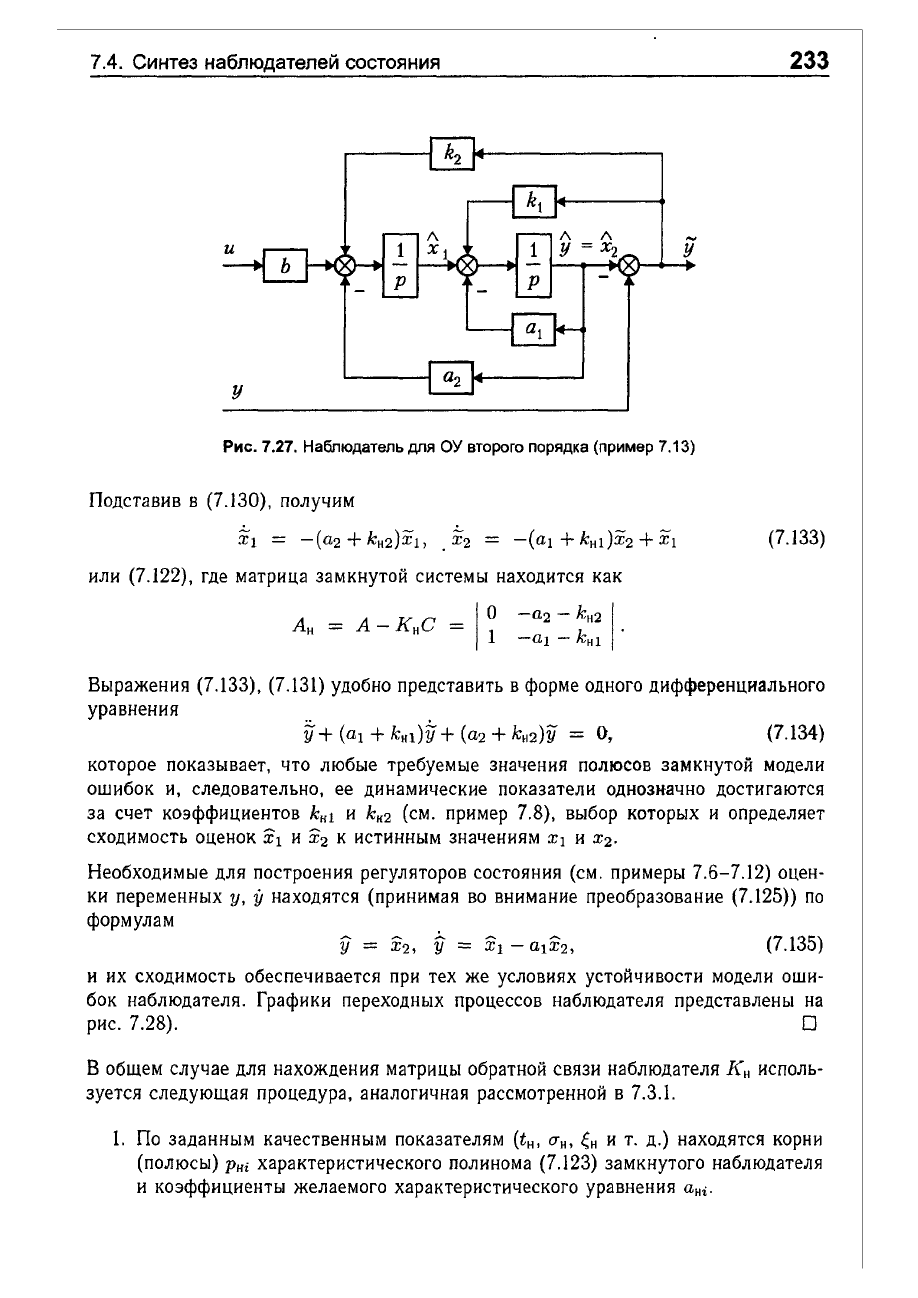
7.4.
Синтез
наблюдателей
состояния
2ЗЗ
у
Рис.
7.27.
Наблюдатель
ДЛЯ
ОУ
второго
порядка (пример
7.13)
Подставив
в
(7.130),
получим
:t'1
=
-(а2
+
k
и2
)Хl,
Х2
=
-(аl
+
k
и1
)Х2
+
Х1
(7.133)
или
(7.122),
где
матрица
замкнутой
системы
находится
как
А
и
=
А
_
КиС
= I
о
-а2
-
kИ21.
1
-аl
-
k
И1
Выражения
(7.133),
(7.131)
удобно
представить
в
форме
одного
дифференциального
уравнения
(7.134)
которое
показывает,
что
любые
требуемые
значения
полюсов
замкнутой
модели
ошибок
и,
следовательно,
ее
динамические
показатели
однозначно
достигаются
за
счет
коэффициентов
k
H1
и
k
H2
(см.
при
мер
7.8),
выбор
которых
и
определяет
сходимость
оценок
Хl
и
Х2
К
истинным
значениям
Х1 и
Х2.
Необходимые
для
построения
регуляторов
состояния
(см.
примеры
7.6-7.12)
оцен
ки
переменных
у,
iJ
находятся
(принимая
во
внимание
преобразование
(7.125»
по
формулам
(7.135)
и
их
сходимость
обеспечивается
при
тех
же
условиях
устойчивости
модели
оши
бок
наблюдателя.
Графики
переходных
процессов
наблюдателя
представлены
на
рис.
7.28).
О
в
общем
случае
для
нахождения
матрицы
обратной
связи
наблюдателя
К
И
исполь
зуется
следующая
процедура,
аналогичная
рассмотренной
в
7.3.1.
1.
По
заданным
качественным
показателям
(t
и
,
аи,
~и
и
т.
д.)
находятся
корни
(полюсы)
PHi
характеристического
полинома
(7.123)
замкнутого
наблюдателя
и
коэффициенты
желаемого
характеристического
уравнения
аиi.
234
Глава
7.
Методы
управления
и
синтез
еДУ
а
б
о
t
о
t
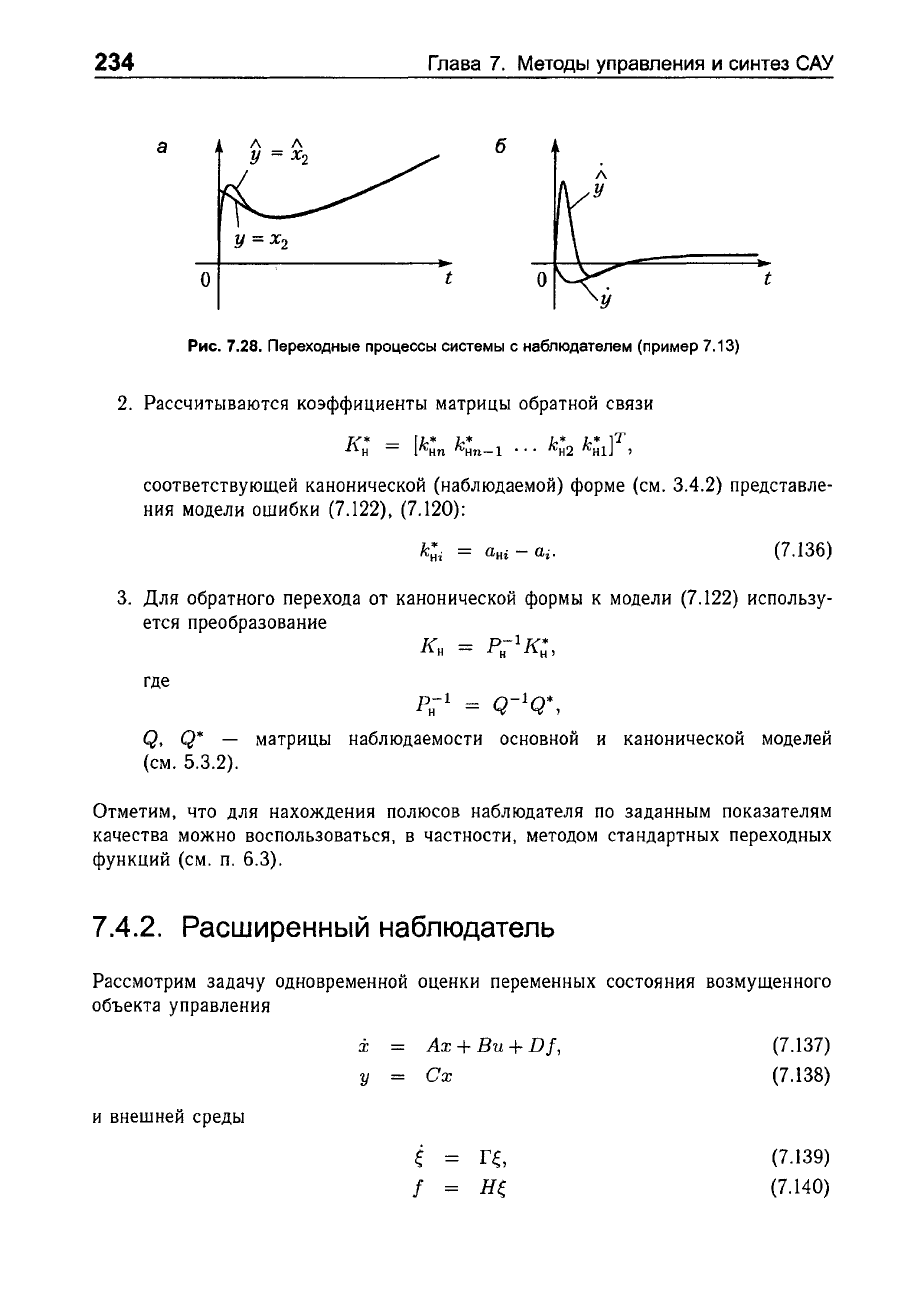
Рис.
7.28.
Переходные
процессы
системы
с
наблюдателем
(пример
7.13)
2.
Рассчитываются
коэффициенты
матрицы
обратной
связи
7.'*
[k* k* k*
k*]T
.н'Н
=
Нn
Hn-l
•..
н2
Hl
,
соответствующей
канонической
(наблюдаемой)
форме
(см.
3.4.2)
представле
ния
модели
ошибки
(7.122),
(7.120):
(7.136)
3.
Для
обратного
перехода
от
канонической
формы
к
модели
(7.122)
использу
ется
преобразование
где
PH-1
=
Q-IQ*,
Q,
Q*
матрицы
наблюдаемости
основной
и
канонической
моделей
(см.
5.3.2).
Отметим,
что
для
нахождения
полюсов
наблюдателя
по
заданным
показателям
качества
можно
воспользоваться,
в
частности,
методом
стандартных
переходных
функций
(см.
п.
6.3).
7.4.2.
Расширенный
наблюдатель
Рассмотрим
задачу
одновременной оценки
переменных
состояния
возмущенного
объекта
управления
у
и
внешней
среды
~
J
Ax+Bu+DJ,
Сх
Г~,
H~
(7.137)
(7.138)
(7.139)
(7.140)
7.4.
Синтез
наблюдателей
состояния
235
(см.
рис.
7.10
и
7.29)
по
доступным
измерениями
выходной
переменной
ОУ
y(t).
Сформируем
расширенную
модель
объекта,
включающую
описание
внешней
сре
ДЫ,
т.
е.
модель
вида
(7.141)
(7.142)
I
х
I u u
где
Х
р
=
~
-
nр-мерныи
вектор
состояния
расширеннои
модели,
Пр
= n +
nj,
_O\jA
DHI
Ар
-
О
Г
'
[С
О].
Рис.
7.29.
Расширенная
модель
объекта
управления
Отметим,
что
матрица
наблюдаемости
расширенной
модели
имеет
вид:
Расширенная
схема
наблюдения
включает
в
свой
состав
модель
расширенного
ОУ
Х
р
=
АрХ
р
+
ВрИ
+
Ир,
У
СрХ
р
и
обратные
связи
по
невязке
(7.117):
Ир
=
I{pY,
где
I{p
-
матрица-столбец
коэффициентов:
(7.143)
(7.144)
(7.145)

236
Глава
7.
Методы
управления
и
синтез
еДУ
Матрица
К
р
рассчитывается
в
соответствии
с
методикой,
рассмотренной
в
7.4.1,
с
учетом
необходимых
замен
А
на
Ар,
е
на
ер,
в
на
В
р
и
Q
на
Qp.
Прuмер
7.14.
Рассмотрим
возмущенный
объект
(7.44),
для
которого
модель
вев
принимает
вид
Хl
=
Х2,
Х2
У
=
Хl,
а
модель
внешней
среды
-
~1
f
О,
~1
(О)
=
60,
6·
(7.146)
(7.147)
(7.148)
(7.149)
Расширенная
модель
имеет
порядок
3
и
записывается
в
виде
(7.141)-(7.142),
где
Хl
О
1
О
О
Х
р
=
Х2
Ар
-а2
-аl
d
В
р
Ь
6
О
О
О
О
ер
=
I 1
О
О
1.
Для
оценки
переменных
расширенной
модели
по
измеряемой
выходной
переменной
y(t)
формируется
расширенная
(порядка
Пр
=
3)
модель
наблюдателя
Х2
+
ирl,
-а2
Х
l
-
аl
Х
2
+
Ьи
t"dj
+
ир2,
(7.150)
с
выходом
(7.151)
и
обратными
связями
по
невязке
у
=
у
-
у:
(7.152)
Последнее
выражение
можно
записать
в
компактной
форме
(7.145),
где
матрица
столбец
коэффициентов
обратной
связи
k
рз
К
р
= k
p2
k
p1
рассчитывается
по методике,
приведенной
в
7.4.1.
Переходные
процессы
системы
с
расширенным
наблюдателем
приведены
на
рис.
7.30,
а.
О
7.4.
Синтез
наблюдателей
состояния
237
а
б
о
t
о
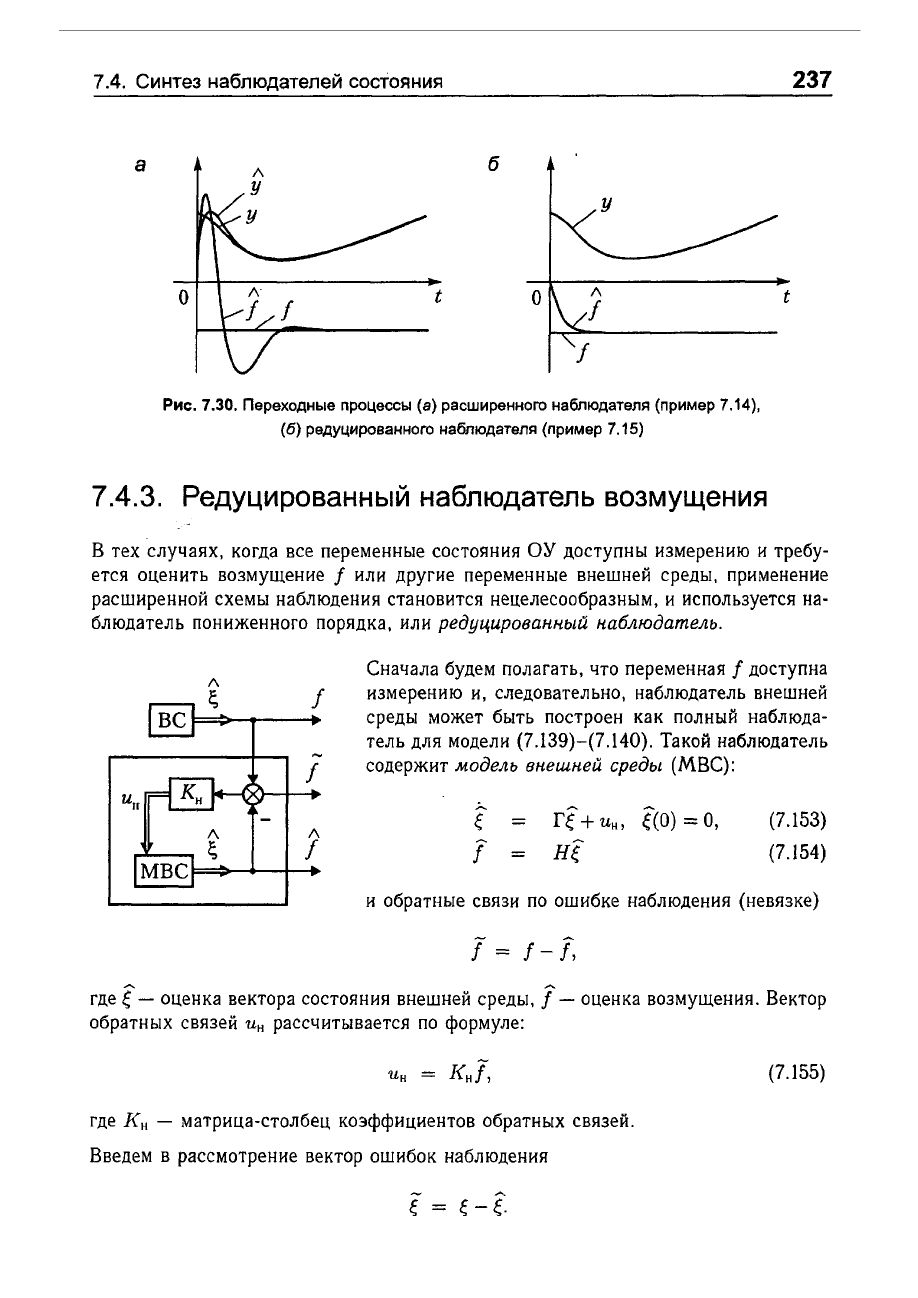
Рис.
7.30.
Переходные
процессы
(а)
расширенноro
наблюдателя
(пример
7.14),
(б)
редуцированного
наблюдателя
(пример
7.15)
t
7.4.3.
Редуцированный
наблюдатель
возмущения
В
тех
случаях,
когда
все
переменные
состояния
ОУ
доступны
измерению
и
требу
ется
оценить
возмущение
1
или
другие
переменные
внешней
среды,
применение
расширенной
схемы
наблюдения
становится
нецелесообразным,
и
используется
на
блюдатель
пониженного
порядка,
или
редуцированный
наблюдатель.
f
BCI==~"""---+
-
f
л
f
Сначала
будем
полагать,
что
переменная
1
доступна
измерению
и,
следовательно,
наблюдатель
внешней
среды
может
быть
построен
как
полный
наблюда
тель
для
модели
(7.139)-(7.140).
Такой
наблюдатель
содержит
модель
внешней
среды
(мве):
=
=
г[
+
ин,
[(О)
=
О,
Н[
(7.153)
(7.154)
и
обратные
связи
по
ошибке
наблюдения
(невязке)
1 =
1-1,
где
[ -
оценка
вектора
состояния
внешней
среды,
i -
оценка
возмущения.
Вектор
обратных
связей
ин
рассчитывается
по
формуле:
ин
=
!(Н!'
где
К
Н
-
матрица-столбец
коэффициентов
обратных
связей.
Введем
в
рассмотрение
вектор
ошибок
наблюдения
[=
~-[
(7.155)

238
Глава
7.
Методы
управлени~
и
синтез
еДУ
Модель
ошибок
наблюдения
получается
вычитанием
(7.153)
из
(7.139)
и
(7.154)
из
(7.140).
После
подстановки
(7.155)
модель
принимает
вид:
~
f
(7.156)
(7.157)
где
Г
и
=
Г
-
К
н
Н.
Выбор
матри
цы
обратной
связи
К
н
производится
в
соответствии
с
методикой,
изложенной
в
7.4.1.
Отметим
нереализуемость
построенного
наблюдателя
ввиду
использования
неиз
меряемого
возмущения
f.
Для
нахождения
реализуемой
схемы
наблюдения
модель
(7.153)-(7.155)
преобразуется
таким
образом,
чтобы
на
ее
вход
вместо
функции
f
поступали
измеряемые переменные
СОСТQ~ftИя.
С
этой
целью
формируется
вспомо
гательная
выходная
переменная
у'
=
С'х,
(7.158)
представляющая
собой
линейную
комбинацию
измеряемых
переменных
состояния
ОУ
xi,
причем
матрица-строка
С'
выбирается
из
условия
С'
D =
1.
Вектор
состояния
редуцированного
наблюдателя
определяется
выражением
z =
[-
I<иу',
(7.159)
а
уравнение
редуцированного
наблюдателя
(РН,
рис.
3.31)
находится
дифферен
цированием
выражения
(7.159)
по
времени
и
после
подстановки
(7.156),
(7.137),
(7.158)
принимает
вид:
i =
Г
иz
+
(Г
нКнС'
-
КнС'
А)х
-
I<иС'
Вu,
z(O)
=
О.
(7.160)
Для
получения
~скомой
оценки
[
вектора
состояния
внешней
среды
используется
выражение,
полученное
из
уравнений
(7.158)
и
(7.159):
[ =
z+KHC'x,
(7.161)
а
для
получения
оценки
1
возмущающего
воздействия
-
выражение
(7.154).
л
л
~
f
Рис.
7.31.
Редуцированный
наблюдатель
внешней
среды
Пример
7.15.
Рассмотрим
задачу
синтеза
наблюдателя
возмущения
объекта
(7.146)
с
моделью
внешней
среды
(7.148)
(см.
пример
7.14).
На
начальном
этапе,
полагая

7.5.
Регуляторы
выхода
и
принцип
разделения
возмущение
f
измеримым,
сформируем
наблюдатель
внешней
среды
где
сигнал
обратной
связи
и
Н
1
рассчитывается
по
формуле:
239
(7.162)
(7.163)
(7.164)
1 = f -
1.
k
и1
>
О.
Отметим,
что
ошибка
наблюдения
[1
= 1
описывается
ура
вне-
нием
- -
f =
-k
и1
f·
Для
нахождения
реализуемой
схемы
наблюдения
сформируем
вспомогательную
выходную
переменную
у'
=
Х2
(7.165)
и
промежуточную
переменную
zl
=
1-
kи1Х2.
В
соответствии
с
выражениями
(7.160)-(7.161)
редуцированный
наблюдатель
(модель
l-го
порядка)
принимает
вид
Zl
=
-k
н1
Z
1
-
k~lX2
-
k
и1
Ьu,
f = z +
k
и1
Х
2.
(7.166)
(7.167)
Переходные
процессы
системы
с
редуцированным
наблюдателем
возмущения
при
ведены
на
рис.
7.30,
б.
О
7.5.
Регуляторы
выхода
и
принцип
разделения
Оценки
переменных
состояния,
полученные
с
помощью
рассмотренных
в
п.
7.4
наблюдателей
состояния
используются
в
соответствующих
алгоритмах управления
САУ.
При
этом
полученные
в
п.
7.3
алгоритмы
модифицируются
-
переменные
состояния
объекта
управления
и
внешней
среды
замещаются
их
оценками.
Так,
наиболее
общий
алгоритм
управления,
обеспечивающий
решение
задачи
слежения
для
возмущенной
системы
(см.
7.3.2
и
7.3.3)
принимает
вид
(7.168)
где
е
=
М*;с*
-
х,
(7.169)
-
оценка
ошибки
слежения
e(t),
а
х
и
f -
оценки
вектора
состояния
x(t)
объекта
управления
и
вектора
состояния
~(t)
внешней
среды
соответственно.
Последние
могут
быть
получены
с
помощью
расширенного
наблюдателя
типа
(7.143)-(7.145).
