Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.


260
Глава
8.
Дискретные
системы
и,
следовательно,
(1
-
А)х*
=
О.
(8.94)
При
условии
det(I
-
А)
:f=
О
получаем,
что
единственным
положением
равновесия
системы
(8.82)
является
начало
координат
пространства
состояний
IRn,
т.
е.
х*
=
О,
а
при
det(1
-А)
=
О
существуют
нетривиальные
множества
равновесных
состояний
(прямые,
плоскости
-
подпространства),
удовлетворяющие
уравнению
(8.94).
Как
будет
показано
в
8.2.2,
равновесное
состояние
х
=
О
аси~птотически
устой
чиво
и,
следовательно,
x(k) --+
О
при
k --+
00,
если
в~полняется
(8.95)
Рассмотрим
систему
с
нулевыми
значениями
корней
характеристического
полино
ма
(или
собственных
чисел
матрицы
А):
Zi
=
Лi{А}
=
О,
i = 1,n.
В
этом
случае
матрица
А
является
н,uльnоmен,mн,ой
и,
следовательно,
найдется
целое
число
m
Е
[О,
n]
такое,
что
О.
(8.96)
Для
такой
системы
всегда
выполняется
(8.97)
т.
е.
имеет
место
следующее
положение.
Свойство
8.2.
Переходный
процесс
дискретной
системы
n-го
порядка
с
нулевы
ми
значениями
всех
полюсов
zi
сходится
из
произвольного
начального
состояния
х(О)
=
хо
к
положению
равновесия
х
=
О не
более
чем
за
n
шагов.
Перечисленные
асимптотические
свойства
автономных
моделей
состояния
спра
ведливы
также
для
выходной
переменной
y(k) = Cx(k),
и
для
свободных
состав
ляющих
переходных
процессов
xcB(k)
и
YCB(k)
возмущенных
дискретных
систем.
Рассмотрим
поведение
модели
ВСВ
(8.75)-(8.76)
при
постоянном
входном
воздей
ствии
u(k)
;::;
const
и
проанализируем
установившиеся
составляющие
переходного
процесса
xy(k)
и
Yy(k).
Замечая,
что
в
рассматриваемом
режиме
~истема
(8.75)
имеет
решение
Xy(k);::; const,
запишем
xy(k +
1)
= xy(k).
Тогда
само
уравнение
(8.75)
принимает
вид
Х
у
=
Аху
+
Бu.
(8.98)
При
условии,
что
det(I
-
А)
:f=
О,
алгебраическое
уравнение
(8.98)
единственным
образом
разрешимо
относительно
Х
у
:
Х
у
=
-(1
-
A)-l
Вu.
(8.99)

8.1.
Дискретные
модели
динамических
процессов
261
Подставляя
найденное
решение
в
уравнение
выхода
(8.76),
находим
статическую
характеристику
рассматриваемой
дискретной
системы:
Уу
=
-C(I
-
A)-l
Вu,
(8.l00)
где,
в
силу
выражения
(8.79),
C(I
-
A)-l
В
= W(1).
(8.101)
Отметим
что
для
асимптотически
устойчивой
системы,
удовлетворяющей
усло
вию
(8.95),
всегда
выполняется
det(I
-
А)
=1-
о,
т.
е.
установившиеся
решения
единственны.
Более
того,
переходные
процессы
x(k)
и
y(k)
с
течением
времени
k
всегда
сходятся
к
найденным
выше
установившимся
значениям
Х
у
И
уу.
8.1.4.
Элементарные
звенья
дискретных
систем
в
качестве
элементарных
звеньев
выделим
простейшие
блоки
дискретной
систе
мы,
описывающиеся
разностными
уравнения
1-2-го
порядков
и
удовлетворяющие
условию
Элементарные
звенья
l-го
порядка.
Звенья
задаются
уравнениями
y(k + 1)-+ ay(k) = bu(k),
обладают
передаточной
функцией
W(z) =
ь
z+a
и
полюсом
(корнем
характеристического
уравнения)
Zl
=
-а.
Решение
уравнения
(8.103)
находится
как
k-l
y(k) =
YCB(k)
+
YB(k)
=
(-a)k
xo
+
Ь
I)
_a)k-i-l
u
(i).
i=O
(8.102)
(8.103)
(8.104)
При
Ь
= 1
и
а
=
О
получаем
звено
чистого
запаздывания
(элемент
задержки)
с
передаточной
функцией
y(k +
1)
= u(k),
1
W(z) =
z
(8.105)

212
Глава
8.
Дискретные
системы
При
а
=
-1
получаем
суммирующее
звено
(дискретный
интегратор)
с
передаточной
функцией
y(k +
1)
= y(k) + bu(k)
W(z)
ь
z-l
Уравнение
(8.106)
имеет
решение
k-l
y(k) =
у(О)
+
Ь
L u(i),
i=O
(8.106)
(8.107)
которое
показывает,
что
звено
является
дискретным
аналогом
интегрирующего
звена
(см.
п.
2.3).
Imz1
-1
О
1
Re
z1
Проанализируем
свободные
составляющие
пере
ходных
процессов
звеньев
первого
порядка
для
различных
значений
параметра
а
и,
следова
тельно,
различных
значений
полюсов
Zl
=
-а.
Для
этого
рассмотрим
автономную
систему
y(k + 1) + ay(k) =
О
(8.108)
с
начальным
значением
УО
=
у(О).
Решением
уравнения
(8.108)
является
функция
различные
реализации
которой
при
УО
= 1
приведены
на
рис.
8.11.
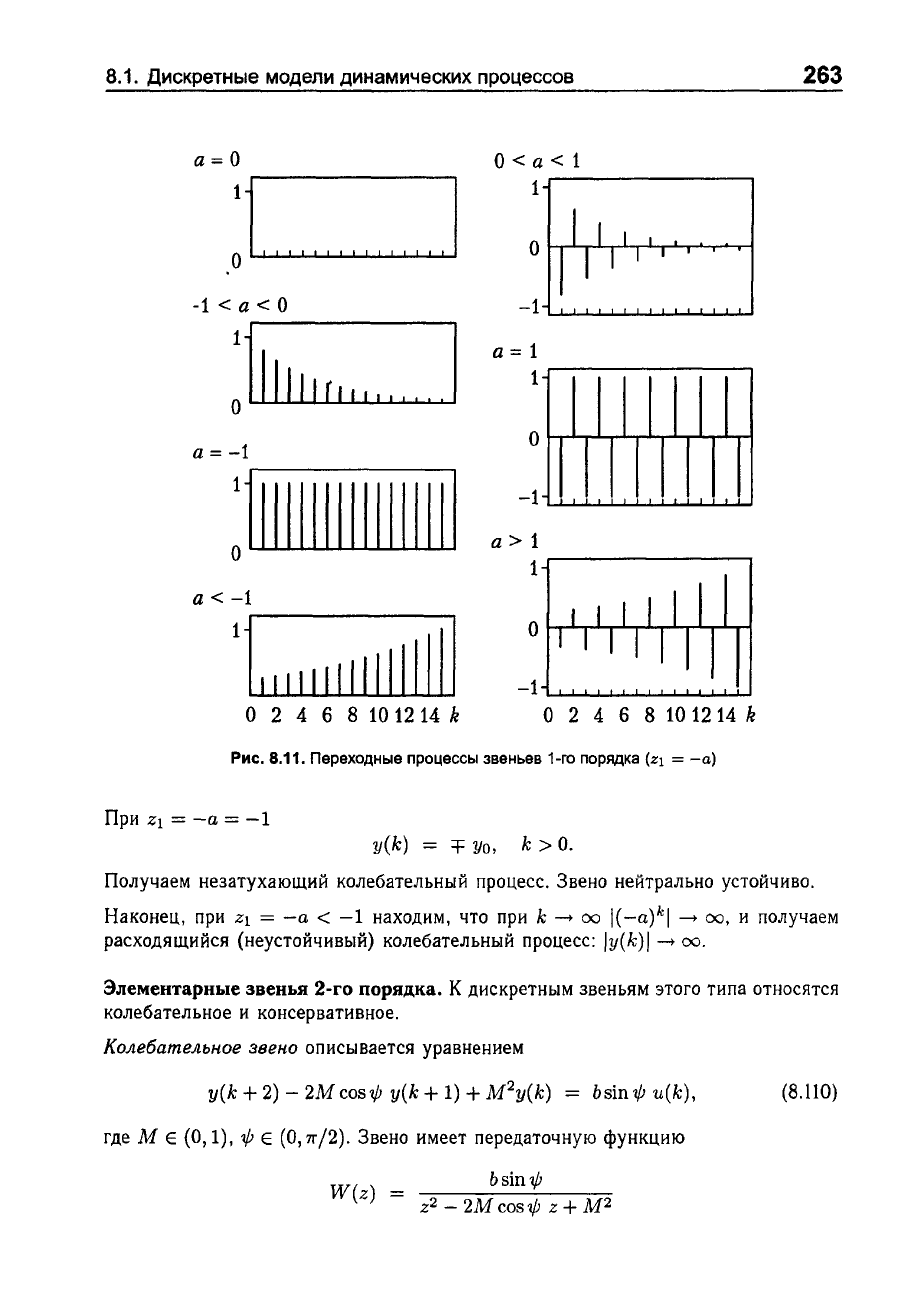
При
Zl
=
а
=
О
получаем
y(k) =
О,
k >
О,
(8.109)
т.
е.
из
произвольного
начального
положения
УО
процесс
сходится
к
нулевому
(равновесному
состоянию)
за
один
шаг.
При
Zl
=
-а
Е
(0,1)
имеем:
(_a)k
~
О
при
k
~
00,
и
получаем
апериодический
затухающий
процесс:
y(k)
~
О.
Звено
асимптотически
устойчиво.
При
Zl
=
-а
= 1
(суммирующее
звено)
находим
у(
k)
=
уо,
k >
О.
Звено
нейтрально
устойчиво.
Наконец,
при
Zl
=
-а
> 1
находиМ,
что
при
k
~
00
(_a)k
~
00,
и
получаем
апериодический
расходящийся
процесс:
\y(k)\
~
00.
Звено
неустоЙчиво.
При
отрицательных
значениях
Zl
=
-а
переходные
процессы
приобретают
коле
бательный
характер.
При
Zl
=
-а
Е
(-1,
О)
получаем
(-a)k
~
О
при
k
~
00,
и
затухающий
колебательный
процесс:
y(k)
~
О.
Звено
асимптотически
устойчиво.
8.1.
Дискретные
модели
динамических
процессов
263
а;::
О
0<а<1
~1,
I I I I I I I I I I I I I
II
1,------------,
-1
<
а
<
О
~111111f111"
1"
о
1
а
= 1
1....----------.
а;::
-1
~
11111111111111111
а> 1
1....---------,
а
<-1
111111111111111111
-1~~~~~~~~
О
2 4 6 8
10 12
14
k
О
2 4 6 8
10
12 14
k
Рис.
8.11.
Переходные
процессы
звеньев
1-го
порядка
(Zl
=
-а)
При
Zl
=
-а
=
-1
у(
k)
=
=F
Уа,
k >
О.
Получаем
незатухающий
колебательный
процесс.
Звено
нейтрально
устойчиво.
Наконец,
при
Zl
=
-а
<
-1
находим,
что
при
k ~
00
'(
_a)kl ~
00,
и
получаем
расходящийся
(неустойчивый)
колебательный
процесс:
ly(k)1
~
00.
Элементарные
звенья
2-го
порядка.
К
дискретным
звеньям
этого
типа
относятся
колебательное
и
консервативное.
Колебательное
звено
описывается
уравнением
y(k +
2)
-
2М
cos
Ф
y(k +
1)
+ M
2
y(k) = bsin
Ф
u(k),
(8.110)
где
М
Е
(0,1),
Ф
Е
(О,
1г
/2).
Звено имеет
передаточную
функцию
W(
)
Ьsiпф
Z =
z2
_
2М
cos
Ф
Z +
М2

264
Глава
8.
Дискретные
системы
и
комплексно-сопряженные
полюсы
Zl,2
=
Ме~jф
=
M(cos'lj;~jsin'lj;).
Звено
асимптотически
устойчиво
и
имеет
статическую
характеристику
bsin'lj;
у = .
1 -
2М
cos
'lj;
+
М2
Консервативное
звено
(дискретный
осциллятор)
описывается
уравнением
y(k + 2) - 2
cos'lj;
y(k + 1) + y(k) =
bsin
Ф
u(k),
(8.111)
где
'lj;
Е
(О,
1г
/2),
имеет
передаточную
функцию
bsin'lj;
W (z) =
z2
_ 2 cos
'lj;
z + 1
и
комплексно-сопряженные
полюсы
Zl,2
=
е~jф
= cos
'lj;
~
j
sin
'ф.
Звено
нейтрально
устойчиво
и
не
имеет
статической
характеристики.
Консервативное
звено
(8.111)
легко
приводится
в
форме
вев.
Определим
перемен
ные
состояния
из
выражений
и
запишем
Imz
xl(k+1)
X2(k
+
1)
y(k)
Хl
(k) = y(k),
sin'lj; x2(k) = y(k + 1) -
cos'lj;
y(k)
=
cos'lj;
Хl
(k) + sin'lj; x2(k)),
- sin'lj;
Хl
(k) +
cos'lj;
x2(k)) +
bsin
'lj;
u(k),
xl(k).
(8.112)
(8.113)
(8.114)
(8.115)
(8.116)
Проанализируем
свободные
составляющие
переходных
процессов
звеньев
второго
порядка
с
комплексными
полюсами
Zl,2
для
различных
значений
пара
метра
М.
ДЛЯ
этого
рассмотрим
автономную
систему
y(k +
2)
-
2М
cos'lj;y(k +
1)
+ M
2
y(k) =
О
(8.117)
с
начальными
значениями
у(О)
= 1
и
у(
-1)
=
=
м-l
cos'lj;.
Решения
уравнения
(8.117)
имеют
вид
y(k) =
(1vl)k
cos'lj;k.
(8.118)
8.2.
Основные
свойства
дискретных
систем
265
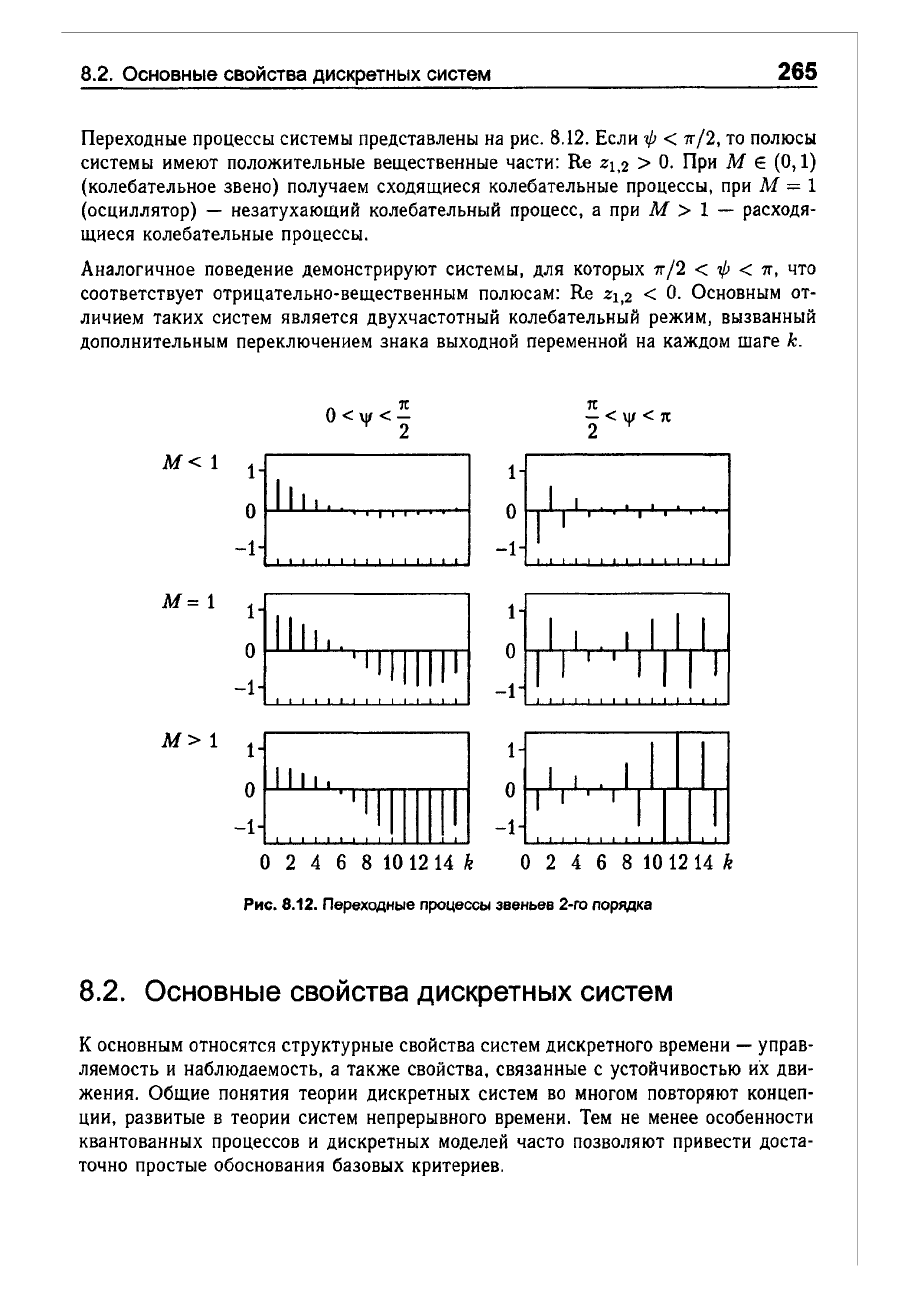
Переходные
процессы
системы
представлены
на
рис.
8.12.
Если
Ф
<
1г
/2,
то
полюсы
системы
имеют
положительные
вещественные
части:
Re
Zl,2
>
О.
При
М
Е
(0,1)
(колебательное
звено)
получаем
сходящиеся
колебательные
процессы,
при
М
= 1
(осциллятор)
-
незатухающий
колебательный
процесс,
а
при
М
> 1 -
расходя
щиеся
колебательные
процессы.
Аналогичное
поведение
демонстрируют
системы,
для
которых
1г
/2
<
Ф
<
1Г,
что
соответствует
отрицательно-вещественным
полюсам:
Re
Zl,2
<
О.
Основным
от
личием
таких
систем
является
двухчастотный
колебательный
режим,
вызванный
дополнительным
переключением
знака
выходной
переменной
на
каждом
шаге
k.
1t 1t
0<",<-
-<"'<1t
2 2
М<
1
1
1
О
О
-1
-1
М=
1
1 1
О
О
-1
-1
М>
1
1 1
О О
-1 -1
О
2 4 6 8
10
12
14
k
О
2 4 6 8
10
12 14
k
Рис.
8.12.
Переходные
процессы
звеньев
2-го
порядка
8.2.
Основные
свойства
дискретных
систем
к
основным
относятся
структурные
свойства
систем
дискретного
времени
-
управ
ляемость
и
наблюдаемость,
а
также
свойства,
связанные
с
устойчивостью
их
дви
жения.
Общие
понятия
теории
дискретных
систем
во
многом
повторяют
концеп
ции,
развитые
в
теории
систем
непрерывного
времени.
Тем
не
менее
особенности
квантованных
процессов
и
дискретных
моделей
часто
позволяют
привести
доста
точно
простые
обоснования
базовых
критериев.

266
Глава
8.
Дискретные
системы
8.2.1.
Управл~емость
и
на6людаемость
Будем
рассматривать
одноканальные
дискретные
системы
(объекты
управления)
x(k
+
1)
= Ax(k) + Bu(k),
y(k)
= Cx(k),
(8.119)
(8.120)
где
u(k) -
ска~ярное
управляющее
воздействие,
y(k) -
скалярная
выходная
пе
ременная,
k
2:
О,
х(О)
=
хо.
Проанализируем
проблемы
управляемости
и
наблюда
емости
дискретных
ОУ,
связанные
со
свойствами
тройки
матриц
(А,
В,
С).
u
о
12
n-1 k
Пробле.ма
управляемости
сводится
к
вопросу
о
су
ществовании
ограниченного
управляющего
воздей
ствия
и
= u(k), k
Е
[О,
k
f
],
переводящего
систе
му
(8.119)
из
произвольного
начального
состояния
х(О)
=
хо
в
произвольную
точку
пространства
состо
яний
x(k
f
)
=
х!
за
конечное
время.kf
(точное
опре
деление
управляемости
дискретной
системы
практи
чески
повторяет
определение
5.8).
Напомним,
что
свойство
управляемости
не
зависит
от
выходной
пе
ременной
у
и
поэтому
может
быть
определено
как
свойство
модели
(8.119)
или
пары
(А,
В).
Критерии
управляемости
дискретной
системы
иден
тичны
свойствам
5.6-5.8
(см.
5.3.1).
Основной
крите
рий
(свойство
5.6)
связывает
полную
управляемость
с
невырожденностью
матрицы
управляемости
и
=
[В/АВ/
...
/A
n
-
1
В]
и
для
одноканальной
системы
формулируется
в
виде:
det
и
i:-
О.
(8.121)
Доказательство
основного
критерия
управляемости
для
дискретной
системы
строится
на
базе
опре.liеления
управляемости
и
предусматривает
нахождение
в яв
ном
виде
импульсной
последовательности
u(k),
обеспечивающей
перевод
системы
(8.119)
в
произвольную
конечную
точку
x(k
f
) =
xf.
Используя
общую
формулу
(8.86),
найдем
значение
вектора
состояния
х
в
момент
k=n:
х(n)
=
Аnхо
+ A
n
-
1
Вu(О)
+ ... +
АВu(n
-
2)
+
Вu(n
- 1).
Выберем
kJ
=
11,
х(n)
=
Х!
и
перепишем
последнее
уравнение
в
виде
u(n -
1)
х!
=
Аnхо
+
[В/АВ/
...
/A
n
-
1
В]
u(n -
2)
u(О)
(8.122)
(8.123)

8
..
2
..
OCHoB!:tbte
,СSQй~тва
дискретных
систем
Это
алгебраическое
уравнение
разрешимо
относительно
вектора
(u(n -
1)~
u(n
~
-2),
...
,
u(О»
тогда
и
только
тогда,
когда
матрица
управляемости
И
обраП1м'а,
т.
е.
выполняется
условие
(8.121).
Находим
u(n
-
1)
u(n
-
2)
u(О)
, (8.124)
Таким
образом,
найдена
импульсную
последовательность,
которая
за
конечный
от
резок
времени
[О,
n]
приводит
вектор
состояния
x(k)
в
любую
заданную
точку
xf.
Необходимым
и
достаточным
условием
существования
такой
последователь~ости
является
условие
(8.121),
что
и
доказывает
основной
критерий.
Более
того,
на
осно
вании
вышеизложенного
можно
сформулировать
следующий
полезный
:результат.
Свойство
8.3.
Если
дискретная
система
порядка
n
полностью
управляема,
то
она
может
быть
переведена
из
произвоJihНОГО'
начального
состояния
хо
Е
IRn
в
произвольное
конечное
состояние
Х
=
Х
f
за
конечное
время
k = n.
Нетрудно
показать,
что
значение
k = n
соответствует
минимальному
времени
пере
ходного
процесса
линейной
дискретной
системы,
или
минимальному
чи'Слу
шагов
дJ1я
достижения
заданного конечного состояния
Х
f.
Это
коррелирует,
с,
известной
в
теории
оптимальных
систем
теоремой
об'n
интервалах
(см.
[27,
35,'
40]),
и
со
ответствующее
управление
дискретной
системы:
иногда
называется
оптимальным
по
быстродействию.
Более
того,
принимая
во
внимание
свойство
8.2
(см.
8.1.3)
можно
сделать
вывод
о
том,
что
для
получения
оптимального
быстродействия
за
мкнутая
система
должна
иметь
n нулевых
полюсов.
у
о
12
n-l
t
Проблема
наблюдаемости
одноканальной
дискрет
ной
системы
сводится
к
вопросу
об
единственности
решения
задачи
восстановления
вектора
состояния,
т.
е.
нахождения
вектора
;;(k)
в
момент
времени
k =
О
по
известным
измерениям
выходной
пер'емен
ной
у
= y(k)
при
k
Е
[О,
k
f
],
k
f
>
()
и
из'вестным
значениям
входной
переменной
u(k)
(см.
определение
5.9).
Напомним,
что
свойство
наблюдаемости
не
за
висит
от
входной
переменной
и
И
поэтому
может
быть
определено
как
свойство
автономной
модели
(8.82)-
(8.83)
или
парJз~
(А,
С).
Критерии
наблюдаемости
дискретной
системы
повто-
Х2
ряют
свойства
5.9-5.12
(см.
5.3.2).
Основной
крите
рий
(свойство
5.10)
связывает
полную
управляемость
с
невырожденностью
матрицы
наблюдаемости
268
Глава
8.
Дискретные
системы
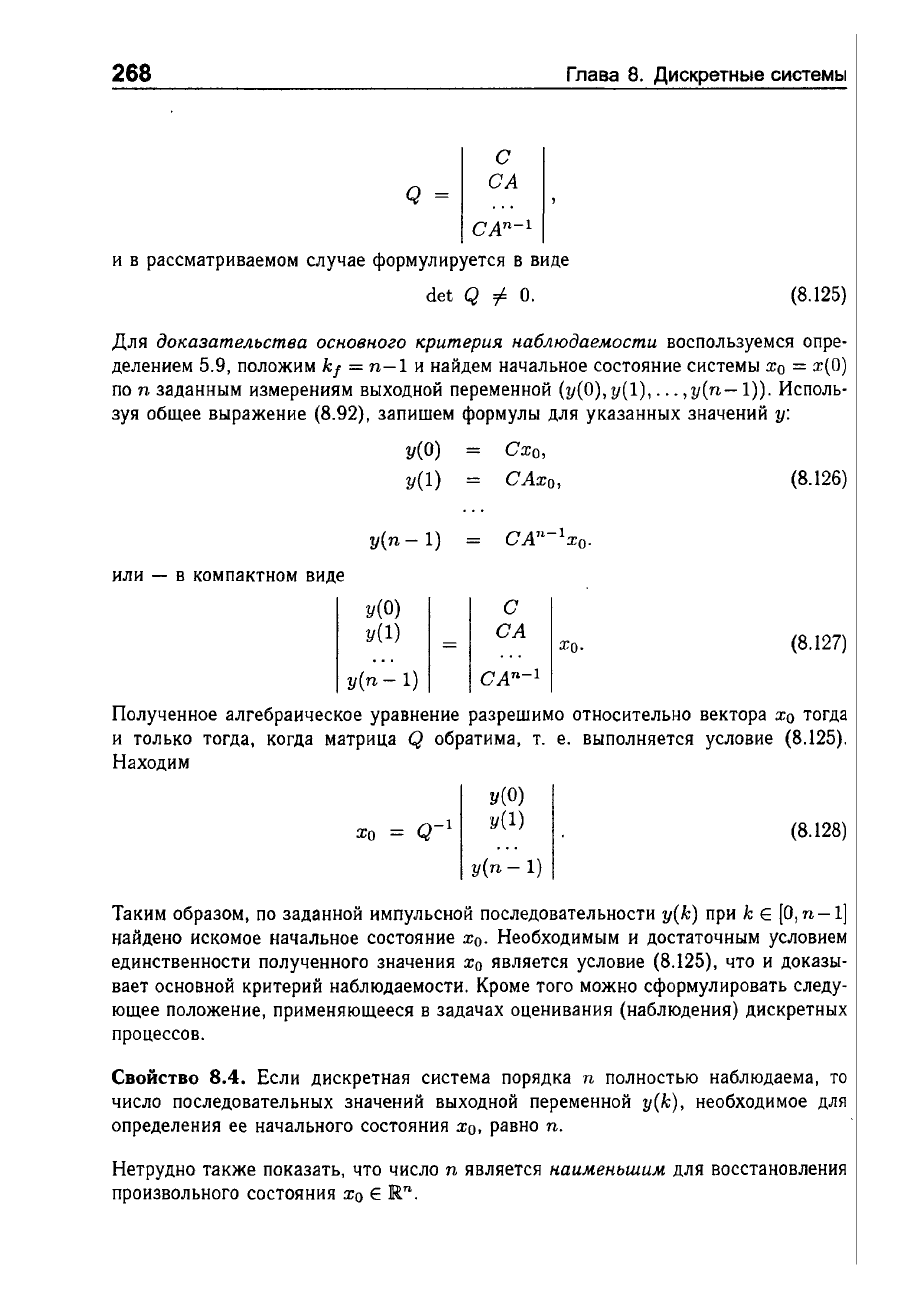
Q
С
СА
CAn-l
и
в
рассматриваемом
случае
формулируется
в
виде
det
Q
=1-
О.
(8.125)
Для
доказательства
основного
критерия
наблюдаемости
воспользуемся
опре
делением
5.9,
положим
k
f
=
n-1
и
найдем
начальное
состояние
системы
Ха
=
х(О)
по
n
заданным
измерениям
выходной
переменной
(у(О),
у(1),
...
,
у(n-1)).
Исполь
зуя
общее
выражение
(8.92),
запишем
формулы
для
указанных
значений
у:
у(О)
=
СХа,
у(1)
=
САХа,
(8.126)
у(n
-
1)
=
CAn-1Ха.
или
-
в
компактном
виде
у(О)
С
у(1)
СА
Ха·
(8.127)
у(n
-
1)
CAn-l
Полученное
алгебраическое
уравнение
разрешимо
относительно
вектора Ха
тогда
и
только
тогда,
когда
матрица
Q
обратима,
т.
е.
выполняется
условие
(8.125).
Находим
Ха
у(О)
у(1)
у(n
-
1)
(8.128)
Таким
образом,
по
заданной
импульсной
последовательности
y(k)
при
k
Е
[О,
n-l]
найдено
искомое
начальное
состояние
Ха.
Необходимым
и
достаточным
условием
единственности
полученного
значения
Ха
является
условие
(8.125),
что
и
доказы
вает
основной
критерий
наблюдаемости.
Кроме
того
можно
сформулировать
следу
ющее
положение,
применяющееся
в
задачах
оценивания
(наблюдения)
дискретных
процессов.
Свойство
8.4.
Если
дискретная
система
порядка
n
полностью
наблюдаема,
то
число
последовательных
значений
выходной
переменной
y(k),
необходимое
для
определения
ее
начального
состояния
Ха,
равно
n.
Нетрудно
также
показать,
что
число
n
является
наименьшим
для
восстановления
произвольного
состояния
Ха
Е
Rn.

8.2.
Основные
свойства
дискретных
систем
269
8.2.2.
УСТОЙЧИВОСТЬ
дискретных
систем
Как
и
для
систем
непрерывного
времени,
под
устойчивостью
дискретной
систе
мы
понимают
ее
способность
возвращаться
в
равновесное
состояние
(положение
равновесия)
после
окончания
действия
внешних
факторов.
Тем
самым
предпола
гается,
что
рассматривается
свободное
движение
управляемой
системы
YCB(k)
или
xcB(k),
либо
движение
автономной
системы
при
ненулевых
начальных
условиях
у(о),
У(
-1),
...
,
У(
-n
+
1)
или
х(о)
соответственно.
Автономная
система
описывается
уравнениями
или
a(z)y(k) =
О
x(k +
1)
= Ax(k),
y(k)
= Cx(k),
имеет
характеристический
полином
a(z) =
det(zI
-
А)
= zn +
alz
n
-
1
+ ... +
а
n
и
полюсы
Zi
=
Лi{А},
i =
1,
n.
(8.129)
(8.130)
(8.131)
(8.132)
Ее
равновесное
состояние
(см.
8.1.3)
для
модели
(8.129)
принимает
значение
у*
=
=
о,
а
для
модели
(8.130) -
х*
=
о.
Основные
понятия
устойчивости
линейных
дискретных
систем
практически
пол
ностью
идентичны
соответствующим
понятиям
непрерывных
систем
(см.
п.
5.1).
Здесь
ограничимся
рассмотрением
свойства
асимптотической
устойчивости,
кото
рое
в
рассматриваемом
случае
сводится
к
аттрактивности
положений
равновесия.
Устойчивость
по
выходу
(техническая
устойчивость)
определяется
характером
изменения
выходной
переменной
y(k),
т.
е.
свойствами
решений
системы
(8.129)
или
соответствующего
выхода
системы
(8.130)-(8.131):
система
(8.129)
называется
устойчивой,
если
выполняется
Нm
y(k) =
о.
k-oo
(8.133)
Устойчивость
по
состоянию
определяется
характером
изменения
вектора
состо
яний
x(k),
т.
е.
свойствами
решений
системы
(8.130):
система
(8.130)
называется
асимптотически
устойчивой,
если
выполняется
Нm
Ix(k)1
=
о.
k-oo
(8.134)
