Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.


250
';Глава
8.
ДИскретные
си'стемы
где
используются
операторы
a(z) zn +
alz
n
-
1
+ ... +
an-lz
+
а
n
,
b(z) =
bIZ
11
-
1
+ ... + bn-1p + zn.
(8.34)
(8.35)
Оператор
a(z)
называется
характеристическим
полиномом
системы
(8.31),
а
ком
плексные
числа
Zi,
i =
Т:N,
являющиеся
корнями
характеристического
уравнения
a(z) =
О,
(8.36)
называются
полюсами
системы.
Корни
алгебраического
уравнения
b(z) =
О,
(8.37)
т.
е.
комплексные
числа
z?,
i =
1,
т,
называются
нулями
системы
(8.31).
и~)
~
Из
уравнения
(8.33)
найдем
явную
связь
переменных
y(k)
и
u(k)
в
виде
операторного
уравнения:
где
оператор
y(k)
=
W(z)
u(k),
W(z)
= b(z)
a(z)
называется
передаточной
функцией
дискретной
системы
(8.31).
(8.38)
(8.39)
Описание
автономной
дискретной
системы
дается
однородным
уравнением
вида
y(k
+
n)
+
aly(k
+ n -
1)
+ ... +
any(k)
-
О
(8.40)
или,
в
операторной
форме,
-
уравнением
a(z)
y(k)
=
о.
(8.41)
Возмущающее
воздействие
f(k),
характеризующее
влияние
на
объект управления
внешней
среды
(см.
п.
1.2),
рассматривается
как
дополнительный
входной
сигнал.
Тогда
линейная
модель
дискретной
системы
принимает
вид
y(k
+ n) +
aly(k
+ n -
1)
+ ... +
an-ly(k
+
1)
+ any(k) =
= b1u(k + n
-1)
+ ... + bn-1u(k +
1)
+ bnu(k) +
+
d1f(k
+ n -
1)
+
'"
+
dn-1f(k
+
1)
+
dnf(k),
(8.42)

8.1.
Дискретные
модели
динамических
процессов
·251
где
d
i
-
коэффициенты,
определяющие
влияние
на
процессы
в
системе
возмуще
ния
f(k).
После соответствующих
преобразований
получаем
операторную
форму
модели
(8.42):
a(z) y(k)
=
b(z)
u(k) + d(z)
f(k).
(8.43)
где
используется оператор
d(z)
=
d1z
n
-
1
+ ... +
dn-1P
+
Zn,
И
форму
y(k)
W(z) u(k) + Wf(z)
f(k),
(8.44)
где
W (z) = d(z)
f a(z)
-
передаточная
функция
по
возмущающему
воздействию
j(k).
Решение
разностных
уравнений.
Сама
форма
представления
моделей
вход-выход
указывает
простой
путь
для получения
рекуррентного
решения,
т.
е.
процедуры
нахождения
текущих
значений
y(k)
по
известным
значениям
У
и
u
в
предшеству
ющие
моменты
дискретного
времени
k.
Подставляя
в
разностное
уравнение
(8.31)
k + n = 1
и
принимая
во
внимание
предисторию
управляющего
сигнала
(8.32),
найдем
у(1)
=
-аlУ(О)
-
а2у(-1)
-
...
-
аnу(-n+
1)
+
b1u(0).
(8.45)
При
k + n = 2
получим
(8.46)
Наконец,
при
k + n = k
(или
n =
О)
запишем
Аналитическое
решение
уравнения
(8.31)
можно
отыскать
в
виде
y(k) =
YCB(k)
+
YB(k).
(8.48)
Выражение
(8.48)
содержит
вынужденную
составляющая
YB(k),
соответствующую
реакции
системы
на
входное
воздействие
u(k),
и
свободную
составляющую
YCB(k),
соответствующую
решениям
однородного
разностного
уравнения
(8.40)
при
на
чальных
условиях
у(О),
У(
-1),
...
,
У(
-n
+
1).
Поведение
автономной
системы
и
свободная
составляющая
переходного
процес
са
YCB(k)
зависят
от
полюсов системы
Zi,
которые
в
общем
случае
представлены
комплексно-сопряженными
парами:

252
Глава
8.
Дискретные
системы
или,
в
показательной форме,
-
(8.49)
где
M
i
I
Z
i,i+ll
=
VO!~
+
/3;,
(8.50)
Фi
{Зi
(8.51)
arg
Zi,i+l
=
arctg
-.
O!i
Для
случая
неравных
полюсов
свободная
составляющая
определяется
выражени-
ем:
(8.52)
где
C
i
-
неопределенные
коэффициенты,
зависящие
от
начальных
условий.
Вещественному
неотрицательному
корню
Zi,
для
которого
O!i
~
О,
/3i
=
О,
а
Фi
=
О
соответствует
апериодическая
составляющая
переходного
процесса
(мода)
Yi(k) =
Cilail
k
= C
i
M
i
k
,
а
вещественному
отрицательному
корню,
для
которого
ai
<
О,
{Зi
=
О,
а
Фi
=
7г
-
колебательная
мода
Yi(k) = Ci/ai/
k
= C
i
M
i
k
соsk7Г
(см.
8.1.4
и
рис.
8.11).
Паре
комплексно-сопряженных
корней
характеристического
полиНома
Zi,i+l
соответствует
колебательная
составляющая
(см.
8.1.4
и
рис.
8.12)
Yi,i+l(k) = A
i
M
i
k
соs(kФi
- 'Pi), (8.53)
где
A
i
,
'Pi
-
параметры,
зависящие
от
начальных
условий.
Если
при
некоторых
начальных
значениях
имеет
место
тождество
Уев
(k) =
у*,
k
~
О,
(8.54)
где
у*
= const,
то
значение
у
=
у*
называется
положением
равновесия
автономной
системы
(8.40).
При
условии,
что
а
n
=1=
О,
находим,
что
единственным
положением
равновесия
рассматриваемой
системы
является
начало
координат
у*
=
о.
Вынужденная
составляющая
переходного
процесса
определяется
входным
воз
действием
u(k).
Наиболее
распространенными
входными
сигналами
дискретных
систем
являются
единичная
импульсная
последовательность
и
дельта-функция
Кронекера.
Переходный
процесс
у
= h(k)
системы
(8.31)
при
нулР.вых
начальных
условиях
у(О)
= ... =
У(
-n
+
1)
=
О и
воздействии
на
ее
вход
единичной
импульсной
последовательности
l(k)
=
{~
при
при
k <
О,
k~O
8.1.
Дискретные
модели
динамических
процессов
253
1(k)
1111111111111111111111
8(k)
11
I I I I I I I I
О
2 4 6 8
10
12
14
1618 k
024
6 8 1012
14
16 18
k
h(k)
1111111111111111111111
w(k)
11
I
.1111111111111111111.
о
2 4 6 8
10
12 14
1618 k
О
2 4 6 8 1012
14 16
18
k
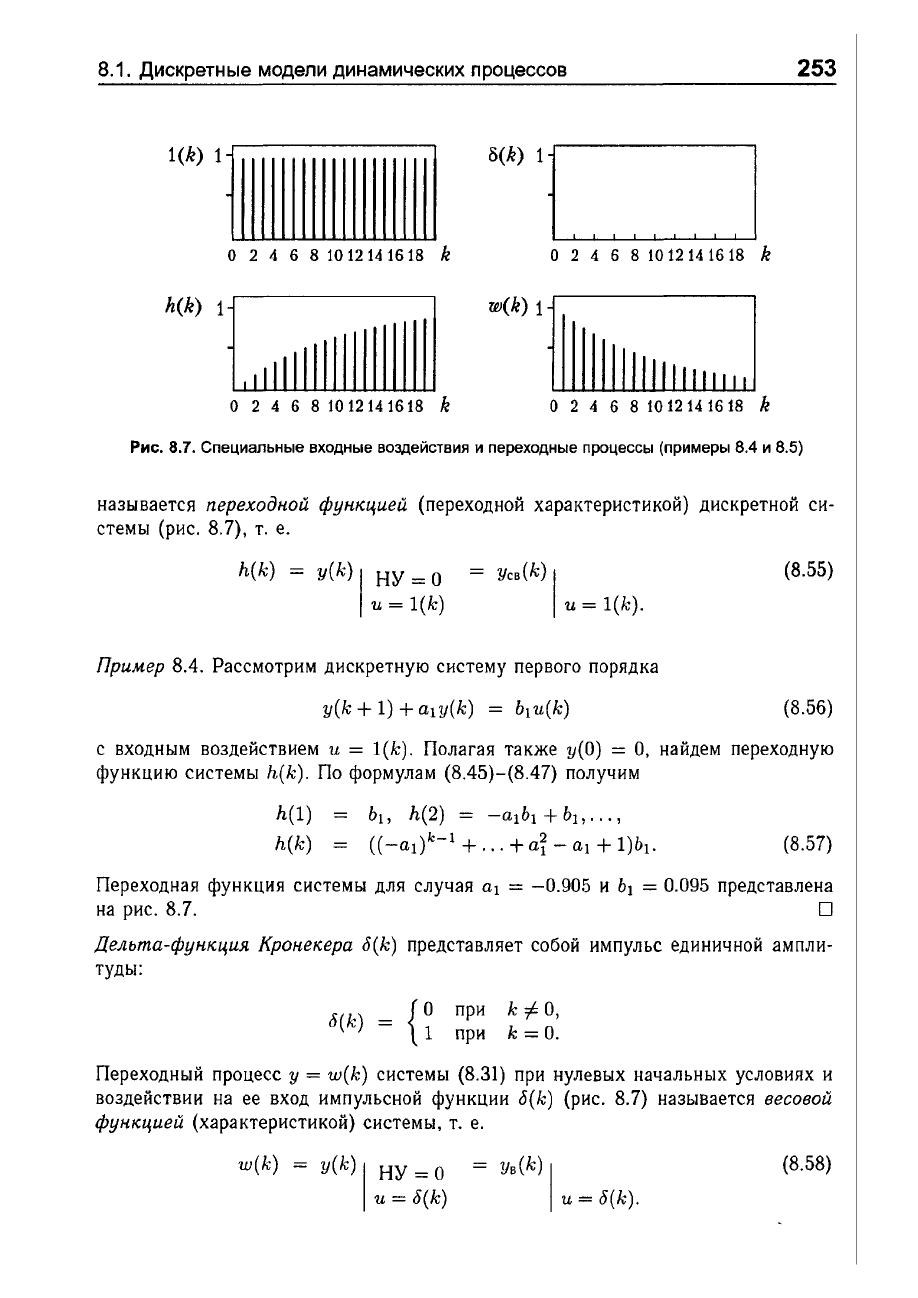
Рис.
8.7.
Специальные
входные
воздействия
и
переходные
процессы
(при
меры
8.4
и
8.5)
называется
переходной
функцией
(переходной
характеристикой)
дискретной
си
стемы
(рис.
8.7),
т.
е.
h(k) = y(k) 1
НУ
=
О
и
=
l(k)
=
YCB(k)
1
и
=
l(k).
Пример
8.4.
Рассмотрим
дискретную
систему
первого
порядка
y(k +
1)
+
aly(k)
=
Ь
1
u(k)
(8.55)
(8.56)
с
входным
воздействием
и
=
l(k).
Полагая
также
у(О)
=
О,
найдем
переходную
функцию
системы
h(k).
По
формулам
(8.45)-(8.47)
получим
h(l)
Ь
1
,
h(2) =
-аlЬl+Ьl,
...
,
h(k) =
((
-al)k-l
+ ... +
a~
-
аl
+
1)Ь
1
•
(8.57)
Переходная
функция
системы
для
случая
аl
=
-0.905
и
Ь
1
= 0.095
представлена
на
рис.
8.7.
О
Дельта-функция
Кронекера
o(k)
представляет
собой
импульс
единичной
ампли
туды:
o(k) =
{О
при
k
=1
О,
1
при
k =
О.
Переходный
процесс
у
= w(k)
системы
(8.31)
при
нулевых
начальных
условиях
и
воздействии
на
ее
вход
импульсной
функции
o(k)
(рис.
8.7)
называется
весовой
функцией
(характеристикой)
системы,
т.
е.
w(k) = y(k) 1
НУ
=
О
и
= o(k)
=
YB(k)
I
(8.58)
и
= o(k).

254
.
Глава
8.
Дискретные
системы
Отметим,
что
по
определению
w(O)
= ... = w(
-n
+
1)
=
О.
Весовая
функция
дискретной
системы
легко
рассчитывается
по
рекуррентной
фор
муле
(8.47).
Принимая
во
внимание
свойства
дельта-функций,
получим:
w(l)
=
Ь
1
0(0)
=
Ь
1
,
(8.59)
w(2) =
-alw(l)
+
Ь
2
0(0)
=
-аlЬl
+
Ь
2
,
.••
, (8.60)
w(k) =
-alw(k
-
1)
-
...
+
ak-lw(l)
+
bko(O).
(8.61)
Пример
8.5.
Рассмотрим
дискретную
систему
первого
порядка
(8.56)
с
входным
воздействием
и
= o(k)
и
начальным
значением
у(О)
=
О.
По
формулам
(8.59)-
(8.61)
получим
w(l)
=
Ь
1
,
w(2) =
-аlЬl,,,,,
w(k) =
(-al)k-
1
b
1
•
(8.62)
Весовая
функция
системы
для
случая
аl
=
-0.905
и
Ь
1
= 0.95
представлена
на
рис.
8.7.
О
Кроме
основной
дельта-функции
Кронекера
известны
также
смещенные
дельта
функции
Oi(k), i =
1'2'
....
Обозначим
oo(k) = o(k)
и
определим
(для
i = 1,2,
...
)
о.
(k) =
о
(k _ i) =
{О
при
k
=1
~,
z
О
1
при
k = 1,.
Реакцией
системы
на
смещенную
дельта-функцию
будет
смещенная
весовая
ФУНК
ция
(рис.
8.8)
(8.63)
где
wa(k) = w(k).
11.~~,
,
,1
,~i"
, , ,
'"
, , 1
1
1.",
]111111111111
о
k
О
k
Рис.
8.8.
Смещенные
импульсные
функции
По
известным
весовым
ФУНКЦИЯ'ММОЖ~i
быть
определена
реакция
системы
на
про
извольное
входное
воздействие,
т.
е.
найдена
вынужденная
составляющая
переход
ного
процесса
ys(k).
Представим
дискретное
воздействие
u(k)
в
виде
разложения
по
дельта-функциям:
u(k) = u(O)oo(k) + U(l)Ol(k) + ... + U(i)Oi(k) + ....

8.1.
Дискретные
модели
динамических
процессов
Получим
YB(k)
= u(O)wo(k) +
u(l)Шl(k)
+ ... + U(i)Wi(k) + ...
и,
учитывая
свойство
(8.63),
найдем
k-i
уз(k)
= L w(k -
l)u(i).
i=O
255
(8.64)
Формула
иногда
называется
суммой
свертки
и
аналогична
интегралу
свертки
(2.62).
По
формуле
(8.64)
нетрудно
определить
переходную
функцию
дискретной
системы
k-l
h(k) = L w(k - 1).
(8.65)
i=O
Установившийся
режим.
Рассмотрим
поведение
модели
ВВ
при
постоянном
вход
ном
воздействии
и(
k)
==
const
и
установившуюся
составляющую
переходного
про
цесса
У
=
Уу
==
const.
Замечая,
что
в
установившемся
(статическом)
режиме
для
любых
i
~
О
выполняется
Yy(k
+ i) =
Уу
и
u(k + i) = u(k),
из
выражения
(8.31)
находим
статическую
характеристику
дискретной
системы:
Ь
1
+ ... +
Ь
n
К
Уу
= u =
и,
1 +
аl
+ ... +
а
n
(8.66)
где
К
-
статический
коэффициент.
Отметим,
что
условием
существования
ста
тической
характеристики
является
1 +
аl
+ ... +
а
n
f.
О,
и
система,
удовлетворяющая
этому
условию,
называется
статической.
Статическая
характеристика
может
быть
получена
также
из
операторной
формы
(8.33)
или
(8.38).
Сопоставляя
(8.66)
и
(8.38).,
найдем
Ь
1
+ ... +
Ь
n
=
W(l)
=
а
Ь
«ll))'
(8.67)
1 +
аl
+ ... +
а
n
Следовательно,
W(l)
=
К,
и
в
статическом
режиме
система
описывается
уравне-
нием
Уу
=
W(l)u.
(8.68)
8.1.3.
Модели
вход-состояние-выход
Сначала
проанализируем частный
случай
управляемой
дискретной
системы,
опи
сываемой
уравнением
y(k
+ n) +
aly(k
+ n -
1)
+ ... + a
n
-ly(k
+
1)
+ any(k) = bu(k).
(8.69)

256
Глава
8.
Дискретные
системы
Введем
в
рассмотрение
переменные
состояния
хl
(k) y(k),
x2(k)
= y(k + 1),
(8.70)
xn(k)
y(k+n-1)
с
начальными
значениями
Хl(О)
=
у(О),
Х2(О)
=
у(l),
...
,
хn(О)
=
у(n
- 1).
Используя
выражения
(8.69)
и
(8.70),
найдем
уравнения
состояния
-
систему
n
разностных уравнений
первого
порядка
вида
= x2(k),
=
хз(k),
При
этом
уравнение
выхода
имеет
вид
(8.71)
(8.72)
Структурная
схема
полученной
модели
(рис.
8.9)
строится
с
использованием
опера
торов
сдвига
(запаздывания)
1/
z,
связывающих
два
соседних
значения
переменной
х
по
правилу
1
x(k) = - x(k + 1).
z
Уравнения
(8.71)-(8.72)
представляют
собой
простейший
случай
модели
вход
состояние-выход
(ВСВ).
В
более
общем
случае
модель
ВСВ
управляемой
дис
кретной
системы
содержит
уравнения
состояния
вида
z
Рис.
8.9.
Структурная
схема
дискретной
системы
(частный
случай)
8.1.
Дискретные
модели
динамических
процессов
257
xl(k
+
1)
=
allXl(k)
+
a12
X
2(k) + ... + alnxn(k) + b1u(k),
x2(k +
1)
= a21Xl(k) +
a22X2(k)
+ ... + a2nxn(k) + b
2
u(k),
(8.73)
и
уравнение
выхода
(8.74)
где
aij,
b
i
,
Ci -
постоянные
или
зависящие
от
времени
коэффициенты
(парамет
ры).
Модель
(8.73)-(8.74)
связывает
вход
u(k)
и
выход
y(k)
через
промежуточные
переменные
Xi(k).
Для
преобразования
модели
к
компактной
векторно-матричной
форме
необходимо
определить
вектор
состояния
Х
=
{Xi}
Е
JRn,
а
также
матрицы
А
=
{Щj},
в
=
{b
i
}
и
С
=
{Ci},
i =
1,n.
Тогда
уравнения
(8.73)-(8.74),
описывающие
модель
вход
состояние-выход,
принимают
вид:
x(k
+ 1) -
Ax(k)
+
Bu(k),
y(k)
-
Cx(k),
где
х(О)
=
Хо.
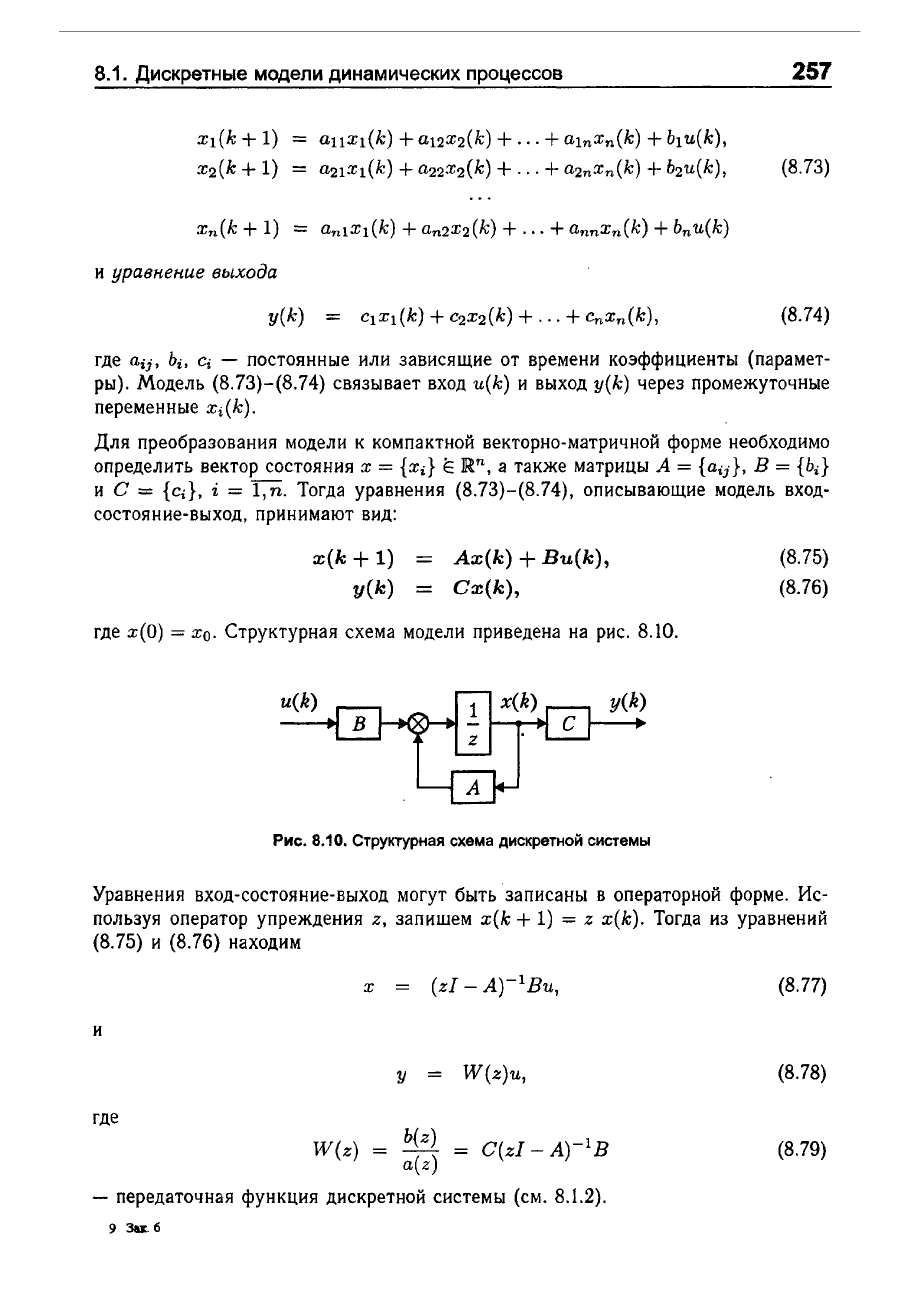
Структурная
схема
модели
приведена
на
рис.
8.10.
Рис.
8.10.
Структурная
схема
дискретной
системы
(8.75)
(8.76)
Уравнения
вход-состояние-выход
могут
быть
'записаны
в
операторной
форме. Ис
пользуя
оператор
упреждения
z,
запишем
x(k
+
1)
= z x(k).
Тогда
из
уравнений
(8.75)
и
(8.76)
находим
и
где
Х
=
(zI
-
A)-l
Ви,
у
=
W(z)u,
W(z)
= b(z) =
C(zI
-
A)-l
В
a(z)
-
передаточная
функция
дискретной
системы
(см.
8.1.2).
9
З
•.
6
(8.77)
(8.78)
(8.79)

258
Глава
8.
ДискреТНblе
системы
Нетрудно
получить,
что
a(z) =
det(zI
-
А)
(8.80)
и,
следовательно,
полюсы
системы
zi
(корни
характеристического
полинома
a(z))
совпадают
с
собственными
числами
матрицы
А:
(8.81)
Автономная
модель дискретной
системы
является
частным
случаем
модели
ВСВ
(8.75)-(8.76)
в
отсутствие
входных
воздействий:
и
=
о.
Она
принимает
вид
x(k
+ 1) -
Ax(k),
y(k)
-
Cx(k).
(8.82)
(8.83)
Аналогично
получаются
модели
ВСВ
многоканальных
систем,
а
также
модели
возмущенных
дискретных
систем,
на
входы которых
поступают
дополнительные
импульсные
сигналы
(возмущающие
воздействия).
В
простейшем
частном
случае
уравнения
состояния
возмущенной
системы
прини
маюТ
вид
(8.84)
в
более
общем
случае
возмущенная
дискретная
система
может
быть
представлена
в
векторно-матричной
форме,
содержащей
уравнение
состояния
x(k
+ 1) =
Ax(k)
+
Bu(k)
+
Df(k)
(8.85)
и
уравнение
выхода
(8.76).
Решение
разностных
уравнений.
Рассмотрим
решения
уравнений
(8.75)-(8.76),
полагая
k
2::
о.
Рекуррентное
решение
получается
непосредственно
из
выражения
(8.75).
При
k =
О,
запишем
х(О)
=
ха
и
у(О)
=
Схо.
Далее,
при
k = 1
получим
х(1)
=
Ах(О)
+
Вu(О),
у(1)
=
Сх(1),
при
k = 2 -
х(2)
=
Ах(1)
+
Вu(1),
у(2)
=
Сх(2),
при
k = i -
x(i)
=
Ax(i
-
1)
+
Bu(i
- 1),
y(i)
=
Cx(i)
и
т.
д.
Решение
соответствует
итерационной
процедуре,
на
каждом
шаге
которой
k = i
используются
значения
x(i
-
1),
найденные
на
предыдущем
шаге
итерации.

8.1.
Дискретные
модели
динамических
процессов
259
Для
нахождения
аналитического
решения
уравнения
состояния
(8.75)
в
рассмот
ренной
выше
процедуре
осуществим
соответствующие
подстановки.
Найдем
х(l)
Ахо
+
Вu(О),
х(2)
=
А
2
х(о)
+
АЬu(О)
+
Ьu(1),
.
..
и,
наконец,
k-l
x(k) =
xcB(k)
+
xB(k)
= Akxo + L A
k
-
i
-
1
Bu(i),
(8.86)
i=O
где
xcB(k)
-
свободная
составляющая
вектора
состояния
(или
состояние
авто
ноМной
системы
(8~82)-(8.83»,
xB(k)
-
вынужденная
составляющая
(реакция
на
входное
воздействие
u(k».
Подставляя
(8.86)
в
уравнение
выхода
(8.76),
получаем
аналитическое
выражения
для
расчета
выходной
переменной
k-l
y(k) =
YCB(k)
+
YB(k)
'CAkxo + L
CA
k
-
i
-
1
Bu(i).
(8.87)
i=O
Решение
(8.87)
может
быть
представлено
как
k-l
y(k) =
СФ(О,
k)xo + L w(k -
i)u(i),
(8.88)
i=O
где
Ф(О,
k) = A
k
(8.89)
-
фундаментальная
(nереходная)
матрица
дискретной
системы,
а
w(k) =
СФ(О,k-1)В
=
CAk-1в
(8.90)
-
ее
весовая
функция
(см.
8.1.2).
При
этом
выражение
для
расчета
вынужденной
составляющей
процесса
YB(k)
совпадает
с
приведенной
ранее
формулой
(8.64).
Свойства
моделей.
Сначала
рассмотрим
поведение
автономной
модели
(8.82)-
(8.83)
и
решения
x(k)
y(k)
Если
для
х(О)
=
х*
и
любых
k
2::
О
имеет
место
тождество
x(k) =
х*,
(8.91)
(8.92)
то
значение
х
=
х*
называется
равновесным
состоянием, или
положением
равно
весия,
автономной
системы.
Очевидно,
что
в
равновесном
состоянии
выполняется
x(k +
1)
= x(k)
(8.93)
