Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.


Глава
8.
Дискретные
системbI
Как"
11
'в'
слу*-Iае
непрерывных
систем,
понятия
устойчивости
по
выходной
пере
мен
ной
и
вектору
состояния
совпадают
при
условии
полной
наблюдаемости
рас
сматриваемой
дискретной
системы.
Для
неполностью
наблюдаемых
систем
из
устойчивости
по
выходу,
вообще
говоря,
не
следует
устойчивость
по
состоянию
(см.
[26]).
, ,
О~но~~о,й
M,e~oд
исследования
устойчивости
дискретных
системы
предусматривает
использование
корневых
критериев.
Рассмотрим
решения
уравнения
(8.129)
для
неравных
корней
Zi
(см.
8.1.2):
n n
y(k)
=
LYi(k)
= L
Cizf·
(8.135)
i=l i=l
Напомним,
что
корню
характеристического
полинома
zi
(вещественному
или
ком
плексному)
с
модулем
M
i
и
аргументом
'1А
соответствует
составляющая
переход
ного
процесса
(мода)
. "
(8.136)
При
условии,
что
модуль
M
i
строго
меньше
единицы,
т.
е.
(8.137)
соответствующая
составляющая
переходного
процесса
Yi(k)
со
временем
затухает.
Если
условие
(8.137)
имеет
место
для
всех
корней
zi (i =
г,n),
то
затухающей
является'
и
функция
y(k)
в
целом,
т.
е.
выполняется
условие
асимптотической
устойчивости
(8.134).
Аналогичный
результат
получается
при
рассмотрении
поведения
вектора
x(k)
как
решен'ия
уравнения
(8.130): '
x(k) = A
k
ха.
(8.138)
Переходя
к
нормам,
получаем
Ix(k)1
<
IAl
k
IXal,
(8.139)
где
(8.140)
Следовательно,
lim
Ix(k)1
=
'Хаl
Нm
IAl
k
.
k-->oo k-->oo
(8.141)
.
~
в
силу
определения
/А/
получаем,
что
необходимым
и
достаточным
условием
аСИМ(1ТОТl(lческой
устойчивости
(8.130)
будет
Лi{АТ
А}
<
1,
или,
что
эквивива
лентно,
/Лi{А}/
<
1.
Таким
образом,
справедлива
следующая
формулировка
(корневой
критерий).

8.3.
Качество
дискретных
систем
управления
271
Свойство
8.5.
Дискретная
полностью
наблюдаемая
система
(8.129)
или
(8.130)-
(8.131)
асимnтотически
устойчива
тогда
и
только
тогда.
когда
выполняется
усло-
вие
1т
z
Re
z
(8.142)
Критерий
связывает
понятие
асимптотической
устой
чивости
с
размещением
корней
характеристического
полинома
на
комплексной
'1ло<;кости:
расположение
всех
корней
внутри
круга
еДиничного
радиуса
экви
валентно
асимптотической
устойчивости
системы.
По
этому
окружность
единичного
радиуса
является
гра
ницей
устойчивости.
Нетрудно:
показать.
что
наличие
хотя
бы
одного
корня
Zi
= z*
вне
единичного
круга.
т.
е.
Iz*1
>
1,
делает
дискретную
систему
неустоЙчивоЙ.
Появление
одного
вещественного
или
пары двух
комплексно-сопряженных
корней
на
единичной
оkРУЖНQСТИ
Iz*1
= 1
при
условии
расположения
остальных
корней
внутри
круга
говорит
о
нейтральной
устойчивости
дискретной
системы
(УСТОЙЧJ:'lвости
по
Ляпунову).
3амечение
8.2.
Корневые
критерии
устойчивости
дискретных
систем
могут
быть
легко
выведены
из
соответствующих
положений
непрерывной
теории
(см.
5.2.2),
если
принять
во
внимание,
что
полюсы
Zi
дискретной
системы
связаны
с
полюса
ми
Pi
эквивалентной
непрерывной
модели
соотношениеМ
Zi';:::
exp(Tpi)
(свойство
8.1.
см.
8.1.1).
Это
свойство
широко
используется
для
анализа
динамических
по
казателей
качества
дискретных
систем.
8.3.
Качество
дискретных
систем
управления
Как
и
для
систем
непрерывного
времени
показатели
качества
дискретных
систем
предназначены,
во-первых.
для
оцеНЮi
динамических
свойств
системы.
проявляю
щихся
в
переходных
режимах,
и,
во-вторых,
для
определения
точности.
характе
ризующейся
ошибками
системы
в
установившемся
режиме
а
.1'.
е.
после
окончания
переходных
процессов.
8.3.1.
Динамические
показатели
качества
Динамические
показатели
характеризует
поведение
свободных
составляющих
пе
реходного
процесса
YCB(k)
или
xcB(k)
замкнутой
сисtемы
управления,
либо.
про
цессов
автономной
системы.
Последние
рассматриваются
как
решения
скалярного

Глава
8.
Дискретные
системы
разностного
уравнения
или
модели
состояние"выход
x(k
+
1)
= Adx(k),
y(k) = Cdx(k)
с
характери.стическим
полиномом
ad(Z)
И
полюсами
Zi
= Ai{A
d
},
i =
1,
n.
(8.143)
(8.144)
(8.145)
Естественно,
что
рассматриваются
только
устойчивые
системы
и,
следовательно,
выполняется
условие
(8.142).
.
Динамические
показатели
качества
дискретных
систем
определяются
аналогично
показателям
систем
непрерывного
времени
и
могут
быть
найдены
с
использовани
ем
тех
же
подходов
(см.
п.
6.1-6.2).
Однако
в
силу
того,
что
в
основе
дискретных
моделей
часто
лежат
процессы
непрерывной
природы
(см.
8.1.1),
более
целесообраз
но
установить
соотношениями
между
динамическими
показателями
дискретных
и
непрерывных
систем.
Такие
соотношения
получаются
на
основе
конформных
отоб
ражений
комплексных
переменных
[10,
12].
В
общем
случае
к
классу
конформных
относятся
отображения
комплексных
переменных,
сохраняющие
величины.
углов
между
пересекающимися
кривыми
(рис.
8.13).
Imz
в'
А
o----~
о
Rep
о
Rez
D
с
Рис.
8.13.
Конформное
отображение
Будем
полагзть,
что
дискретная
система
получена
в
результате
дискретизации
динамической
системы
непрерывного
времени,
которая
описывается
скалярным
уравнением
a(p)y(t) =
О
или
уравнениями
состояние-выход
x(t) =
Ax(t),
y(t) =
Cx(t).
(8.146)
(8.147)
(8.148)

8.З.
Качество
дискретных
систем
управления
273
Асимптотически
устойчивая
непрерывная
система
имеет
характеристический
по
лином
а{р)
И
полюсы
где
,сч
>
О,
{Зi
~
О.
Напомним
(см.
8.1.~
и
свойство
8.1),
что
Cd
=
С,
матрицы
А
и
A
d
связаны
соот
ношением
(8.149)
а
значения корней
характеристических
полиномов
(полюсов)
дискретной
и
непре
рывной
систем
-
выражением
в
силу
последнего
выполняются
следующие
соотношения:
Zi
=
e-ОiТ(СОS{ЗiТ=fjsiП{Зi
Т
),
а
также
argzi
(8.150)
(8.151)
(8.152)
(8.153)
(8.154)
Для
выбора
интервала
квантования
Т
при
переходе
к
дискретной
форме
описания
принимается
во
внимание
условие
(8.112)
теоремы
прерывания
(см.
8.1.1).
Найдем
значение
{З*
=
m~{Зi,
i =
1,
n,
~
соответствующее
наибольшей
частоте
колебательных
составляющих
переходных
процессов
непрерывной
системы.
По
теореме
прерывания
интервал
квантования
должен
удовлетворять
условию
т
<
1г
{З*
.
(8.155)
Поэтому
в
дальнейшем
будем
полагать,
что
для
полюсов
непрерывной
системы
выполняется
1г
11т
Pil
~
{З*
<
Т'
(8.156)
Условие
(8.156)
с
одной
стороны
отвечает
требования
теоремы
прерывания,
а
с
другой,
в
силу
Т{Зi
<
1г
И
выражения
(8.154),
вводит
ограничение
на
аргументы
полюсов
дискретной
системы.
10
Зак.
6

274
Глава
8.
Дискретные
сиотемы
Свойство
8.6.
Полюсы
Zi
дискретной
системы
удовлетворяют
условию
largzil
<
7Г,
i=l,n,
(8.157)
тогда
и
только
тогда,
когда
полюсы
Pi
соответствующей
непрерывной
системы
подчиняются
условию
(8.156).
Отметим,
что
свойство
8.6
устанавливает
условие
взаимно-однозначного
соответ
ствия
между
полюсами
непрерывной
и
дискретной
систем,
связанными
соотноше
нием
(8.150).
Комлекснозначная
функция
(8.158)
определяет
конформное
отображение
комплексных
чисел
и
ставит
в
соответствие
значениям
полюсов
непрерывной
системы
полюсы
эквивалентной
дискретной
си
стемы
(см.
рис.
8.13).
При
этом
неравенства
(8.156)
и
(8.157)
устанавливают
обла
сти
комплексной
плоскости,
в
которых
отображение
(8.158)
взаимно-однозначно.
Это
и
служит
формальным
обоснованием
возможности
проведения
анализа
дина
мических
показателей
дискретных
системы
на
основе
известных
свойств
систем
непрерывного
времени
(см.
п.
6.2).
Отметим
{)сновные
свойства
функции
(8.158)
(рис.
8.14).
1.
Кусок
левой
полуплоскости,
ограниченный
прямыми
Imp
=
~{З*,
где
{З*
=
==
7ГТ,
т.
е.
область
р-
{р:
Re
р
~
О,
11т
pl
<
{З*}
отображается
в
область
z- =
{z:
Izl~l
\
(Rez<O,jO)},
т.
е.
в
круг
единичного
радиуса,
из
которого
исключена
левая
вещественная
полуось
(Re z < O,jO).
13*
Тр
z=e
====>
О
z
SO
О
Rep
-1
1
Re
z
-13*
LO
Рис.
8.14.
Свойства
отображения
(8.158)

8.3.
~ечество
дискретных
систем
управления
275
2.
Отрезок
мнимой
оси,
ограниченный
точками
1т
р
=
~{З*,
т.
е.
вО
=
{р:
Re
р
=
О,
11т
рl
< f3*}
отображается
в
кривую
L
O
=
{Z:
Izl
= 1 \
(-l,jО)},
т.
е.
в
окружность
единичного
радиуса,
из
которой
исключена
точка
(-1,
jO).
3.
Точка
рО
=
(O,jO)
отображается
в
точку
zO
=
(1,
-jО).
4.
Бесконечно
удаленная
точка
левой
вещественной
полуоси
рОС
=
(-00,
jO)
отображается
в
центр
круга
z- -
точку
ZOC
= (O,jO).
5.
Граничные
точки
(О,
-=fjf3*)
отрезка
ВО
отображаются
в
точку
(-l,jО).
Перечисленные
свойства
сразу
же
позволяют
сделать
вывод
об
аСИМП1'отиче
кой
устойчивости
дискретной
системы,
полюсы
которой
лежат
внутри
единичной
окружности
(см.
свойство
8.5).
Более
подробный
анализ
отображения
различных
областей
расположения
полюсов
приводит
к
оценкам
качественных
показателей
дискретной
системы,
рассмотренным
ниже.
Оценка
быстродействия.
Прежде
всего
отметим,
что
скорость
протекания
дис
кретных
процессов
определяется
значениями
модулей
полюсов
системы
IZil.
Дей
ствительно,
выражение
(8.153)
показывает,
что
значения
IZil
уменьшаются
с
уве
личением
модулей
вещественных
частей
полюсов
непрерывной
системы
ai,
ЧТО
по
теореме подобия
(свойство
6.1,
6.2.1)
равносильно
увеличению
быстродействия,
т.
е.
уменьшению
времени
переходного
процесса
t
n
.
Более
того,
в
соответствии
со
свойством
8.2
в
случае,
когда
дискретная
система
имеет
только
нулевые
полюсы
Zi
=
Лi{А
d
}
=
О,
i =
г,n,
ее
переходный
процесс
заканчивается
не
более
чем
за
n
шагов,
и,
следовательно,
время
переходного
процесса
определяется
выражением
t
n
~
nТ.
(8.159)
Отмеченное
выше
обстоятельство
служит
основанием
для
введения
(по
аналогии
с
понятием
степени
устойчивости
непрерывных
систем,
см.
6.2.2)
понятия
степе
ни
устойчивости
дискретной
системы
как
радиуса
распределения
ее
полюсов
на
комплексной
плоскости.
Степенью
устойчивости
дискретной
системы
называется
положительное
число
7J
=
т~x
IZil,
i =
1,
n.
(8.160)
~
Учитывая,
что
скорость
протекания
процессов
возрастает
при
приближении
по
люсов
к
началу
координат
(О,
jO),
можно
заключить,
что
степень
устойчивости
276
Глава
8.
Дискретные
системы
Imp
Тр
z=e
====>
Imz
1
1
Rez
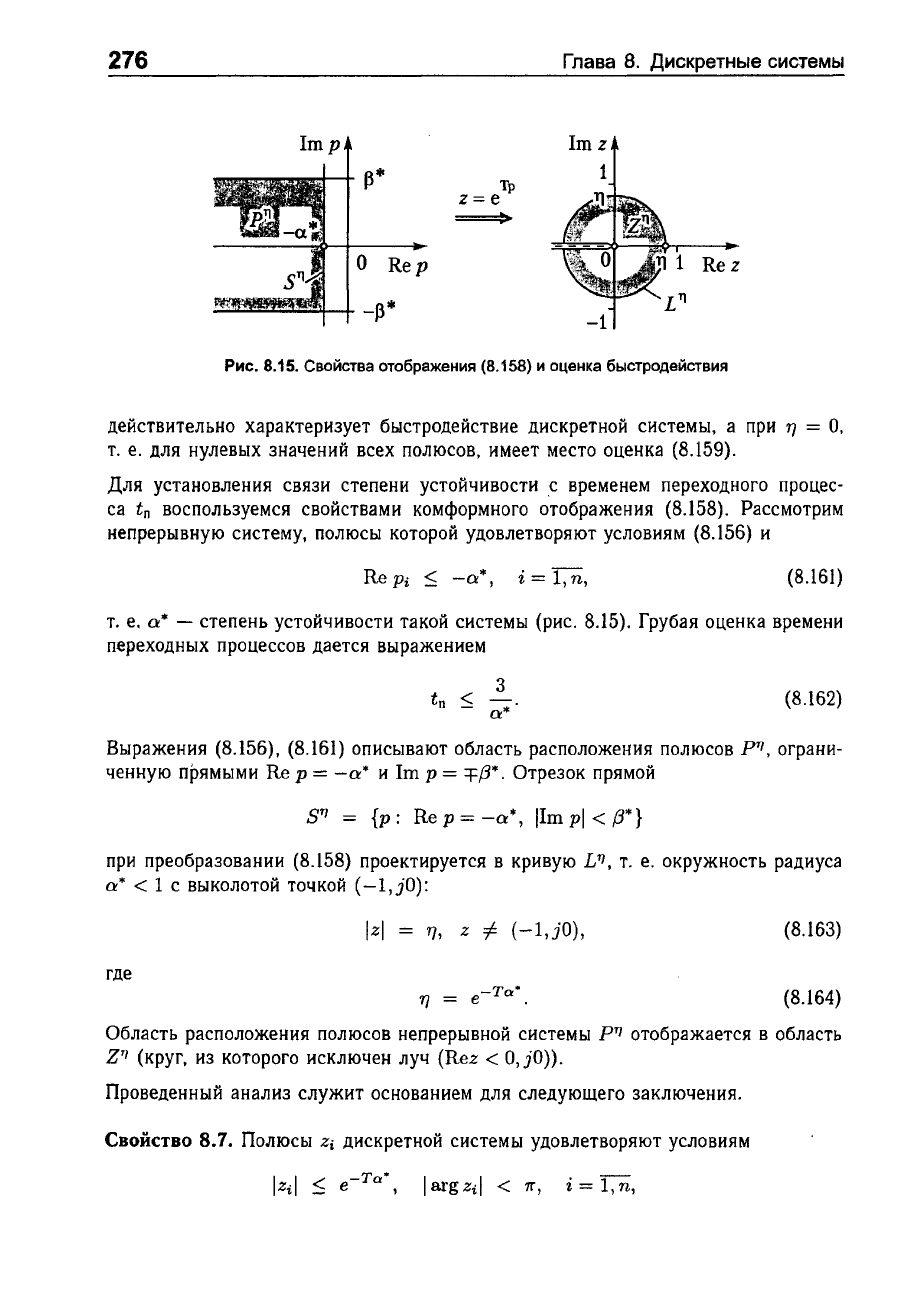
Рис.
8.15.
Свойства
отображения
(8.158)
и
оценка
быстродействия
действительно
характеризует
быстродействие
дискретной
системы,
а
при
7]
=
О,
т.
е.
для
нулевых
значений
всех
полюсов,
имеет
место
оценка
(8.159).
Для
установления
связи
степени
устойчивости
.с
временем
переходного
процес
са
t
л
воспользуемся
свойствами
комформного
отображения
(8.158).
Рассмотрим
непрерывную
систему,
полюсы
которой
удовлетворяют
условиям
(8.156)
и
Re
Pi
~
-а*,
i = 1,n,
(8.161)
т.
е.
а*
-
степень
устойчивости
такой
системы
(рис.
8.15).
Грубая
оценка
времени
переходных
процессов
дается
выражением
3
t
л
<
-.
-
а*
(8.162)
Выражения
(8.156),
(8.161)
описывают
область
расположения
полюсов
рт7,
ограни
ченную
прямыми
Re
Р
=
-а*
и
1т
Р
=
=F{З*.
Отрезок
прямой
Вт7
=
{р:
Re
Р
=
-а*,
11т
рl
<
{З*}
при
преобразовании
(8.158)
проектируется
в
кривую
Lry.
т.
е.
окружность
радиуса
а*
< 1
с
выколотой
точкой
(-1,jО):
Izl
=
7],
z
=j;
(-1,
jO),
(8.163)
где
(8.164)
Область
расположения
полюсов
непрерывной
системы
рт7
отображается
в
область
Zry
(круг,
из
которого
исключен
луч
(Rez < O,jO).
Проведенный
анализ
служит
основанием
для
следующего
заключения.
Свойство
8.7.
Полюсы
Zi
дискретной
системы
удовлетворяют
условиям
-То"·
е
,
i = 1,n,

8.3.
Качество
дискретных
систем
управления
277
тогда
и
только
тогда,
когда
полюсы
Pi
эквивалентной
непрерывной
системы
удо
влетворяют
неравенствам
(8.156)
и
(8.161).
Из
выражения
(8.164)
находим
значение
а*,
и
после
его
подстановки
в
(8.162)
получаем
3Т
t
<--
л
- ln
7]'
(8.165)
что
соответствует
грубой
оценке
времени
переходных
процессов
дискретной
систе
мы
с
радиусом
распределения
корней
(степенью
устойчивости)
7].
Оценка
КОJlебатеJlЬНОСТИ.
Напомним,
что
колебательность
непрерывных
систем
связана
с
наличием
комплексно
сопряженных
полюсов.
Для
устойчивой
системы
с
вещественными
полюсами,
т.
е.
при
Pi
=
-ai
<
О,
все
составляющие
переходного
процесса
имеют
апериодический
характер.
При
преобразовании
(8.158)
область
расположения
таких
полюсов
(левая
вещественная
полуось
Rep <
О)
проектируется
в
единичный
отрезок
правой
вещественной
полуоси:
О
::;
Re
Z <
1.
Следовательно,
условием
получения
устойчивых
апериодических
процессов
дискретной
системы
будет
О
::;
Rezi
<
1,
Imzi =
О.
ДЛЯ
других
значений
полюсов
из
внутренности
единичного
круга
переходные
про
цессы
носят
колебательный
характер.
Колебательность
процессов
непрерывной
системы
можно
оценить
с
помощью
по
казателя
затухания
~
(см.
6.2.3),
который
связан
с
размещением
полюсов
на
ком
плексной
плоскости.
Показатель
/
1т
Р
'/
(
(з,
)
l1=m?X-
R
t=m?X-2.,
t
е
Pi
t
ai
i = 1,n,
(8.166)
называемый
степенью
колебательности,
связан
с
размером
сектора
рр.
(рис.
8.16),
в
котором
расположены
все
полюсы
системы,
по
формуле
ф
=
arctg
11,
а
значение
показателя
затухания
находится
как
~
= 1 -
e-
27r
/J1-.
(8.167)
Для
установления
связи
степени
колебательности
11
с
расположением
корней
дис
кретной
системы
воспользуемся
свойствами
комформного
отображения
(8.158).
Рассмотрим
асимптотически
устойчивую
непрерывную
систему,
полюсы
которой
удовлетворяют
условиям
(8.156)
и
1
1т
Pi/
Re
Pi
::;
11,
(8.168)
т.
е.
расположены
в
секторе
рр.
(см.
рис.
8.16).

278
Глава
8.
Дискретные
системы·
Imp
1т
z
о
Rep
Тр
z=e
====>
'"
Рис.
8.16.
Свойства
отображения
(8.158)
и
оценка
колебательности
Отметим,
что
в
силу
свойства
сохранения
углов
область
расположения
полюсов
эквивалентной
дискретной
системы
ZJ1-
лежит
в
пределах
сектора
размера
2'Ф.
Рас
смотрим
лучи
в+
И
в-
сектора
рр.
(см.
рис.
8.16).
Их
описание
дается
выражением
1т
Р
=
±J.l
Re
р,
Re
р
<
О
или,
в
параметрической
форме,
-
р
=
-0(1
~
jJ.l),
о
Е
(0,00).
(8.169)
Подставляя
последнее
выражение
в
(8.150),
получаем
параметрическое
описание
кривых
L +
и
L -
на
комплексной
плоскости
дискретной
системы:
(8.170)
Найденные
кривые
L +
и
L -
ограничивают
обл.асть
ZJ1-,
в
которой
расположены
ПОJIЮСЫ
дискретной
системы,
соответствующие
степени
колебательности
J.l.
Если,
кроме
того,
полюсы
непрерывной
системы
удовлетворяют
неравенству
(8.156),
то
нетрудно
показать,
что
пара
метр
О
ограничивается
значением
1г
/
(J.lT).
Проведенный
анализ
служит
основанием
для
следующего
заключения.
Свойство
8.8.
Полюсы
Zi
дискретной
системы
удовлетворяют
условиям
-ВТ
е
,
i
=
1,n,
(8.171)
где
о
Е
(о,
;т)'
тогда
и
только
тогда,
когда
полюсы
Pi
эквивалентной
непрерывной
системы
удо
влетворяют
неравенствам
(8.156)
и
(8.168).
Значение
показателя
затухания
~,
соответствующего
полюсам
дискретной
систе
мы,
удовлетворяющим
неравенствам
(8.171)
и
лежащим
в
области
ZJ1-,
находится
из
выражения
(8.167).

8.3.
Качество
дискретных
"систем
управления
279
Синтез
дискретных
систем
по
заданным
динамическим
показателям.
Если
в
основе
дискретной
модели
лежит
описание
непрерывного
динамического
процесса
(объекта
управления),
то
постановка
задачи
синтеза
должна
быть
ориентирована
на
получение
желаемых
качественных
показателей
процессов
непрерывного
вре
мени,
к
которым
относится
время
переходного
процесса
t
п
,
перерегулирование
и
или
затухание
~.
Можно
предложить
два
подхода
к
проектированию
такого
рода
дискретных
систем.
Первых
подход
предусматривает
использование
полученных
выше
приближенных
оценок
качества
и
показателей
t
n
,
~.
По
заданным
значениям
этих
показателей
определяются
значения
степени
устойчивости
и
степени
колебательности
а*
=
3
27Г
J.l
=
ln(l/(l
-
~))
(8.172)
(8.173)
системы
непрерывного
времени.
После
вычисления
по
формуле
(8.164)
значения
Т],
определяется
круг
zry,
а
затем
по
формуле
(8.170)
-
границы
области
ZI1-.
Пересечение
Zry
и
ZI1-
дает
искомую
область
расположения
полюсов
дискретной
системы.
После
назначения
полюсов
Zi
Е
ZТ1ПZI1-,
i = 1,n,
расчет
коэффициентов
обратных
связей
регулятора
может
быть
произведен
мето
дом
модального
управления
(см.
7.3.1).
Отметим,
что
формула
(8.162)
дает
лишь
грубую
оценку
оценку
времени
пере
ходного
процесса
и
поэтому
расположение
корней
в
найденной
области
не
всегда
гарантирует
получение
заданного
значения
t
n
•
Второй
подход
к
проектированию
дискретной
системы
позволяет
исключить
ис
пользование
грубых
оценок
времени
переходного
процесса.
Он
предусматривает
нахождение
точных
значений
всех
полюсов
непрерывной
системы
Pi,
обеспечива
ющих
заданное
качество
переходных
процессов,
и
затем
вычисление
соответству
ющих
значений
полюсов
дискретной
системы
Zi
по
правилу
Zi
= exp(Tpi)'
При
этом
полюсы
Pi
определяются
по
заданным
показателям
t
n
и
и
с
помощью
метода
стандартных
переходных
функций
(см.
п.
6.3).
8.3.2.
Оценка
точностных
показателей
Как
и
для
систем
непрерывного
времени
(см.
6.1.3),
точностные
показатели
дис
кретной
системы
управления
оцениваются
по
установившимся
составляющим
пе
реходных
процессов
yy(k)
и
ey(k).
Поведение
конкретной
системы
в
установив
шемся
режиме
зависит
от
ее
структурных
свойств,
значений
параметров,
а
также
