Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.


300
Глава
9.
Цифровые
системы
управления
воспользовавшись
приближенным
описанием
производной
через
прямую
разность.
Полагая
t =
kT,
из
выражения
(9.24)
получим
x(t)
=
x(kT
+
Т)
-
x(kt)
,
Т
и
подставляя
(9.28)
в
(9.26),
найдем
x((k
+
l)Т)
=
(I
+
TA)x(kT)
+
TBu(kT).
Введем
обозначение
и
окончательно
запишем
дискретную
модель
системы
(9.26)-(9.27):
x((k
+
l)Т)
y(kT)
= AdX(kT) + BdU(kT),
Cx(kT).
(9.28)
(9.29)
(9.30)
(9.31)
Рассмотрим
также
задачу
дискретизации
ПИД-регулятора
(см.
п.
7.2),
описывае-
мого
выражением
r
t
dy
u
=
Кру
+
К[
Jo
У(Т)
dT
+ K
D
dt
или,
в
дифференциальной
форме
-
(9.32)
Воспользовашись
приближенным
описанием
первой
производной
через
обратную
разность
(9.25),
получим
i; =
и
и
=
y(kT)
-
y((k
-
l)Т)
Т
u(kT)
-
u((k
-
l)Т
Т
(9.33)
(9.34)
Для
замены
второй
производной
ii
запишем
..
.
i;(kT)-i;((k-l)Т)
у
=
т
y(kT)
- 2y((k -
l)Т)
+
у((А:
-
2)Т)
(9.35)
Т
Подставив
(9.33)-(9.35)
в
уравнение
(9.32),
найдем
разностное
уравнение
пид
регулятора:
u(kT)
=
u((k
-
l)T)
+ K
1
y((kT)
+ K
2
y((k
-
l)Т)
+
Кзу((k
-
2)Т),
(9.36)
где
коэффициенты
K
i
выражаются
через
значения
параметров
Кр,
К[,
KD
И
Т.
Выражение
(9.36)
связывает
текущее
значение
управляющего
воздействия
u(kT)

9.2.
Проблемы
дискретизации
непрерывных
моделей
301
Рис.
9.13.
Алгоритм
ПИД-регулятора
с
его
предшествующим
значением
u((k
-
I)Т)
и
значениями
выходного
воздей
ствия
в
моменты
времени
kT,
kT
-
Т
и
kT
-
2Т.
Расчетный
алгоритм
регулятора
представлен
на
рис.
9.13.
Дискретизация
с
использованием
матричной
экспоненты.
Метод
обеспечивает
получение
точной
дискретной
модели
блоков,
на
вход
которых
поступает
кусочно
постоянное
воздействие.
Рассмотрим
объект
управления
(9.26)-(9.27)
цифровой
системы
с
кусочно
постоянным
управляющим
воздействием
u(t)
(см.
9.1.2
и
замечание
9.2).
Решение
уравнения
(9.26)
для
начального
значения
х(О)
=
хо
имеет
вид
x(t)
=
еА'хо
+
J.'
eA('-т)
Вu(т)
dr.
(9.37)
При
t =
kT
получим
x(k) = e
AkT
хо
+
J.kT
eA(kT-r)
Вu(т)
dr,
(9.38)
а
при
t = (k +
I)Т
-
r(k+l)T
x(k
+ 1) = e
A
(k+l)T
хо
+
Jo
e
A
«k+l)T-Т)
Вu(
-т)
dr
=
=
eATeAkT
хо
+
е
АТ
e
AkT
J.kT
е-
Ат
Вu(т)
dr +
/.
(k+l)T
+
e
A
«k+l)T-Т)
Вu(т)
dr.
kT
(9.39)

302
Глава
9.
Цифровые
системы
упраsrieни~
Подставляя
(9.38)
в
(9.39)
и
принимая
во
внимание
ПОС'I'оянство
u(t)
на
интервале
[kT, (k +
I)Т),
получим
peKyppeHTHO~.
выражение
/.
(k+l)T
x(k
+ 1) =
е
АТ
x(k) +
e
A
(k+l)T-т
Bdr
u(k).
kT
(9.40)
Окончательно,
з~пише~
дискретную'модель
ОУ
(9.26)-(9.27)
в
виде
разностного
уравнения
где
C
d
=
С,
x(k
+ 1)
y(k)
= Adx(k) + Bdu(k),
Cdx(k),
'Т
2
Tj
.
1 +
ТА
+
-,
А
2
+ ... +
1А)
+ ... ,
2.
).
Т
. . 2 .
1
А
''Т
Т
2
ТЗ.
B
d
=
е
т
В
dr
=
T~T+
,А
+
-,
А
+ ... +
("
1),А)
+
..
.
)В.
о
2.
3.
) + .
(9.41)
(9.42)
Обратим
внимание
на
отличие
выражений
для
вычисления
матриц
A
d
,
Bd
от
по
лученных
методом
Эйлера.
Нетрудно
видеть,
что
в
последнем
случае
для
расчета
матричной
экспоненты
использовалась
приближенная
формула
ехр(АТ)
~
1 +
Т
А,
чем
и
была
обусловлена
погреШI:IQСТЬ
указанного
метода.
Замечание
9.3.
Напомним,
что
для
автономной
модели
состояние-выход,
т.
е.
ли
нейноП
iистемы,
"~a
вход
~о+орой
не
'поступает
внешних
воздействий,
проблема
дис~рети~ации
~'чомощ~ю
.М~ТРИЧН9,Й
экспоненты
решается
с
абсолютной
точно-
стью
(см.
9.1.1). "
Замечание
9.4.
Обычно
кроме
входного
сигнала
и
на
объект
управления
оказывают
gлияни~
80эмущающие
воздействия,
которые
являются
'сигналами
непрерывного
времени.
При
дискре·тизации
возмущения
полагаются
кусочно-постоянными,
что
вызывает
появление
методических
ошибок
(см.
9.2.2).
Расширенная
дискретная
модель
ОУ
(учет
запаздывания).
Принимая
во
вни
мание,
что
входной
сигнал
u(kT)
является
запаздывающим
по
сравнению
с
иде
альным
сигналом
на
выходе
цифрового
регулятора
u'(kT)
(см.
9.1.3
и
пример
9.3),
введем
в
рассмотрение
дополнительный
динамический
элемент
-
звено чистоtо
запаздывания,
и
запишем
u«k
+
I)Т)
'=
u'(kT),
(9.43)
Определим
расширенный
вектор
состояния
I
x(k) I
xp(k) = u(k)
9.2.
Проблемы
дискретизации
непрерывных
моделей
и
сгруппируем
уравнения
(9.41)-(9.42)
и
(9.26):
где
xp(k +
1)
= Apxp(k) + Bpu'(k),
y(k) = Cpxp(k),
Ар
= I
~d ~"
I
,В
р
= I n
С
р
=
I
С"
О
1·
зоз
(9.44)
(9.45)
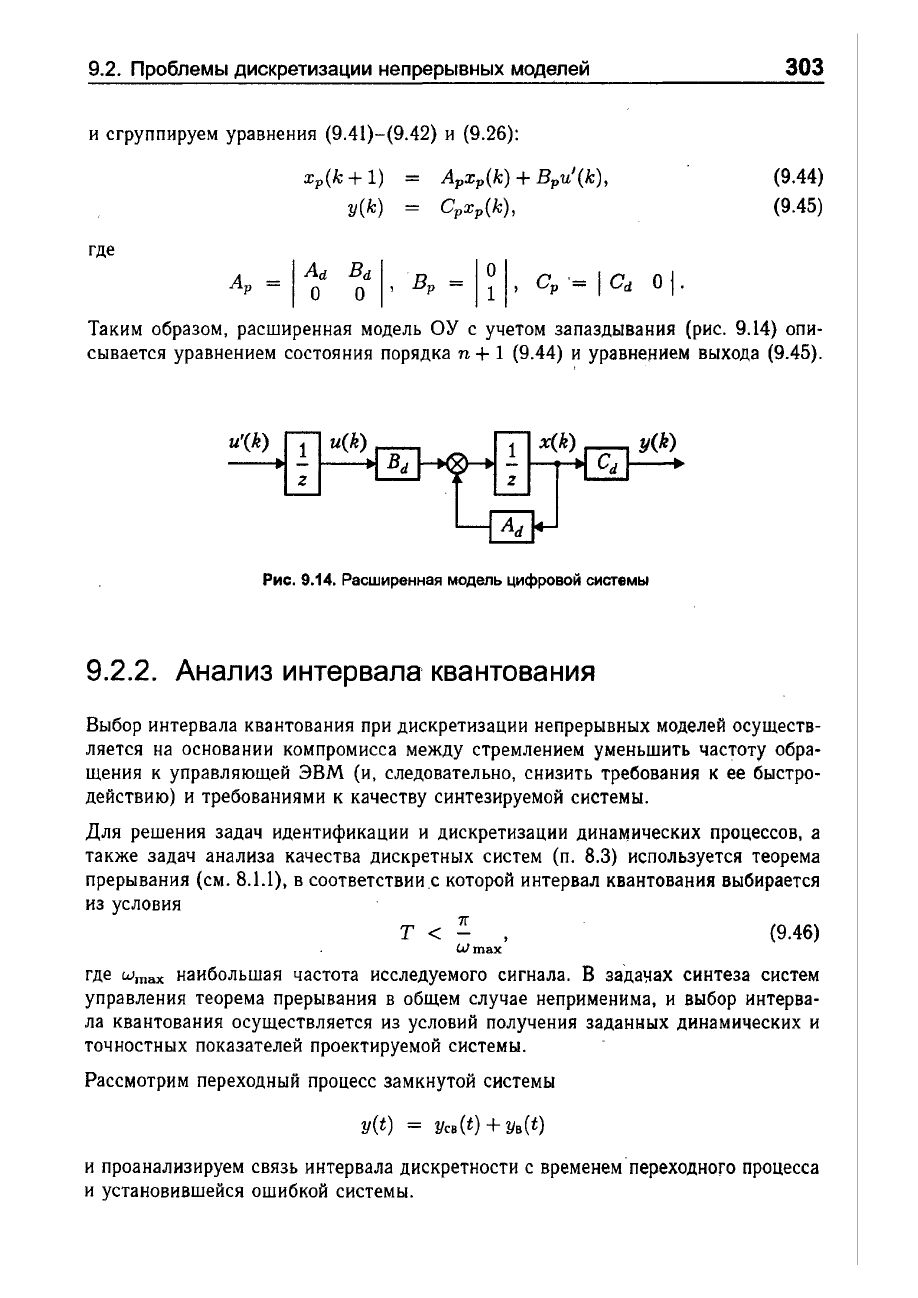
Таким
образом,
расширенная
модель
ОУ
с
учетом
запаздывания
(рис.
9.14)
опи
сывается
уравнением
состояния
порядка
n + 1 (9.44)
~
уравнением
выхода
(9.45).
Рис.
9.14.
Расширенная
модель
цифровой
системы
9.2.2.
Анализ
интервала'
квантования
Выбор
интервала
квантования
при
дискретизации
непрерывных
моделей
осуществ
ляется
на
основании
компромисса
между
стремлением
уменьшить
частоту
обра
щения
к
управляющей
ЭВМ
(и,
следовательно,
снизить
требования
к
ее
быстро
действию)
и
требованиями
к
качеству
синтезируемой
системы.
Для
решения
задач
идентификации
и
дискретизации
динамических
процессов,
а
также
задач
анализа
качества
дискретных
систем
(п.
8.3)
используется
теорема
прерывания
(см.
8.1.1),
в
соответствии.с
которой
интервал
квантования
выбирается
из
условия
1г
Т
< - ,
l.A)max
(9.46)
где
l.A)max
наибольшая
частота
исследуемого
сигнала.
В
задауах
синтеза
систем
управления
теорема
прерывания
в
общем
случае
неприменима,
и
выбор
интерва
ла
квантования
осуществляется
из
условий
получения
заданных
динамических
и
точностных
показателей
проектируемой
системы.
Рассмотрим
переходный
процесс
замкнутой
системы
y(t) = ycs(t) + ys(t)
и
проанализируем
связь
интервала
дискретности
с
временем
переходного
процесса
и
установившейся
ошибкой
системы.

Э04
Глава
9.
Цифровые
системы
управления
Напомним,
что
для
линейной
дискретной
системы
n-го
порядка
возможно
завер
шение
переходных
процессов
за
n
шагов
(см.
свойства
8.2-8.3,
подразделы
8.1.3-
8.2.1).
Следовательно,
в
общем
случае
время
затухания
t
n
свободной
составляющей
Уев
удовлетворяет
условию
t
n
~
nТ.
Из
последнего
неравенства
получаем
формулу
т
< t
n
- ,
(9.47)
n
которая
определяет
наибольшее
значение
интервала
квантования,
необходимое
для
получения
заданного
времени
переходного
процесса
t
n
•
Пример
9.4.
Рассмотрим
объект
управления
(9.16)
(пример
9.3)
и
его
дискретную
модель
y((k +
I)Т)
= y(kT) + KoTu(kT).
(9.48)
Стабилизация
объекта
осуществляется
пропорциональным
алгоритмом
управлен~я
u(kT) =
-Кру(kТ),
где
коэффициент
обратной
связи
К
р
выбирается
из
условия
получения
заданного
времени
переходного
процесса
t
n
замкнутой
системы
y((k +
I)Т)
=
(1
- KpKoT)y(kT).
(9.50)
Так
как система
имеет
первый
порядок,
то
интервал
дискретности
должен
удовле
творять
условИJO
т
~
t
n
.
После
выбора
Т
значение
полюса
замкнутой
системы
определяется
по
формуле
Zl
=
7]
=
е
3Т
/
tп
(см.
8.3.l),
а
значение
коэффициента
обратной
связи
-
1
-Zl
К
р
=
КоТ'
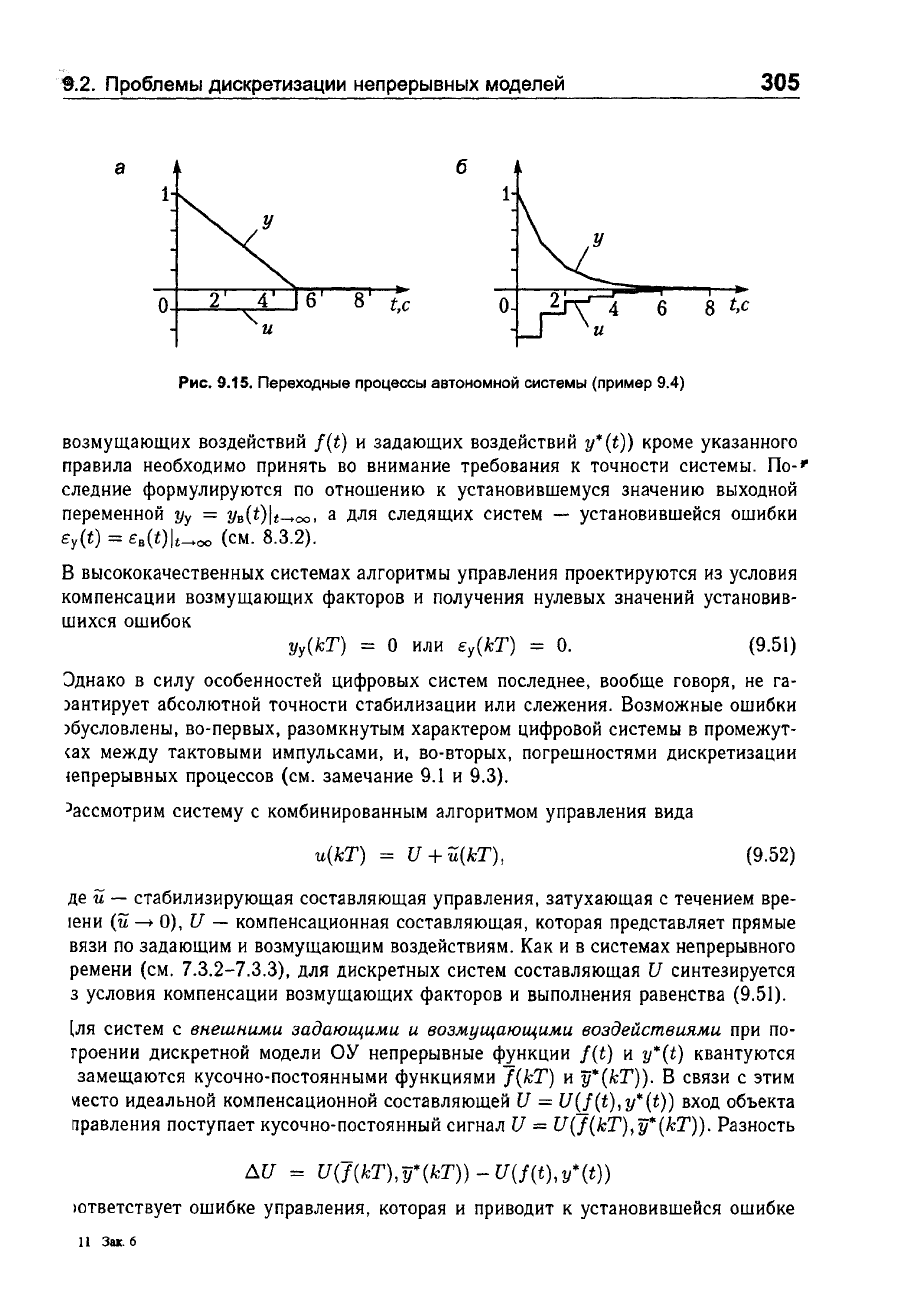
На
рис.
9.15
для
случая
t
п
= 5
с
представлены
графики
переходных
процессов
ОУ
(9.16) y(t)
и
u(t).
Рис.
9.15,
а
соответствует
предельно
допустимому
значению
т
=
t
п
= 5
с,
для
которого
получено
К
р
=
0.2,
а
рис.
9.15,
б
-
значению
Т
=
= 1
с
< t
n
,
для
которого
К
р
=
0.5.
О
Неравенство
(9.47)
используется
для
определения
интервала
квантования
автоном
ных
систем.
Для
нахождения
значения
Т
возмущенной
системы
(в
присутствии
~.2.
Проблемы
дискретизации
непрерывных
моделей
305
а
б
1
8
t,c
о
6
8
t,c
Рис.
9.15.
Переходные
процессы
автономной
системы
(пример
9.4)
возмущающих
воздействий
f(t)
и
задающих
воздействий
y*(t)
кроме
указанного
правила
необходимо
принять
во
внимание
требования
к
точности
системы.
По-"
следние
формулируются
по
отношению
к
установившемуся
значению
выходной
переменной
Уу
=
Yb(t)lt-+оо,
а
для
следящих
систем
-
установившейся
ошибки
€y(t) =
€B(t)lt-+oo
(см.
8.3.2).
В
высококачественных
системах
алгоритмы
управления
проектируются
из
условия
компенсации
возмущающих
факторов
и
получения
нулевых
значений
установив
шихся
ошибок
Yy(kT) =
О
или
€y(kT) =
о.
(9.51)
Jднако
в
силу
особенностей
цифровых
систем
последнее,
вообще
говоря,
не
га
)антирует
абсолютной
точности
стабилизации
или
слежения.
Возможные
ошибки
)бусловлены,
во-первых,
разомкнутым
характером
цифровой
системы
в
промежут
(ах
между
тактовыми
импульсами,
и,
во-вторых,
погрешностями
дискретизации
iепрерывных
процессов
(см.
замечание
9.1
и
9.3).
)ассмотрим
систему
с
комбинированным
алгоритмом
управления
вида
u(kT) = U + u(kT) ,
(9.52)
де
и
-
стабилизирующая
составляющая
управления,
затухающая
с
течением
вре
lени
(и
~
о),
U -
компенсационная
составляющая,
которая
представляет
прямые
вязи
по
задающим
и
возмущающим
воздействиям.
Как
и
в
системах
непрерывного
ремени
(см.
7.3.2-7.3.3),
для
дискретных
систем
составляющая
U
синтезируется
з
условия
компенсации
возмущающих
факторов
и
выполнения
равенства
(9.51).
[ля
систем
с
внешними
задающими
и
возмущающими
воздействиями
при
по
гроении
дискретной
модели
ОУ
непрерывные
функции
f(t)
и
y*(t)
квантуются
замещаются
кусочно-постоянными
функциями
](kT)
и
Y*(kT)).
В
связи
с
этим
\1есто
идеальной
компенсационной
составляющей
U =
U(f(t),
y*(t))
вход
объекта
rJравления
поступает
кусочно-постоянный
сигнал
U =
U(](kT),
y*(kT)).
Разность
6.и
=
U(](kT),
y*(kT)) -
U(f(t),
y*(t))
ютветствует
ошибке
управления,
которая
и
приводит
к
установившейся
ошибке
11
Зu.6

З06
Глава
9.
Цифровые
системы
управления
цифровой
системы.
Очевидно,
что
для
уменьшения
функции
дИ
требуется
со
кращение
интервала
квантования
Т,
причем
выполнения
условия
(9.46)
теоремы
прерывания
обычно
оказывается
недостаточно.
ПРU'м'ер
9.5.
Рассмотрим
возмущенный
объект
управления
y(t) =
Ко
(u(t) -
f(t)).
(9.53)
Дискретная
модель
объекта
при
допущении,
что
f(t)
~
j(kT),
принимает
вид
y((k
+
l)Т)
=
y(kT)
+
KoT(u(kT)
-
f(kT)),
(9.54)
а
комбинированный
алгоритмом
управления
-
u(kT)
=
и
- Kpy(kT).
(9.55)
Здесь
компенсационная
составляющая
выбирается
как
и
=
f(kT)
(9.56)
и
обеспечивает
получение
в
дискретные
моменты
времени
kT
нулевой
установив
шейся
ошибки
замкнутой
дискретной
системы
(9.54)-(9.55),
т.
е.
выполняется:
y(kT) --+
О
при
k --+
00.
Тем
не
менее
в
силу
различия
реального
возмущения
f(t)
и
поступающей
на
объект
управления
кусочно-постоянной
функции
j(kT)
возникает
ошибка
управления
дИ
=
j(kT)
-
f(t),
(9.57)
что
обусловливает
погрешность
стабилизации
возмущенной
системы.
а
б
1
1
о
t,c
о
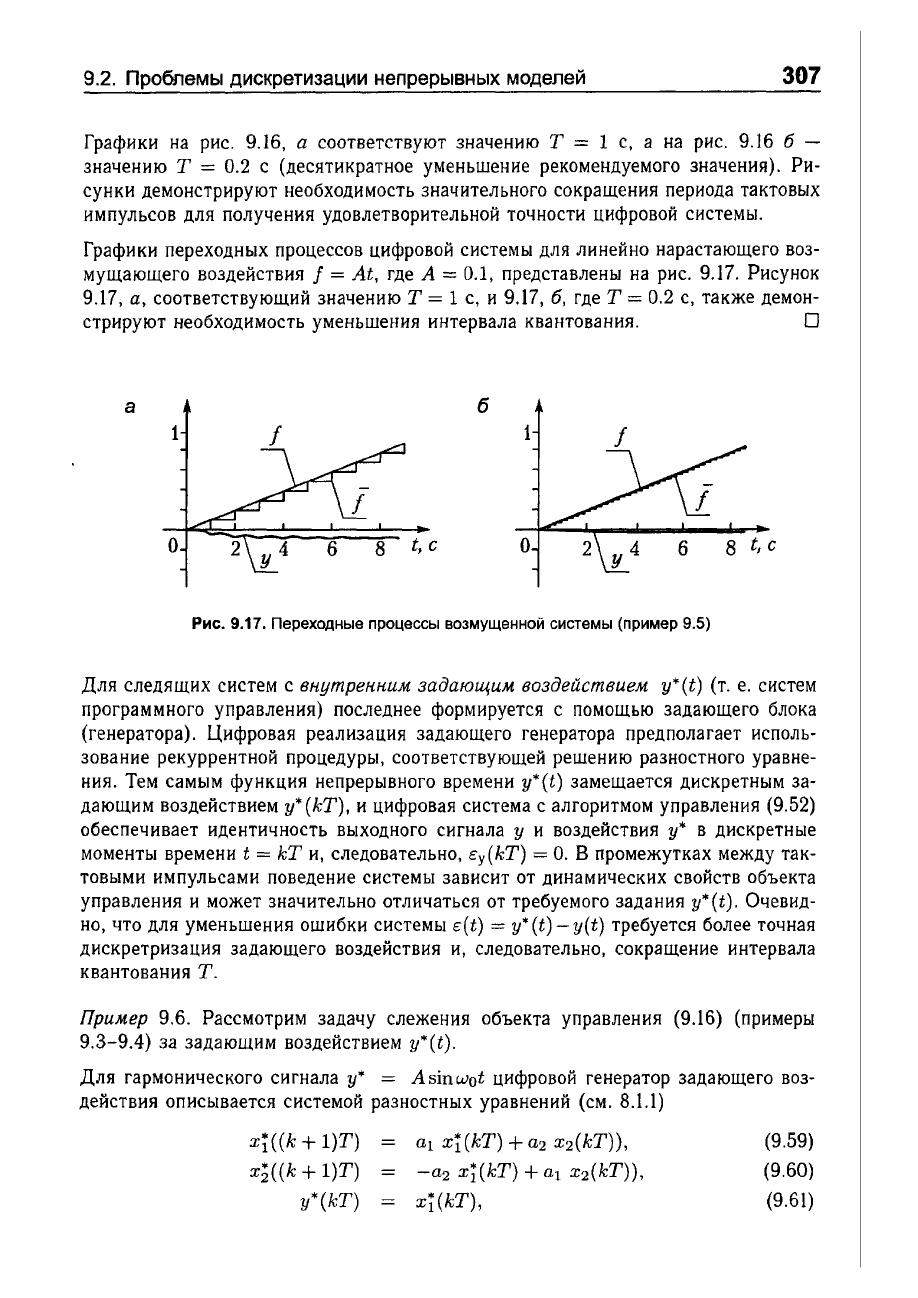
Рис.
9.16.
Переходные
процессы
возмущенной
системы
(пример
9.5)
Для
гармонического
возмущающего
воздействия
f =
А
sin
VJot,
где
А
= 0.4,
VJo
=
=
1г
/2,
на
рис.
9.16
представлены
графики
переходных
процессов
рассматриваемой
цифровой
системы
- y(t),
j(kT)
и
f(t).
Здесь
условие
теоремы
прерывания
(9.46)
принимает
вид
т
< 2
с.
(9.58)
9.2.
Проблемы
дискретизации
непрерывных
моделей
307
Графики
на
рис.
9.16,
а
соответствуют
значению
Т
= 1
с,
а
на
рис.
9.16 6 -
значению
Т
=
0.2
с
(десятикратное
уменьшение
рекомендуемого
значения).
Ри
сунки
демонстрируют
необходимость
значительного
сокращения
периода
тактовых
импульсов
для
получения
удовлетворительной
точности
цифровой
системы.
Графики
переходных
процессов
цифровой
системы
для
линейно
нарастающего
воз
мущающего
воздействия
f = At,
где
А
=
0.1,
представлены
на
рис.
9.17.
Рисунок
9.17,
а,
соответствующий
значению
Т
= 1
с,
и
9.17,
6,
где
Т
=
0.2
с,
также
демон
стрируют
необходимость
уменьшения
интервала
квантования.
О
а
б
1
1
о
t,
с
о
Рис.
9.17.
Переходные
процессы
возмущенной
системы
(пример
9.5)
Для
следящих
систем
с
внутренним
задающим
воздействием
y*(t)
(т.
е.
систем
программного
управления)
последнее
формируется
с
помощью
задающего
блока
(генератора).
Цифровая
реализация
задающего
генератора
предполагает
исполь
зование
рекуррентной
процедуры,
соответствующей
решению
разностного
уравне
ния.
Тем
самым
функция
непрерывного
времени
y*(t)
замещается
дискретным
за
дающим
воздействием
y*(kT),
и
цифровая
система
с
алгоритмом
управления
(9.52)
обеспечивает
идентичность
выходного
сигнала
у
и
воздействия
у*
в
дискретные
моменты
времени
t =
kT
и,
следовательно,
€y(kT) =
О.
в
промежутках
между
так
товыми
импульсами
поведение
системы
зависит
от
динамических
свойств
объекта
управления
и
может
значительно
отличаться
от
требуемого
задания
y*(t).
Очевид
но,
что
для
уменьшения
ошибки
системы
€(t) =
y*(t)
-y(t)
требуется
более
точная
дискретризация
задающего
воздействия
и,
следовательно,
сокращение
интервала
квантования
Т.
Пример
9.6.
Рассмотрим
задачу
слежения
объекта
управления
(9.16)
(примеры
9.3-9.4)
за
задающим
воздействием
y*(t).
Для
гармонического
сигнала
у*
=
А
sin
l.JJot
цифровой
генератор
задающего
воз
действия
описывается
системой
разностных
уравнений
(см.
8.1.1)
xi(k
+
l)Т)
x;(k
+
l)Т)
y*(kT)
аl
xi(kT)
+
а2
x2(kT)),
=
-а2
xHkT)
+
аl
x2(kT)),
=
xHkT),
(9.59)
(9.60)
(9.61)
308
Глава
9.
'Цифровые
системы
управления
где
аl
=
COSUJoT,
а2
=
sinUJoT,
хНО)
=
О,
Х2(0)
=
А.
Введем
в
рассмотрение
ошибку
слежения
€ =
у*
-
у
=
x~
-
у
и
с
использованием
уравнений
(9.48)
и
(9.59)-(9.60)
найдем
€((k +
l)Т)
= g(kT) +
(аl
-
l)x~(kT)
+
a2x2(kT»
- KoTu(kT).
(9.62)
Алгоритм
комбинированного
управления,
обеспечивающий
получение
затухающей
свободной
составляющей
и
нулевой
установившейся
ошибки,
принимает
вид
(9.63)
Алгоритм
обеспечивает
абсолютную
точность
воспроизведения
дискретного
сиг
нала
y*(kT),
однако
не
гарантирует
получения
нулевого
значения
ошибки
€(t) =
=
y*(t) - y(t)
в
промежутках
между
тактовыми
импульсами.
а
б
1
о
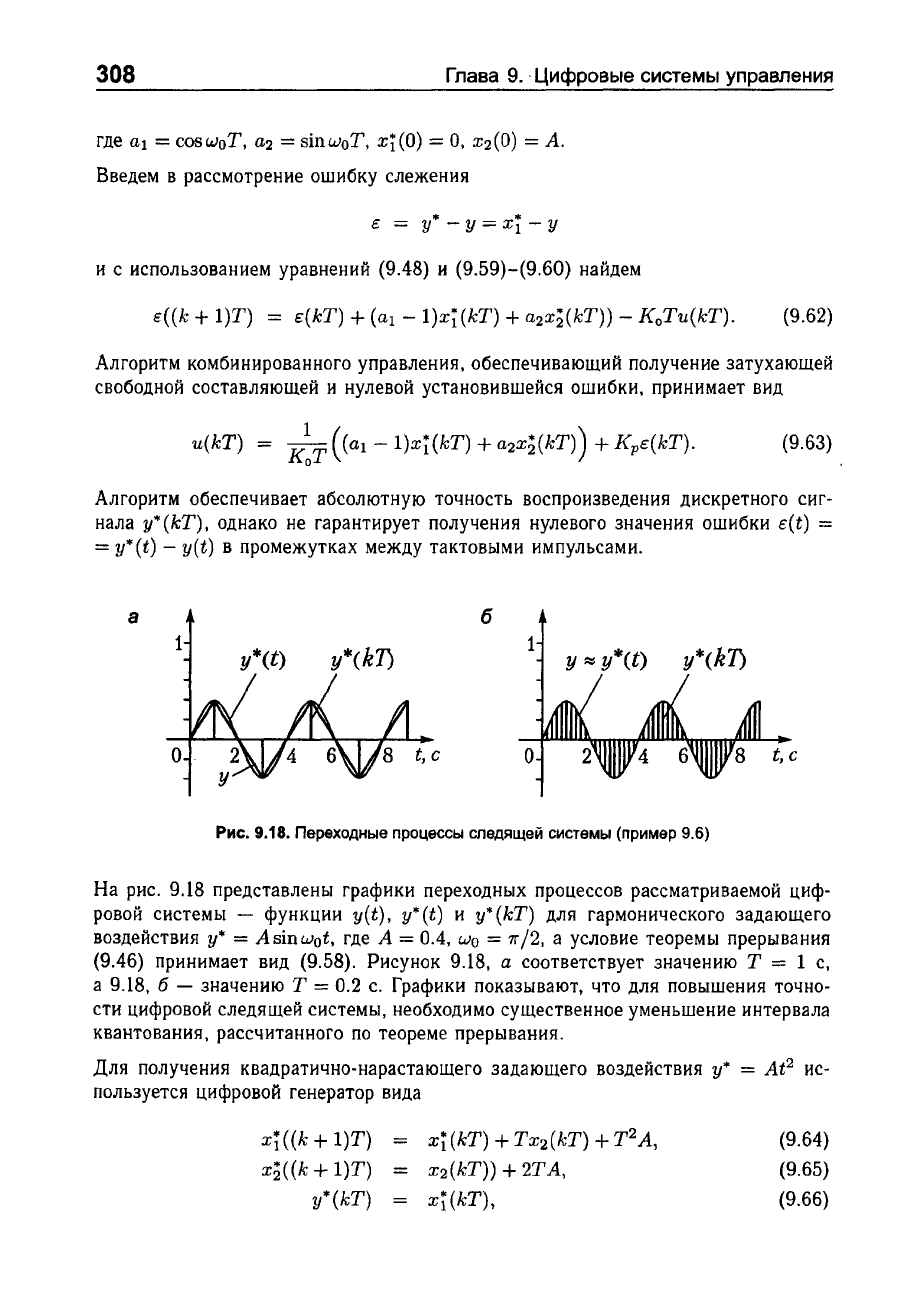
Рис.
9.18.
Переходные
процессы
следящей
системы
(пример
9.6)
На
рис.
9.18
представлены
графики
переходных
процессов
рассматриваемой
циф
ровой
системы
-
функции
y(t), y*(t)
и
y*(kT)
для
гармонического
задающего
воздействия
у*
= AsinUJot,
где
А
= 0.4,
UJo
=
7r/2,
а
условие
теоремы
прерывания
(9.46)
принимает
вид
(9.58).
Рисунок
9.18,
а соответствует
значению
Т
= 1
с,
а
9.18,
б
-
значению
Т
=
0.2
с.
Графики
показывают,
что
для
повышения
точно
сти
цифровой
следящей
системы,
необходимо
существенное
уменьшение
интервала
квантования,
рассчитанного
по
теореме прерывания.
Для
получения
квадратично-нарастающего
задающего
воздействия
у*
=
At
2
ис
пользуется
цифровой
генератор
вида
xi((k
+
l)Т)
x2((k +
l)Т)
y*(kT)
=
x~(kT)
+ TX2(kT) +
т
2
А,
= x2(kT» +
2ТА,
xi(kT),
(9.64)
(9.65)
(9.66)
9.2.
Проблемы
дискретизации
непрерывных
моделей
309
где
хНО)
=
Х2(О)
=
О.
Из
уравнений
(9.48)
и
(9.59)-(9.60)
найдем
модель
ошибки
слежения
e«k
+
l)Т)
=
e(kT)
+
Tx;(kT)
+
т
2
А
-
TKou(kT),
(9.67)
а
затем
-
алгоритм
комбинированного
управления
u(kT)
=
(9.68)
обеспечиващий
абсолютную
точность
воспроизведения
дискретного
сигнала
y*(kT).
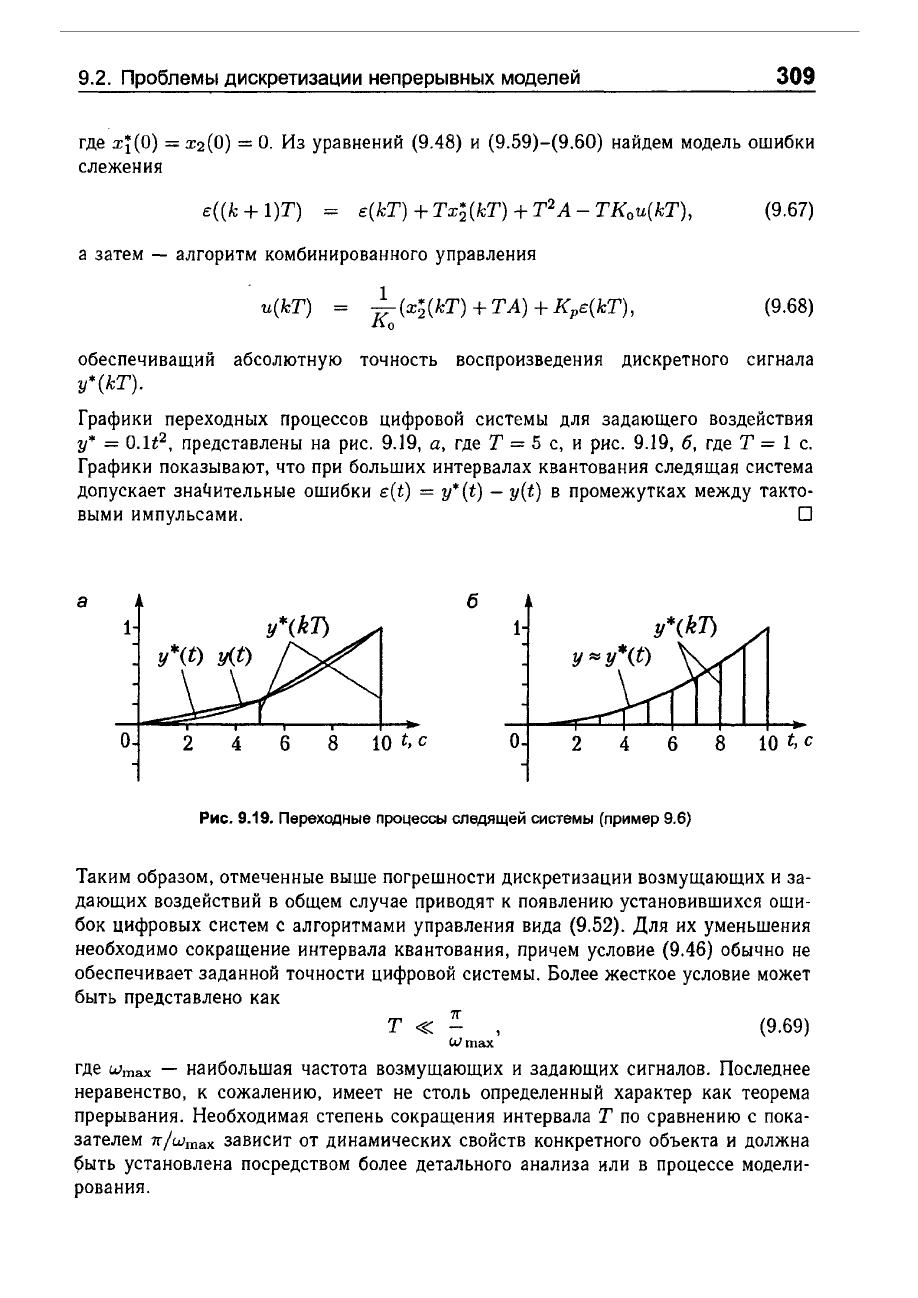
Графики
переходных
процессов
цифровой
системы
для
задающего
воздействия
у*
= O.lt
2
,
представлены
на
рис.
9.19,
а,
где
Т
= 5
с,
и
рис.
9.19,
б,
где
Т
= 1
с.
Графики
показывают,
что
при
больших
интервалах
квантования
следящая
система
допускает
значительные
ошибки
e(t) = y*(t) - y(t)
в
промежутках
между
такто
выми
импульсами.
О
а
б
1
1
о
2 4
6
8
10
t,
с
о
2 4 6
8
10
t,
с
Рис.
9.19.
Переходные
процессы
следящей
системы
(пример
9.6)
Таким
образом,
отмеченные
выше
погрешности
дискретизации
возмущающих
и
за
дающих
воздействий
в
общем
случае
приводят
к
появлению
установившихся
оши
бок
цифровых
систем
с
алгоритмами
управления
вида
(9.52).
Для
их
уменьшения
необходимо
сокращение
интервала
квантования,
причем
условие
(9.46)
обычно
не
обеспечивает
заданной
точности
цифровой
системы.
Более
жесткое
условие
может
быть
представлено
как
1г
Т
«-
,
l.A.Jшах
(9.69)
где
l.A.J
шах
-
наибольшая
частота
возмущающих
и
задающих
сигналов.
Последнее
неравенство,
к
сожалению,
имеет
не
столь
определенный
характер
как
теорема
прерывания.
Необходимая
степень
сокращения
интервала
Т
по
сравнению
с
пока
зателем
1Г/l.A.J
шах
зависит
от
динамических
свойств
конкретного
объекта
и
должна
~ЫTЬ
установлена
посредством
более детального
анализа
или
в
процессе
модели
рования.
