Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.


210
Глава
7.
Методы
управления'
и
синтез
еДУ
I
I
I
--------------
у
Рис.
7.10.
Система
управления
состоянием
задающий
блок
ЭБ
(генератор
задающего
воздействия):
±*
А*х*,
у*
=
С*х*;
модель
внешней
среды
ВС
(генератор
возмущающего
воздействия):
~
Г~,
f =
H~
(7.26)
(7.27)
(7.28)
(7.29)
и
регулятор
состояния
(алгоритм
управления)
Р.
В
тех
случаях,
когда
не
все
переменные
состояния
объекта
управлеЩIЯ
(и/или
ВС)
измеряемы,
структура
си
стемы
управления
должна
быть
дополнена
устройством
(алгоритмом)
оценивания
состояния,
или
н,аблюдателем,
который
и
осуществляет
расчет
неизмеряемых
пе
ременных
(см.
1.5.3
и
п.
7.4).
Более
того,
В,ряде
случаев
появляется
необходимость
опр~деления
(оценивания.)
неизвестных
пара
метров
ОУ
или
внешней
среды
и,
сле
довательно,
построения
идентификаторов
параметров
(см.
1.5.3
и
[32,
47]).
Синтезом
называется
процедура
построения
системы,
т.
е.
выбора
алгоритмов
упраВ.1Iения
и
оценивания
(переменных
и
пара
метров)
по
заданным
динамическим
и
точностным
показателям
качества.
В
этом
'разделе
рассматриваются
временные
процедуры
синтеза,
основанные
на
методе
пространства
состояний
и
позволяющие
осуществить
построение
систе
мы
аналитическим
путем.
Типовая
процедура
синтеза
САУ
включает
следующие
этапы:
•
решение
задачи
стабилизации
невозмущенного
ОУ;
•
решение
задачи
стабилизации
в
условиях
действия
возмущений;
•
синтез
следящей
системы;
•
синтез
наблюдателя.
Более
подробный
анализ
методов
и
систем
управления
состоянием
приведен
в
работах
[2,
3,
6,
10,
14, 19,
20,
34,
40].
7:~З~)
I?~ГYll~TOPЫ
И
,СИСТ~~ql
управления:состоянием
211
7.3.1.
Синтез
алгоритма
стабилизации
и
метод
модального
управления
х
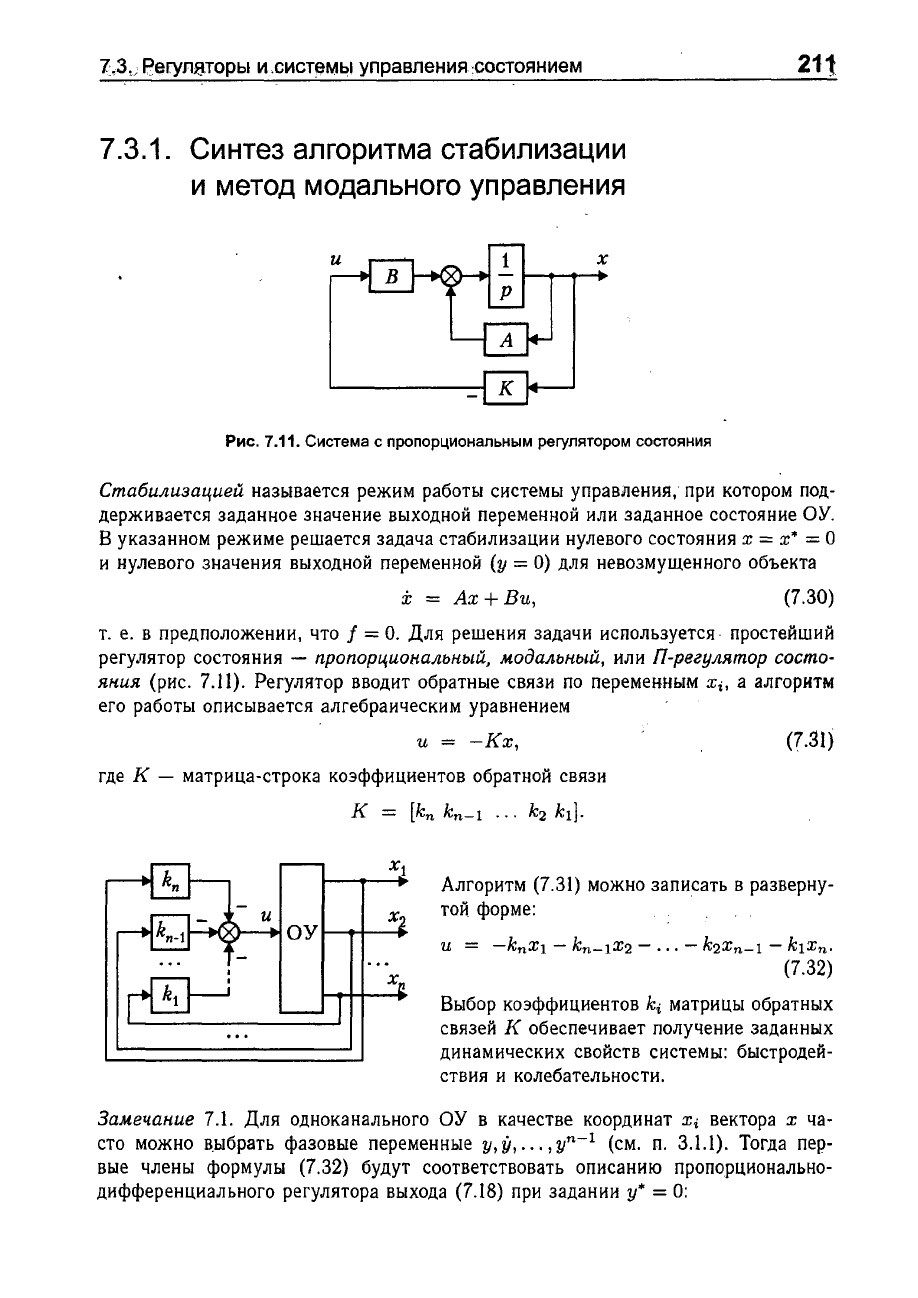
Рис.
7.11.
Система
с
пропорциональным
регулятором
состояния
Стабилизацией
называется
режим
работы
системы
управления;
при
котором
под
держивается
заданное
значение
выходной
переменной
или
заданное
состояние
ОУ.
В
указанном
режиме
решается
задача
стабилизации
нулевого
состояния
Х
=
х*
=
О
и
нулевого
значения
выходной
переменной
(у
=
О)
для
невозмущенного
объекта
х
=
Ах+Вu,
(7.30)
т.
е.
в
предположении,
что
f =
О.
ДЛЯ
решения
задачи
используется·
простейший
регулятор
состояния
-
nроnорциональный,
модальный,
или
П-регулятор
состо
яния
(рис.
7.11).
Регулятор
вводит
обратные
связи
по
переменным
Xi,
а
алгоритм
его
работы
описывается
алгебраическим
уравнением
и
=
-Кх,
(7.31)
где
К
-
матрица-строка
коэффициентов
обратной
связи
К
=
[k
n
k
n
-
1
••.
k
2
k
1
}.
и
х
~ИХ)--~
ОУ
1--"-+--+
Алгоритм
(7.31)
можно
записать
в
разверну
той
форме:
и
=
-knХl
-
kn-1X2
-
...
- k
2
x
n
-l
-
k1x
n
.
(7.32)
Выбор
коэффициентов
k
i
матрицы
обратных
связей
К
обеспечивает
получение
заданных
динамических
свойств
системы:
быстродей
ствия
и
колебательности.
Замечание
7.1.
Для
одноканального
ОУ
в
качестве
координат
Xi
вектора
х
ча
сто
можно
в.ыбрать
фазовые
переменные
у,
у,
... ,
yn-l
(см.
П.
3.1.1).
Тогда
пер
вые
члены
формулы
(7.32)
будут
соответствовать
описанию
пропорционально
дифференциального
регулятора
выхода
(7.18)
при
задании
у*
=
О:

212
Глава
7.
Методы
управления
и
синтезСДУ
u =
-k
у
- k
lY'
- - k .y
n
-
j
n
n-
.,.
J
•.•.
(7.33)
Поэтому
регуляторы
состояния
являются
обобщением
ПД-регуляторов,
хотя
и
не
содержат
в
явном
виде
дифференцирующих
звеньев.
После
подстановки
алгоритма
(7.31)
в
уравнение
объекта
(7.30)
получаем
уравне
ние
замкнутой
системы
(7.34)
где
Ас
=
А
-
ВК
-
матрица
замкнутой
системы,
определяющая
динамические
свойства
системы
с
пропорциональным
регулятором
состояния.
Соответствующий
характеристич.ескиЙ
полином
принимает
вид
ас(р)
=
det(pI
-
Ас)
=
рn
+
aclpn-l
+ ... +
a
cn
-lР
+
а
сn
.
в
соответствии
с
м-етодом-
м-одалыюго
управления
[2,
3,
10,
20]
устойчивость
по
ложения
равновесия
синтезируемой
системы
и
заданные
динамические
показатели
ее
качества
достигаются
за
счет
назначения
корней
Pci
=
Лi{А
с
}
характеристиче
ского
уравнения
ас(р)
=
О,
что,
в
свою
очередь,
обеспечивается
соответствующим
выбором
коэффициентов
обратных
связей
k
i
.
Метод
основывается
на
следующем
положении.
Свойство
7.1.
Если
система
(7.30), (7.25)
полностью
управляема,
то
существует
единственная
матрица
обратной
связи
К,
обеспечивающая
получение
заданных
значениА
корней
характеристи'ческого
полинома
замкнутой
системы
Pci
=
Лi{А
с
}.
Отметим,
что
в
рассматриваемом
случае
(при
отсутствии
возмущений)
регулятор
(7.31)
обеспечивает
абсолютную
точность
стабилизации
системы
в
заданной
точке
х*
=
О.
Прим-ер
7.8.
Для
типового
объекта
второго
порядка
(см.
пример
3.1)
модель
ВСВ
записывается
в
виде
где
Xl
=
Х2,
Х2
=
-а2Хl
-
alX2
+
Ьи,
У
=
Xl,
или
в
векторно-матричной
форме
(7.30),
где
Х =
I
~~
I = I
~
1,
А
-1-~2
(7.35)
(7.36)
(7.37)
7.3.
Регуляторы
и
системы
управления
состоянием
21
3
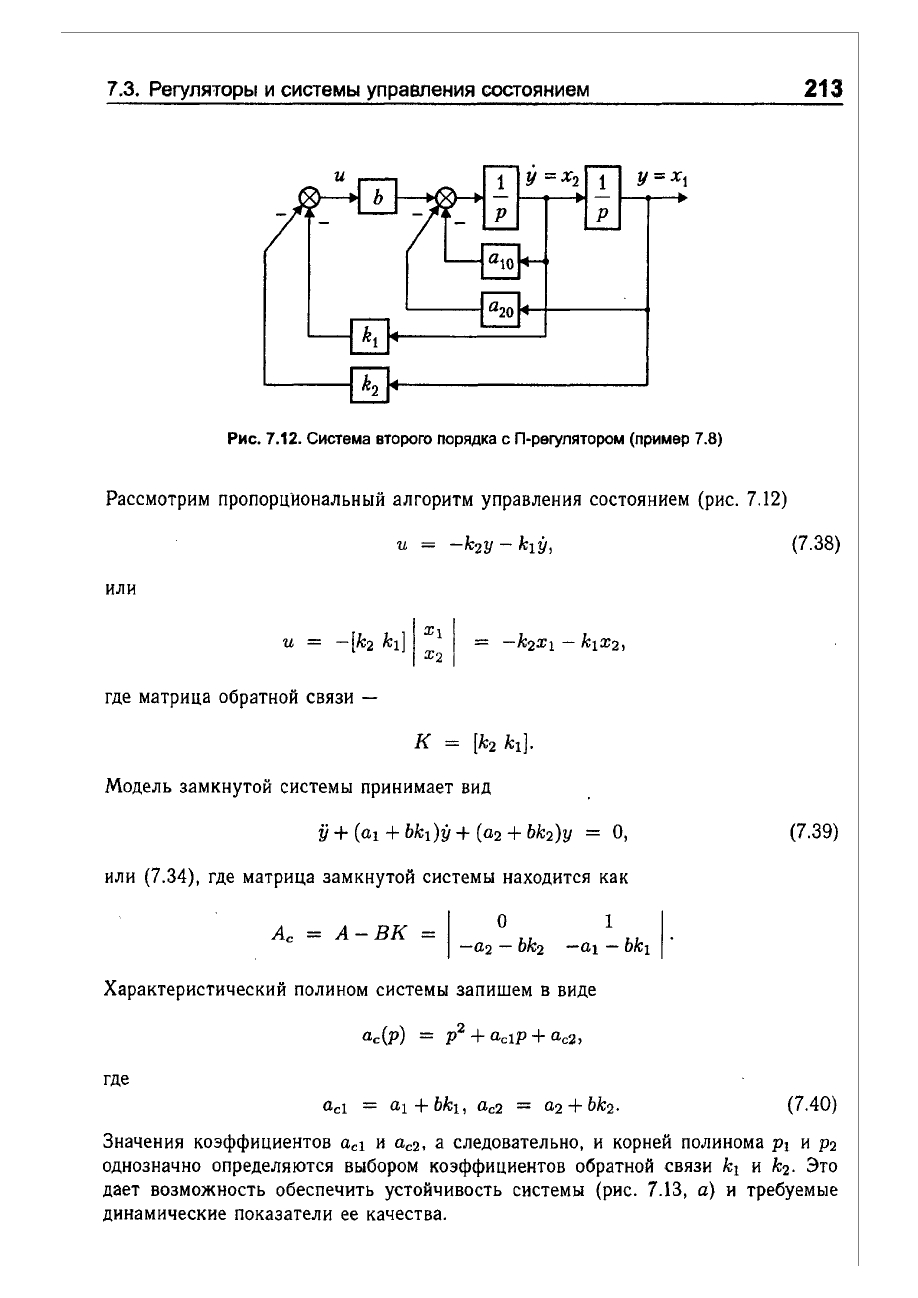
Рис.
7.12.
Система
второго
порядка
сП-регулятором
(пример
7.8)
Рассмотрим
пропорциональный
алгоритм
управления
состоянием
(рис.
7.12)
(7.38)
или
где
матрица
обратной
связи
-
Модель
замкнутой
системы
принимает
вид
(7.39)
или
(7.34),
где
матрица
замкнутой
системы
находится
как
Ас
=
А
-
ВК
= I
о
bk 1 bk
1·
-а2
- 2
-аl
- 1
Характеристический
полином
системы
запишем
в
виде
где
(7.40)
Значения
коэффициентов
а
с
l
и
а
с
2.
а
следовательно,
и
корней
полинома
Рl
и
Р2
однозначно
определяются
выбором
коэффициентов
обратной
связи
k
1
и
k
2
.
Это
дает
возможность
обеспечить устойчивость
системы
(рис.
7.13,
а)
и
требуемые
динамические
показатели
ее
качества.
214
Глава
7.
Методы
упра8ления
и
'синтез;
еду
а
б
о
t
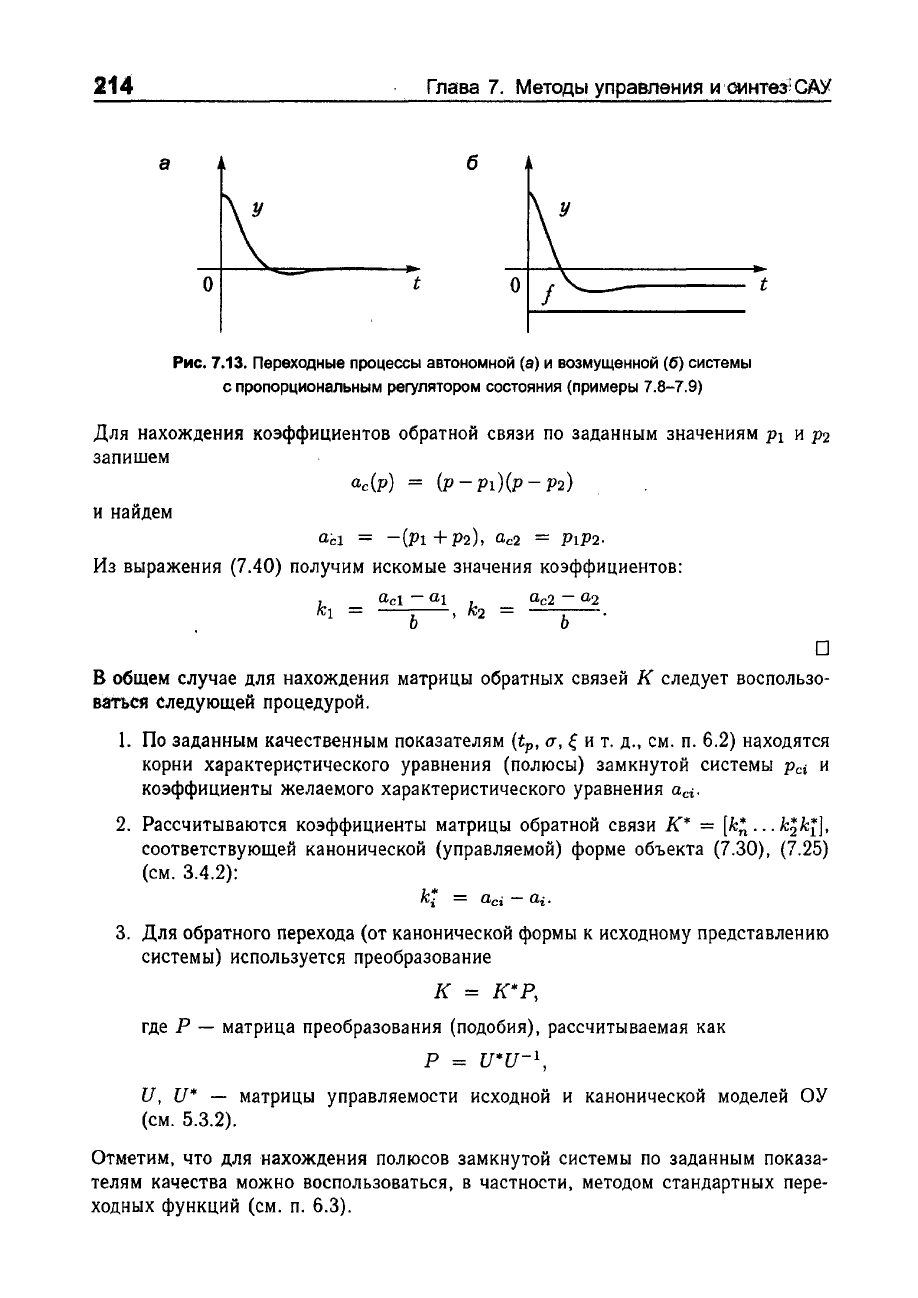
Рис.
7.13.
Переходные
процессы
автономной
(8)
и
возмущенной
(б)
системы
с
пропорциональным
регулятором
состояния
(примеры
7.8-7.9)
t
Для
нахождения
коэффициентов
обратной
связи
по
заданным
значениям
Р1 и
Р2
запишем
).f
найдем
а
с
1
=
-(Р1
+
Р2),
а
с
2
=
Р1Р2·
Из
выражения
(7.40)
получим
искомые
значения
коэффициентов:
а
с
1
-
а1
k _
а
с
2
-
а2
k
1
=
Ь
,2
-
Ь
о
в
общем
случае
для
нахождения
матрицы
обратных
связей
К
следует
воспользо
ваться
следующей
процедуроЙ.
1.
По
заданным
качественным
показателям
(t
p
,
(7,
~
и
т.
д.,
см.
п.
6.2)
находятся
корни
характеристического
уравнения
(полюсы)
замкнутой
системы
Pci
И
коэффициенты
желаемого
характеристического
уравнения
aci.
2.
Рассчитываются
коэффициенты
матрицы
обратной
связи
К*
=
[k~
...
k
2
ki),
соответствующей
канонической
(управляемой)
форме
объекта
(7.30), (7.25)
(см.
3.4.2):
3.
Для
обратного
перехода
(от
канонической
формы
к
исходному
представлению
системы)
используется
преобразование
К
=
К*Р,
где
Р
-
матрица
преобразования
(подобия),
рассчитываемая
как
Р
= u*u-
1
,
И,
U* -
матрицы
управляемости
исходной
и
канонической
моделей
ОУ
(см.
5.3.2).
Отметим,
что
для
нахождения
полюсов
замкнутой
системы
по
заданным
показа
телям
качества
можно
воспользоваться,
в
частности,
методом
стандартных
пере
ходных
функций
(см.
п.
6.3).

7:.3.',;
l?eryJilR-ТОРbl
и;системы
управления
'состоянием
215.
7.3.2.
Стабилизация
возмущенного
объекта
Рассмотрим
задачу
стабилизации
возмущенного
ОУ
вида
(7.24)-(7.25),
полагая,
что
возмущающее
воздействие
f(t)
является
выходом
модели
(7.28)-(7.29),
где
~
=
{~i}
-
nгмерный
вектор
состояния
внешней
среды.
В
условиях
действия
внешних
возмущений
точностные
показатели
системы
с
пропорциональным
регу
лятором
состояния
ограничены.
Повышение
установившейся
точности
может
быть
достигнуто
за
счет
увеличения
коэффициентов
обратных
связей,
использования
ПИ-регуляторов
или
регушtторов
комбинированного
типа.
Определим
точность
си
стемы
с
полученным
ранее
пропорциональным
регулятором,
а
далее
синтезируем
комбинированный
регулятор,
гарантирующий
получение
абсолютной
точности
воз
мущенной
системы.
Анализ
точности
системы
с
пропорциональным
и
ПИ-регулятором.
Уравне
ние
з~мкнутой
системы
с
пропорциональным
регулятором
получается
подстановкой
выражения
(7.31)
в
(7.24)
и
принимает
вид
х
=
Асх+
Df.
(7.41)
Выбор
матрицы
обратной
связи
К,
осуществленный
в
п.
7.3.1,
обеспечивает
.задан
ные
динамические
показатели
системы
(7.41).
Для
оценки
ее
точности
необходимо
проанализировать
поведение
системы
в
установившемся
режиме.
Наиболее
просто
определяются
точностные
показатели
стат'и~еского
режима,
т.
е.
для
постоянных
или
медленно
изменяющихся
возмущений
f
~
const.
Так
как
замкнутая
система
устойчива
и,'
следовательно,
det
A~
"::/
о;
то
из'
условия
х
=
о
находим
значения
установившихся
ошибок
(см.
3.2.3)
,
(7.42)
и
.
(7.43)
Выражения
показывают,
что
пропорциональный
регулятор
не
обеспечивает
абсо
лютной
точности
решения
рассматриваемой
задачи
(см.
рис.
7.13,
б),
Тем
не
менее
увеличение
коэффициентов
обратной
связи
k
i
(параметров
матрицы
К)
позволяет
уменьшить
значения
Х
у
и
Уу.
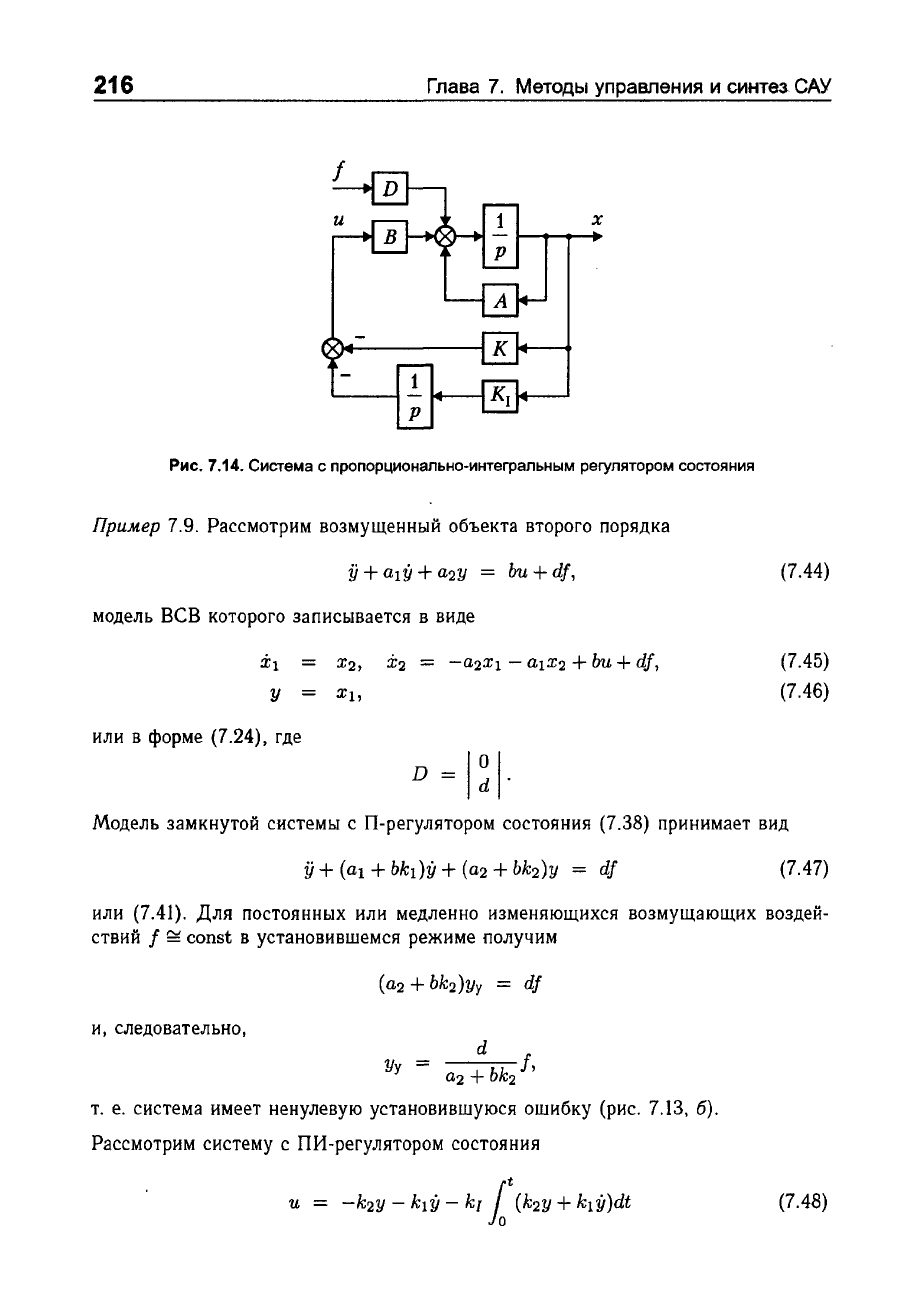
Повышение
точности
стабилизации
достигается
также
при
введении
в
состав
системы
контуров
интегральных
обратных
связей,
т.
е.
при
использовании
пропорционально-интегрального
(астатического)
регулятора
состояния
(рис.
7.14):
1
и
=
-Кх
-
-(K1x),
Р
где
К[
-
матрица
коэффициентов
обратной
связи
по
интегралу
от
вектора
со
стояния.
Интегральная
составляющая
указанного
алгоритма
с
течением
времени
обеспечивает
частичную
или
полную
компенсацию
возмущения
f(t).
216
Глава
7.
Методы
управления
и
синте:!
еду
х
Рис.
7.14.
Система
с
пропорционально-интегральным
реryлятором
состояния
Прuм.ер
7.9.
Рассмотрим
возмущенный
объекта
второго
порядка
модель
ВСВ
которого
записывается
в
виде
Хl
=
Х2,
Х2
=
-а2
Х
l
-
аl
Х
2
+
ьu
+ dj,
У
=
Хl,
или
в
форме
(7.24),
где
D = I
~I·
(7.44)
(7.45)
(7.46)
Модель
замкнутой
системы
с
П-регулятором
состояния
(7.38)
принимает
вид
(7.4
7)
или
(7.41).
Для
постоянных
или
медленно
изменяющихся
возмущающих
воздей
ствий
f
~
const
в
установившемся
режиме
получим
и,
следовательно,
d j
Уу
=
а2
+ bk
2
'
т.
е.
система
имеет
ненулевую
установившуюся
ошибку
(рис.
7.13,
б).
Рассмотрим
систему
с
ПИ-регулятором
состояния
(7.48)
7.3.
Регуляторы
и
системы
управления
состоянием
211
или
(7.49)
где
k]
-
постоянный
коэффициент.
Модель
замкнутой
системы
принимает
вид
(7.50)
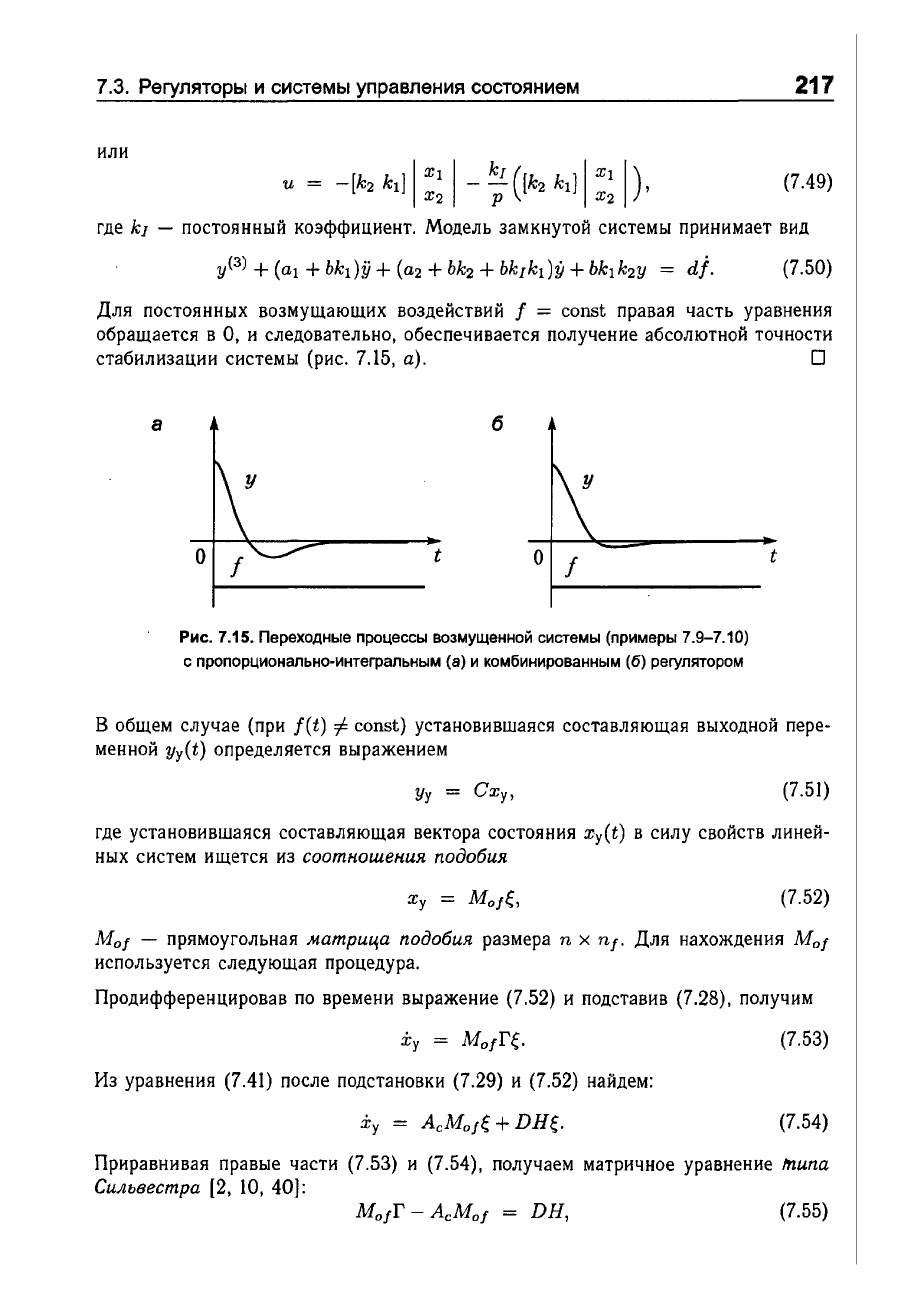
Для
постоянных
возмущающих
воздействий
f = const
правая
часть
уравнения
обращается
в
О,
и
следовательно,
обеспечивается
получение
абсолютной
точности
стабилизации
системы
(рис.
7.15,
а).
О
а
б
о
t
о
f
Рис.
7.15.
Переходные
процессы
возмущенной
системы
(примеры
7.9-7.10)
с
пропорционально-интегральным
(а)
и
комбинированным
(6)
реryлятором
t
в
общем
случае
(при
f(t)
i=
const)
установившаяся
составляющая
выходной
пере
менной
Yy(t)
определяется
выражением
(7.51)
где
установившаяся
составляющая
вектора
состояния
Xy(t)
в
силу
свойств
линей
ных
систем
ищется
из
соотношения
подобия
(7.52)
м
о!
-
прямоугольная
матрица
подобия
размера
n
Х
nf.
Для
нахождения
мо!
используется
следующая
процедура.
Продифференцировав
по
времени
выражение
(7.52)
и
подставив
(7.28),
получим
Х
у
=
Mofr~,
(7.53)
Из
уравнения
(7.41)
после
подстановки
(7.29)
и
(7.52)
найдем:
Х
у
=
AcMof~
+
DH~.
(7.54)
Приравнивая
правые
части
(7.53)
и
(7.54),
получаем
матричное
уравнение
muna
Сильвестра
[2,
10,
40]:
(7.55)
218
Гл"ава
7.
Методы
управления
и
синтеЗ;САУ
решением
которого
и
является
искомая
матрица
M
of
.
Таким
образом,
для
оцен
ки
точности
возмущенной
системы
с
пропорциональным
регулятором
необходимо
выполнить
следующие
действия.
1.
Решить
уравнение
(7.55)
и
найти
матрицу
M
of
.
2.
Рассчитать
вектор
Х
у
по
формуле
(7.52)
и
найти
установившуюся
ошибку
Yy(t) = CXy(t) =
CMOf~(t).
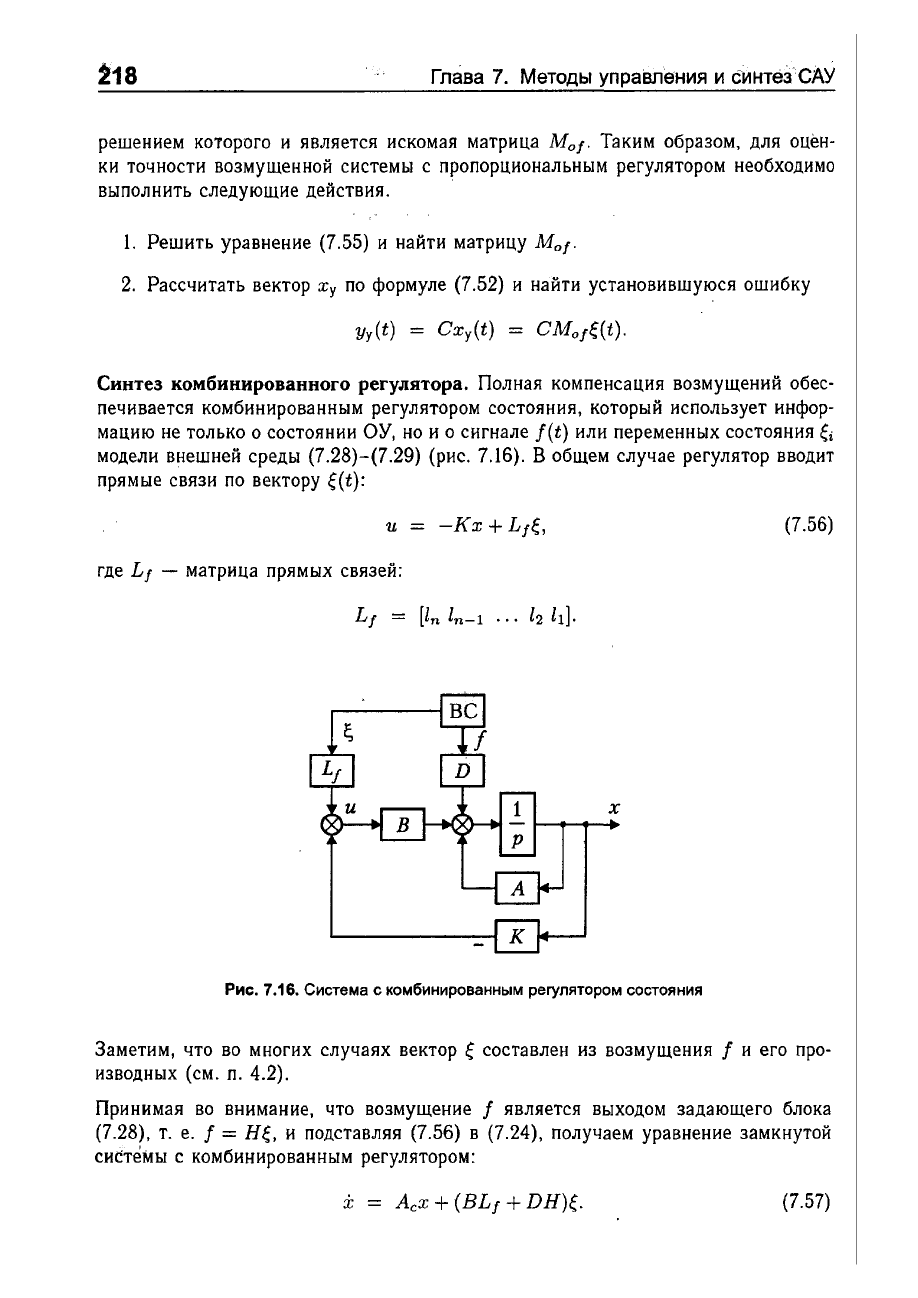
Синтез
комбинированного
регулятора.
Полная
компенсация
возмущений
обес
печивается
комбинированным
регулятором
состояния,
который
использует
инфор
мацию
не
только
о
состоянии
ОУ,
но
и о
сигнале
f(t)
или
переменных
состояния
~i
модели
внешней
среды
(7.28)-(7.29)
(рис.
7.16).
В
общем
случае
регулятор
вводит
прямые
связи по
вектору
~(t):
u =
-Кх+Lf~,
(7.56)
где
Lf
-
матрица
прямых
связей:
х
Рис.
7.16.
Система
с
комбинированным
регулятором
состояния
Заметим,
что
во
многих
случаях
вектор
~
составлен
из
возмущения
f
и
его
про
изводных
(см.
п.
4.2).
Принимая
во
внимание,
что
возмущение
f
является
выходом
задающего
блока
(7.28),
т.
е.
f =
H~,
и
подставляя
(7.56)
в
(7.24),
получаем
уравнение
замкнутой
системы
с
комбинированным
регулятором:
(7.57)
7.3.
-Регуляторы
и
системы
управления
состоянием
219
в
частном
случае
матрица
L f
может
быть
получена
как
решение
матричного
урав-
нения
BLf+DH
=
О.
(7.58)
Тогда
система
(7.57)
принимает
вид
(7.34),
ее
поведение
не
зависит
от
возмущения,
Н,
следовательно,
обеспечивается
абсолютная
точность
стабилизации
в
ТОЧКе
х·
=
=
О,
т.
е.
Х
у
=
О и
'уу
=
о.
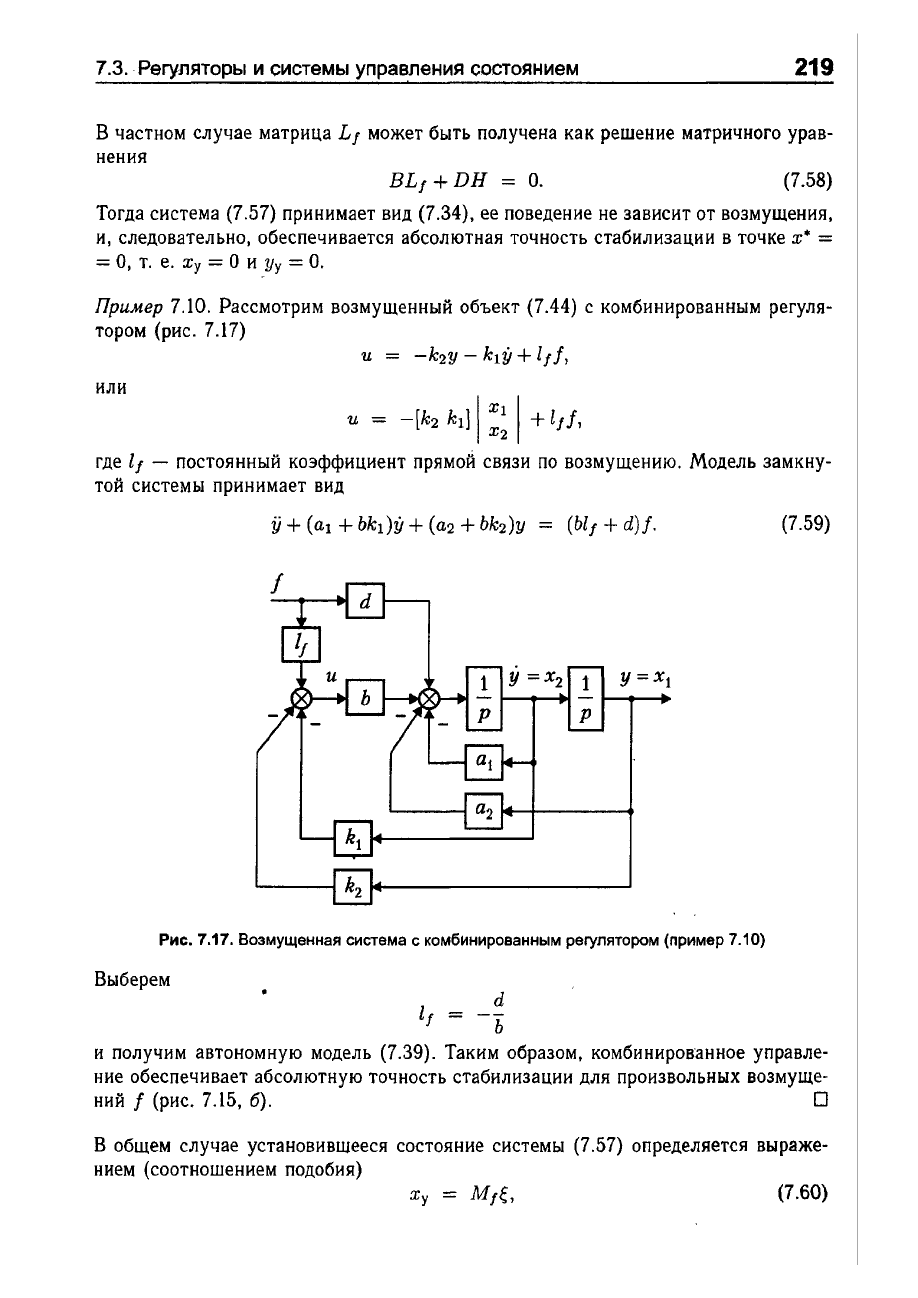
Прuмер
7.10.
Рассмотрим
возмущенный
объект
(7.44)
с
комбинированным
регуля
тором
(рис.
7.17)
или
и
=
-[k
2
k,] I
~~
I +
Ы,
где
1 f -
постоянный
коэффициент
прямоЙ
связи
по
возмущению.
Модель
замкну
той
системы
принимает
вид
Рис.
7.17.
Возмущенная
система
с
комбинированным
регулятором
(пример
7.10)
Выберем
d
Ь
(7.59)
и
получим
автономную
модель
(7.39).
Таким
образом,
комбиниров-анное
управле
ние
обеспечивает
абсолютную
точность
стабилизации
для
произвольных
возмуще
ний
f
(рис.
7.l5,
б).
О
В общем
случае
установивщееся
состояние
системы
(7.57)
определяется
выраже
нием
(соотношением
подобия)
(7.60)
