Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.


180
Глава
6.
КачеСТВО.системуправления
Тогда по
теореме
подобия
(свойство
6.1)
соответствующие
переходные
функции
системы
(6.65)
находятся
как
(6.70)
т.
е.
при
""о
> 1
получаются
сжатием
h1(t)
по оси
времени
t
(рис.
6.17).
При
этом
величина
перерегулирования
cr
остается
прежнеЙ
r
а
время
переходного
процесса
определяется
по
формуле:
(6.71)
о
t
Рис.
6.17.
Деформация
(сжатие)
переходных
функций
при
увеличении
параметра
""о
6.З.2.~;liIмbмиальное
разложение
и
переходные
функции
Биномиальное
разложение
задается
формулой
(биномом)
Ньютона:
( )
n +
n-l
+ +
n-l
n
(+)n
а
Р
=
Р
al""Op
• . .
an-l""О
Р
+
""о
=
Р
""о
,
(6.72)
где
""о
-
положительное
число,
ai
-
биномиальные
коэффициенты.
Полиномы
1-6-ro
порядков,
построенные
на
базе
бинома
Ньютона,
приведены
в
табл.
6.3.
Таблица
6.3.
Биномиальные
разложения
n
Вид
полинома
1
Р
+
""о
2
р
2
+
2""ор
+
""б
3
р3
+
З""ор
2
+
&vБР
+
""~
4
р4
+
4""ор3
+
6""
бр
2
+
4",,3р
+
""3
5
р5
+
5""ор
4
+
10""БР
3
+
lО",,3
р
2
+
5""Зр
+
ш8
6
р6
+
6",,(}р5
+
15w~p4
+
2Ош3р
3
+
15""3р
2
+
вW8p
+
""8
6.3.
Метод
стандартных
переходных
'функций
hl~~---r--т-~~-т--~--т-~~-т--~
1,25
1,0
0,75
0,5
0,25
о
2
4
3
2
n=1
6 8
6
5
4
10
12
14
16
18
t,
с
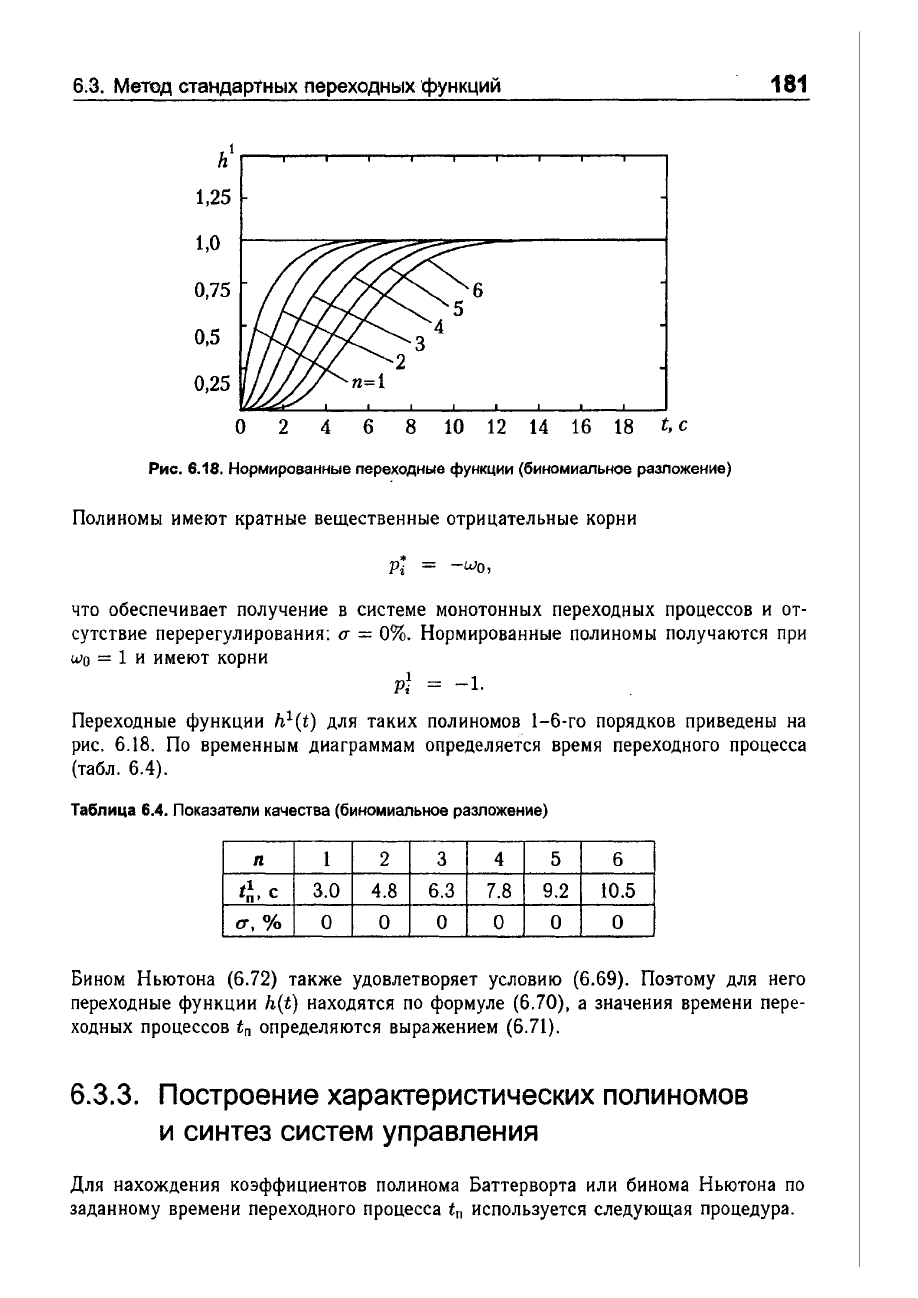
Рис.
6.18.
Нормированные
переходные
функции
(биномиальное
разложение)
Полиномы
имеют
кратные
вещественные
отрицательные
корни
181
что
обеспечивает
получение
в
системе
монотонных
переходных
процессов
и
от
сутствие
перерегулирования:
а
=
0%.
Нормированные
полиномы
получаются
при
Wo
= 1
и
имеют
корни
р}
=
-1.
Переходные
функции
h
1
(t)
для
таких
полиномов
1-6-го
порядков
приведены
на
рис.
6.18.
По
временным
диаграммам
определяется
время
переходного
процесса
(табл.
6.4).
Таблица
6.4.
Покаэатели
качества
(биномиальное
разложение)
n
1
2
3
4 5 6
t~,
с
3.0
4.8
6.3
7.8
9.2
10.5
0',
%
о о о о о о
Бином
Ньютона
(6.72)
также
удовлетворяет
условию
(6.69).
Поэтому
для
него
переходные
функции
h(t)
находятся
по
формуле
(6.70),
а
значения
времени
пере
ходных
процессов
t
n
определяются
выражением
(6.71).
6.3.3.
Построение
характеристических
полиномов
и
синтез
систем
управления
для
нахождения
коэффициентов
полинома
Баттерворта
или
бинома
Ньютона
по
заданному
времени
переходного
процесса
t
n
используется
следующая
процедура.
182
'Глава
6.
Качество
систем-управления
1.
По
нормированным
переходным
функциям
или
таблицам
определяется
зна
чение
t~.
2.
Минимально
допустимый
радиус
распределения
корней
(.1)0
находится
по
фор
муле
(следует
из
выражения
(6.71»
(6.73)
3.
Коэффициенты
ai(.l)b
искомого
полинома
а(р)
определяются
по
формулам
(6.68)
или
(6.72),
где
значения
ai
находятся
по
соответствующим
таблицам.
Прuм,ер
6.1.
Рассмотрим
задачу
синтеза
алгоритма
управления
(регулятора),
обес
печивающего
стабилизацию
объекта
второго
порядка
в
точке
у
=
у*
с
заданными
показателями
качества.
ОУ
(см.
пример
2.1
и рис.
6.19)
описывается
дифференци
альным
уравнением
y(t) + alOy(t) + a20y(t)
~
bu(t)
(6.74)
или,
в
оператор
ной
форме,
-
i
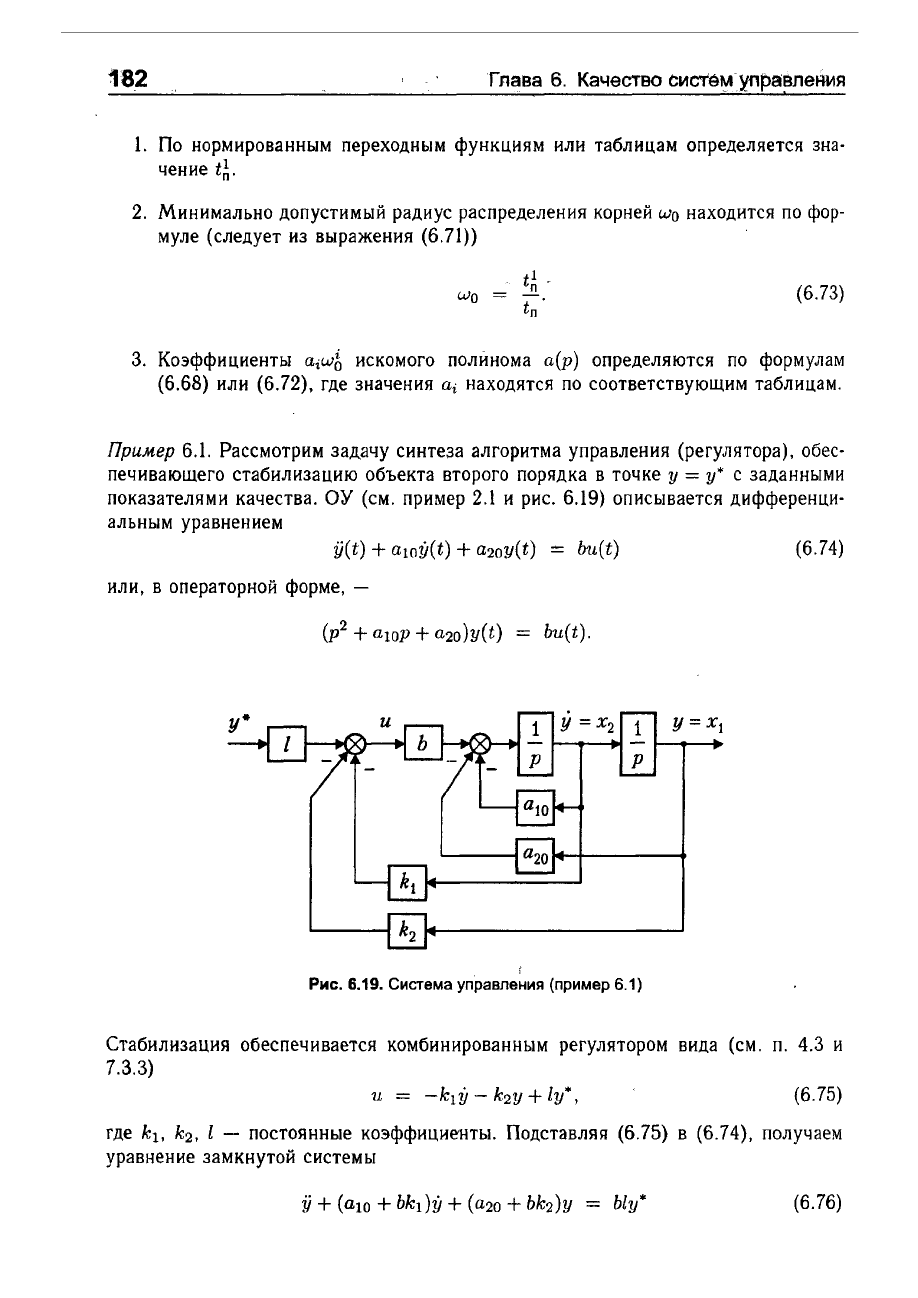
Рис.
6.19.
Система
управления
(пример
6.1)
Стабилизация
обеспечивается
комбинированным
регулятором
вида
(см.
п.
4.3
и
7.3.3)
и
=
-k
1
y - k
2
y +
[у*,
(6.75)
где
k
1
,
k
2
,
l -
постоянные
коэффициенты.
Подставляя
(6.75)
в
(6.74),
получаем
уравнение
замкнутой
системы
(6.76)

6~3.
Метод
стандартных
переходных
функций
183
с
характеристическим
полиномом
(6.77)
Условие
(6.66),
при
котором
обеспечивается
абсолютная
точность
стабилизации,
т.
е.
Уу
=
у*,
выполняется,
если
выбрать
(6.78)
а
заданные
динамические
показатели
качества
(J
и
t
n
определяются
выбором
коэф
фициентов
k
1
и
k
2
•
Для
этого
по
рассмотренной
выше
методике
нужно
отыскать
коэффициенты
подходящего
типового
полинома
второго
порядка
(6.79)
и
приравняв
(6.77)
и
(6.79),
получить
искомые
значения
коэффициентов
обратной
связи:
(6.80)
Рассмотрим
простой
частный
случай,
для
которого
аl
=
1,
а2
=
О,
Ь
=
1,
и
две
задачи
стабилизации
системы
с
заданным
временем
переходных
процессов
и
перегулированием:
а)
б)
t
n
= 1
с
'
(J
::;
5
%;
(J
= 0%.
Воспользуемся
регулятором
(6.75).
Уравнение
замкнутой
системы
(6.76)
для
рас
сматриваемого
случая
принимает
вид
(6.81)
и
имеет
характеристический
полином
(6.82)
Из
формулы
(6.78)
получаем
(6.83)

184
Глз'ва
6.
Качество'
систем
управления
в
задаче
(а)
для
нахождения
коэффициентов
регулятора
(6.75)
используется
по
лином
Баттерворта
второго
порядка
(n =
2),
обеспечивающий
получение
перере
гулирования
а
= 4.5%
(см.
табл.
6.2).
По
той
же
таблице
находим
номинальное
время
переходного
процесса
t~
= 2.9
с,
а
по
формуле
(6.73) -
радиус
распределения
корней
""о
=
t~/tn
= 2.9.
Искомый
полином
принимает
вид
(см.
(6.68)
или
табл.
6.1)
а(р)
=
р2
+
4.10р
+ 8.41
и
имеет
корни
Pl,2
=
-2.051=
j2.05.
Сравнивая
(6.82)
и
(6.85),
находим
k
1
= 3.10, k
2
= 8.41.
(6.84)
(6.85)
Переходные
функции
системы
с
номинальным
полиномом
Баттервота
h'(t)
и
син
тезированной
системы
h(t)
представлены
на
рис.
6.20.
у
1
h(t)
h
(t)
о
1 2 3 4
t,
с
Рис.
6.20.
Переходные
функции
системы
2-го
порядка
(полином
Баперворта)
в
задаче
(б)
для
нахождения
коэффициентов
регулятора
(6.75)
используется
би
ном
Ньютона
второго
порядка
(n =
2),
обеспечивающий
получение
монотонного
переходного
процесса
(а
= 0%).
По
табл.
6.4
находим
t~
= 4.8
с,
а
по
формуле
(6.73) -
радиус
распределения
корней
""о
=
t~/tn
= 4.8.
Искомый
полином
принимает
вид
(см.
(6.72)
или
табл.
6.3)
а(р)
=
р2
+
9.60р
+ 23.04
(6.86)

6.4.
Оценка
точностных
показател~~
1&5
у
h(t)
h\t)
о
2 4
6
t
Рис.
6.21.
Переходные
функции
системы
второго
порядка
(биномиальное
разложение)
и
имеет
равные
корни
Рl,2
=
-4.80.
Сравнивая
(6.82)
и
(6.86)
находим
k
1
= 8.60, k
2
= 23.04.
Переходные
функции
системы
с
номинальным
полиномом
h
1
(t)
и
синтезированной
системы
h(t)
представлены
на
рис.
6.21.
О
6.4.
Оценка
точностных
показателей
Как
было
показано
в
подразделе
6.1.3,
точностные
показатели
системы
управле
ния
оцениваются
по
установившимся
составляющим
переходных
процессов
yy(t)
и
ey(t).
Поведение
конкретной
системы
в
установившемся
режиме
зависит
от
ее
параметров,
типа
входных
воздействий
y*(t}
и
возмущений
f(t),
а
также
структур
ных
особенностей
системы.
Последние
опредедяются
наличием
или
отсутствием
обратных
связей
и
порядком
астатизма
основной
части
системы
(см.
также
2.4.2,
4.3.2
и
п.
7.2).
6.4.1.
Разомкнутые
и
замкнутые
си'стемы
управления
Сначала
рассмотрим
разомкнутую
систему
управления,
т.
е.'
систему,
состоящую
из
последовательно
соединенных
регулятора
и
объекта
управления
и
не
содержащую
обратных
связей
(рис.
6.22).
Пусть
объект
управления
описывается
операторным
уравнением
y(t)
= Wo(p)u(t) +
Wf(p)f(t),
(6.87)
а
регулятор
представлен
выражением
u(t)
=
K(p)y*(t),
(6.88)
.
где
y(t) -
выходная
переменная,
u(t)
-
управляющее
воздействие,
f(t)
-
возму
щающее
воздействие.
Уравнение
системы
принимает
вид
y(t)
=
W(p)y*(t)
+
Wf(p)f(t),
(6.89)

186
rIJasa 6.
Качество
систем
управления
f
у*
у
Рис.
6.22.
Разомкнутая
система
где
W(p) = K(P)W.(P) =
~~~,
Wf(P) =
:~~
(6.90)
-
передаточные
функции
разомкнутой
системы
по
задающему
и
возмущающему
воздействиям,
а(р),
Ь(р),
d(p)
-
дифференциальные
операторы
соответствующих
степеней.
Теперь
рассмотрим
замкнутую
систему
управления
(рис.
6.23),
представленную
объектом
управления
(6.87)
и
простейшим
регулятором
отклонения
u(t) = K(p)e(t),
(6.91)
где
e(t) = y*(t) - y(t).
(6.92)
f
у*
Рис.
6.23.
Замкнутая
система
После
подстановки
последних
выражений
в
(6.87)
и
простых
преобразований
на
ходим
модель
замкнутой
системы
y(t) =
Ф(р)у*(t)
+
Фf(р)f,
(6.93)
где
Ф(р)
-
передаточная
функция
замкнутой
системы
по
задающему
воздействию,
определяемая
как
K(p)Wo(p)
Ф(р)
= 1 + K(p)Wo(p)
=
W(p)
1 + W(p) ,
(6.94)
а
Фf(Р)
-
передаточная
функция
замкнутой
системы
по
возмущающему
воздей
ствию,
определяемая
как
Wf(p)
=
1 +
W(p)'
(6.95)

6.4",
"Оценка'
точностных
Rокаэателе".
"_
Учитывая
(6.90),
нетрудно
получить
где
Ф(Р)
=
Ь(Р)
,
Фf(Р)
ас(р)
d(p)
==
ас(р)
,
ас(р)
=
а(р)
+
Ь(р)
-
характеристический
полином
замкнутой
системы.
187
(6.96)
Сравнение последних
выражений
с
(6.90)
показывает,
что
замыкание
системы
приводит
к
изменению
знаменателя
ее
передаточных
функций,
т.
е.
характери
стического
полинома
системы.
Это,
в
частности,
и
обеспечивает
улучшение
ее
точностных
показателеЙ.
При
определенных
условиях
установившиеся
значения
выходной
переменной
у,
а
также
ошибки
е
легко
получить,
используя
известные
правила
(см.
2.2.5).
Пусть
входные
воздействия
рассмотренных
систем
управления
изменяются
достаточно
медленно,
т.
е.
y*(t)
==
const,
f(t)
==
const,
а
передаточные
функции
W(p), Wf(p)
и
Ф(р),
Фf(Р)
определены
в
точке
р
=
О.
Тогда
для
разомкнутой
системы
(6.89)
имеет
место:
yy(t)
~
W(O)y*(t) +
Wf(O)f(t),
(6.97)
а
для
замкнутой
системы
(6.93) -
Yy(t)
=
Ф(О)у*(t)
+
Фf(О)f(t),
(6.98)
соответствующие
значения
ошибки
ey(t)
находятся
по
формуле
(6.92) .
Основными
препятствиями
для
использован,ИЯ
формул
(6.97)-(6.98)
являются
быстрые
изменения
входных
переменных
и
вырожденность
соответствующих
пере
даточных
функций
(особенно
для
разомкнутых
систем).
Последнее
свойство
свя
зано
с
понятием
астатизма
(см.
также
подраздел
2.2.5).
6.4.2.
Статические
и
астатические
системы
Рассмотрим
динамиче~кую
систему
с
одним
входным
воздействием:
где
и
y(t) = W(p)y*(t),
W(p)
Ь(р)
=
а(р)
а(р)
=
рn
+
alpn-l
+ ... +
an-lР
+
а
n
,
Ь(р)
=
b1pn-l
+ ... +
bn-lР
+
Ь
n
.
(6.99)
(6.100)

188
Глава
6.
Качество
систем
управления
Будем
полагать,
что
в
данном
случае
в
качестве
входа
у*
(t)
может
выступать
как
задающее,
так
и
возмущающее
воздействие
f(t),
а
под
системой
(6.99)
подразу
мевается
как
разомкнутая
система
типа
(6.89),
так
и
основная
часть
замкнутой
системы
(6.93).
В
подразделе
2.2.5
установлено,
что
для
статической
системы,
т.
е.
при
ан
=f:.
О,
значение
передаточной
функции
в
точке
р
=
О
определяется
как
Ь
n
W(O) = - =
К,
а
n
где
К
-
статический
коэффициент
системы,
и
при
ПОСТОЯННОМ'
входном
воздей
ствии
у*
= const
имеет
место
Уу
=
Ку*.
Отметим,
что
для
статической
системы
характеристическое
уравнение
а(р)
=
О
не
имеет
нулевых
корней.
Теперь
рассмотрим
астатическую
систему,
полагая,
что
Ее
характеристическое
уравнение
может
быть
приведено
к
виду
а(р)
=
р";а,,;(р)
=
О,
где
( )
n-,,;
n-,,;-l
а,,;
р
=
р
+
alP
+ ... +
а
n
-,,;-1Р
+
а
n
-,,;,
и
имеет
к
нулевых
корней.
Число
к
называется
порядком
астатuзма.
Для
аста
тической
системы
можно
записать
(рис.
6.24»
где
1
W(p) = r
W,,;(P)
,
Ь(р)
Wtt{p) = att{p) ,
и
поэтому
характерным
признаком
астатизма
служит
соответствующее
число
ин
тегрирующих
звеньев:
к
>
О.
у.
~~1
У
=---.t
w
(р)
- -- - -
1с
Р
Р
Р
к
Рис.
6.24.
Астатическая
система

6.4.
Оценка
ТОЧНОСТНЫХ
показателей
189
Так
как
для
астатической
системы
значение
W(O)
не
определено,
то
можно
ввести
в
рассмотрение
показатель
Ь
n
W~(O)
= - =
K~,
a~
называемый
добротностью
системы
по
соответствующей
производной
выходной
переменной
(по
скорости,
ускорению
и
т.
д.).
Для
случая
медленно
изменяющегося
входного
сигнала
у*
им"еет
место
простая
зависимость:
y~~)
=
W~(O)y*
=
Кк,У*,
которая,
в
частности,
показывает,
что
функция
Yy(t),
а
следовательно,
и
E'y(t)
является
неограниченно
возрастающей
или
убывающей.
Отметим,
что
астатизм
системы
управления
может
быть
обусловлен
свойства
ми
объекта
управления
(см.
п.
6.1)
или
наличием
в
ее
составе
пи-
и
пид
регуляторов.
6.4.3.
Точность
при
постоянных
входных
воздействиях
Сначала
рассмотрим
системы
управления
при
у*
= const
и
нулевом
возмущающем
воздействии:
f =
О.
ДЛЯ
разомкнутой
системы
(6.99)
в
установившемся
режиме
имеем:
Уу
= W(O)y*.
(6.101)
Если
система
статическая,
то
получаем
известную
формулу
Уу
=
Ку*,
(6.102)
и
установившаяся
ошибка
определяется
как
Е'у
=
(1-
К)у*
(рис.
6.25,
а).
Очевидно,
что
нулевое
значение
ошибки
Е'у
и,
следовательно,
абсо
лютная
точность
системы
достигается
при
К
=
1.
Для
астатической
системы
в
силу
свойств,
полученных
в
6.4.2,
установившиеся
значения
выходной
переменной
и
рассогласования
не
определены
(рис.
6.25,
б).
Модель
замкнутой
системы
принимает
вид
(6.93),
и
в
установившемся
режиме
при
указанных
выше
условиях
получаем:
Уу
=
Ф(О)у*.
(6.103)
Если
в
разомкнутом
виде
рассматриваемая
система
является
статической,
то
Ф(О)
=
ФО
= 1
+КК
=
Ь
N
а
n
+
Ь
n
'
