Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.


Глава
6.
Качество
систем управления
приводит
к
пропорциональному
сжатию
графиков
переходных
процессов
вдоль
оси
времени
t
(рис.
6.9).
Естественно,
что
для
систем
с
большим
значением
Wo
обес
печивается
более
быстрое
затухание
всех
составляющих
выходной
переменной,
т.
е.
более
высокое
быстродействие.
При
этом
остальt-Iые
показатели
системы,
ха
рактеризующие
колебательные
свойства
процессов
(перерегулирование,
затухание
и
т.
д.)
не
изменятся.
Используя
введенное
в
Пiдразделе
6.1.4
понятие
времени
переходного
процесса,
запишем
следующий
результат,
являющийся
прямым
след
ствием
теоремы
подобия.
у'
y(t)
уо
о
Рис.
6.9.
Деформация
(сжатие)
переходных
процессов
при
увеличении
параметра
Wo
Свойство
6.2.
Время
переходного
процесса
системы
(6.34)
с
полюсами
P~
=
wOPi
определяется
выражением
t' =
~
n ,
Wo
(6.40)
где
t
n
-
время
переходного
процесса
системы
(6.29),
а
показатели
колебательности
не
зависят
от
wo.
Таким
образом,
время
переходного
процесса
системы
увеличивается
при
удалении
ее
полюсов
от
границы
устойчивости
(мнимой
оси).
Полученные
зависимости
дают
возможность
производить
сравнительный
анализ
систем
управления,
для
которых
корни
связаны
соотношением
(6.36),
и
находить значения
показателей
качества
при
условии,
что эти
показатели
известны
для
номинальной
системы
(6.29),
т.
е.
при
Wo
= 1
(см.
п.
6.3).
6.2.2.
Анализ
быстродействия
Для
количественной
оценки
быстродействия
конкретной
системы
(и.
нахождения
времени
переходного
процесса)
используется
понятие
степени
устойчивости.
Рассмотрим
один
или
несколько
ближайших
к
мнимой
оси
(границе
устойчивости)
полюсов
рТ
асимптотически
устойчивой
системы.

6.2.
Корневые
методы
исследования
качества
171
Степенью
устойчивости
системы
называется
положительное
число
а*
= -
тах
Re Pi, i =
1,
n,
i
(6.41)
соответствующее
расстоянию
от
мнимой
оси
до
ближайшего
к
ней
корня
pi,
или
1т
о
I
р*
а*
о
о
Re
а*
=
-Re
р;.
(6.42)
Учитывая,
что
скорость
протекания
процессов
возраста
ет
при
удалении
корней
от
мнимой
оси
(см.
6.2.l),
можно
заключить,
что
степень
устойчивости
характеризует
быст
родействие
системы.
Для
выявления
связи
степени
устойчивости
с
быстродей
ствием
системы
рассмотрим
выражение
(6.32)
и
выделим
составляющие
переходного
процесса
Yi(t),
соответствую
щие
вещественным
или
комплексным
значениям
корней
рТ.
Пусть
условию
(6.42)
удовлетворяет
ОДl1Н
вещественный
корень
р*
=
-а*.
Рассмотрим
апериодическую
составляющую
(см.
5.2.,2
и
рис.
6.10)
y*(t)
=
C*e-
cx
•
t
,
(6.43)
(6.44)
которая
в
силу
условия
(6.41)
является
наиболее
медленной
составляющей
пе
реходного
процесса
системы.
Определим
соответствующее
ей
время
переходного
процесса
t~.
При
t =
t~
выражение
(6.44),
принимает
вид
(6.45)
с
другой
стороны,
учитывая
определение
времени
переходного
процесса,
где
для
рассматриваемого
случая
д
п
=
д
п
'у*
(О)
I =
дпС*,
запишем
y*(t~)
=
д
п
=
дпС*.
у*
С*
о
t*
п
t
Рис.
6.10.
Апериодическая
составляющая
и
оценка
быстродействия

172
Глава
6.
Качество
систем
управлени,
Тогда,
сопоставляя
последние
два
выражения,
находим
И,
логарифмируя,
получаем
искомое
значение
*
111
t
n
= -
пт·
а*
ип
Для
случая,
когда
д
п
=
0.05,
учитывая,
что
ln
20
~
3,
находим
1т
а*
О
Re
t*
с::!
~
n -
а*
(6.47]
Теп~рь
рассмотрим
случай,
когда
условию
(6.42)
удовле
творяет
пара
комплексно~сопряженных
корней
pi,2 =
-а*
=f
j(3*.
Соответствующая
колебательная
составляющая
(см.
5.2.2
и
рис.
6.11)
y*(t) =
A*e-
a
"
t
sin((3*t+<p), (6.48)
в
силу
условия
(6.41)
является
наиболее
медленной
составляющей
переходного
npottecca
системы.
Определим
отвечающее
ей
время
переходного
процесса
t~,
при-
нимая
во
внимание,
что
Так
как
мажоранта
A*e-
a
"
t
колебательного
процесса
y*(t)
совпадает
с
рассмотрен
ной
ранее
апериодической
составляющей
(6.44),
то
для
нее
справедливы
формулы
(б.46)
и
(6.47).
Следовательно,
для.
самой
функции
y*(t)
выполняется
неравенство
у*
А*
о
-А*
t* < ..!.-ln
~
n -
а*
д
п
'
t
Рис.
6.11.
Колебательная
составляющая
и
оценка
быстродействия
(6.49)

6.2.
Корневые
методы
исследования
качества
173
и
при
д
n
=
0.05
-
3
t~
::;
а*
(6.50)
Полученные
выражения
(6.49)-(6.50)
и
(6.46)-(6.47)
определяют
времена
пере
ходных
процессов,
соответствующие
самым
медленным
составляющим
выходной
переменной
y(t).
Так
как
на
быстродействие
системы
влияют
и
другие
моды
Yi(t),
то
значение
времени
переходного
процесса
t
n
в
общем
случае
оказывается
боль-
шим,
чем
t~,
т.
е.
3
t
n
>
-.
-
а*
Несмотря
на
это
формулы
(6.49)-(6.50)
и
(6.46)-(6.47)
часто
используются
для
грубой
оценки
быстродействия
системы.
Они
становятся
более
точными
при
зна
чительном
удалении
от
р*
остальных
корней
системы
и
абсолютно
неприемлемы
для
случая,
когда
ближайшими
к
мнимой
оси
оказываются
несколько
равных
ве
щественных
полюсов
Pi
(см.
6.3.2).
6.2.3.
Оценка
колебательности
Если
все
полюсы
системы
имеют
вещественные
значения,
то
все
состаsmпощие
пе
реходного
процесса
(6.32)
имеют
апериодический
характер.
Колебательность
про
цессов
появляется при
наличии
комплексных
корней.
Для
количественной
оценки
колебательных
свойств
системы
используется
понятие
степени
колебательности.
1т
о
-(3
Re
Выделим
сектор
размера
21/;,
в
котором
расположены
полюсы
устойчивой
системы,
и
рассмотрим
«крайние»
корни,
лежащие
на
границах
(лучах
сектора):
Pi,2 =
-а
=F
j{3,
где
а
>
О
И
{3
>
О.
(6.51)
Степенью
коле6ательности
устойчивой
системы
на-
зывается
положительное
число
{3
f."
=
~.
Указанное
число
связано
с
размером
сектора
по
формуле
Ф
=
arctg
J1..
Учитывая,
что
колебательность
процессов
возрастает
при
удалении
корней
от
веще
ственной
оси
(увеличении
Ф
и
(3),
можно
предположить,
что
число
J.L
характеризует
колебательные
свойства
системы.
Проанализируем
поведение
колебательной
составляющей
y*(t) =
А
e-
at
sin({3t +
<р),
(6.52)
174
Глава
6.
Качество
систем
управления
соотвествующей
паре
комплексно-сопряженных
корней
(6.51).
Число
(3
(коэффи
циент
при
мнимой
части
корней
pi,2)
равно
угловой
частоте
колебаний.
При
доста
точно
малых
значениях
(3,
а
следовательно,
и
показателя
fl,
имеют
место
низко
частотные
процессы,
близкие
к
апериодическим.
При
увеличении
(3
и
fl
увеличи
вается
частота
процессов
и
число
колебаний
системы
за
тот
же
интервал
времени
t
n
= 3/0..
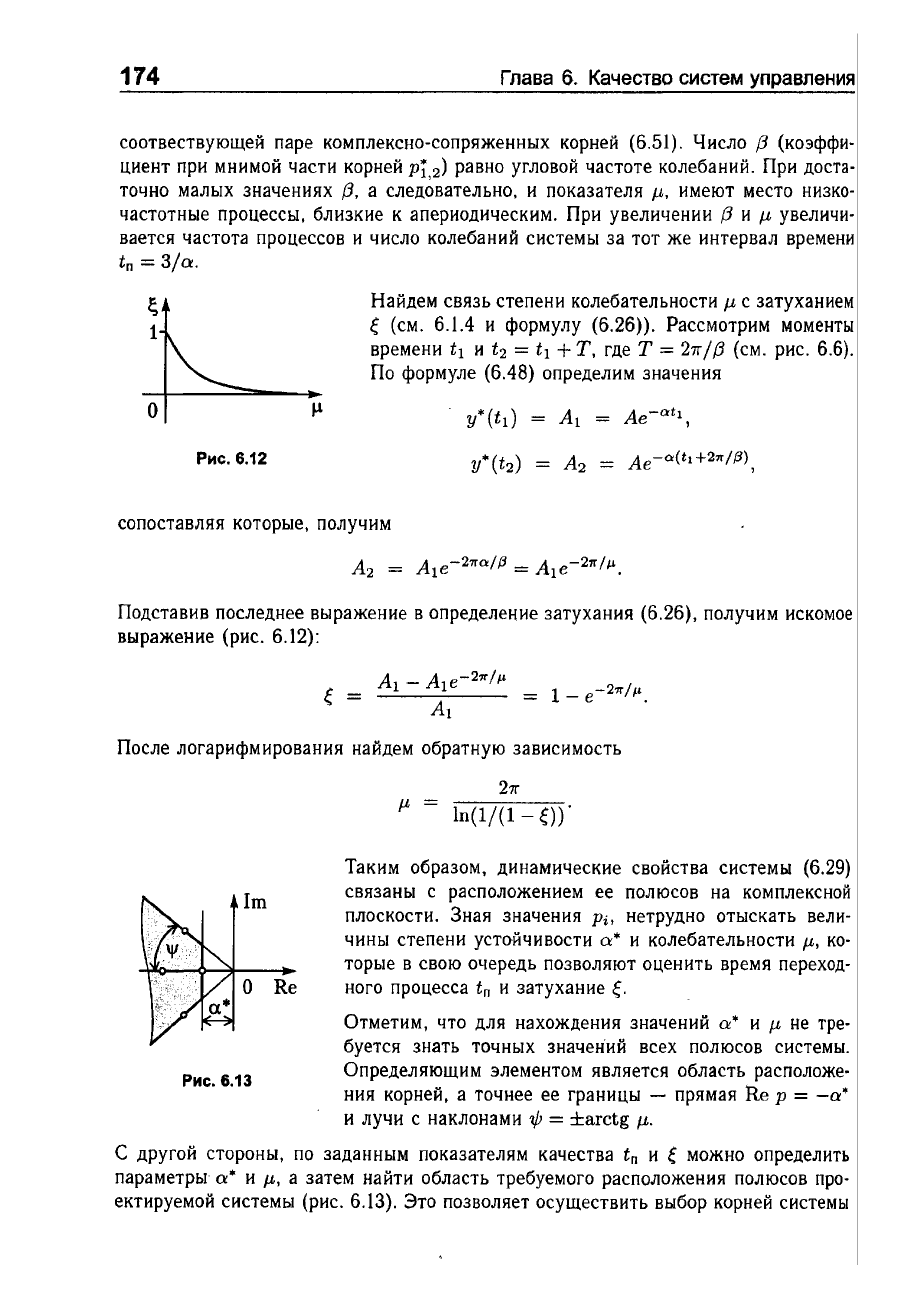
l;
1
о
Рис.
6.12
Найдем
связь
степени
колебательности
fl
с
затуханием
~
(см.
6.1.4
и
формулу
(6.26)).
Рассмотрим
моменты
времени
t
1
и
t
2
= t
1
+
Т,
где
Т
=
27r
/
(3
(см.
рис.
6.6).
По
формуле
(6.48)
определим
значения
y*(t
1
)
=
А
1
=
Ae-
at1
,
у*
(t2) =
А
2
=
Ae-
a
(tl
+211"/.8),
сопоставляя
которые,
получим
Подставив
последнее
выражение
в
определение
затухания
(6.26),
получим
искомое
выражение
(рис.
6.12):
После
логарифмирования
найдем
обратную
зависимость
1т
о
Re
Рис.
6.13
27r
fl
=
ln(l/(l
_
~))'
Таким
образом,
динамические
свойства
системы
(6.29)
связаны
с
расположением
ее
полюсов
на
комплексной
плоскости.
Зная
значения
Pi,
нетрудно отыскать
вели
чины
степени
устойчивости
0.*
и
колебательности
fl,
ко
торые
в
свою
очередь
позволяют
оценить
время
переход
ного
процесса
t
n
и
затухание
~.
Отметим,
что
для
нахождения
значений
а*
и
fl
не
тре
буется
знать
точных
значений
всех
полюсов
системы.
Определяющим
элементом
является
область
расположе
ния
корней,
а
точнее
ее
границы
-
прямая
Re
Р
=
-а*
и
лучи
с
наклонами
Ф
= ±arctg fl.
С
другой
стороны,
по
заданным
показателям
качества
t
n
и
~
можно
определить
параметры'
0.*
и
fl,
а
затем
найти
область
требуемого
расположения
полюсов
про
ектируемой
системы
(рис.
6.13).
Это
позволяет
осуществить
выбор
корней
системы

6.2.
Корневые
мет-оды
исследования
качества
175
Pi
при
решении
задач
синтеза
регуляторов
с
использованием
модаJlЬНЫХ
методов
(см.
7.3.l).
В
ряде задач
синтеза
требуется
построить
систему
по
заданным
показателям
t
n
и
а,
связанным
со
свойствами
переходных
характеристик.
В
этом
случае
требуемые
значения
корней
определяются
с
использованием
метода
стандартных
переходных
функций
(см.
п.
6.3).
6.2.4.
Оценка
быстродействия
по
норме
вектора
состояния
Осуществим
оценку
быстродействия
динамической
системы
(6.l8),
решение
кото-
рой
имеет
вид
(6.53)
Переходный
процесс
x(t)
определяется
свойствами
матрицы
А
и
в
первую
очередь
ее
собственными
числами
>ч{А}
=
Pi.
Для
асимптоти:ески
устойчивой
системы
выполняется
Re
,,\{А}
'<
О,
i =
г,n,
(6.54)
и
(как
следует
из
результатов,
приведенных
в
6.2.1)
чем
меньшие
значения
при
нимают
вещественные
част~
собственных
чисел,
тем
выше
скорость
затухания
процесса.
Быстродействие
системы
(6.l8)
связано
с
понятием
степени
устойчивости,
под
которым
(аналогично
понятию,
введенному
в
6.2.2)
подразумевается
положитель-
ное
число
а*
= -
т~
Re
Лi
{А},
i =
1,
n.
(6.55)
t
Для
количественной
оценки
быстродействия
устойчивой
системы
(6.l8)
и
нахож
дения
времени
переходных
процессов
x(t)
используется
следующее
положение,
непосредственно
вытекающее
из
свойства
5.5,а
(см.
5.2.3)
и
связанное
со
свой
ством
экспоненциальной
устойчивости
(см.
5.1.2). ,
Введем
в
рассмотрение
взвешенную
евклидову
норму
вектора
состояния
вида
Ix(t)lp = J
xT(t)Px(t),
где
Р
=
рТ
>
О
-
весовая
матрица.
Свойство
6.3.
Если
собственные
числа
матрицы
А
удовлетворяют
условию
Re
Лi{А}
< -
а,
i =
г,n,
(6.56)
то
найдется
матрица
Р
=
рТ
>
О
такая,
что
для
любых
t >
О
(6.57)

Глава
6.
Качество
систем
управления
Свойство
6.3
устанавливает
экспоненциальную
устойчивость
системы·
(по
некото
рой
взвешенной
норме)
с
пара
метром
а,
который
определяет
скорость
затухания
процессов.
Параметр
зависит
от
расположения
собственных
чисел
Ai{A}
на
ком
плексной
плоскости
и
выбирается
меньшим,
чем
степень
устойчивости,
т.
е.
а
<
а*.
(6.58)
Замечание
6.4.
В
соответствии
со
свойством
5.5,а
при
условии
(6.56)
весовая
матрица
Р
>
о
находится
как
решения
алгебраического
уравнения
(5.42).
Из
формулы
(6.57)
следует,
что
для
любых
начальных
значений
из
произвольной
до-окрестности:
Ixolp
::;
до
имеет
место
неравенство
(рис.
6.14)
Ix(t)lp <
дое-
аt
•
Зададим
число
д
п
=
Опдо,
(6.59)
(6.60)
где
О
<
б
п
<
1,
и
найдем
время
переходного
процесса
t
п
,
за
которое
все
фазовые
траектории
системы,
начинающиеся
в
области
(6.59),
попадают
в
дп-окрестность
'noлoжения
равновесия,
т.
е.
выполняется:
для
этого
рассмотрим
мажоранту
переходных
процессов,
определенную
выраже
нием
(6.60),
т.
е.
апериодический
процесс
л
-at
u.o
е
.
(6.61)
в
соответствии
с
результатами,
представленными
в
6.2.2,
время
переходного
про
цесса
для
мажоранты
определяется
формулой
о
* 1 1 1
t
n
= -
nT'
а
uп
t*
п
t
Рис.
6.14.
Оценка
быстродействия
по
вектору
состояния
(6.62)

6.З.
Метод
стандартных
переходных
функций
Так
как
искомое
значение
t
n
всегда
меньше
t~,
то
получаем
а
для
случая,
когда
д
п
= 0.05, -
1 1
t
n
<
-ln-
а
д
п
'
3
t
n
<
177
(6.63)
(6.64)
Отметим,
что
полученные
выше
значения
верхней
границы
t
n
характеризуют
ди
намику
вектора
состояния
для
всех
начальных
значений
из
области
(6.59),
что
является
несомненным
достоинством
оценок
(6.63)
и
(6.64).
Однако
при
этом
рас
сматривается
затухание
процессов
по
некоторой
взвешенной
норме,
и
поэтому
указанные
выше
окрестности
положения
равновесия
не
являются
круговыми.
Бо
лее
того,
их
форма
зависит
от
выбора
числа
а
и
его
близости
к
степени
устойчиво
сти
а*.
6.3.
Метод
стандартных
переходных
функций
Как
показано
в
п.
6.2,
расположение
полюсов
системы
определяет
ее
показатели
качества.
С
другой
стороны,
по
заданным
качественным
показателям
можно
найти
область
расположеНI:iЯ
полюсов
и
затем
осуществить
синтез
системы,
обеспечива
ющей
требуемое
качество
процессов
(см.
п.
7.3).
Непосредственное
решение
задачи
нахождения
полюсов
по
заданным
показателям
переходных
характеристик
t
n
и
(1
(см.
п.
6.2)
осуществляется
методом
стандартных
переходных
функций
[4, 20, 29].
Будем рассматривать
устойчивые
системы
вида
где
у*
= 1(t)
У
=
h(t)
4
Система
J-:.
а(р)у
=
Ьу*,
(6.65)
(6.66)
при
нулевых
начальных
условиях
и
постоянном
входном
воздействии
у*
= const, t >
О.
в
этом
случае
установившаяся
составляющая
выходной
переменной
равна
входу
системы:
Уу
=
у*,
а
при
едцничном
входном
воздействии
у*
=
l(t)
выход
y(t)
представлен
переходной
функцией
(см.
2.2.5):
y(t) = h(t)
с
единичной
установившейся
составляющей
уу
=
1.

'-178
Глава
6
..
Качестео
CИC'fем'
управления
к
стандартным
nереходным
функцuям
относят
переходные
процессы,
которые
проходят
в
системе
(6.65)
с
типовыми
характеристическими
полиномами:
полино
мом
Баттерворта,
биномом
Ньютона
и
т.
Д.,
И
специальным
расположением
по
люсов
Pi.
Для
таких
систем
известны
достаточно
простые
методы
нахождения
динамических
показателей
качества.
6.3.1.
Полином
Баттерворта
и
переходные
функции
Введем
в
рассмотрение
полином
порядка
2n:
х(р,
-р)
=
р2n
+
(_1)n",-,~n,
где
"'-'о
-
положительное
число.
Корни
х(р,
-р)
на
ходятся
по
формуле
=
"'-'о
2у'(
_1)n+l
2n
(
(2i -
1)7r
..
(2i - 1)7r)
=
"'-'о
СОБ
+ J
sш
,
n . n
(6.67)
Рис.
6.15.
Распределение·
i =
1,2n.
Их
расположение
на
комплексной
плос-
6аперворта
кости
соответствует
распределению
Баттерворта
(рис.
6.15):
корни
размещаются
в
вершинах
правиль
ного
2n-угольника,
и
число
"'-'о
=
'р;
I
определяет
радиус
распределения.
/JалцtlоJl.О-Ч
Баттерворта
(ПБ)
называется
полином
n-го
порядка
а(р),
который
получается
в
результате
факторизации
х(р,
-р)
=
а(р)а(
-р),
и
корни
которого
р;
лежат
в
левой
полуплоскости,
т.
е.
Re
р;
<
О,
i =
~.
Коэффициенты
полинома
можно
найти
из
выражения:
n
а(р)
=
рn
+
аl"'-'орn-l
+ ... +
а
n
_l",-,;;-1
р
+
"'-'~
=
п
(р
-
рп,
(6.68)
i=l
где
значения
р;
заданы
указанным
выше
способом.
Полиномы
1-6-ro
порядков
приведены
в
табл.
6.1.
Нормированные
ПБ
получаются
при
"'-'о
=
1,
им
соответствует
распределение
Бат
терворта
единичного
радиуса
с
корнями
pt:
Iр;1
=
"'-'о
==
1.
Для
таких
полиномов
легко
находятся
переходные
функции
h
1
(t)
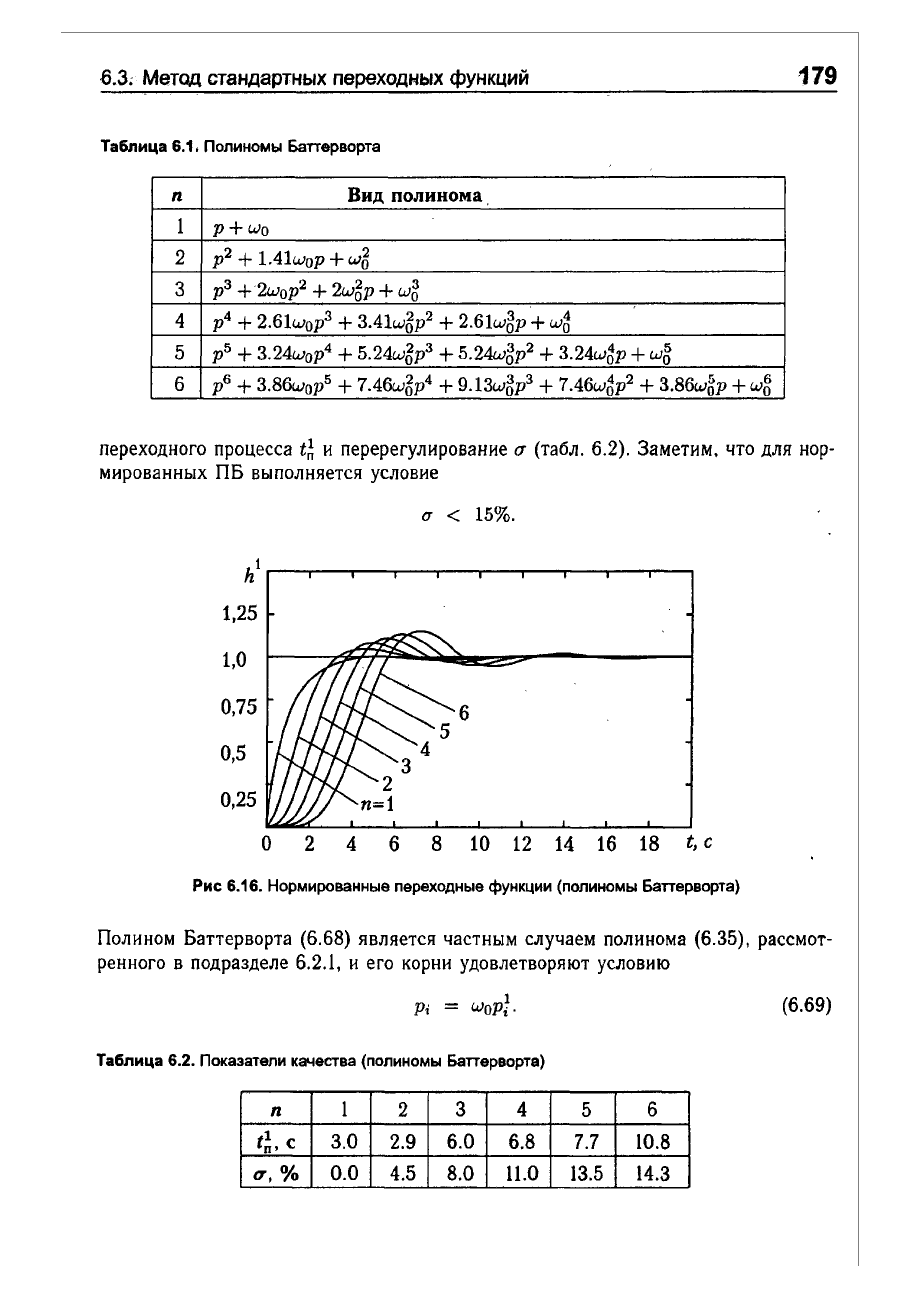
(рис.
6.l6).
По
временным
диаграммам
определяются
динамические
показатели
качества:
время
8.3;
Метод
стандартных
переХОДНЬfХ
функций
179
Таблица
6.1.
Полиномы
Баперворта
n
Вид
полинома.
1
p+wo
2
р2
+ 1.4
1w
op
+
w~
3
р3
+ '
2w
op2
+
2wБР
+
w3
4
р4
+
2.
61w
op3
+
З.41
wбр
2
+ 2.61w3p +
wg
5
р5
+
З.24w
ор
4
+
5.24w~p3
+ 5.24w3
p
2 +
З.24w3р
+
w8
6
р6
+
З.86w
ор
5
+
7.46
wбр
4
+
9.1Зw3
р
3
+ 7.46w3
p
2 +
З.86w8р
+
wg
переходного
процесса
t~
и
перерегулирование
и
(табл.
6.2).
Заметим.
что
для
нор
мированных
ПБ
выполняется
условие
(j
< 15%.
h
1
1,25
1,0
0,75
6
5
0,5
4
3
2
0,25
n=1
О
2 4
6 8
10
12
14
16 18
t,
с
Рис
6.16.
Нормированные
переходные
функции
(полиномы
Баперворта)
Полином
Баттерворта
(6.68)
является
частным
случаем
полинома
(6.35),
рассмот
ренного
в
подразделе
6.2.1,
и
его
корни
удовлетворяют
условию
Pi
= wopf·
(6.69)
Таблица
6.2.
Покаэатели
качества
(полиномы
Баперворта)
n 1
2
3
4
5
6
t~.
с
3.0
2.9
6.0
6.8
7.7
10.8
u,о/о
0.0
4.5 8.0
11.0
13.5
14.3
