Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

50 3 Properties of Dislocations

3.2.4 Interaction Between Parallel Dislocations

The elastic interactions between the moving dislocations and other disloca-

tions in the crystal can basically be understood from the very simple case

of two parallel screw dislocations with equal or opposite Burgers vectors. As

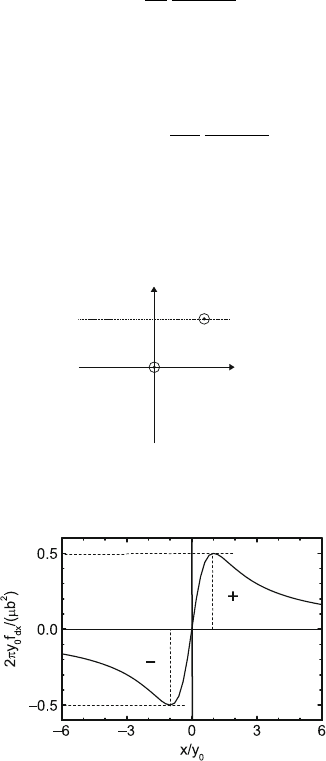
illustrated in Fig. 3.13, one dislocation S1 is situated at the origin of the xy

plane and extends in z direction. It is considered as the source of a ﬁeld of

internal stresses. The other dislocation S2 represents a probe, which is moved

on an xz plane at the distance y

from the origin. Dislocation S1 exerts on S2

a shear stress

μb

2π

+ y

(3.24)

on its xz plane of motion, according to (3.10). Considering (3.20), this stress

causes a Peach–Koehler force in x direction

= σ

b =

μb

2π

+ y

. (3.25)

In Fig. 3.14, the force is plotted as a function of x. It is zero at x =0.

However, there is still σ

= 0, i.e., parallel screw dislocations always attract or

Fig. 3.13. A screw dislocation S2 moving on an xz plane in the stress ﬁeld of

another parallel screw dislocation S1 situated at the origin of the xy plane

Fig. 3.14. Normalized elastic interaction force in x direction experienced by screw

dislocation S2 in the ﬁeld of the screw dislocation S1 of Fig. 3.13

3.2 Elastic Properties of Dislocations 51

repel each other, depending on their respective signs. For the present question

of the glide motion of S2 on the xz plane, only the glide force f

is considered,

no cross slip on other planes. The glide force is positive for positive x values

and Burgers vectors of equal sign, but negative for negative x values. This

means that screw dislocations of equal sign repel each other. For Burgers

vectors of opposite sign, the dislocations attract each other on both sides and

the equilibrium at x = 0 is stable with respect to glide on the xz plane. The

site of the maximum interaction force is found by setting

∂f

∂x

∂σ

∂x

μb

2π

− x

+ y

)

=0.

The solution is x

= ±y

. Putting this into (3.25) yields the maximum force

dxm

= ±

μb

4πy

. (3.26)

If a moving dislocation is to bypass another one, the maximum interac-

tion force has to be overcome by applying an external stress, in this case σ

Both the maximum interaction force and the necessary stress to overcome this

force are proportional to 1/y

, i.e., the reciprocal distance between the slip

plane of the gliding dislocation and the dislocation causing the internal stress

ﬁeld. During plastic deformation, the dislocation density increases and, conse-

quently, y

decreases. Thus, to continue plastic deformation, the applied stress

has to increase. This is an essential source of hardening during deformation,

the so-called work-hardening.

For plastic deformation, the behavior of edge dislocations is important,

too. The stress ﬁeld of edge dislocations was introduced in (3.11) and Fig. 3.9.

For the bypassing of two parallel edge dislocations extending in z direction

with Burgers vectors parallel to x and a distance y

between their slip planes,

the stress component σ

in Fig. 3.9c is relevant. Again, one dislocation moves

as a probe in the stress ﬁeld of the other one located at the origin. There are

positions of zero stress for x =0andx = ±y

. For parallel Burgers vectors, the

signs in Fig. 3.9c indicate the directions of the force. For example, near x =0

and x>0 the probe dislocation is pushed to the left, and for x<0tothe

right, i.e., the equilibrium is stable. Table 3.1 presents the stability conditions

of all equilibrium positions for equal and opposite signs of the Burgers vectors.

It shows the stable position for equal signs at x = 0, corresponding to the tilt

grain boundary, and for opposite signs at x = ±y

, corresponding to the edge

dipole. Thus, the edge dislocation dipoles are stable in a position of 45

◦

with

respect to the direction of the Burgers vector.

The maximum force between two bypassing edge dislocations can be

determined in the same way as described earlier for screw dislocations, yielding

μb

8π(1 − ν)y

52 3 Properties of Dislocations

Table 3.1. Equilibrium positions of two edge dislocations with parallel or antipar-

allel Burgers vectors

=0 x

= ±y

= b

Stable, grain boundary Unstable

= −b

Unstable Stable, dislocation dipole

The bypassing (shear) stress is given by τ = f

/b. In other words, an existing

dislocation dipole can be decomposed at a certain stress if its height h is

greater than a critical height

μb

8π(1 − ν)τ

. (3.27)

This is the so-called dipole opening criterion.

If dislocations capture each other in the described equilibrium conﬁgura-

tions, the total defect energy is reduced since the stress ﬁelds annihilate far

from the dipole. A reference measure is the energy of a dislocation with an

outer cut-oﬀ radius R in the logarithmic term of (3.15) equal to the aver-

age distance between the dislocations. For a screw dislocation dipole, R in

(3.13) has to be set equal to the mutual distance between the dislocations

[85]. Since the distance between the dislocations in the dipole is mostly much

smaller than the average distance between the dislocations, the energy of the

dipole is remarkably lower than the above reference energy. Such a disloca-

tion structure where the long-range stresses partially cancel each other may

be called a low-energy dislocation structure (LEDS). If dislocations of equal

sign arrange under stress in nonequilibrium conﬁgurations (dislocation pile-

ups), where their stress ﬁelds amplify each other, the energy is higher than

the reference value. Theories of work-hardening have been developed on the

basis of both concepts [86, 87].

3.2.5 Interaction Between Nonparallel Dislocations

The elastic interaction between nonparallel dislocations is treated in a way

similar to that between parallel ones. One dislocation is considered the origin

of a ﬁeld of internal stresses, and the force on the other probe dislocation

is calculated by the general form of the Peach–Koehler formula (3.22). In

contrast to parallel dislocations, now the force depends on the place along

the dislocation. A very simple case described in detail by Nabarro [85] is that

of two perpendicular straight screw dislocations S1 and S2 with the shortest

distance y

between them as demonstrated in Fig. 3.15. The coordinate x along

the probe dislocation S2 can be described by the angle θ with tan θ = x/y

The glide force (per dislocation length), which is the only force in this case,

is then given by

μb

2πy

cos

θ. (3.28)

3.2 Elastic Properties of Dislocations 53

Fig. 3.15. Force between two orthogonal screw dislocations

A plot of the dependence of the force on the location along S2 is included in

Fig. 3.15. The total force between dislocations of inﬁnite length is obtained

by integrating f

over x from −∞ to +∞ or over θ from −π/2to+π/2,

yielding

μb

. (3.29)

Thus, the total force is independent of the distance y

between the dis-

locations, as ﬁrst noted by Read [88]. However, the force is increasingly

concentrated in the nearest region between both dislocations if the distance

becomes small. In this local region, the force is higher than that between

parallel dislocations of the same distance (3.26).

A number of individual cases is reviewed by Hartley and Hirth [89] and

Bullough and Sharp [90]. For a general treatment, see Hirth and Lothe [12].

In general, the forces have both glide and climb components so that the dis-

locations, if they comply with the forces, may assume complicated curved

shapes. If the sign of the line vector or the Burgers vector of one dislocation is

reversed, the sign of the force reverses, too. If two signs are changed, the sign

of the force does not change. As the maximum force decreases with 1/y

,these

interactions are of long-range character like the interaction between parallel

dislocations.

If moving dislocations meet nonparallel other dislocations, they can inter-

sect each other if the external stress is high enough to overcome the elastic

interaction forces. During the intersection process, kinks or jogs are formed

in both dislocations as outlined in Fig. 3.16, where a screw dislocation S1

is cut by a moving screw dislocation S2. The lattice planes around S1 are

distorted as indicated in Fig. 3.16a. The dislocation line S2 moves along this

distorted plane so that its right part is shifted downward and the left part is

shifted upward. Finally, in Fig. 3.16b, both parts are separated by the amount

of the Burgers vector b

of S1. The connecting part is a jog J

in S2. Like-

wise, the dislocation S1 experiences a shift J

. Whether this is a jog or a kink

depends on the slip plane of S1. The jogs and kinks are subject to the rules

of motion described in Sect. 3.1.2. Thus, the jog J

in S2 cannot glide with

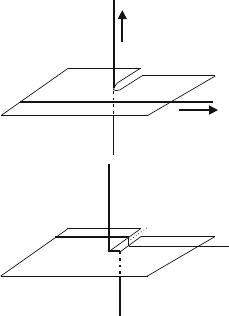
54 3 Properties of Dislocations

(a)

(b)

Fig. 3.16. Mutual intersection between two screw dislocations

the dislocation. It has to climb, which involves diﬀusion, so that the jog acts

as an obstacle to the glide motion of the rest of the dislocation. But even

gliding jogs may represent obstacles since they move on planes diﬀerent from

the main glide plane.

During the intersection process, a piece of additional dislocation line of

the length of the Burgers vector of the cut dislocation is created. Since the

long-range stress ﬁeld of the dislocation is only slightly disturbed, the neces-

sary energy is mainly the core energy, estimated in (3.16). While the elastic

interaction between the cutting dislocations is of long-range character, the

process of formation of the jog is restricted to the neighborhood of the cut-

ting site. It is therefore of short-range nature. Long-range and short-range

interactions behave diﬀerently with respect to thermal activation, as will be

discussed later in Sects. 4.1 and 5.2.

3.2.6 Elastic Interaction Between Dislocations

and Elastic Inclusions

While the foregoing sections treated the mutual interaction between diﬀerent

dislocations, the motion of dislocations is also inﬂuenced by their interac-

tions with other crystal defects, in particular with foreign atoms solved in

the crystals, or with precipitates of second phases. This is the important ﬁeld

of solution and precipitation hardening. To estimate the elastic interaction

forces and energies in the framework of linear elasticity theory, the defects are

considered as elastic inclusions with either a volume which diﬀers from that

of the regular lattice site or with a diﬀerent shear or bulk modulus. Analogous

to the magnetic or electric cases, the interactions are classiﬁed as parelastic or

dielastic ones. Defects with a volume diﬀerence cause a compressive or dilata-

tional elastic stress ﬁeld consisting of pure shear stresses while defects with a

3.2 Elastic Properties of Dislocations 55

diﬀerent shear or bulk modulus do not have an own stress ﬁeld. Instead, they

modify the stress ﬁeld of the interacting dislocation.

The hydrostatic components of the stress ﬁeld of an edge dislocation

produce a pressure

p = −

(σ

+ σ

). (3.30)

Using (3.11) and polar coordinates x = r cos ϕ and y = r sin ϕ, it follows that

p =

μb

sin ϕ

3πr

1+ν

1 − ν

. (3.31)

is the edge component of the Burgers vector. The interaction energy with a

spherical defect of an atomic volume diﬀerence ΔΩ with respect to the volume

Ω of the host lattice site is then given by [91]

ΔW

1 − ν

1+ν

p ΔΩ,

or, if the interaction constant

β =

μb

3π

1+ν

1 − ν

ΔΩ (3.32)

is introduced, it is given by

ΔW

1 − ν

1+ν

sin ϕ

μb

ΔΩ

sin ϕ

. (3.33)

For a dislocation moving on a plane at a certain distance to the elastic

inclusion, the interaction force F

= −∂ΔW

/∂x in the direction of motion x

has a minimum on one side of the inclusion and a maximum on the other.

The signs of these extrema change if the plane of motion changes, e.g., from

the compression side of the dislocation to the tension side. The maximum

parelastic interaction force is given by

≈

μb

ΔΩ

, (3.34)

if the minimum distance between the inclusion and the slip plane is set equal

to half the smallest distance b/

√

6 between the {111} planes in the f.c.c.

structure. This force is remarkably smaller than the interaction force between

nonparallel dislocations (3.29), since |ΔΩ/Ω| is only of the order of magnitude

of 0.1. In many tables, the relative volume diﬀerence ΔΩ/Ω is replaced by the

size misﬁt parameter δ =(1/a)(da/dc), where a is the lattice parameter and

c the concentration of the defects, with δ =ΔΩ/(3Ω). A table of respective

data is given in [92].

The parelastic interaction is of long-range character since it decreases

with 1/r. For mixed dislocations, the edge component of the Burgers vector

56 3 Properties of Dislocations

enters the above equations. Screw dislocations, which do not have a hydro-

static stress ﬁeld, cause only second-order eﬀects. Dielastic interactions aﬀect

both edge and screw dislocations. While the interaction terms are weaker

than for the parelastic interaction, the misﬁt parameters like (1/μ)(dμ/dc)are

greater so that both kinds of interactions may contribute to the hardening.

The models of parelastic and dielastic interactions between dislocations

and spherical inclusions are mainly applied to solution hardening by sub-

stitutional foreign atoms in metals. A strong interaction may arise between

dislocations and defects with a tetragonal stress ﬁeld, as was ﬁrst pointed

out by Fleischer [93]. He calculated the interaction force between a straight

screw dislocation in the cubic structure with a Burgers vector in 110 direc-

tion moving on a slip plane of type {110} (as in the NaCl structure) with

y = const at a distance b to a defect of tetragonal symmetry and 110 dis-

tortion. The dependence of the force F on the position x of the dislocation is

given by

F = F

(x/b)

√

2(x/b) − 1

[(x/b)

+1]

where F

= μΔb

/3.86, and Δ is the diﬀerence between longitudinal and

transverse strains of the tetragonal distortion. For the essential range of x>b,

this function is approximated by the simpler formula [94]

F = F

[(x/b)+1]

−2

, (3.35)

which is frequently called the Fleischer approximation. As this function

describes the dependence of the interaction force on the distance between

the dislocation and the defect along x, it is called a force–distance relation

or an interaction proﬁle. Integrating this function between the applied force

and the maximum force F

yields the interaction energy with the maximum

interaction energy ΔW

= F

b. This can be compared with the maximum

parelastic interaction energy for spherical defects (3.33). With r = b for the

nearest approximation between dislocation and defect, and typical values of

ΔΩ =0.1 b

on one hand and Δ =0.45 on the other, the interaction with

tetragonal defects turns out to be quite strong. In [95], the calculations of

the interaction proﬁle are extended to several orientations of the tetragonal

defects and slip geometries in the NaCl, f.c.c., and b.c.c. structures as well as

to elastic anisotropy. Several cases were recalculated in [96]. The results diﬀer

from the original Fleischer formula. However, the diﬀerences are too small to

be veriﬁed by macroscopic measurements.

The models of the interaction of dislocations and elastic inclusions are

used to interpret the hardening by solutes and small precipitates at low tem-

peratures, where the defects do not diﬀuse, as described in Sect. 4.5. Spherical

inclusions describe the behavior of substitutional defects, while tetragonal

inclusions are applied to interstitial defects, e.g., in b.c.c. crystals and for asso-

ciates between aliovalent impurities and their charge-compensating vacancies

3.2 Elastic Properties of Dislocations 57

in ionic crystals, for which the model was originally derived. At high tem-

peratures, the defects may segregate or, in the case of tetragonal defects,

reorient in the stress ﬁeld of the dislocations. These clouds may be dragged

with the moving dislocations forming a drag stress, which will be described

in Sect. 4.11.

3.2.7 Bowed-Out Dislocations

In the foregoing sections, only straight dislocations were considered. However,

a dislocation segment pinned at its ends will bow out under the action of an

applied stress. The bowing increases the strain energy of the segment because

of the increase in length, ΔW

= EΔL (Sect. 3.2.2). For simplicity, the sub-

script d of E

in (3.15) is dropped here. On the other hand, energy is gained

from sweeping an area ΔA supported by the external resolved shear stress τ,

ΔW

= τbΔA. If the stress is below a critical value, the segment will ﬁnd

an equilibrium position, where ΔW

− ΔW

= 0. The problem of bowed-out

dislocations is mostly treated within the framework of the line tension approx-

imation derived by DeWitt and Koehler [97], analogous to the surface tension

of liquids. In this approximation, the energy of the dislocation depends only

on its orientation β but not on its position with respect to outer or inner

surfaces and to sources of internal stresses like other dislocations, or its own

self-stress, i.e., the logarithmic factor ln(R/r

) in (3.15) is constant.

Figure 3.17 shows a ﬁnite dislocation segment of length L.Onitsleftside,

it is pinned, and it has a hypothetical node A on its right side. Shifting the

node from A to B causes a change of the energy of the segment by a change

in both its length and its orientation β.IfW

= E(β) L is the total energy of

the segment, the change in energy is

= E(β)∂L +

∂E(β)

∂β

L∂β.

To keep the segment in equilibrium, tangential and normal forces have to

act at the end point

= −

∂W

∂L

= −E (3.36)

= −

∂W

∂n

= −

∂W

L∂β

= −E



. (3.37)

∂β

∂L

Fig. 3.17. Shifting the end point of a dislocation segment from A to B

58 3 Properties of Dislocations

E(β)

E'(β)

E'(β)+E"(β)

∂

E(β)+E'(β)

∂

β/2

Fig. 3.18. Force components at the ends of a bent dislocation segment of

inﬁnitesimal length

n is a coordinate in normal direction at the end of the segment with ∂n = L∂β,

and E



is the derivative of E with respect to β. As the line energy tries to

reduce the length of the segment, −E has to act outside to balance the node.

At a bent dislocation segment, these forces are in equilibrium with the Peach–

Koehler force resulting from the external stress, as illustrated in Fig. 3.18. At

the lower end of the segment, E and E



are taken at the orientation angle β,

whereas at the upper end these quantities have to be taken at the angle

β + ∂β. The respective quantities are indicated in the ﬁgure. Since the sign

of the dislocation line vector is opposite at both ends, the sign of the force

vectors is also opposite. The four forces can be projected onto the directions

parallel to the main extension of the dislocation line and perpendicular to it.

The latter projections are marked by the open arrow heads. The components

in direction of the dislocation line cancel each other while the components

perpendicular to it, i.e., in the direction of the dislocation motion, form a net

force pointing at the center of the curved segment. The net force of the two

tangent forces is

(2E + E



∂β)sin

∂β

≈ E∂β.

The net force of the two normal forces is



+ E



∂β −E



)cos

∂β

≈ E



∂β.

Thus, the total force is

∂F

=(E + E



)∂β.

This force is in equilibrium with the Peach–Koehler force (3.20) acting on the

segment owing to the external stress

∂F

= f

∂l = τbr∂β.

3.2 Elastic Properties of Dislocations 59

It follows that the radius of curvature of the segment is given by

r =

E + E



τb

. (3.38)

Γ = E + E



is the line tension. It is a force acting in tangential direction

on a dislocation segment and describing the resistance of the segment against

bowing in the case of a weak bow-out. The line tension approximation is a

method to calculate the radius of curvature of a dislocation segment from the

orientation dependence of the energy of a straight dislocation. With the line

energy in the limit of isotropic elasticity (3.15), the line tension becomes

E =

μb

4π(1 − ν)

(1 − ν cos

β)=E

(1 − ν cos

β)



= E

2 ν(−sin

β +cos

β)

Γ = E

(1 + ν − 3ν sin

β). (3.39)

is the energy of the edge dislocation. The energies and line tensions of the

pure screw and edge dislocations are given in Table 3.2. It follows that the

line tension of the screw dislocation is higher than that of the edge, contrary

to the relation between the line energies. Thus, the stiﬀness against bowing is

higher for the screw dislocation.

For anisotropic crystals, the energy and its second derivative with respect

to the orientation can be calculated within the framework of anisotropic elas-

ticity theory for straight dislocations. In analogy to (3.15), the energy per

dislocation length can then be written as

E = E

(β)ln(R/r

K(β)b

4π

ln (R/r

) , (3.40)

with K =4πE

being the energy factor of the respective dislocation. It

replaces the shear modulus in the respective formulae. In order to calculate



(β), the orientation dependence of E(β) can be represented by a Fourier

series. E



(β) is then obtained by diﬀerentiating the individual terms with

respect to β. Line tension data for a number of f.c.c., b.c.c., and h.c.p. metals

are tabulated in [98].

In order to ﬁnd the equilibrium shape of a long dislocation segment under

stress, a parametric description of the coordinates x and y of the dislocation

can be applied [97]

Table 3.2. Line energy and line tension of screw and edge dislocations in isotropic

elasticity

Screw Edge

(1 − ν) E

ΓE

(1 + ν) E

(1 − 2ν)