Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

80 4 Dislocation Motion

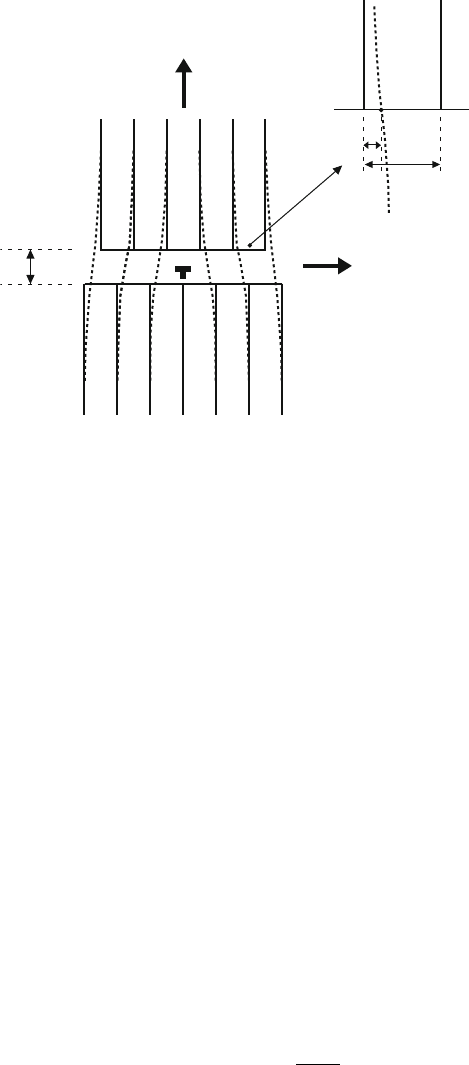
Fig. 4.3. Joining two semi-inﬁnite elastically strained crystals to form an edge

dislocation

by springs and moving on a periodic substrate. At the same time, Orowan

suggested the problem of dislocation motion in a periodic potential relief to

Peierls who solved it in analytical form [127]. Later on it was extended by

Nabarro [128].

In the Peierls–Nabarro model, an edge dislocation is simulated by two

elastic half-crystals, which are shifted with respect to each other by half the

Burgers vector b as outlined in Fig. 4.3 by the two sets of parallel lattice planes.

The half-crystals are positioned at a distance d. To join the lattice planes of the

two half-crystals, these planes have to be displaced on the glide plane in the

middle between the two half-crystals (y =0)by

(x)+b/2forx>0

(x) −b/2forx<0

with respect to the bottom half-crystal. The displaced and joined lattice planes

are represented by dotted lines in Fig. 4.3. Far from the dislocation, the dis-

placements have to fulﬁl the boundary condition u

(∞)=−u

(−∞)=−b/4.

To realize the displacements, internal stresses have to be applied. Similar

to the Frenkel treatment of the theoretical shear strength of Sect. 1.1, it

is assumed that the stresses depend on the displacements via a sinusoidal

function and that the displacements in y direction are comparatively small

(x, 0) = −K sin

4πu

4.2 Lattice Friction 81

K is a constant, which is determined by fulﬁlling Hooke’s law for small strains

μ =

∂σ

∂ε

∂σ

∂u

where ε

(x, 0) = (2u

+ b/2)/(2d). For u

= 0, it follows that

(x, 0) = −

μb

2πd

sin

4πu

. (4.16)

As found out by Eshelby [129], this shear stress distribution can be realized

by a continuous distribution of inﬁnitesimal edge dislocations along the x axis,

leading to an integral equation with the solution

= −

2π

arctan

2x(1 − ν)

. (4.17)

This relation fulﬁls the boundary condition stated above. Besides, u

(d/[2(1−

ν)]) = −b/8=(1/2)u

(∞). Accordingly, in the range −d/[2(1 − ν)] <x<

d/[2(1 −ν)], the disregistry is greater than half its maximum value of −b/4at

x = ∞. This is a possibility to deﬁne a width of the dislocation within which

linear elasticity theory is certainly not valid. The width replaces the core

region of the Volterra dislocation, which is cut out by the inner cut-oﬀ radius.

The method of a continuous distribution of inﬁnitesimal edge dislocations

also allows the calculation of the whole stress ﬁeld of the Peierls dislocation.

The relations reduce to the stress ﬁeld of the Volterra dislocation (3.11) for

distances great with respect to d/[2(1 − ν)]. The Peierls dislocation does not

show the divergence of the stresses in the core of the Volterra dislocation.

The energy of the Peierls dislocation is composed of the elastic energy of

the two half-crystals and the misﬁt energy of the atom rows between them.

For comparing the result with that of the Volterra dislocation, the elastic

energy can be calculated in two half-cylinders, which have to be deformed by

surface forces to yield the displacements u

. Following the original treatments

of Peierls [127] and Nabarro [128], the result is

W (x)=

μb

4π(1 − ν)

μb

2π(1 − ν)

exp −

2πd

b(1 − ν)

cos

4πx

μb

4π(1 − ν)

cos

4πx

. (4.18)

is called the Peierls energy and represents the magnitude of the periodic

displacement potential. The dislocation energy varies with double the lattice

periodicity b because of the two symmetrical positions in Fig. 4.2. However,

(4.18) does not correspond to the expectation from Fig. 4.2 as the symmetrical

positions turn out to be positions of maximum energy. This result originates

from the method of summing up the energies of the individual lattice rows in

the two original treatments. The method was improved by Hirth and Lothe

82 4 Dislocation Motion

[130] omitting this problem. The maximum of the derivative of W (x)with

respect to the position x of the dislocation yields the stress necessary to move

the dislocation over the potential barrier



∂W(x)

∂x



max

2πW

2μ

1 − ν

exp −

2πd

b(1 − ν)

. (4.19)

This is the Peierls–Nabarro stress or shortly Peierls stress to move a

straight dislocation lying in a Peierls valley only by mechanical stress, that

is, at very low temperatures. For d ≈ b, it is in the range of 10

−4

...10

−2

μ,

that means in the range of the real shear strengths of materials. The lattice

resistance is controlled by the structure of the dislocation cores. Therefore,

the Peierls–Nabarro model is too coarse for detailed predictions of the ﬂow

stress of crystals. Similar to the theoretical yield stress of perfect crystals in

Sect. 1.1, the Peierls stress is small for small Burgers vectors b and large dis-

tances d between the lattice planes. According to the experimental results,

the Peierls stress is small for close-packed structures like f.c.c. metals, where

it does not play a role except at low temperatures. It is high for materials

with directional bonds like the covalent semiconductor and ceramic crystals,

which become plastic only at high temperatures. The b.c.c. metals show an

intermediate behavior.

The Peierls–Nabarro model is reﬁned in many ways: by relaxing the severe

assumptions made and by using more realistic potentials than the sinusoidal

one (e.g. [131]). More detailed information on the dislocation core conﬁgura-

tions and energies as well as the Peierls stress can be obtained from atomistic

calculations. The crystal is divided into an outer zone, which is treated by

continuum elasticity theory and a core region where the interactions between

the atoms are calculated discretely. The positions that are ﬁrst determined by

the elastic solution are then varied to ﬁnd the equilibrium conﬁgurations. The

results of these calculations depend very sensitively on the chosen interaction

potentials between the atoms. The situation is comparatively simple in ionic

crystals with Coulomb attraction, Born–Mayer repulsion, and van-der-Waals

potentials. Early calculations of this kind were made in [132] for NaCl and

in [133] for MgO. For metallic materials, the semi-empirical embedded-atom

method (EAM) is quite successful (for a review see [134]). In recent studies

of dislocation cores and the Peierls stress, details of the dislocation behavior

were interpreted, for example, for intermetallic alloys [135] or on the inﬂuence

of shear stresses in more than one slip plane and of nonglide stresses in b.c.c.

Mo [136]. In a model cubic primitive lattice, the Peierls stress was calculated

by molecular dynamics simulation [137]. Applying a sinusoidal interaction

between the atoms, the Peierls potential also turns out to be close to sinu-

soidal, as assumed in most continuum models. As a general result of the

atomistic calculations, it may be stated that the eﬀective core radius intro-

duced in Sect. 3.2.2, which is chosen to include the core energy within the

elastic solution, is slightly less than 0.5b in ionic crystals, and 0.5b toafewb

in metals.

4.2 Lattice Friction 83

Hirth and Lothe [12] suggest to use a phenomenological equation for the

Peierls potential

W (x)=



1 − cos

2πx



= W

sin

πx

, (4.20)

where h either equals b/2orb, depending on the degree of equivalence of the

two equilibrium conﬁgurations. Accordingly, the Peierls stress becomes

πW

. (4.21)

4.2.2 Double-Kink Model

In the same way in which the high energy necessary to shear two lattice planes

with respect to each other as a whole is expended in small steps by the motion

of a straight dislocation from one Peierls valley to the next, this shift can

again be performed in small steps by the generation and sidewise spreading

of kinks. At low stresses, the kinks may occur in their thermal equilibrium

concentration. At higher stresses, they form under the action of the stress. For

dislocations not lying in a Peierls valley, that is, not being parallel to a low-

index crystallographic direction, kinks are necessary for geometric reasons. As

shown in Fig. 4.4a, kinks may appear as single kinks K or kink pairs K

−

Depending on the binding properties of the material, the kinks can be abrupt

as in Fig. 4.4a or may have a deﬁned width w as in Fig. 4.4b. If the kinks

are treated within the framework of the line tension model, the dislocation

changes in a smooth way from one Peierls valley to the next (Fig. 4.4c). The

sidewise motion of the kinks along the dislocation as indicated by the arrows

in Fig. 4.4c shifts the dislocation forward (upwards) in small steps.

Elastic Properties of Kinks

The properties of the kink formation depend on their energy, which can be

estimated from continuum elasticity theory. Kink pairs or double-kinks of

height h can be formed by putting a segment of length L of a straight dislo-

cation into the neighboring Peierls valley. For kinks of small h with respect to

L, the energy of the kink pair is given by

fdk

=2W

+ W

int

, (4.22)

where W

is the formation energy of a single kink and W

int

is the interac-

tion energy between both kinks. Using the conﬁguration of Fig. 4.4a of sharp

kinks, the kink formation energy can be determined for kinks of height h

large compared to the inner cut-oﬀ radius r

. This condition is not fulﬁlled

for elementary kinks. Since the long-range stress ﬁeld of a dislocation is not

disturbed remarkably by introducing a kink, the core energy of (3.16) of a

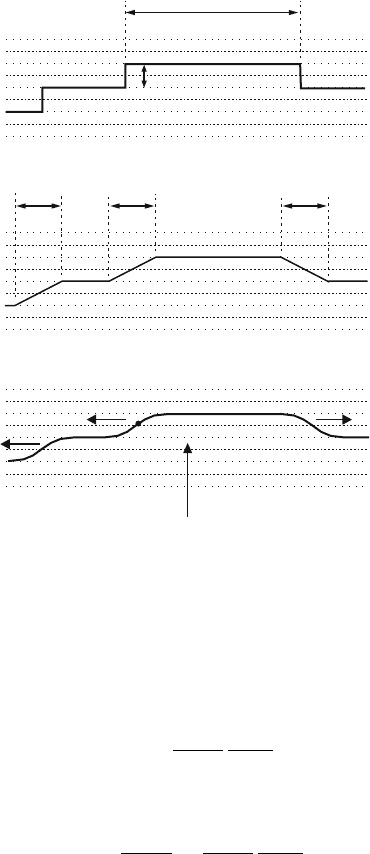
84 4 Dislocation Motion

ww w

(b)

(c)

(a)

Fig. 4.4. Conﬁgurations of single kinks K and kink pairs K

−

.(a) Abrupt kinks.

(b)Kinksofwidthw.(c) Smooth kinks. Dotted lines: Peierls valleys, dashed lines:

Peierls hills

piece of dislocation of length h can be taken for the kink formation energy,

≈ (1/10)μb

h. This problem does not occur for the interaction energy.

For a kink pair in a screw dislocation, it is given by

int

= −

μb

8πL

1+ν

1 − ν

. (4.23)

There follows the attractive interaction force

int

∂W

int

∂L

μb

8πL

1+ν

1 − ν

. (4.24)

This expression can be veriﬁed by applying Brown’s theorem (3.44). The

same equation holds for the extended kink conﬁguration in Fig. 4.4b as long

as L>w. For a kink pair in an edge dislocation, the factor 1 + ν has to

be replaced by 1 − 2ν (see Table 3.2 for the line tensions of screw and edge

dislocations). It should be noted that the interaction force decreases quickly

with 1/L

in contrast to long dislocations where the interaction force decreases

with the reciprocal distance (e.g. Sect. 3.2.4). The calculation of the energy

4.2 Lattice Friction 85

of individual kinks is more complicated as they have to form at a surface so

that image terms have to be considered.

The kink energy can also be determined using the line tension model in its

simple version of constant line tension equal to the line energy E

, for instance

(3.17). The dislocation is assumed to have the smooth kink conﬁguration

of Fig. 4.4c. At some point P of the kink, the line tension acts as a force

in tangential direction of the dislocation line. This force has a component

in forward x direction. It is balanced at any point along the kink by the

force ∂W(x)/∂x resulting from the Peierls potential, taken, for example, from

(4.20), and by the force from the applied stress τ

∗

. Thus, the equilibrium

condition is [138]

= −E

− τ

∗

b =0. (4.25)

The solution of the problem for zero stress yields



. (4.26)

This formula, which expresses the kink formation energy in terms of the

Peierls energy and the dislocation line energy, links the Peierls–Nabarro model

for the motion of a straight dislocation at low temperature, that is, a quantity

describing the periodic lattice potential, with the double-kink model of realis-

tic dislocation motion. For the formation of the kinks at constant temperature,

the free energy of kink formation ΔF

has to be used instead of the energy.

However, the uncertainties of the elastic estimates above are greater than the

entropy contribution so that ΔF

≈ W

. Like the dislocation energy W (x)in

(4.18),thekinkenergy,too,showsalattice periodicity resulting in an energy

barrier to the motion of kinks. The respective potential is sometimes called

the Peierls potential of second order.

Kinks in Thermal Equilibrium

At a ﬁnite temperature, the equilibrium conﬁguration of a dislocation is not

a straight line lying in a Peierls valley but a dislocation containing a certain

concentration of kinks. Inside the crystal, the kinks can only be formed as kink

pairs with equal numbers of positive and negative kinks and a well-deﬁned free

energy of formation 2ΔF

of the kink pairs. Their concentration is governed

by a minimum in the free energy of the system, that is,

∂ΔF

∂n

=0, (4.27)

if n is the number of kinks of one sign along a dislocation of length L.Each

kink increases the free energy of the system by ΔF

, yielding the total increase

nΔF

86 4 Dislocation Motion

On the other hand, a conﬁgurational entropy occurs

ΔS = k ln P

where P

is the number of possibilities to arrange the n kinks of one sign

at the respective number of possible kink sites N = L/a inside L.Fora

single kink, P

= N.Fortwokinks,P

N(N − 1). For three kinks, P

N(N − 1)(N − 2). The factors 1/2, 1/6, etc. consider that the individual

kinks cannot be distinguished from each other. Thus, for n kinks of one sign

N(N − 1) ...(N − n +1)=

(N − n)!n!

. (4.28)

For the change in the free energy by introducing n kink pairs, this yields

ΔF =2(nΔF

− kT ln P

) .

Inserting (4.28) and using Stirling’s formula for large n,

ln x!=x ln x − x

yields

∂ΔF

∂n

=ΔF

− kT ln

N − n

for the equilibrium condition (4.27). Introducing the kink concentrations of

positive and negative kinks c

= c

−

= n/L and considering that n  N

ﬁnally results in an equilibrium concentration of kinks

= c

−

exp



−

ΔF



. (4.29)

This derivation is typical also for a number of other processes where defects

exist in thermal equilibrium. A very prominent case, which will be discussed in

Sect. 4.10, is the occurrence of thermal point defects, vacancies, and interstitial

atoms.

Thermally Activated Motion of Kinks

The kink formation energy, which frequently is of the order of magnitude of

the dislocation core energy, is not very high, for simple metals it is only a

fraction of one electron-volt. The kink migration energy is due to the periodic

variation of the kink energy. This variation is sometimes called the secondary

Peierls potential. It is mostly small so that the kink motion can be aided

by thermal activation. Since the height of the elementary kinks is also small

(in the order of b), the force acting from the applied stress is small, too.

Therefore, the kink motion can be treated by the theory of diﬀusion. For a

4.2 Lattice Friction 87

general introduction into diﬀusion see [139, 140]. The diﬀusion coeﬃcient for

the diﬀusion of kinks along the dislocation line is deﬁned by

= a

ω, (4.30)

where a is the jump distance of the kink and ω the jump frequency. When

asmallforceF acts on the kink, the jump frequency in forward direction

becomes higher than that in backward direction, resulting in a drift velocity,

which is given by the Einstein relation

F. (4.31)

In general, the force F can originate from a mechanical stress, but as

thermodynamic force also from a chemical potential μ = kT ln(c/c

), where

c is the concentration of some species and c

its equilibrium value. The force

is then

F = −

∂μ

∂x

= −

∂c

∂x

. (4.32)

Equations (4.31) and (4.32) together yield Fick’s ﬁrst law

J = cv

= −D

∂c

∂x

. (4.33)

Here, J is the ﬂux or current density. The frequency ω to move a kink over

the activation barrier is given by

ω ≈ ν

exp



−

ΔF



. (4.34)

In this case, the attempt frequency ν

is approximately equal to the Debye

frequency ν

=10

...10

−1

.ΔF

is the free energy of kink migration.

For kink motion, the force in (4.31) results from a shear stress τ acting on the

slip system of the dislocation, that is,

F = τbh.

Correctly speaking, τ is the locally acting stress. The superscript * is dropped

in the following considerations. Together with (4.30), (4.31), and (4.34), this

relation yields the velocity of the kink along the dislocation

= D

τbh

≈ ν

exp



−

ΔF



τbh

. (4.35)

Except in crystals with strong directional bonds, the kink migration energy

is quite small and much smaller than the kink formation energy. Therefore,

kinks often move very fast so that their velocity is controlled by high speed

damping processes, which will brieﬂy be described in Sect. 4.12. Under certain

88 4 Dislocation Motion

conditions, the diﬀusion coeﬃcient of kinks is then constant, approximately

equal to the limiting case of ΔF

 kT , but this coincidence is fortuitous.

To conclude the dislocation velocity v

from the kink velocity, the concen-

tration of kinks c

must be known

= hc

. (4.36)

There are diﬀerent situations depending on the magnitude of the force acting

on the kinks, or on the applied stress. For small stresses, the kink concentra-

tion does not diﬀer remarkably from the thermal equilibrium concentration

in (4.29). For high stresses, kink pairs are formed by stress-assisted thermal

activation so that the concentration of kinks is much higher than in the small

stress regime. In the latter case, (4.29) and (4.35) can be inserted into (4.36).

Considering further that c

= c

+ c

−

yields an expression for the dislocation

velocity in the small stress region,

2τbh

akT

exp



−

ΔF



. (4.37)

Double-Kink Nucleation at High Stresses

At high stresses, kink pairs are formed by stress-assisted thermal activation.

Only kink pairs moving the dislocation forward, which are favored by the

applied stress, need to be considered as kink pairs moving the dislocation

backwards will immediately shrink and annihilate. Because of the mutual

elastic interaction energy of the kinks of the pair (4.23), which decreases with

increasing kink separation L, and the increasing energy gained from the exter-

nal stress, the formation energy of a double-kink ΔF

fdk

will show a maximum

at a critical separation L

∗

of the kinks, as schematically shown in Fig. 4.5. At

the critical separation, the attractive kink interaction force is balanced by the

force τbh due to the external stress, which drives the kinks apart. Kink pairs

with separations smaller than L

∗

collapse with a gain in energy. Those with

L>L

∗

tend to separate further. However, kink pairs close to L

∗

can still

annihilate so that only those which are wider than L



are really stable. The

energy diﬀerence between the states at L

∗

and L



is in the order of magni-

tude of kT. This behavior of the free energy of double-kink formation and the

related nucleation and annihilation properties very much resemble the steady

state nucleation theory [141–145] as it was developed, for example, for crystal

growth [146]. With some approximations, the result of this theory yields the

double-kink nucleation rate

τbh

exp



−

ΔF

∗

fdk



. (4.38)

ΔF

∗

fdk

is the maximum value of the double-kink formation energy at the crit-

ical separation L

∗

. To obtain the dependence of the double-kink formation

4.2 Lattice Friction 89

Fig. 4.5. Schematic plot of the dependence of the double-kink formation energy on

the separation of the kinks. Dashed line: without external stress. Solid line:with

external stress. See text below

energy ΔF

fdk

(L) on the kink separation as depicted in Fig. 4.5, both the contri-

bution of the kink interaction energy (4.23) introduced by Seeger and Schiller

[147, 148] and the work done by the external stress have to be considered.

With average data of screw and edge dislocations, the formation free energy

for kink pairs of a separation larger than the kink width w canbewrittenas

ΔF

fdk

(L)=2ΔF

−

μb

8πL

− τbhL. (4.39)

The critical separation L

∗

of the kink pairs can be obtained by



∂ΔF

fdk

∂L



L=L

∗

=0,

yielding

∗



μbh

8πτ

Inserting this into (4.39) results in the critical double-kink formation energy

ΔF

∗

fdk

=2ΔF

−



μτb

2π

. (4.40)

Evaluations of experimental data are often based on this formula, c.f. [149].

For a relatively low stress of τ =10

−4

μ and h = b, the critical kink separation

is L

∗

=20b. Thus, the kinks are well separated. Using (4.19) and (4.26), a

Peierls stress of τ

=10

−2

μ, and a dislocation energy of E

= μb

/2 (3.17),

the formation energy of two separated kinks becomes 2ΔF

=10

√

μ/π

3/2

Considering that μb

=5eV,2ΔF

≈ 0.25 eV. Compared to this value, the

last term in (4.40) amounts to only 10% of the total energy. Thus, for this