Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

110 4 Dislocation Motion

It was shown by Schoeck [207] that the linear superposition rule of the stress

contributions holds for low temperatures. At high temperatures, however, the

waiting times at the weak obstacles are very short so that only the strong

obstacles control the ﬂow stress. Computer simulation studies [208] of the

thermally activated motion through an array of obstacles of very diﬀerent

strengths suggest that under most conditions the dislocation motion is jerky

as shown in Fig. 4.18, that the strain rate sensitivity is controlled by the

strong obstacles and is exclusively controlled by τ



/τ



The transition from a regular arrangement of obstacles to a random one

was treated in [209]. The ﬂow stress decreases rapidly already for small

deviations from regularity.

In summary:

• The macroscopic properties of dislocation motion in an array of localized

obstacles obeying Friedel statistics are well described by the Friedel length

(4.53) or, in normalized form, (4.54).

• The relation between the athermal ﬂow stress and the obstacle strength is

obtained by replacing the square lattice distance in a regular arrangement

of the obstacles by the Friedel length (4.56) or, in normalized form, (4.57).

• The same relation holds also for thermal activation. However, instead of

the obstacle strength, the force where the force distribution breaks oﬀ has

to be used.

• The distribution of the obstacle distances and its mean value are a mea-

sure of the density of localized obstacles actually impeding the dislocation

motion.

• The kinematic character of the dislocation motion allows conclusions to

be drawn on the relation between the actual stress and the athermal ﬂow

stress of the obstacle array. At low relative stresses, the dislocation motion

is jerky on the scale of the square lattice distance, and the obstacles are

surmounted with the aid of thermal activation. At high relative stresses,

the dislocations move very jerkily on the scale of several hundreds of the

square lattice distance.

The range of application of Friedel statistics is hardening by solute atoms

and small precipitates of low concentration but high strength. Experimen-

tal data on the microscopic aspects of dislocations overcoming localized

obstacles will be described in the sections on ceramic crystals and metallic

alloys in Part II. Details of the dislocation conﬁgurations and the kinematic

behavior of dislocations from in situ straining experiments will be given in

Sect. 7.2.

4.5.2 Mott Statistics

If ξ

in (4.52) is not small with respect to unity, the extensions of the obstacles

cannot be neglected and Friedel statistics is not valid. This holds in particular

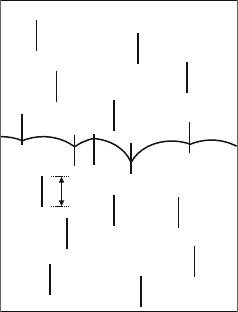
4.5 Overcoming of Localized Obstacles 111

Fig. 4.19. A dislocation interacting with localized obstacles of width ξ

in x

direction which obey Mott statistics

for weak obstacles with small f

. Applying a suitable transformation, Schwarz

and Labusch [187] show that the width in z direction along the dislocation

line can be neglected for weak obstacles so that they act like ribbons extended

only in x direction, as demonstrated in Fig. 4.19.

Schwarz and Labusch treat the problem by establishing the diﬀeren-

tial equation of the motion of the dislocation (see Sect. 4.9) in the ﬁeld of

obstacles in the approximation of constant line tension. For the interaction

proﬁle between the dislocation and a single obstacle, a force–distance curve

according to

f(ξ)=A

(ξ/ξ

)(1− (ξ/ξ

)

is used in the interval −1 ≤ (ξ/ξ

) ≤ 1. This interaction proﬁle includes a

repulsive and an attractive branch. The results are almost independent of the

exponent n. For the simulation of thermal activation described below, n =2

was used. The constant A

is chosen as to obtain f

= 1. The equation of

motion contains also a damping term. For the athermal case, it was solved by

numerical simulation. For ξ

< 0.8andn = 2, the athermal ﬂow stress is



3/2

(1 + 0.55ξ

conﬁrming the result of Friedel statistics (4.57) for ξ

= 0. The constant k

also almost equal to the value quoted above. For 0.8 <ξ

≤ 4, the simulation

results suggest



3/2

(1 + 2.5ξ

)

1/3

. (4.65)

Thus, the athermal ﬂow stress depends on the width of the obstacles.

It is higher than that for Friedel statistics. The motion of the dislocation

supported by thermal activation is simulated by adding random point forces

to the equation of motion [210]. The results of the simulations are summarized

in empirical relations. All Arrhenius plots meet a reasonable straight line of

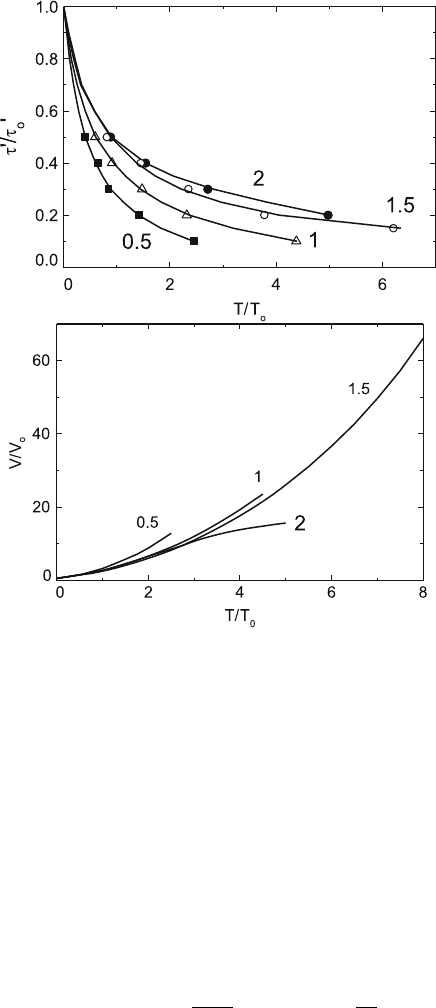
112 4 Dislocation Motion

Fig. 4.20. Results of the computer simulations in [210] of dislocations moving

through obstacles extended in the x direction. (a) Dependence of the relative stress



/τ



on the relative temperature T/T

. The parameter is ξ

.(b) Dependence of the

eﬀective activation volume normalized by V

= gξ

on the relative temperature

the slope −1iflnv

is plotted vs. a quantity F

(τ



,ξ

)ΔE

/(kT). Here, v

is the dislocation velocity, F

a scaling factor depending on the stress and

the width of the obstacles, and ΔE

= gF

is the activation energy at

zero force for overcoming the individual obstacles. g is a geometrical factor

close to unity depending on the shape of the interaction proﬁle. The scaling

factor F

represents the ratio between an eﬀective activation energy ΔE

eﬀ

and the activation energy ΔE

to overcome the individual obstacles. Using

the modiﬁed Arrhenius equation (4.7) for a constant dislocation velocity v

exp(−F

ΔE

/(kT)), one can write

(τ



/τ



,ξ

ΔE

ln(v

with T

=ΔE

/(k ln(v

)). Inversion of this relation yields the relative

ﬂow stress τ



/τ



as a function of the temperature with ξ

as a parameter. This

4.6 Transition from Double-Kink to Obstacle Mechanism 113

is plotted in Fig. 4.20a. Thus, the ﬂow stress normalized by the athermal ﬂow

stress decreases very slowly with increasing temperature, the more slowly the

larger is ξ

. For point obstacles, the ﬂow stress contribution is already small

at T

The other quantity that can be compared with experimental results is the

activation volume

V = −

∂ΔE

eﬀ

∂τ

= −

ΔE

∂(ΔE

eﬀ

/ΔE

)

∂τ



Using the Friedel relation (4.56) for τ

shows that the ﬁrst factor in the

equation becomes V

=ΔE

/τ

= gξ

. The second factor V/V

is obtained

numerically from Fig. 4.20a, and it is plotted in Fig. 4.20b. In the Friedel case,

the activation volume is of the order of b

. In the Mott–Labusch situation,

even V

is greater than that as g and ξ

are close to unity but l

is greater

than b. In addition, Fig. 4.20b indicates activation volumes being larger than

by a factor of several tens.

In conclusion, the theory of Labusch and Schwarz shows that for weak

obstacles extended in the x direction of forward motion

• The athermal ﬂow stress depends on the normalized obstacle width.

• The obstacles are not overcome individually by thermal activation but

collectively in groups.

• As a consequence, the eﬀective activation energy and the activation volume

are far greater than the values for overcoming the single obstacles.

• The obstacles contribute to the ﬂow stress at high temperatures where

individual obstacles are no longer active.

Mott–Labusch statistics is applied to solution hardening, especially of sub-

stitutional alloys with a high concentration of weak obstacles. In addition to

a relatively steep low-temperature increase, the model explains the plateau-

like weak decrease of the ﬂow stress at higher temperatures. In Sect. 9.4, the

model will be applied to NiAl containing 0.5 at% Ti.

4.6 Transition from the Double-Kink Mechanism

to the Overcoming of Localized Obstacles

The activation parameters of the double-kink (Peierls) model and the models

of overcoming localized obstacles are quite diﬀerent so that these mechanisms

act in diﬀerent ranges of temperature and dislocation velocity or strain rate.

In the transition region, both mechanisms act simultaneously and the net dis-

location velocity is controlled by both the waiting time t

of the dislocation

pinned at the obstacles, (4.3) and (4.6), and the traveling time t

between the

stable conﬁgurations determined by the double-kink mechanism. In the lim-

iting case of localized obstacles acting alone, the traveling time is neglected,

114 4 Dislocation Motion

τ*

ΔG

Fig. 4.21. Schematic plot of the dependence of the Gibbs free energy of activation on

the eﬀective stress for overcoming localized obstacles and the double-kink mechanism

 t

. If only the Peierls mechanism acts, t

 t

. In a simpliﬁed treatment

where the diﬀerence in the pre-exponential factors is neglected, the transition

between both mechanisms occurs when the respective Gibbs free energies of

activation are equal, as outlined in Fig. 4.21. At high temperatures correspond-

ing to low stresses, where localized obstacles control the deformation, ΔG

large. The activation volume V is large, too, as it contains the obstacle dis-

tance l or multiples of it. This leads to a strong dependence of the activation

energy ΔG

on the eﬀective stress τ

∗

. The double-kink mechanism has a low

activation energy ΔG

≈ ΔF

+ΔF

or ≈ ΔF

+2ΔF

, (4.46) or (4.47),

and a small activation volume resulting in a very weak dependence of ΔG

on τ

∗

. Both curves intersect at the transition stress τ

∗

or the corresponding

transition temperature.

In a more detailed picture, it turns out that both mechanisms inﬂuence

each other. A theory of dislocation motion in the combined relief of the

extended Peierls barriers and localized obstacles was developed in [211]. If the

Peierls mechanism is neglected, the dislocation segments bowing out under

stress acquire only a single equilibrium conﬁguration, which can be described,

for example, by the line tension approximation. In the more general case of

the combined action of the double-kink mechanism and localized obstacles,

owing to the periodic Peierls potential, many locally stable or metastable con-

ﬁgurations appear, which can be characterized by their bowing heights h in

the center of the segments. Diﬀerent positions are shown in Fig. 4.22.

The equilibrium states are revealed in the line tension approximation by

minimizing the energy of a curved dislocation in the ﬁeld of the Peierls poten-

tial as discussed already in (4.25). For the segments pinned at their ends at

z =0,x= h; z = ±l/2l, x = 0 the integration yields [212]

E =2





2Γ [W

(x) −W

(h)+τ

∗

b(h − x)] dx +[W

(h) − τ

∗

bh] l.

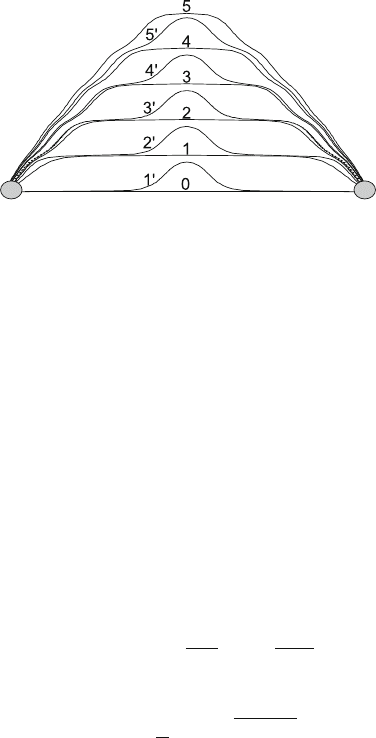
4.6 Transition from Double-Kink to Obstacle Mechanism 115

Fig. 4.22. Stable and metastable conﬁgurations of a dislocation segment bowing out

between localized obstacles under the simultaneous action of the Peierls mechanism.

From [212]. Copyright EDP Sciences (2000)

The solutions of the problem are presented in Fig. 4.22. The conﬁgurations

with an extended ﬂat top designated by numbers n are stable solutions,

whereas the solutions withatipdesignatedbyn



are unstable and corre-

spond to ordinary kink pairs on a straight dislocation. In the intermediate

stable positions, the angles of attack at the obstacles are larger than in the

limiting conﬁguration without the Peierls mechanism. Correspondingly, the

forces on the obstacles are smaller. To study the kinematics of the dislocation

motion, the activation energies for the transitions between the stable posi-

tions have to be calculated. For small bowing, i.e., for dislocation segments

with an extended straight top, the activation energy corresponds to the usual

double-kink mechanism, which can be approximated for the harmonic Peierls

potential (4.20) by

ΔG

(τ

∗

) ≈ 2ΔF



1 −

πτ

∗

8τ



16τ

πτ

∗





, (4.66)

where

ΔF





3/2



Γτ

The stress dependence of the activation energy with both the Peierls poten-

tial and localized obstacles being present is characterized by several branches

corresponding to the numbers n of the diﬀerent Peierls valleys. For high

stresses, all these branches form the curve of the usual Peierls mechanism

(4.66). However, with decreasing stress, the curves of the diﬀerent conﬁgura-

tions n reach a limiting stress where the activation energy strongly increases.

Below this limiting stress, there does not exist an equilibrium conﬁguration

with the respective n value. These abnormal increases of the respective acti-

vation energies result in either a strong increase in the activation volume with

respect to the usual Peierls mechanism at low stresses τ

∗

< 0.1 τ

,orinavery

steep decrease of the strain rate sensitivity during the transition between the

action of the Peierls mechanism at low temperatures and localized obstacles

at higher ones, as shown in Fig. 4.23 in comparison with experimental data

116 4 Dislocation Motion

Fig. 4.23. Strain rate sensitivity of cubic ZrO

as a function of temperature.

Experimental data from [213] (open squares) and from deformation under conﬁn-

ing hydrostatic pressure [214] (upright and tilted crosses). Theoretical curve below

transition temperature after transition model (full line 1 ) and after simple theory

(dashed line 2 ). Theoretical curve above transition temperature for precipitation

hardening, see Sect. 7.3.5. Data from [212]

from ZrO

single crystals. The properties of this material are described in

more detail in Sect. 7.3.

If the double-kink mechanism acts, localized obstacles cannot only impede

the dislocation motion, but they can also advance it by facilitating double-kink

nucleation, thus leading to softening. For a recent review, see [215].

4.7 Overcoming of Extended Obstacles

Large precipitates can frequently not be treated by the model of localized

obstacles which extend only in forward (x) direction of the dislocation motion.

Kocks et al. [9] described the interaction between penetrable particles with

dislocations in a simple line tension model. Impenetrable obstacles can be

passed only by forming a dislocation loop around the obstacle. This process

will be described below.

The following line tension model is restricted to isotropic line tension,

where the dislocation segments bow out to form circular arcs. It can also be

extended to anisotropic line tension. The resisting forces of the particles are in

equilibrium with the line tension forces of the bowed-out dislocation segments

between the particles. The balance is attained at the border line of the cutting

face of the obstacles as will be discussed later. The model allows a uniﬁed

description of the diﬀerent resistance mechanisms and the calculation of the

force–distance proﬁle of extended obstacles. These may cause the following

resistance eﬀects on the dislocations.

4.7 Overcoming of Extended Obstacles 117

1. Friction stresses in the interior of the particles. They result from all mech-

anisms requiring energy to be spent being proportional to the area swept

by the dislocation like the formation of an antiphase boundary in inter-

metallic alloys (Sect. 3.3.4). The friction stress is given by τ

= γ/b,where

γ is the fault energy per area. The resistance eﬀect can be represented by

the dislocation being bowed-out inside the particle in backward direction

[216]. The radius of curvature is deﬁned by (3.38) with the line tension

equal to the line energy Γ = E

for the isotropic line tension

b (τ

− τ

∗

)

. (4.67)

The index p indicates that these quantities are related to the interior of

the particle. The stress that determines the curvature in the particle is

the diﬀerence between the friction stress τ

and the local eﬀective stress

∗

, which supports the dislocation motion also inside the particle.

2. Forces acting at the border line of the particles. Their displacement along

the border line may create, for example, the energy necessary to form

additional interface area at the surface steps trailed by the dislocations.

The forces may be taken into account by their components parallel to the

edge and screw directions of the dislocations. They cause a knee in the

dislocation line at the particle border.

3. Diﬀerent line energies in the particle and the matrix, for example, owing to

diﬀerent elastic constants. This eﬀect also causes a knee in the dislocation

line.

During the forward motion of the dislocation, the contact point between

the dislocation and the particle moves along the border line. According to

[9, 216], the components of the acting forces and the line tension forces along

the tangent to the particle border always have to be in equilibrium, as outlined

in Fig. 4.24. The ﬁgure shows part of the cutting plane of a particle with

the border B. The dislocation line L extends outside and inside the particle. At

the intersection between the dislocation and the border line, the tangent to the

border has the angle θ with respect to the x coordinate. The dislocation has

the tangent angle ψ inside the particle and φ outside of it. At the intersection

point, the forces K

and K

act on the dislocation. Only K

is plotted in

the ﬁgure. In addition, line tensions (or energies) E

act in the particle and

in the matrix. At the intersection point, the line tensions act as forces in

tangential directions. A variational procedure shows that these forces are in

equilibrium if the sum of their projections onto the tangent direction of the

particle border vanishes [9,216]

cos θ + K

sin θ + E

cos(ψ − θ) − E

cos(φ −θ)=0. (4.68)

The angle φ determines the obstacle force according to (3.48)

F =2E

cos φ. (4.69)

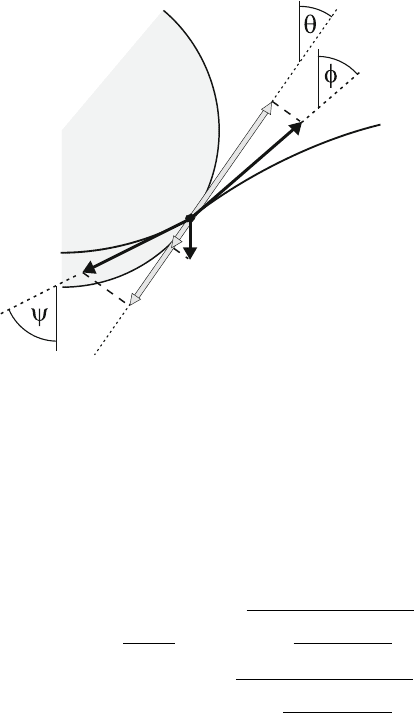
118 4 Dislocation Motion

Fig. 4.24. Force balance along the tangent to the border line of the cutting face of

an extended obstacle

Using cot θ = x



and

cos ψ = zb(τ

− τ

∗

) /E

cos φ =(l/2 − z) bτ

∗

the equilibrium condition (4.68) can be written as



+ K

+ x



bz −



∗

+ E



1 −



zb(τ

− τ

∗

)



−E



1 −



(l/2 − z) bτ

∗



=0. (4.70)

This equation establishes a relation between the diﬀerent resistance mech-

anisms and the stress τ

∗

. It can be used to calculate the equilibrium position

on the entrance side of the dislocation in the particle, which is dependent

on τ

∗

. Even in the simple case that the obstacle resistance consists only of

aforceK

at the border of the cutting plane, the obstacle resistance force

F = τ

∗

lb is not equal to 2K

. This led Kocks, Argon and Ashby [9] to the

conclusion that the respective activation distance Δd need not be equal to

the diﬀerence between the equilibrium x coordinates at the exit and entrance

sides of the particle, x

−x

.Tosolvetheproblem,from geometric consider-

ations, they suggested a straight extrapolation of the dislocation outside the

particle to the symmetry line (x axis) leading to the reaction coordinate

KAA

= x − z cot φ.

4.7 Overcoming of Extended Obstacles 119

However, it can be shown that simple interaction proﬁles constructed by using

this formula and (4.70) violate the thermodynamic relation (4.5). To calculate

the force–distance laws of overcoming the extended obstacles, the Gibbs free

energy of activation ΔG can be established considering the “chemical” terms,

that is, the work against the forces K

and K

and against the friction stress

, as well as the energy changes due to the changing length of the dislocation

line inside and outside the particles [217]. According to (4.3), the work of

the external stress τ

∗

by sweeping the area V/b has to be subtracted. All

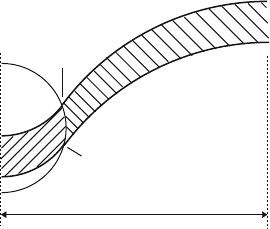
terms have to be taken between the stable equilibrium position x

of the

dislocation on the entrance side of the particle and the labile equilibrium

position x

on the exit side, as outlined in Fig. 4.25. These positions depend

on τ

∗

and are obtained by (4.70). Diﬀerentiating ΔG with respect to τ

∗

yields

the activation volume V after (4.5). For the extended obstacles, a description

in terms of V and τ

∗

is more meaningful than that in terms of Δd and F as

the relation F = τ

∗

bl (4.2) is valid only for z  l.

The result of the calculation is very simple [217]. The activation area V/b

equals the area swept by the dislocation between the entrance and exit posi-

tions as indicated by the hatched area in Fig. 4.25. This is independent of the

acting resistance mechanisms. The formulae show that, in general, the activa-

tion distance Δd = V/(bl) is not equal to the diﬀerence of the x coordinates

− x

. Exceptions are only cases with z

= z

To illustrate the results, several cases of particles of octahedral shape with

a rhombic cutting plane are calculated in [217]. Such particles act as obstacles

in crystals with the NaCl structure like MgO [218]. Figure 4.26 shows the

central and a noncentral cutting plane. At the borders, the slope is piecewise

constant (for edge dislocations x



=0.707 on the entrance side and x



−0.707 on the exit side). Edge and screw dislocations intersect the particles

in diﬀerent ways. Figure 4.27 compares the V vs. τ

∗

curve with the simple

− x

vs. τ

∗

curve in a normalized way for a particle with a friction stress

inside the particle and a diﬀerence between the dislocation energies in the

particle E

and the matrix E

. Except for τ

∗

= 0, the normalized activation

l/2

Fig. 4.25. Half of an extended obstacle and the dislocation line in the entrance and

exit positions. The hatched area is the activation area