Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

140 4 Dislocation Motion

− f

) Ω

bkT

Then, (4.85), (4.87), and (4.88) yield the climb velocity of the dislocation as

≈ D

. (4.90)

This is the classical Einstein relation between the diﬀusion rate and the

applied force for climb via the motion of jogs. The activation energy is the

self-diﬀusion energy plus the jog formation energy, ΔG =ΔG

+ΔG

ΔG

4.10.4 Diﬀusion-controlled Climb

The preceding derivation of the climb velocity of dislocations is based on the

condition that the applied forces are not very small and that there is no con-

centration gradient of point defects around the dislocations. This means that

the emitted defects diﬀuse fast enough away from the dislocations or that the

defects to be absorbed diﬀuse fast enough towards them. If this is not the

case, the dislocations become saturated with vacancies and a concentration

gradient develops around them. Then, the climb velocity is no longer deter-

mined by the process of emission or absorption of the point defects at the

dislocations but by the diﬀusion ﬂux owing to the concentration gradient. It

was shown in [246,247] that this situation holds in many experiments. During

diﬀusion-controlled climb, the ﬂux of vacancies emitted or absorbed by the

dislocation has to be equal to the ﬂux through some border face around the

dislocation [248]. If the dislocation climbs at a velocity v

, the ﬂux per dis-

location length is J = v

b sin β/Ω. It is determined by a diﬀusion problem

around the dislocation applying Fick’s law

J =

b sin β

grad c. (4.91)

The solution depends on the proper boundary conditions and contains a char-

acteristic length l

. For a climbing straight dislocation in an environment

of other parallel dislocations of both signs, suitable boundary conditions are

given by a cylinder of radius R around the dislocation. Outside this radius,

the concentration of point defects equals the equilibrium concentration with-

out stress, c ≈ c

.ThevalueofR is about half the distance between the

dislocations, similar to the outer cut-oﬀ radius for determining the disloca-

tion energy (Sect. 3.2.2). The characteristic length is then l

≈ b ln(R/b). The

climb velocity (i.e., the velocity in the direction perpendicular to b and the

line vector ξ)is[12]

2πD

sin βkTln(R/b)

, (4.92)

4.10 Dislocation Climb 141

or, neglecting the weak dependence on R, it becomes

≈

sin βkT

. (4.93)

This equation is very similar to that for emission or absorption-controlled

climb (4.90), except that the jog concentration is not contained. The transi-

tion to saturation of the dislocation with vacancies begins when the distance

between the jogs l

in (4.88) becomes smaller than the characteristic diﬀu-

sion length l

. For thermal jogs, this occurs at high temperatures. In an exact

way, the climbing dislocation should be treated by a diﬀusion problem in a

moving reference system. However, under usual climb conditions, the above

static solution is suﬃcient. Other geometric conﬁgurations of the dislocations

lead to diﬀerent estimates of the characteristic length l

.Animportantcase

is the climb under the attractive force between the dislocations of an edge

dislocation dipole. It is a mechanism of recovery of the dislocation density.

Both dislocations are located near the center of the cylinder and both emit

or absorb vacancies simultaneously into the neighborhood. The climb velocity

of each of the two dislocations is then approximately half of that of a single

dislocation under the same force.

The activation energy for diﬀusion-controlled climb is the self-diﬀusion

energy ΔG

=ΔG

+ΔG

. For emission or absorption-controlled climb,

the jog formation energy ΔG

has to be added. As for low climb forces in all

formulae the climb velocity is proportional to the climb force and accordingly

also to the climb component of the stress, the stress exponent m of (4.10) is

equal or close to unity. The activation volume is very small, approximately

the atomic volume Ω.

In several diﬀusion problems, diﬀusion along preferred paths is important.

Such preferred paths are the cores of the dislocations. The diﬀusion along the

dislocation cores is termed pipe diﬀusion. Its activation energy is consider-

ably lower than the self-diﬀusion energy, down to half of it. Pipe diﬀusion

plays a role in climb processes driven by the line tension of the dislocations,

for example, in changes of the shape of prismatic dislocation loops due to

nonconservative dislocation motion.

4.10.5 Jog Dragging

For climb of a dislocation as a whole, as it was treated above, the work term

like f

Ω/b = σ

Ω in (4.85) is small so that almost the whole diﬀusion energy

has to be expended. Usually, this is possible only by the help of thermal

activation at high temperatures. An exception is a dislocation with a high

screw component and a relatively low jog density subjected to a glide stress.

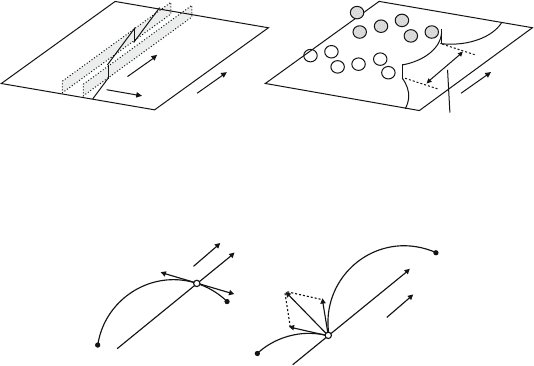
Figure 4.36a shows such a dislocation with two jogs J of atomic height and

opposite sign. In principle, the jogs can glide in the direction of the Burg-

ers vector, that is, along the shaded areas. However, diﬀerent processes may

142 4 Dislocation Motion

Fig. 4.36. Jog dragging. (a) Dislocation with near-screw character containing two

jogs J and slip planes of the jogs (shaded areas). (b) Emission of diﬀerent types of

point defects by jog dragging

Fig. 4.37. Equilibrium conﬁgurations of jogs with respect to glide. (a) Glide

conﬁguration. (b) Conﬁguration with climb force

prevent glide. The ﬁrst one is of dynamic nature. Because of the large screw

component, the jogs have to glide much faster than the other parts of the

dislocation. Besides, usually the jogs have to glide on a crystallographic plane

diﬀerent from the main slip plane of the dislocation. Both processes lead to a

higher glide resistance of the jogs so that they cannot follow the main parts

of the dislocation by glide alone. In pure screw dislocations, there is no glide

force at all acting on the jogs. Localized obstacles pinning the dislocation

inﬂuence the motion of the jogs. As pointed out in [249, 250] and outlined in

Fig. 4.37, a jog (open circle) situated between two localized obstacles (solid

dots) can have two equilibrium conﬁgurations with respect to glide. The arrow

indicates the line parallel to the Burgers vector along which the jog can glide.

In Fig. 4.37a, the line tensions of the segments adjoining the jog cancel each

other so that there is neither a glide nor a climb force resulting. In Fig. 4.37b,

the glide components cancel each other but there remains a force F

in climb

direction. When a jog is formed by dislocation intersection, a deep cusp devel-

ops in the dislocation line because of the strong elastic interaction between

the cutting dislocations. Consequently, intersection jogs will be generated in

the conﬁguration of Fig. 4.37b. Thus, the presence of localized obstacles sta-

bilizes jogs in the their nonconservative conﬁgurations. A model of stage I

deformation was based on these ideas [251].

If the jogs in near-screw dislocations cannot glide sidewise, the segments

of length l

between the jogs bow out under stress as in Fig. 4.36b. While

for climb of a straight dislocation, the climb force acting on a jog is F

jog

h = σ

hb sin β ((4.80) and (4.81)), it now becomes F

jog

= τ

∗

(4.2).

4.11 Drag Forces due to Point Defect Atmospheres 143

Accordingly, the glide velocity of the dislocation controlled by the climb of

the jogs is given by

= bν

exp



−

ΔG

+ΔG

− τ

∗



. (4.94)

This process is called jog dragging (see, e.g., [252,253]). Here, the activation

distance was set to b. The activation energy comprises the energy of formation

of the point defects ΔG

and their migration ΔG

, as the defects have to be

separated from the jog. Separation could also occur by sidewise glide of the

jog. However, if sidewise glide were easily accessible, the jog had glided away

before the point defect had formed. Thus, if the jog moves by the creation of

point defects, the migration energy has to be taken into account. In Fig. 4.36,

the two jogs are of diﬀerent sign. Accordingly, one jog is a vacancy-producing

jog while the other one is an interstitial-producing jog. At low velocities and

small stresses, the interstitial jog moves by absorbing vacancies. However, the

concentration of available vacancies limitsthisprocesssothatathighstresses

the jog has to produce interstitials. As their formation energy is mostly much

higher than that of vacancies, the interstitial jogs represent stronger obstacles

controlling the total dislocation velocity.

The jog distance l

can be several orders of magnitude larger than h.

As a consequence, the work term F

jog

b = τ

∗

can now assume a large

fraction of the self-diﬀusion energy, thus enabling jog dragging even at quite

low temperatures like room temperature. Accordingly, the activation energy

depends strongly on the stress. The activation volume is given by V = b

which is comparable to that of localized obstacles. However, there are clear

diﬀerences between both processes. Jog dragging is not subject to Friedel

statistics, and the forward slip distance after successful thermal activation is b

but not l

. The jogs are created by dislocation intersection, they are certainly

not in thermal equilibrium. The segment length l

can therefore vary during

plastic deformation.

Jog dragging, that is, climb of jogs driven by the glide component of the

applied stress ﬁeld including the creation of isolated point defects, is restricted

to jogs of only very few atomic distances in height. Higher jogs drag dislocation

dipoles, so-called debris. This process is discussed in Sects. 5.1 and 5.2. Jog

dragging is thought to contribute to the thermal part of the ﬂow stress and to

be a main process of the generation of point defects during plastic deformation.

However, the parameters of the model may vary to a large extent, impeding

the identiﬁcation by macroscopic tests.

4.11 Drag Forces due to Point Defect Atmospheres

The hydrostatic stress ﬁeld of dislocations changes the equilibrium concen-

trations of intrinsic and extrinsic point defects near the dislocation cores.

Therefore, atmospheres form with point defect concentrations deviating from

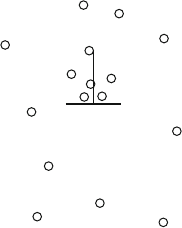
144 4 Dislocation Motion

Fig. 4.38. Vacancy atmosphere around an edge dislocation

the stress-free equilibrium concentration thus reducing the total energy of the

system of dislocations and point defects. While moving, the dislocations are

shifted away from the centers of the atmospheres, which are dragged behind.

This is connected with an increase in energy and a respective friction force.

These processes will be discussed below.

The edge components of dislocations involve a hydrostatic stress ﬁeld plot-

ted in Fig. 3.9a, b and given by (3.30) and (3.31). ϕ is the coordinate angle

around the dislocation. The latter equation describes a region of hydrostatic

compression on the side of the inserted half-plane of the dislocation, and a

region of tension on the opposite side. Inserting the distribution of the pressure

around the dislocation into (4.76) reveals an increased equilibrium concentra-

tion of vacancies and a decreased concentration of interstitials in the region of

compression. The opposite behavior is observed for the tension side as illus-

trated for the vacancies in Fig. 4.38. The above treatment is valid for the edge

component of straight rigid dislocations. Straight screw dislocations do not

react with the centers of expansion or dilatation. However, as the stress ﬁeld

of such an elastic inclusion is of pure shear character, the dislocations will not

remain straight. Instead, they develop a wavy shape where an initially straight

screw dislocation also contains parts with an edge component so that both

edge and screw dislocations interact with the centers of dilatation. Besides,

higher-order eﬀects in the pressure become important at the high stresses

close to the dislocation cores. These eﬀects result in an attractive interaction

between vacancies and all types of dislocations.

In alloys, foreign atoms solved in the matrix essentially determine the

dislocation mobility. The solute atoms can either be placed on regular lattice

sites to form a substitutional alloy, or they are situated on interstitial sites.

In both cases, the defect can be approximated by a spherical elastic inclusion

as done for intrinsic point defects and outlined in Sect. 3.2.6. If the solute is

inserted near a dislocation with its ﬁeld of hydrostatic pressure p around it,

the reversible work of insertion is given by p (Ω

− Ω)=pΔΩ,whereΩ is

the atomic volume, and Ω

is the volume of the solute. This work changes the

4.11 Drag Forces due to Point Defect Atmospheres 145

concentration of solutes around the dislocation from the average (equilibrium)

concentration c

= c

exp



−

pΔΩ



. (4.95)

Inserting the interaction constant β from (3.32), there follows a distribution

of the solutes around the dislocation as

= c

exp



−

β sin ϕ

rkT



. (4.96)

The distribution is very similar to that of intrinsic point defects as pre-

sented in Fig. 4.38. Solutes with Ω

<Ωaccumulate on the compression side

of the dislocation, while the dilatational region is depleted. Again, the energy

of the dislocation is reduced by the formation of the solute atmosphere. Inte-

grating the solute distribution in a cylinder around the dislocation with an

inner and outer cut-oﬀ radius shows that the dislocation accumulates solute

atoms. With characteristic values of the solutes, in a 2% alloy about one solute

atom per atomic plane segregates in the elastic stress ﬁeld of the dislocation

at about 300

◦

C [12]. Additional solute atoms can segregate in the disloca-

tion cores. This process is described by a binding energy between solute and

dislocation. The possibilities of arranging the solutes in the dislocation core

depend on the crystallographic direction of the dislocation line. This eﬀect

may promote particular orientations of the dislocations, which need not cor-

respond with the directions of the Peierls valleys. Further elastic interactions

between dislocations and solute atoms were pointed out in Sect. 3.2.6.

For dislocations dissociated into partial dislocations, solute segregation

eﬀects at the stacking faults may be important. As at the stacking fault,

the regular stacking sequence is violated, the energy of a solute at the fault

plane will, in general, diﬀer from that in the undisturbed matrix. Therefore,

also the equilibrium concentration at the fault will diﬀer from that in the

bulk. The problem is treated in the framework of adsorption theory. Solute

atoms can be attracted or repelled by the fault, leading to the accumulation

or depletion of solutes. In both cases, the fault energy is reduced, yielding an

increased dissociation width of the dislocation (e.g. [254]). During the motion,

the dislocation is dragged out of its equilibrium conﬁguration, resulting in a

friction force. This mechanism was ﬁrst suggested by Suzuki [255,256] and is

called Suzuki eﬀect. For a review see [257].

If the dislocation is moved under the action of a shear stress τ, it is dragged

out oﬀ its equilibrium solute atmosphere described by (4.96). Here, c

is the

solute concentration at r = ∞. With the displacement x of the dislocation

with respect to the frozen-in atmosphere, the necessary force per unit length

of the dislocation is

F = τb =

∂W(x)

L∂x

L is the dislocation length and W (x) is the reversible work to drag the dis-

location out of the cloud. It is given by W (x)=β sin ϕ/r or, in cartesian

146 4 Dislocation Motion

coordinates,

W (x)=

βy

+ y

The force the displaced solute atmosphere exerts on the dislocation is

equal to that the dislocation exerts on the atmosphere. Thus, the atmosphere

is driven to move with the dislocation. The respective diﬀusion problem is

a very complex two-dimensional one. It was ﬁrst attacked by Cottrell and

Jawson [258] and Cottrell [259]. The eﬀect is therefore called Cottrell eﬀect,

and the solute cloud Cottrell atmosphere. The treatment was revised by Hirth

and Lothe [12]. It is reduced to a one-dimensional problem of the diﬀusion

in a moving potential well in layers parallel to the slip plane. The solutions

depend on the dislocation velocity. At low velocities, the distribution of the

solute concentration around the dislocation is close to the equilibrium distri-

bution (4.96), and this distribution diﬀuses with the dislocation. Its velocity

is given by

τb

DkT

ln (y

)

. (4.97)

D is the diﬀusion coeﬃcient and y

and r

are cut-oﬀ parameters. The outer

cut-oﬀ radius is given by y

= D/v

as long as it is smaller than the distance

R between the dislocations or the size of the crystal. Otherwise, y

= R.In

the ﬁrst case, the dependence of the velocity on the force or stress is not

linear. The inner cut-oﬀ radius r

= β/(kT) limits the range in which the

many assumptions of the calculation are valid. If r

turns out to be smaller

than the usual inner cut-oﬀ radius r

, r

can be replaced by the latter.

At high dislocation velocities, the Cottrell atmosphere is distorted, reduced

in size, and the concentration of the solutes tends towards the equilibrium

concentration c

.Aboveacriticalvelocityv

, the dragging stress even starts

to decrease with increasing velocity. In the high-velocity range, the extension

of the Cottrell atmosphere is no longer controlled by diﬀusion, that is, by a

random motion of the solutes, but by the directional drift in the stress ﬁeld of

the dislocation. In the upper range with no solute cloud left, the dislocation

velocity shows a reciprocal dependence on the stress

πc

Dβ

τb

. (4.98)

In the intermediate range, no analytical treatment is available but the lim-

iting behavior suggests the existence of a maximum drag stress. Figure 4.39

presents a schematic plot of the velocity dependence of the drag stress. The

abscissa is a logarithmic axis either of the dislocation velocity or, via the

Orowan equation (3.5), of the plastic strain rate ˙γ. As in thermal activation

theory, an increase in the logarithm of the rate corresponds to a decrease in

temperature, the abscissa can also be read in opposite direction as a temper-

ature axis. Three ranges of the curve can be distinguished, the low-velocity

region A with an increasing drag stress and a diﬀusing Cottrell atmosphere,

4.11 Drag Forces due to Point Defect Atmospheres 147

Fig. 4.39. Schematic representation of the dependence of the drag stress due to

the interaction between dislocations and solute atoms on the dislocation velocity.

Ranges A and B are controlled by the Cottrell atmosphere, in range C the solutes

act as localized obstacles

the high-velocity range B with a decreasing drag stress and a reduced atmo-

sphere moving by drift, and ﬁnally region C at very high velocities where the

solutes can be considered ﬁxed and acting as localized obstacles.

The more exact treatment of the Cottrell eﬀect in [258] yields estimates

of the critical dislocation velocity v

and the maximum drag stress τ

max

˙γ

b

≈

4 DkT

and (4.99)

max

≈

17 c

. (4.100)

Several more reﬁned calculations have shown that the numerical factors

especially in (4.100) are uncertain up to factors of about 5.

The rate or temperature dependence of the drag stress of Fig. 4.39 and

the respective dislocation behavior show some remarkable features. The most

important one is the anomalous increase of the drag stress with increas-

ing temperature in range B. This is one possibility to explain the so-called

ﬂow stress anomalies in some alloys and particularly in several intermetal-

lic alloys. Figure 4.40 presents an example of the intermetallic alloy FeAl,

where the ﬂow stress anomalously increases between about 250 and 550

◦

The mechanisms of the ﬂow stress anomaly will be described in more detail in

Sect. 9. Irrespective of the active mechanism in FeAl, (4.100) can be used for a

rough estimate of the concentration of solutes necessary to explain a signiﬁcant

contribution of the Cottrell eﬀect to the ﬂow stress. In Fig. 4.40, the anoma-

lous increase of the ﬂow stress amounts to about τ

max

=2× 10

−3

μ.Witha

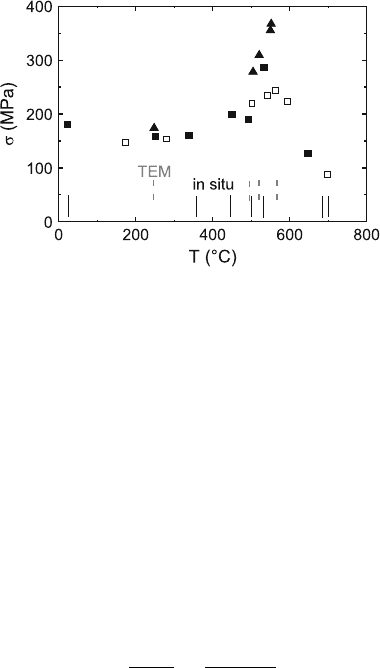
148 4 Dislocation Motion

Fig. 4.40. Temperature dependence of the ﬂow stress in Fe-43 at% Al single crystals

loaded along a [753] axis. Solid symbols: initial ﬂow stress of individual experiments.

Open symbols: ﬂow stress after temperature changes corrected for work-hardening.

Triangles :˙ε =10

−4

−1

. Squares:˙ε =10

−5

−1

. Dashed grey vertical lines indicate

temperatures of TEM studies of the dislocation structure, and black vertical lines

those of in situ straining experiments. Data from [8]

diﬀerence in the atomic volumes of the solute and the matrix of ΔΩ =0.1 b

and ν =0.3 in (3.32), the necessary solute concentration is c

≈ 5 × 10

−3

Thus, solute concentrations of the order of magnitude of several 1,000 ppm

are necessary to reach a remarkable contribution of the Cottrell eﬀect to the

ﬂow stress.

In a plot like Fig. 4.39, with the stress plotted as a function of the logarithm

of the strain rate, the slope of the curve ∂τ/∂ ln ˙γ is directly related to the

strain rate sensitivity

r =

∂σ

∂ ln ˙ε

∂τ

∂ ln ˙γ

is the orientation factor. In the same ﬁgure, in range C of the action of

localized obstacles, the curve is bent upwards, that is, the strain rate sensi-

tivity r increases with increasing strain rate ˙γ or stress τ. This is the normal

behavior of thermally activated processes. Contrary to that, in the low veloc-

ity range A of the Cottrell eﬀect, the curve tends to the maximum at v

That means that the strain rate sensitivity decreases with increasing strain

rate or stress towards zero. In the present book, this behavior is called an

inverse dependence of the strain rate sensitivity r on the strain rate ˙γ or the

stress τ . Finally, in range B of the curve, the strain rate sensitivity is negative.

Then, the deformation is unstable as the ﬂow stress decreases with increasing

strain rate. Such plastic instabilities will be described in Sect. 5.3.

In the above three ranges, the kinematic behavior of the dislocations is

diﬀerent. In the normal range C, the behavior depends on the mechanism

controlling the dislocation mobility. When the action of the solutes as local-

ized obstacles is signiﬁcant, the dislocation motion is jerky on a microscopic

scale. In the stable range A of the Cottrell eﬀect, the dislocation motion is

4.11 Drag Forces due to Point Defect Atmospheres 149

smooth and viscous, while in the unstable range B dislocations frequently are

generated in avalanches, moving very fast until the stress is relaxed to a value

where only a slow steady motion is possible.

The segregation of solute atoms at dislocations is frequently designated

as strain ageing. In static strain ageing, the resting dislocations acquire their

equilibrium solute clouds. To break the dislocations away from their solute

clouds requires a stress much higher than that for steady state motion. This

leads to a temporary increase of the stress followed by a decrease, that is, a

yield point or yield drop eﬀect. In dynamic strain ageing, the mobility of the

dislocations is controlled by the Cottrell eﬀect or a similar mechanism. This

is often associated with a very low or even negative strain rate sensitivity

and with plastic instabilities. Point defect atmospheres may arise not only

from extrinsic point defects but also from intrinsic ones as described above

and illustrated in Fig. 4.38. This topic will be discussed in more detail in

Sect. 9. In materials with a high Peierls stress, the segregation of solutes to

dislocations is treated in [260].

Point defects with a tetragonal stress ﬁeld may orient in the stress ﬁeld

of the dislocations and give rise to the induced Snoek eﬀect. Such defects

are, for example, interstitials in the dumbbell conﬁguration or divacancies or

associates between an aliovalent impurity atom and a charge-compensating

vacancy in ionic crystals. In stress-free cubic crystals, the orientations of these

defects are equally distributed over the three equilibrium orientations. In the

stress ﬁeld of a dislocation, the defects may orient so that the three equi-

librium orientations are no longer equally occupied. These so-called Snoek

atmospheres may be dragged together with the moving dislocations, similar

to the Cottrell atmospheres. Here, only the orientational state of the solutes

moves with the dislocations without a net solute diﬀusion. After the dislo-

cations have moved away, the oriented state relaxes so that the equilibrium

orientations are again equally occupied. The problem has been attacked by

Schoeck and Seeger [261]. They show that the maximum drag stress of the

induced Snoek eﬀect occurs when the dislocation moves during the relaxation

time t

rel

=1/ω just over the width r

of the potential well. Thus, the critical

velocity at the ﬂow stress maximum is given by

rel

= r

ω.

The diﬀusion jump frequency ω is given by a formula similar to that for the

motion of kinks (4.34), with the migration energy of the moving point defect.

Hirth and Lothe [12] solve the problem similarly to the Cottrell problem,

which for the dislocation velocity in the limiting low-velocity range yields

3τb

2πc

with c

being the concentration of the tetragonal defects. The drag stress in

the high-velocity drift region reads