Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

130 4 Dislocation Motion

a “relativistic” transformation is applied in analogy to the electro-magnetic

case. The displacement ﬁeld of the screw dislocation can then be written as

(x, y, t)=

2π

arctan

ηy

x − v

with

η =



1 −

Here, v

is the dislocation velocity and c

is the transverse sound wave velocity.

For v

= 0, this formula equals (3.7). For v

approaching c

,thatis,η → 0,

the stress ﬁeld is distorted in such a way that, compared to the static case,

the stresses are lower in x direction and higher in y direction. In the limit of

= c

, the stresses are zero in x direction and inﬁnite along y.Ofcourse,

the linear elasticity theory applied breaks down for these high stresses. The

energy per unit length of the moving screw dislocation can be expressed as

= E

/η,

where E

is the respective energy of the resting screw dislocation (3.13).

In relativistic mechanics, there is the same relation between energy and rest

energy of a moving body. If 1/η is expanded to the ﬁrst power of v

,for

certain boundary conditions, the energy of the moving screw dislocation can

be written as

= E

The factor m

= E

can be called the eﬀective mass of the dislocation

per length, in analogy to the respective formula in mechanics.

The described properties of dislocations together with eﬀects of elastic

nonlinearity lead to the conclusion that the respective sound velocity is a

limiting velocity of the dislocation motion. Nevertheless, supersonic motion is

possible if the dislocation gains energy by transformation of the range close to

the slip plane into a state of lower energy, for example, by the motion of a single

partial dislocation removing the attached stacking fault. Atomistic simulations

have shown that a dislocation subjected to high stresses and created in the

supersonic state at a strong stress concentration can continue to move at

velocities higher than the respective sound velocity [230].

In the limit of linear elasticity theory, dislocations move at subsonic veloc-

ities without radiation of energy and without friction. However, elastic waves,

that is, phonons, are scattered at the dislocations and transfer momentum to

them. This scattering of thermal elastic waves results in a viscous damping

of the dislocation motion at ﬁnite temperatures [231, 232]. In addition, the

discreteness of the crystal lattice expressed by the Peierls barriers has to be

considered, leading to the radiation of phonons from the dislocation cores.

A further contribution to the drag stems from the scattering of conduction

4.9 Dislocation Motion at High Velocities and Low Temperatures 131

electrons in metals [233]. The viscous drag force due to phonon and electron

damping is proportional to the dislocation velocity, that is,

= τ

∗

b = Bv

, (4.74)

where f

is the force per unit length, and B is the viscous drag coeﬃcient.

According to Leibfried’s theory [231], the temperature dependence of the drag

coeﬃcient is given by

B =

3kTz

20c

Here, z is the number of atoms per unit cell. The linear temperature depen-

dence was conﬁrmed in [234] by molecular dynamics simulations using an

embedded atom potential. The electron scattering contribution to the damp-

ing is supposed to be independent of the temperature. Turning to the

superconducting state, it freezes out, resulting in a softening of the materials

as ﬁrst observed in [235–237], reviewed in [238] and recently in [239]. Other

quantum eﬀects at low temperatures are quantum-mechanical tunneling and

the zero point vibrations of the dislocation segments adjoining localized obsta-

cles. The ﬁrst quantitative theory of these eﬀects was given in [240]. These

eﬀects also result in a softening with respect to the Arrhenius relation. A

dislocation moving in the ﬁeld of the Peierls potential periodically accelerates

and decelerates, resulting in the emission of lattice waves. Simulations in [241]

proved that this process results in an energy loss, which is not proportional

to the dislocation velocity and which is about one order of magnitude larger

than the theoretical value of the phonon scattering mechanism.

To summarize the results on the dynamic behavior of dislocations at high

speed and/or low temperature, the equation of motion of a dislocation segment

can be established as

∂

∂t

− Γ

∂

∂z

+ B

∂x

∂t

= bτ

∗



. (4.75)

The ﬁrst term stems from the dislocation inertia. The second term results from

the line tension of the dislocation curvature. The third term represents the

dynamic dislocation drag. On the right side of the formula are the forces due

to the external stress and the sum of the internal forces due to other defects in

the lattice. To model thermally activated dislocation motion, random forces

can be added as done, for example, in [210].

In summary,

• Dislocations move viscously at high speeds and suﬃciently high temper-

atures, and their mobility is controlled by the dynamic drag coeﬃcient

• At (very) low temperatures, the dislocation motion is underdamped and

inertial eﬀects become important. They cause a short dynamic overshoot-

ing of the force acting on obstacles with respect to the overdamped case

and result in a softening of the material.

132 4 Dislocation Motion

• A softening is also observed after transition to the superconducting state. It

is explained by both the direct consequence of the reduction of the damping

coeﬃcient B and the resulting increase of the importance of inertial eﬀects.

4.10 Dislocation Climb

Up to this point, dislocation motion has been treated at temperatures where

diﬀusion jumps are slow compared to the elementary steps of dislocation

motion. Thus, the obstacles to glide were considered immobile. In the fol-

lowing sections, dislocation motion at high temperatures will be discussed

where diﬀusion cannot be neglected. The ﬁrst case is dislocation climb intro-

duced in Sect. 3.1.2 with a point defect ﬂux to or from the dislocations. This

process can be driven by the applied stress or by chemical forces resulting

from non-equilibrium point defect concentrations. Climb is an intrinsic mode

of dislocation motion in cases where glide is suppressed, for example, in hexag-

onal metals loaded along the c axis, where the glide systems with the basal

and prism planes have zero orientation factors for glide [242,243]. Climb also

is the dominating mode of dislocation motion during plastic deformation of

quasicrystals as described in Chap. 10. In most cases, climb occurs in addition

to glide, playing an important role in recovery processes where the disloca-

tions stored during the deformation form low energy structures, which cannot

be reached by glide alone, or where the dislocations even annihilate each

other (Sect. 5.1.3). Besides climb, diﬀusion-controlled processes without a dif-

fusion ﬂux to or from the dislocations may inﬂuence the dislocation mobility.

Point defects have elastic (and other) interactions with the dislocations, which

result in point defect atmospheres around the dislocations consisting of both

intrinsic (vacancies and interstitial atoms) and extrinsic point defects (for-

eign atoms), or of clouds of oriented states of defects with nonspherical stress

ﬁelds. These atmospheres are dragged with the moving dislocations causing

a frictional force. These processes are described in Sect. 4.11. To understand

diﬀusive processes during dislocation motion, ﬁrst point defect equilibria will

be discussed.

4.10.1 Point Defect Equilibrium Concentrations

In a similar way, as a straight dislocation is not the state of lowest Gibbs

free energy but contains an equilibrium concentration of kinks at a ﬁnite

temperature (Sect. 4.2.2), the equilibrium state of a crystal contains certain

equilibrium concentrations of intrinsic point defects. The derivation of the

equilibrium concentrations is based on the same ideas as that for kinks.

The increase in the free energy by the formation energy of the defects is

compensated by the conﬁgurational entropy arising from the many diﬀerent

possibilities to arrange the defects. An intrinsic point defect is introduced into

a crystal if an atom from a ledge in a surface step is removed and inserted

4.10 Dislocation Climb 133

into the interior of the crystal to form an interstitial, or it is removed from the

interior and placed at a ledge of a surface step to form a vacancy. The pro-

cess is connected with a change in the external volume of the crystals ΔV

ext

In analogy with (4.29), the atomic equilibrium concentration of interstitials

or vacancies, that is, the concentration related to the number of possible

interstitial or vacancy sites, is given by

=exp



−

ΔG



, (4.76)

where ΔG

is the Gibbs free energy of the formation of the point defects. The

formation energy ΔG

is calculated in isotropic elasticity theory by inserting

a small sphere into a hole, which is either too small or too large for it. As in

closed-packed structures there is no space for the interstitials, they are strong

centers of repulsion, with their formation energies being high (several electron-

volt). Consequently, in most materials the concentration of vacancies is much

higher than that of the interstitials. Frequently, interstitials form a so-called

dumbbell conﬁguration where two atoms share one lattice site. Instead of

spherical symmetry, these defects have a stress ﬁeld of tretragonal symmetry.

The situation is more complicated in ionic crystals because charge neu-

trality has to be maintained. Therefore, in monovalent crystals like those of

the NaCl structure, either equal numbers of vacancies in both sublattices

(Schottky disorder) have to be created, or equal numbers of vacancies and

interstitials in one sublattice (Frenkel disorder). Even mixtures of both kinds

of disorder are possible.

Point defects as centers of compression or dilatation react with the

hydrostatic components of external and internal stress ﬁelds

p = −(1/3) (σ

+ σ

) .

The interaction results in a change in the formation energy by the reversible

work pΔV

∗

. The thermodynamic formation volume ΔV

∗

is diﬀerent for

vacancies and interstitials. It is approximately equal to the atomic volume,

ΔV

∗

≈ Ω. Hirth and Lothe [12] discuss the diﬀerences in the formation vol-

ume of vacancies and interstitials in detail. Owing to the reversible work of

introducing a point defect, the equilibrium concentration with external and

internal pressures being present is given by

c =exp



−

ΔG

ﬁ

− pΩ



= c

exp



pΩ



. (4.77)

Formulae of this type are valid for all sources or sinks for point defects, that

is, outer or inner surfaces and dislocations. The latter are sources of internal

hydrostatic stresses. Accordingly, the point defect equilibrium concentrations

diﬀer near the dislocations with respect to the rest of the crystal. As long as

the equilibrium concentrations are not established, the dislocations emit or

absorb point defects and they climb. In addition, point defects can be emitted

134 4 Dislocation Motion

or absorbed at the surfaces. These processes take place until the equilibria

with all sources and sinks of point defects are attained. On the other hand,

external and internal stresses may force the dislocations to climb, resulting in

nonequilibrium concentrations of point defects. Both situations are treated in

the sections below following the presentation by Friedel [123].

4.10.2 Climb Forces

Force Required for Athermal Climb

As introduced in Sect. 3.1.2, climb motions of dislocations change the volume

of the crystal. The volume change due to a displacement of a dislocation

segment of length L and orientation ξ by dx is given by (3.3). For athermal

climb, that is, for climb caused only by the action of mechanical stresses, the

volume change is realized by the generation of vacancies or interstitials. The

force necessary follows from the number of defects to be created and their

formation energy. For pure climb, the Burgers vector b and the line vector ξ

of the dislocation are perpendicular to the displacement vector dx in Fig. 3.4.

Thus, both the cross products ξ × dx and b × dx lie in the slip plane. In

addition, b × dx is perpendicular to b so that the volume change in scalar

notation is

dV = bL sin β dx. (4.78)

β is again the angle between the Burgers vector and the line direction. If β

is small, the volume change is realized by the formation of individual point

defects. Then, the energy per dislocation length necessary for producing a

number dN of point defects is given by

=ΔG

LΩ

ΔG

is the formation energy of the respective point defects, and the atomic

volume Ω is the approximate formation volume. Introducing the volume

change from (4.78) yields

=ΔG

b sin β

dx.

The necessary climb force per dislocation length is then

cl,max

L dx

=ΔG

b sin β

. (4.79)

A rough estimation of the formation energy of a vacancy is ΔG

≈

μΩ/4 ≈ μb

/4. Accordingly, for pure climb of a pure edge dislocation

(sin β = 1), the climb force is

cl,max

μb

4.10 Dislocation Climb 135

or the required stress μ/4. This is a stress in the order of magnitude of the

theoretical yield stress of Sect. 1.1, which real crystals cannot sustain. Conse-

quently, climb usually does not take place in an athermal way as assumed here,

but in a thermally activated mode in small steps by climb of jogs connected

with diﬀusion.

Applied Climb Forces

The climb force estimated above is the force required for pure athermal climb.

The applied forces driving climb essentially have three origins.

1. The climb component of the Peach–Koehler force resulting from a mechan-

ical stress Σ. It is given by (3.23) comprisinganormalstressactingon

the edge component and a shear stress acting on the screw component of

the dislocation. The climb force per dislocation length resulting from a

uniaxial stress on a dislocation with its Burgers vector parallel to the x

axis is given by

= σ

b sin β, (4.80)

or f

= σ

b for the pure edge dislocation. The reversible work in creating

a vacancy is f

ha = f

Ω/b. Here, h is the atomic distance perpendicular to

the slip plane, and a is the atomic distance along the dislocation line. Two

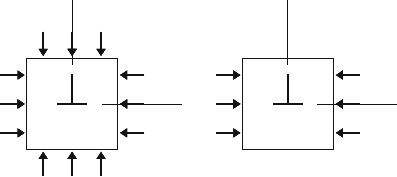
diﬀerent situations are illustrated in Fig. 4.34. In the ﬁrst one (a), an edge

dislocation is located in a crystal subject to an external pressure p.The

pressure reduces the energy of the formation of the point defects, usually

vacancies, at the surfaces by pΩ so that the equilibrium concentration of

the defects is given by (4.77). However, the energy is reduced by the same

amount also at the dislocation so that the equilibrium concentrations on

both sources or sinks are equal. Thus, after the equilibrium concentrations

have been established, the dislocation will no longer climb. A diﬀerent sit-

uation holds in Fig. 4.34b, where a uniaxial stress σ

acts on the crystal.

The uniaxial stress reduces the formation energy by σ

Ω = −pΩ. Under

Fig. 4.34. An edge dislocation in a crystal under external pressure p (a) and uniaxial

stress σ

(b)

136 4 Dislocation Motion

these conditions, the equilibrium point defect concentrations c are equal

along the dislocation and at the two outer surfaces perpendicular to the

x axis. They are given by (4.77). The equilibrium concentrations at the

other four surfaces, however, equal the concentration c

without exter-

nal stress (4.76). Consequently, there appears a point defect ﬂux between

these four surfaces and the dislocation, the dislocation climbs under the

action of the external stress σ

. This is a mechanism of high-temperature

creep (Nabarro–Herring creep [244,245]). It is observed in decagonal qua-

sicrystals as described in Sect. 10.3.2 and illustrated in the Videos 10.6

and 10.9.

Usually, climb does not occur by the displacement of the dislocation

line as a whole but by the motion of jogs along it. If a climb force acts on

the dislocation, the force on the jog of height h is given by

jog

= f

h. (4.81)

The elastic work done in shifting the jog along the dislocation and emit-

ting a vacancy is then F

jog

a = f

ha = f

Ω/b. This work, which reduces

the formation energy of the vacancy, is the same as that discussed ear-

lier. Accordingly, the equilibrium point defect concentration near the

dislocation does not depend on the structure of the dislocation.

During high-temperature deformation, not only climb processes induced

by external stressees are important but also those due to internal stresses.

They enable the formation of low-energy dislocation structures and the

annihilation of dislocations if this is not possible by glide or cross glide

alone, thus contributing to recovery.

2. The line tension of prismatic dislocation loops. Pure prismatic loops are

loops with their Burgers vector being perpendicular to the loop plane.

Thus, they are loops of pure edge dislocations, which can glide on a

cylinder deﬁned by the dislocation line and the Burgers vector. The force

follows from (3.38) as

, (4.82)

with the line tension Γ and the radius of curvature r. The line tension

drives the loops to shrink, which for prismatic loops is only possible by

climb.

3. The osmotic or chemical force. Osmotic climb forces result from sub- or

supersaturations of intrinsic point defects. To derive the osmotic force,

(4.79) is re-interpreted in the following way. If a force f acts on the dislo-

cation, it may reduce or enhance the energy of formation of a point defect

by an amount

Δ(ΔG

)=f

b sin β

Then, the equilibrium concentration of vacancies near the dislocation, for

instance, will be

4.10 Dislocation Climb 137

=exp



−

ΔG

− fΩ/(b sin β)



= c

exp



fΩ

b sin βkT



= c

exp



Δ(ΔG

)



. (4.83)

is again the equilibrium concentration of vacancies without a force

acting. The force f can be considered an osmotic force due to the sub- or

supersaturation of vacancies c

b sin β

kT ln

b sin β

. (4.84)

The osmotic force is often denominated a chemical force resulting from

the chemical potential of nonequilibrium vacancies μ

= kT ln (c

Large supersaturations of vacancies can result from radiation damage, from

plastic deformation, and from quenching the crystal from a temperature near

the melting point. The latter supersaturations can yield very high climb forces.

If a dislocation sweeps and absorbs a complete layer of voids, the actual defect

concentration is c

= 1. Inserting this into (4.84) and using (4.76) leads to

the maximum force of (4.79)

=ΔG

b sin β

= f

cl,max

Real quenching experiments do not result in such high climb forces. Nev-

ertheless, quenching from a temperature T

to a temperature T

causes a

supersaturation

=exp



−

ΔG



−



and a respective osmotic climb force

b sin β

ΔG

− T

= f

cl,max

− T

Thus, quenching the specimen from a temperature near the melting point

may lead to quite high osmotic climb forces. Point defect supersaturations

are generated also during plastic deformation. The osmotic force may then

support climb under an external stress.

4.10.3 Emission- or Absorption-controlled Climb

Similar to a gliding dislocation, which does not shift a long straight segment

from one Peierls valley to the next one but which realizes this shift by many

small steps by shifting kinks, a climbing dislocation does not move a long

straight segment in a single step. Instead, the motion takes place by emission

or absorption of individual point defects at ledges J of the inserted half-plane

138 4 Dislocation Motion

Fig. 4.35. Edge of the inserted extra half-plane of an edge dislocation with a jog J

moving from position 1 to position 2 by the emission of a vacancy V

of a dislocation as illustrated in Fig. 4.35 for a pure edge dislocation. The

ledges are identical with the jogs introduced in Sect. 3.1.2. To extend the

extra half-plane, the jog has to be shifted to the right from position 1 to posi-

tion 2. This is possible by the absorption of an interstitial or by the emission

of a vacancy V. In most cases, the latter will happen because of the usually

much higher formation energy of interstitials. Therefore, in the following only

climb via vacancies will be treated. In deriving the climb velocity of a disloca-

tion, two cases have to be distinguished. In the ﬁrst one, the concentration of

vacancies c

is uniform in the crystal, also directly near the dislocation line.

The climb velocity is then controlled by the emission or absorption of the

vacancies. They diﬀuse to or from the dislocation so quickly that a concentra-

tion gradient does not form. This case is being treated in the present section.

In the second case, vacancies are emitted or absorbed so quickly that a con-

centration gradient develops around the dislocation. Then, the climb velocity

is not controlled by the emission or absorption of the point defects but by the

diﬀusion problem around the dislocation. This will be discussed in the next

section.

The emission rate of a vacancy at a jog under the action of an external

force can be written as

forw

= nν

exp



−

ΔG

+ΔG

− f

Ω/b



forw

is the rate of forward motion under the force f

. The activation energy

implies the formation energy of the vacancy ΔG

, as the vacancy has to be

created, as well as the migration energy ΔG

, since the vacancy has to be

separated from the jog. The sum of these energies is reduced by the reversible

work done by the applied force. ν

is again an attempt frequency (vibration

frequency of the jog). n is the coordination number, which is the number of

lattice sites neighboring the jog. In the f.c.c. lattice, n = 11. The backward

jumps are controlled by the concentration of vacancies that might jump to

the jog being annihilated. By analogy with (4.77), the concentration near

4.10 Dislocation Climb 139

the jog is

=exp



−

ΔG

− f

Ω/b



A vacancy can perform a diﬀusional jump to the jog from each of the n

neighboring lattice sites so that the rate of backward jumps is

backw

= nν

c exp



−

ΔG



= nν

exp



−

ΔG

+ΔG

− f

Ω/b



The velocity of the jogs along the dislocation is

sin β

(ν

forw

− ν

backw

)

nν

sin β

exp



−

ΔG

+ΔG



exp

bkT

− exp

bkT



≈

b sin β



exp

bkT

− exp

bkT



. (4.85)

In this equation,

≈ nν

ab exp



−

ΔG

+ΔG



(4.86)

is the self-diﬀusion coeﬃcient via vacancies. The migration of the jogs results

in a dislocation velocity

= v

sin β, (4.87)

where

sin β

(4.88)

is the jog concentration along the dislocation, and l

is the distance between

the jogs. sin β takes into account that only lattice sites of the edge component

of the dislocation are considered. The sin β terms in (4.85) and (4.87) cancel

each other. If the jogs are in thermal equilibrium, their concentration is

=exp



−

ΔG



, (4.89)

with ΔG

being the formation energy of jogs. As discussed in Sect. 3.2.5, the

jog energy is approximately equal to the core energy (3.16) ΔG

≈ μb

/10,

which is not a high energy so that the thermal jog density is high at high

temperatures. At low temperatures and high climb stresses, jogs can nucleate

in a way similar to that described for kinks (Sect. 4.2.2). For small forces, the

bracketed terms in (4.85) can be approximated by