Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

100 4 Dislocation Motion

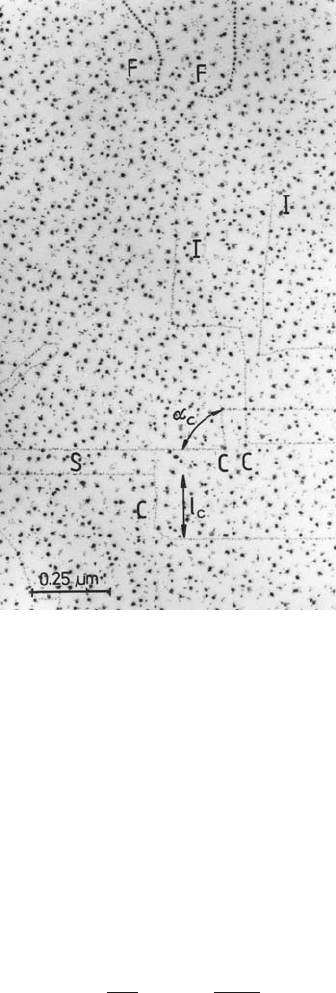
Fig. 4.12. Double decoration micrograph of a latent hardening experiment with

forest dislocations F marked by beginning cleavage steps decorated with large gold

nuclei and slip lines of the second deformation decorated with small palladium nuclei

and running horizontally, with cross slip C and immobilization events I. From [181]

conﬁguration, it has to be unlocked, that is, to be transformed into a glis-

sile state. The core transformations can be assisted by thermal activation,

leading to a state of higher or lower energy. Unlocking transformations into a

state of higher energy are only possible under the action of an external stress.

The theory is similar to that of the formation of a critical kink pair in the

double-kink mechanism (Sect. 4.2.2). The probability of unlocking or forming

a critical bulge is given by

exp



−

ΔF



where ν

is again the Debey frequency, L

∗

the width, and ΔF

the formation

energy of the critical bulge.

4.5 Overcoming of Localized Obstacles 101

The transformation into a core of lower energy is similar to the process of

cross slip of an extended dislocation as described, for example, in [183] with

an activation energy similar to that of a constriction. The transformation may

lead to a glissile conﬁguration as for cross slip, or to a sessile one. In the latter

case, the dislocation becomes locked. The probability of locking is given by a

formula similar to that above for unlocking with an activation energy ΔF

lock

A dislocation can move by a succession of locking and unlocking events.

This process is similar to the kink pair mechanism as noted in [184]. A

detailed theory was developed in [185]. The activation energy is the diﬀerence

ΔF

− ΔF

lock

between the energies of unlocking and locking. The proper-

ties of the mechanism resemble in some aspects the double-kink mechanism,

in particular with respect to the occurrence of long straight dislocation seg-

ments oriented along crystallographic directions. However, in contrast to the

Peierls mechanism, the dislocations move jerkily over distances remarkably

larger than those between the Peierls valleys. Besides, if dislocation segments

are pinned between obstacles, macro-kinks pile up against these obstacles in

contrast to smoothly curved bows for the Peierls model. Dislocation motion

by locking–unlocking is observed in some intermetallic materials. In Fe single

crystals, a transition occurs below about −20

◦

C from the double-kink mech-

anism to the locking-unlocking mechanism connected with a change in the

activation parameters [186].

4.5 Overcoming of Localized Obstacles

A way to increase the ﬂow stress of a material consists in alloying it with

foreign atoms. Depending on the concentration of the alloying element and

the respective phase diagram, the foreign atoms can either be solved in the

host lattice (substitutional or interstitial solutes) or they may precipitate as a

second phase. Usually, the interaction of these defects with the dislocations is

of short-range character. If the Peierls stress is low, the dislocation segments

bow out freely under stress, reaching an equilibrium conﬁguration as described

in Sect. 3.2.7. The way of overcoming the obstacles depends on the strength

and size of the latter. With respect to the size, the dimensions of the obsta-

cles parallel to the main direction along the dislocation line and in forward

direction have to be distinguished. Obstacles the dimension of which along

the dislocation line is not small compared to the mutual distance between

the obstacles are called extended obstacles. They will be treated in the fol-

lowing section. Obstacles pinning the dislocation only along a segment that

is short with respect to the distance are designated in this book as localized

obstacles. They may still have a ﬁnite size along the forward direction of the

dislocation motion. Extended and localized obstacles were illustrated above

in Fig. 3.20a, b.

102 4 Dislocation Motion

The problem of overcoming localized obstacles can be divided into two

parts:

The overcoming of individual obstacles

The statistical problem originating from a nonregular arrangement

obstacles on the glide plane

The process of surmounting the individual obstacles has been treated in

the foregoing sections, in particular in Sect. 4.1. In a regular arrangement,

the local eﬀective stress causes a force F = τ

∗

bl (4.2) on each obstacle. It

is opposed by an interaction force, which is described by the force–distance

curve introduced in Sect. 3.2.6. Since the localized obstacles are mostly small

with low interaction energies, their overcoming is supported by thermal

activation.

The statistical problem is mostly treated for a random arrangement of the

obstacles. Owing to the nonregular arrangement, the forces on the individual

obstacles are not equal and can be obtained from (3.48). To reduce the num-

ber of parameters, the relevant quantities can be normalized. A characteristic

length is the so-called square lattice distance l

,wherel

is the average area

of the slip plane per obstacle. Thus,

≈

√

. (4.48)

Here, c is the atomic concentration of the obstacles. The forces are normalized

using the line tension Γ

f = F/(2Γ ) (4.49)

and the obstacle strength

= F

/(2Γ ). (4.50)

For the approximation of constant line tension, f =cosφ,whereφ is half the

angle of attack. The normalized stress is given by



∗

2Γ

. (4.51)

Analytical solutions of the statistical problem are available for some sit-

uations of the athermal surmounting of the obstacle array. In this case, the

applied stress must be high enough so that the dislocation can overcome the

strongest conﬁguration in the array. It was shown by Schwarz and Labusch

[187] that the solutions depend on the relation between the extension x

the obstacle in x direction and its strength f

as described by the parameter

=(x

−1/2

. (4.52)

In the limit of ξ

 1, the obstacles have no extension and are called

point obstacles. All obstacles oppose the dislocation motion and the dislo-

cation bows out between them. This case was ﬁrst treated by Friedel [188],

4.5 Overcoming of Localized Obstacles 103

it is designated “Friedel” statistics. If ξ

 1, the dislocation is in touch

with obstacles on both the entrance and the exit sides of their force–distance

curves. Thus, the obstacles cause forces on the dislocation in the forward and

backward directions. The respective theories follow “Mott” statistics [189]. In

the following, both cases are described.

4.5.1 Friedel Statistics

As pointed out earlier, Friedel statistics is valid for small isolated obstacles

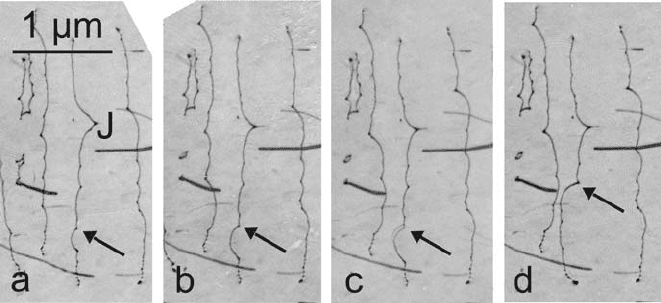
of relatively high strength. An example is given in Fig. 4.13. The obstacles

are small precipitates in an MgO single crystal. The dislocations form cusps

at the obstacles, resulting in forces acting on them. Owing to the nonregular

arrangement of the obstacles, the forces are not equal. Obstacles with a high

force, that is, an acute angle of attack, have a high probability to be quickly

surmounted. This is shown in the ﬁgure, where always the obstacles marked by

arrows are overcome. In Fig. 4.13c, the moving dislocation segment is imaged

twice due to its motion during the exposure of the ﬁlm. Thus, the advanced

dislocation segment spreads sidewise (upwards in the ﬁgure), similar to a kink

in the double-kink model. The jerky motion of the dislocations overcoming

localized obstacles is also presented in the Video 7.1. For simple geometrical

reasons, the average obstacle distance along the dislocation line is not equal

to the square lattice distance as observed by Friedel [188] and outlined in

Fig. 4.14. The ﬁgure presents two dislocation segments of length l in position

1, bowing out between three point obstacles to the equilibrium radius r.Ifthe

central obstacle is overcome, the dislocation moves to position 2 with the same

radius of curvature, sweeping the hatched area. According to Friedel statistics,

on average this area contains one additional obstacle, that is, it equals l

Fig. 4.13. Image sequence of dislocations in an MgO single crystal overcoming

localized obstacles during in situ deformation in an HVEM at room temperature.

Micrographs from the work in [190]

104 4 Dislocation Motion

Fig. 4.14. Geometrical representation of the Friedel relation between the average

segment length (obstacle distance) and the square lattice distance at overcoming

localized obstacles

With the approximations that the area of the segment of a circle is about

2/3 lh,withh being the height of the bowed segment, and

√

1 −  ≈ 1 − /2,

it follows for the average distance that

l =k

2/3

(2r)

1/3

(4.53)

or, with (3.38) r = Γ/(τb)=l

/(2τ



)

l =k

−1/3

. (4.54)

Consequently, the average obstacle distance depends on the stress. In gen-

eral,

l is greater than l

and approximates it for high stresses (τ



→ 1).

Considering the stress dependence of the obstacle distance in the equation of

the Gibbs free energy of activation (4.3) leads to the introduction of a numer-

ical factor of 3/2 into the relation for the experimental determination of the

activation volume (4.9), which then reads [191]

V =

. (4.55)

If the Friedel length is inserted into (4.2), the stress of the athermal

overcoming of a random array of obstacles of the strength F

becomes

3/2

√

2Γ

, (4.56)

or, in the dimensionless form,



3/2

. (4.57)

In the simple derivation according to Fig. 4.14, the numerical constants

and k

are equal to unity. The functional form of the Friedel relations

were checked ﬁrst by computer simulation [192] and later by both computer

4.5 Overcoming of Localized Obstacles 105

simulation [193–197] and analytical theories [198, 199]. These calculations

conﬁrm the Friedel relations and yield values close to unity for the numer-

ical constants. Suitable data are k

=0.73 [200] and k

=0.95 [199]. An

extension of the statistical theories including also inertia eﬀects of the dislo-

cations was given in [201]. These eﬀects become important only at very low

temperatures.

In addition to the macroscopic ﬂow stress at 0 K and the average obstacle

distance, the statistical theories yield information on the microscopic shape

of the moving dislocations. When a stress is applied to an originally straight

dislocation, it contacts a number of obstacles and bows out between them.

If no obstacle is surmounted, certain distributions of the obstacle distances

and forces on the obstacles result. These so-called starting distributions were

calculated in [202]. If the stress is increased successively, some obstacles will

be overcome, with the dislocation proceeding forward. After reaching a certain

threshold stress, the dislocation experiences its strongest conﬁguration, and

after a further increment of the stress it passes the remaining part of the

obstacle array. The strongest conﬁguration determines the athermal ﬂow stress

of (4.56). In this conﬁguration, both the obstacle distances and the forces

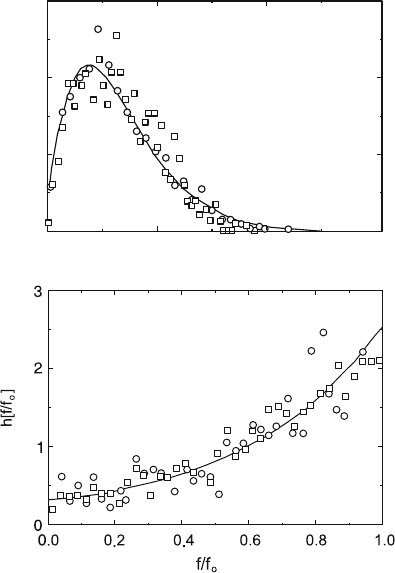
acting on the obstacles exhibit characteristic frequency distributions presented

in Fig. 4.15. The distribution of the segment lengths in Fig. 4.15a diﬀers from

the exponential distribution of points randomly arranged on a line, showing an

asymmetric maximum. In the force distribution of Fig. 4.15b, the frequencies

increase with increasing forces up to the maximum force f

. If the lengths are

expressed in units of 2f

r and the forces in units of f

, the curves can be

normalized as shown in the ﬁgure.

In a real material, the obstacles are usually not of equal strength. The

concentrations of obstacles of diﬀerent types α can be characterized by their

individual square lattice distances l

sqα

.Asinanarraycomposedofobstacles

of similar concentrations and strengths the concentrations add, there follows



sqα

For the simplest case of two types of obstacles of not very diﬀerent strength,

that is, stronger ones with α =s and weaker ones with α =w, the relative

fractions on the slip plane are

sqs

sqw

+ l

sqs

and x

sqw

+ l

sqs

Each type of obstacles produces an athermal ﬂow stress according to (4.57).

If small terms are neglected, the combined ﬂow stress is then [203]

2

= x

2

+ x

2

, (4.58)

or, in un-normalized form

= τ

+ τ

. (4.59)

106 4 Dislocation Motion

1.5

0.5

1.0

0.0

012 3

l/(2f

h[l/(2f

r)]

Fig. 4.15. Theoretical distribution of normalized obstacle distances and forces on

the obstacles. Curves: according to the analytical theory in [199]. Squares: according

to the numerical simulation in [198]

The composed average obstacle distance is given by

l = x

(τ



)+x

(τ



Here, the mean values

and

are not deﬁned by (4.54). This equation

presupposes that the stress is given by (4.57) and the respective strength f

0α

In a mixture of obstacles, however, the ﬂow stress is not equal to any of the

individual ﬂow stresses.

The relative concentrations of the obstacles of diﬀerent types along the

dislocation in the strength-determining conﬁguration do not correspond to

their fractions x

. As the composed ﬂow stress is high with respect to the

weak obstacles, the force acting on many of them is larger than their strength

(f>f

0α

) so that they are spontaneously overcome. The density of weak

obstacles is therefore lower than expected from their density on the slip plane.

For the cases treated in [203], a suﬃcient approximation of the concentration

of weak obstacles along the dislocation line is [204]

4.5 Overcoming of Localized Obstacles 107

= e

−3.14

)

−1.28

4.28x

The composed force distribution follows from the distribution h(f,τ



)for

a single type of obstacles at the stress τ



by the mixing rule

h(f)=h(f,τ



)



(f)

with the weight factors K

=1forf ≤ f

0α

and K

=0forf>f

0α

.An

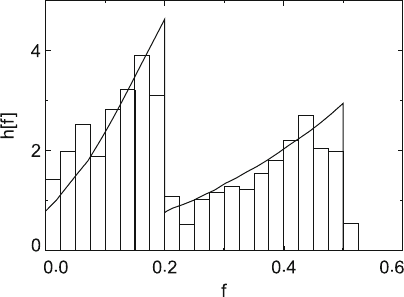
example is presented in Fig. 4.16 for f

=0.2andf

=0.5. The compos-

ite distribution abruptly decreases always at the strengths of the individual

obstacle types.

According to (4.57), for thermal activation the applied stress τ



is lower

than the athermal ﬂow stress. The statistical theories mostly consider a single

obstacle type only. It is assumed that the dislocation velocity is controlled by

the obstacles, which the highest force in the strongest conﬁguration is acted

on[194]. The waiting time at this obstacle is deﬁned by (4.6) and the simple

box potential ΔG =Δd(f

−f). This approximation is valid for high stresses

and low temperatures. In the opposite case, the probability of activation is

approximately equal at all obstacles. In computer experiments, the thermally

activated motion of dislocations was simulated using also other potentials, for

example, the Fleischer approximation [197]

ΔG =ΔG



1 − (f/f

)

1/2



(4.60)

following from (3.35). The eﬀect of the thermal activation on the conﬁguration

of the dislocation line primarily consists in the rapid overcoming of obstacles,

which are subject to high applied forces f/f

so that these obstacles disappear

Fig. 4.16. Composite force distribution for the athermal overcoming of obstacles of

strengths f

=0.2andf

=0.5. Curve: analytical theory. Histogram: computer

simulation. Data from [203]

108 4 Dislocation Motion

Fig. 4.17. Schematic representation of the eﬀect of thermal activation on the force

distribution. The force f

∗

is deﬁned by the applied stress via (4.61)

from the force distribution. In the range of small forces, the distribution is

aﬀected only little. This behavior results in a strong decrease of the frequencies

above a characteristic force f

∗

as indicated in Fig. 4.17. The force f

∗

correlates

with the applied stress by a Friedel relation analogous to (4.57)



∗

)

3/2

. (4.61)

The dislocation velocity in an array of obstacles of Fleischer type of

equal strength can well be represented by an activation energy resulting from

inserting the eﬀective force f

∗

from (4.61) into the Fleischer potential (4.60)

[197]

ΔG =ΔG



1 −



(τ



)

2/3



1/2



. (4.62)

The numerical factor of k

−2/3

=1.08 is close to that cited earlier. It is impor-

tant to note that the force f

∗

where the distribution breaks oﬀ enters (4.62)

and not the average force. The latter is essentially smaller than f

∗

Only at low stresses τ



/τ



, all obstacles have to be surmounted by ther-

mal activation. At higher stresses, part of the conﬁgurations is unstable with

f>f

. In this connection, the term “unzipping” is used as after a suc-

cessful activation at one obstacle, several neighbored obstacles are overcome

spontaneously. The dislocation motion becomes jerky on a mesoscopic scale.

The eﬀect does not depend on the temperature. The fraction j of conﬁgura-

tions that is overcome spontaneously is obtained from computer simulation.

In Fig. 4.18, it is plotted vs. the relative stress. The curve is represented by

the formula [201]

j =(τ



/τ



)

0.454

exp



−10.38 (1 − τ



/τ



)

3.78



4.5 Overcoming of Localized Obstacles 109

Fig. 4.18. Dependence of the fraction of unstable dislocation conﬁgurations during

thermally activated dislocation motion on the relative stress. Data from [201]

The fraction j is small up to about τ



=0.3 τ



where almost all obstacles have

to be overcome by thermal activation. At high stresses, almost all conﬁgura-

tions are surmounted spontaneously and the dislocation stops only at a few

very strong conﬁgurations so that its motion is most jerky and the character

is almost athermal.

In the case of thermal activation, the distributions of the obstacle distances

and forces depend not only on the stress τ



/τ



but also on the ratio between

ΔG

and kT. The limiting cases for low and high temperatures were calculated

in [205] by computer simulation. Accordingly, the segment length distribution

depends only little on the special conditions. It is always approximately equal

to the athermal case (Fig. 4.15a). In the limit of high temperatures, the typical

maximum (Figs. 4.15b and 4.17) disappears. After constant frequencies at low

forces, the distribution slowly tends to zero.

No comprehensive theory is available of the thermally activated surmount-

ing of an array of obstacles of diﬀerent strengths. It may be assumed that the

mixing rules for the athermal case of obstacles of similar concentrations and

strengths described earlier, in particular (4.58) and (4.59), are still valid. As

discussed by Kocks [206], other arguments apply to the thermally activated

surmounting of an array of many weak and a few strong obstacles like local-

ized obstacles and dislocations to be cut. These obstacles have to be overcome

simultaneously so that the Gibbs free energies ΔG of both processes have to

be equal. Instead of the quadratic superposition rule for similar obstacles, a

linear superposition rule should be used for both the stress components and

the reciprocal activation volumes,

∗

= τ

∗

+ τ

∗

(4.63)

. (4.64)