Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

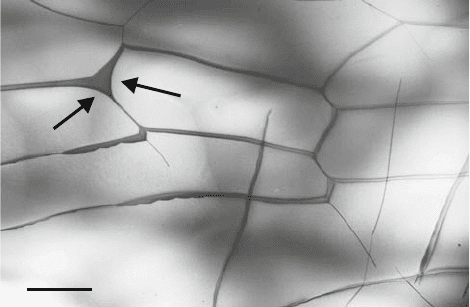
70 3 Properties of Dislocations

5 µm

Fig. 3.26. Dislocations in an SiC single crystal plastically deformed at 1700

◦

dissociated into Shockley partials. The viewing direction is [0001]. From the work in

[119]

The stacking faults cause a phase shift of the electron wave resulting in

an oscillatory diﬀraction contrast in the TEM depending on the height of the

fault in the specimen. The direction of R

can be determined by contrast

extinction in analogy to (2.9) for the Burgers vector. With respect to the

electron microscopy diﬀraction contrast, the displacement vector R

and the

shearing vector R are equivalent since, in general, both vectors diﬀer by a

translation vector of the lattice. The stacking faults in Fig. 3.26 are parallel to

the foil plane, thus showing a uniform area contrast. The dissociation width is

very large, owing to a very low stacking fault energy in the order of magnitude

of 2 mJ m

−2

. The stacking fault energy can also be determined from the radius

of curvature of the partial dislocations at extended dislocation nodes. Two

curved segments are indicated by arrows in Fig. 3.26. In this case, the bounding

force of the stacking fault is in equilibrium with the line tension of the bowed

partial dislocation. The dissociation of the dislocations essentially inﬂuences

their dynamic behavior so that it is important whether the dislocations have

a compact core, or are widely dissociated.

Stacking faults surrounded by a partial dislocation may also form by the

collapse of condensed vacancies, e.g., after quenching a crystal from high tem-

perature. In this case, the Burgers vector of the partial dislocation does not

lie on the fault plane. Thus, these dislocations cannot glide together with the

stacking fault. They are called Frank partial dislocations or Frank dislocation

loops [120].

3.3.3 Twins

Another way to produce a planar fault in the f.c.c. lattice is to mirror the

material on one side of a {111} plane, or to rotate it by 180

◦

. Then, the

stacking sequence ABC is changed into CBA, and the fault is called a twin.

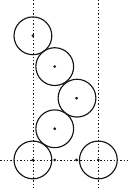
3.3 Dislocations in Crystals 71

Fig. 3.27. Stacking sequence at a twin in the f.c.c. lattice. The [

211] direction is

horizontal, the [111] direction is vertical

...ABCAB C BACBA ...

↑

The twin plane is labeled by the arrow. The view of the stacking sequence

corresponding to Fig. 3.24 is presented in Fig. 3.27. Twins can be formed in

small steps by the motion of partial dislocations on neighboring planes

... AB C AB C A B C ...

||||CABCA

|||||BCAB

||||||ABC

|||||||CA

||||||||B

The formation of twins is an alternative way to realize plastic deformation.

A twin lamella T in the intermetallic alloy TiAl will be shown in Fig. 9.8. The

series of partial dislocations creating the twin lamella are clearly visible. The

superdislocations S will be described in Sect. 9.3.

3.3.4 Antiphase Boundaries

Alloys consist of more than one type of atoms, e.g., atoms A and B. These

alloys may crystallize in an ordered structure like the ordered intermetal-

lic alloys. For example, the ordered alloy Ni

Al with the L1

structure is

based on the f.c.c. structure of the disordered phase. In the ordered state,

however, all atoms at the edges of the cube belong to one atom type (Al), and

all atoms in face centered positions belong to the other one (Ni). The Burgers

vector 1/2110 is a perfect Burgers vector in the disordered state but in the

ordered one, it connects an A atom with a B atom. Dislocations with such a

Burgers vector are called superpartial dislocations. The perfect Burgers vec-

tor in this direction of the superdislocation is therefore 110. Figure 3.28

presents a piece of a crystal consisting of a primitive lattice of A atoms on the

left side and an ordered region of A and B atoms on the right one. A perfect

72 3 Properties of Dislocations

APB SP

Fig. 3.28. Schematic of a dislocation having moved in an ordered region as a

superpartial dislocation forming an antiphase boundary

dislocation in the primitive lattice has moved to the right into the ordered

region. There, it has become a superpartial dislocation SP changing A atoms

into B positions. While in the regular ordered structure, atoms are always

neighbored by unlike atoms, now in the wake of the superpartial dislocation

like atoms are in nearest neighbor positions. This is a fault called antiphase

boundary or APB. Antiphase boundaries are two-dimensional faults like the

stacking faults. In this case, the displacement vector R

is a lattice vector in

the disordered structure, but not in the ordered one. In the latter, superdis-

locations frequently split into superpartials enclosing an antiphase boundary.

Their width is controlled similarly to that of partial dislocations enclosing

a stacking fault. The splitting of dislocations into superpartial dislocations

essentially inﬂuences the properties of dislocations in ordered intermetallic

alloys (Chap. 9).

Dislocation Motion

The character of the dislocation motion and the relation between the average

velocity and the applied stress are controlled by the interplay between the

forces on the dislocation segments, which vary in space and time, and the

spectrum of barriers to the dislocation motion. The barriers are very diﬀerent

with respect to their geometric extension and to their interaction strength,

ranging from arrangements of other dislocations with long-range stress ﬁelds

to individual foreign atoms, which interact with the moving dislocations only

in a very limited range. The character of overcoming these obstacles depends

on the total energy necessary to surmount the obstacles and their local exten-

sion as well as on the external parameters like stress and temperature. If the

energy is smaller than about 40kT,wherek is Boltzmann’s constant and T

the absolute temperature, and if the number of participating atoms is smaller

than a few hundred so that collective vibrations are possible, the overcoming

can be supported by thermal activation. In this case, the process strongly

depends on the temperature. In the other case, the whole energy has to be

expended by the external stress. Then, the parameters depend only weakly

on the temperature.

In the following, thermal activation is described by the example of a dis-

location segment locally pinned as in Fig. 3.20b. However, this process is far

more general and plays a role in almost all situations of dislocation motion.

Afterwards, the motion of a dislocation in the intrinsic periodic ﬁeld of the

crystal lattice is treated followed by the diﬀerent kinds of obstacles to disloca-

tion motion from single foreign atoms over precipitates to other dislocations.

So far, the obstacles are regarded as ﬁxed in the crystal. At high temperatures,

dislocation motion is inﬂuenced by diﬀusion. Self-diﬀusion processes under

the external stress or chemical stresses from nonequilibrium concentrations of

point defects may cause the dislocations to climb. Foreign atoms may segregate

to the dislocation cores and move with them. Finally, dislocation mobility laws

will be discussed, which are applicable to sets of phenomenological equations

describing plastic deformation.

74 4 Dislocation Motion

4.1 Thermally Activated Overcoming of Barriers

The theory of the thermally activated overcoming of obstacles to dislocation

motion was based on the thermodynamic treatment of viscous ﬂow by Eyring

[121]. A correct thermodynamic formulation was given by Schoeck [122]. The

basic formulae are demonstrated here for the case of the interaction between

gliding dislocations and localized obstacles, as described in Sect. 3.2.6, and

are therefore formulated in terms of shear stresses τ and shear strain rates ˙γ.

They can, however, analogously be applied to other situations of loading like

normal stresses at problems of climb.

Figure 3.20b shows that a gliding dislocation bows out under the action of

a shear stress between the obstacles resulting in a force on them, for small bow-

outs given by (3.48). In general, the force a bowed-out dislocation segment

of length l exerts is found by a work argument. If the point of action of the

dislocation on the obstacle is shifted forward by dx,wherex is the coordinate

in forward direction, the work done is F dx. At the same time, the dislocation

segment of length l is also shifted forward, supported by the external stress

∗

.The

∗

indicates that an “eﬀective” locally acting stress is meant. It will

be discussed in Sect. 5.2 that

∗

= τ − τ

, (4.1)

where τ is the applied shear stress and τ

is a long-range internal stress. The

gain in energy from the acting stress is

dW = τ

∗

bl dx = F dx,

which equals the energy spent on the obstacle. Thus, the force on the obstacle

F = τ

∗

bl, (4.2)

independent of the strength and conﬁguration of the bow-outs. If the force

on the obstacle is continuously increased, the point of attack will be shifted

as described by the force–distance curve of Fig. 4.1. This curve describes the

elastic response to the force acting. For a certain value of F , the dislocation

is in equilibrium at the position x

on the entrance side of the obstacle. If

the force reaches the maximum value of F , the obstacle strength F

max

,the

obstacle is spontaneously surmounted by the action of the stress τ

∗

.This

situation holds at temperature T = 0 K. At all lower forces or stresses, the

dislocation rests in elastic equilibrium at x

and can surmount the obstacle

only by the aid of thermal activation. If this happens, the dislocation reaches

the position x

on the exit side and is then free to move to the next obstacle.

The equilibrium positions x

(stable) and x

(unstable) depend on the acting

force. The (Helmholtz) free energy ΔF necessary to overcome the obstacle

at the actual force F is the integral over the force–distance curve from x

4.1 Thermally Activated Overcoming of Barriers 75

F(x)

ΔW

Δd

ΔG

max

Fig. 4.1. Force–distance curve during the overcoming of a localized obstacle

. (The free energy ΔF should not be mixed up with the force F .) Like the

dislocation moves under the external force F ,theworkΔW =(x

− x

)F is

gained from the external force or stress. This work corresponds to the rectangle

below the curve and is called the work term. The remaining part ΔG has to

be supplied by thermal activation. It is the Gibbs free energy of activation

for processes at constant pressure and temperature, and corresponds to the

hatched area in the ﬁgure. Thus,

ΔG =



F (x)dx − (x

− x

)F,

=ΔF (F ) − ΔdF,

=ΔF (τ

∗

) − Δdlb τ

∗

=ΔF (τ

∗

) − Vτ

∗

. (4.3)

The quantity Δd is an eﬀective depth of the obstacle, which is called

the activation distance. Frequently, the force–distance curve is expressed as

F (Δd), for example, in (3.35) for the Fleischer-type interaction between dis-

locations and defects with a tetragonal stress ﬁeld. The area Δdl is the

activation area. It is the area swept by the dislocation during the activation

event. Finally,

V =Δdlb =ΔAb (4.4)

is the activation volume. Independent of the microscopic interpretation of the

introduced activation parameters of surmounting localized obstacles, these

quantities have a well-deﬁned thermodynamic meaning, valid also for other

processes. The thermodynamic deﬁnition of the activation volume is

V = −

∂ΔG

∂τ

∗

. (4.5)

This is true although the integration limits and ΔF in (4.3) depend on the

force or stress. The Gibbs free energy of activation determines the rate of

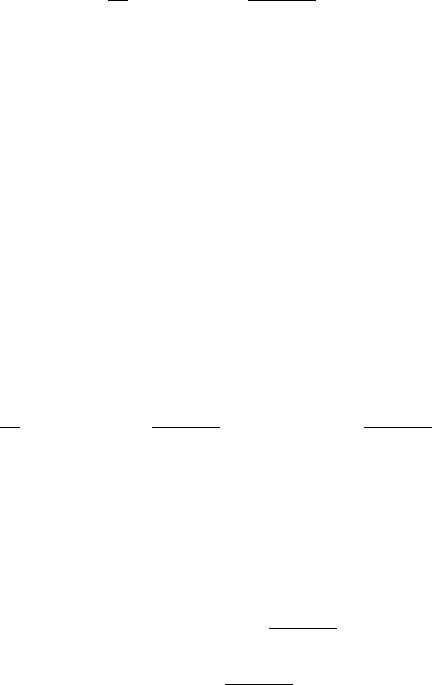
76 4 Dislocation Motion

overcoming the barriers by a Boltzmann factor

= ν

exp



−

ΔG(τ

∗

)



, (4.6)

where t

is the average waiting time of the dislocation at the obstacles before

their thermally activated overcoming, and ν

is an attempt frequency. Con-

sidering that the dislocation acts as a vibrating string, the attempt frequency

depends on the vibrating segment length l as [123]

= bν

/l.

Here, ν

is the Debye frequency of about 10

−1

. A more sophisticated

treatment was given in [124] yielding typically

≈< 10

−1

For a more detailed discussion see [9]. To obtain the dislocation velocity, the

activation rate of (4.6) has to be multiplied by the distance λ of forward

motion after successful activation. Accordingly,

= λν

exp



−

ΔG(τ

∗

)



= v

exp



−

ΔG(τ

∗

)



. (4.7)

This is the Arrhenius equation of the dislocation velocity. For the consid-

ered array of localized obstacles, the jump distance λ is approximately equal

to the obstacle distance or segment length l. Combining (4.7) with the Orowan

equation for the strain rate (3.5) yields the Arrhenius equation of the strain

rate

˙γ = b

λν

exp



−

ΔG(τ

∗

)



=˙γ

exp



−

ΔG(τ

∗

)



. (4.8)

˙γ

is the pre-exponential factor combining the parameters in front of the

exponential function.

Arrhenius relations are applied to many problems of dislocation dynamics.

The thermodynamic meaning of the activation parameters ΔF ,ΔG,andV

is always the same, whereas the microscopic structural interpretation of, for

example, the activation volume as V =Δdlb is valid only for the model of

overcoming localized obstacles. The latter is further developed in Sect. 4.5

considering the statistical problems related to the nonregular arrangement of

the obstacles.

The activation parameters can be measured by macroscopic deformation

tests. The experimental techniques are reviewed in Sect. 2.1, pointing out that

the most convenient methods are diﬀerential tests with instantaneous changes

4.1 Thermally Activated Overcoming of Barriers 77

of the deformation parameters and/or stress relaxation tests. The relation

between the (normal) stress σ measured in the tests and the resolved shear

stress used above is given by the Schmid relation τ = m

σ (2.3) with the

orientation factor m

. For the instantaneous changes, the internal stress τ

considered to remain constant so that the applied stress changes are equal

to the changes of the locally acting stress, ∂τ = ∂τ

∗

. These relations will be

discussed in Sect. 5.2.2. Diﬀerentiating (4.8) with respect to τ and taking (2.8)

into account yields the activation volume

∂ ln( ˙γ/˙γ

)

∂τ



T =const

= −

∂ΔG

∂τ

∗



, (4.9)

where r is the strain rate sensitivity. Considering the diﬀerentiation rules for

integrals shows that this relation is valid although ΔF and the integration

limits in (4.3) depend on τ

∗

or τ, respectively.

Frequently, the so-called stress exponent m is used to characterize the

dynamic dislocation behavior. It is based on a phenomenological power law

relation between the eﬀective stress and the strain rate

=const× τ

∗

or ˙γ =const× τ

∗

. (4.10)

Thus,

m =

∂ ln v

∂ ln τ

∗

∂ ln ˙γ

∂ ln τ

∗

∂ ln ˙γ

∂τ

∗

Vτ

∗

. (4.11)

The ﬁrst equality sign is valid only if the preexponential factor ˙γ

remains

constant during the measurement. The work term Vτ

∗

is the work by which

the activation energy is reduced owing to the action of the stress. As usu-

ally τ

∗

= τ, the true stress exponent m has to be distinguished from the

experimental one



∂ ln ˙γ

∂ ln τ

. (4.12)

In contrast to the activation volume, the relevant energy parameters are

not obtained directly. Diﬀerentiating (4.8) with respect to T leads to

∂ ln( ˙γ/˙γ

)

∂T



= −

∂ΔG

∂T



ΔG

= kT

∂ ln( ˙γ/˙γ

)

∂T



=ΔG + T ΔS =ΔH, (4.13)

since ∂ΔG/∂T = −ΔS is the activation entropy. Thus, the experimental

activation energy Q

, which is obtained from a temperature change test in a

creep experiment with constant stress, equals the activation enthalpy ΔH.In

a quasistatic test with constant strain rate,

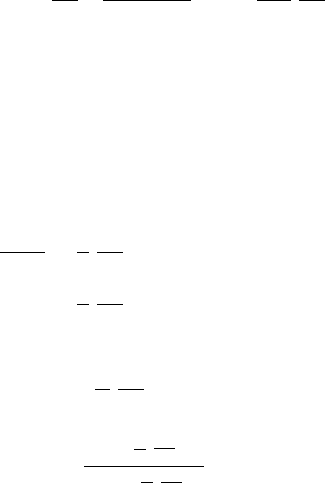
78 4 Dislocation Motion

=ΔH = −kT

∂τ

∂T



˙γ

∂ ln( ˙γ/˙γ

)

∂τ



= −

∂σ

∂T



˙γ

. (4.14)

The contributions to the activation entropy arise mainly from the fact

that all elastic interactions, that is, both the long-range interactions causing

as well as the short-range interactions determining the activation energy,

are proportional to a relevant elastic constant (mostly the shear modulus μ),

which depends on the temperature. If this is taken into account in (4.3) and

it is considered that the derivatives of the integration limits are zero because

of the equilibrium, it follows that

∂ΔG

∂T

∂μ

∂T

(ΔF + τ

V )

∂μ

∂T

(ΔG + τV) .

Thus,

=ΔG −

∂μ

∂T

(ΔG + τV)

ΔG =

∂μ

∂T

τV

1 −

∂μ

∂T

. (4.15)

This equation, derived by Schoeck [122], contains only measurable quan-

tities, not, e.g., τ

∗

.As∂μ/∂T < 0, it follows that the Gibbs free energy is

smaller than the experimental one, ΔG<Q

. To determine the interaction

potential of a special process controlling the dislocation mobility, it is neces-

sary to measure V and ΔG over a range of the stress τ as wide as possible. This

can be done by selecting wide ranges of the strain rate ˙γ and the temperature

T . However, it is then mostly questionable whether the preexponential factor

˙γ

remains constant as supposed in the derivations of the formulae. According

to (4.8), ΔG describes the preexponential factor for certain values of ˙γ and T .

At constant ˙γ,ΔG should be proportional to T . This may be used as a test

on the constancy of ˙γ

and the dominance of a single process controlling the

dislocation motion. As will be shown later, the diﬀerent mechanisms imply

diﬀerent values of the activation volume and the activation energies. Thus,

measuring these parameters may help identify the mechanisms of dislocation

mobility.

4.2 Lattice Friction

Owing to the periodic lattice potential, a dislocation moving in a crystal expe-

riences an intrinsic friction stress. As outlined in Fig. 4.2a, without external

stress, an edge dislocation is in a symmetric conﬁguration with the mini-

mum energy W

. When the dislocation moves in x direction, the conﬁguration

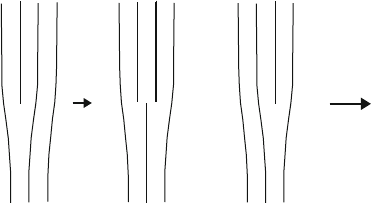
4.2 Lattice Friction 79

W(x)

(a) (c)(b)

Fig. 4.2. Shifting a dislocation through the lattice with two symmetric

conﬁgurations

becomes asymmetric. Accordingly, the energy increases and is a function of

the dislocation position. To increase the dislocation energy requires a stress.

In the middle of the way to the next equivalent minimum energy position,

at a distance of the Burgers vector b, another symmetric position occurs,

as sketched in Fig. 4.2b. Finally, the dislocation reaches the next minimum

energy position as in Fig. 4.2c.

Thus, in a crystal, a straight dislocation moves in a periodic lattice poten-

tial, which causes a frictional stress. This stress is called the Peierls–Nabarro

stress. However, if a straight dislocation moves from one minimum energy

position, a so-called Peierls valley, to the next one as a whole, many bonds

have to be broken and restored simultaneously, still requiring a relatively high

energy. This energy can be expended at small steps by the sidewise motion

of kinks. Starting with a straight dislocation, as a ﬁrst step, a kink pair has

to be formed, which requires the kink pair formation energy. Afterwards, the

kinks of opposite sign of the pair spread in opposite directions slowly shifting

the whole dislocation to the next Peierls valley. As the kinks also move in

a periodic lattice potential, each step of motion needs a respective energy.

Up to this point, the necessary energy was supplied by the acting mechanical

stress. However, the kink formation and migration energies are usually not

very high. Besides, only a small number of atoms is involved in an elemen-

tary step of the kink motion. Consequently, the kink formation and migration

can be supported by thermal activation, resulting in a strongly temperature-

dependent friction stress. In the following, these processes will be outlined

mainly following the detailed treatment in [12].

4.2.1 Peierls–Nabarro Model

To model the motion of a straight dislocation in the periodic lattice poten-

tial, Dehlinger and Kochend¨orfer [125] suggested to apply the calculations of

Frenkel and Kontorova [126] of a one-dimensional array of balls connected