Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

40 3 Properties of Dislocations

In order to obtain the strain rate ˙γ, (3.4) has to be diﬀerentiated with

respect to the time t,˙γ =dγ/dt. In general, both the dislocation density

 and the displacement λ may depend on time. Mostly, a limiting case is

considered where a certain density of mobile dislocations 

changes slowly

in time, so that only the change of the dislocation displacement is considered,

i.e.,

˙γ = b

dλ

= b

, (3.5)

where v

is the dislocation velocity. This is the well-known Orowan relation

between the plastic strain rate, the dislocation density, and velocity [77]. The

dislocation velocities range from fractions of nanometers per second to a limit-

ing velocity, which is related to the velocity of sound. The processes controlling

the dislocation velocity are the topic of this book.

Another limiting case occurs if dislocations are created at a source,

move successively very quickly over a certain distance λ and are afterward

annihilated or immobilized. Then,

˙γ = bλ

d

= bλ ˙.

In general, both λ and  will depend on time, but the slow changes of  are

mostly neglected so that (3.5) can be applied.

3.2 Elastic Properties of Dislocations

The elastic strains around a dislocation result in an elastic stress ﬁeld. This

ﬁeld reacts with the stresses originating from the external stress acting on the

body, and with the stress ﬁelds of all the other crystal defects. This results in

forces along the dislocation line which drive the dislocation at some segments

and impede it at others.

In elasticity theory, stresses and elastic strains are tensors. Their compo-

nents are denominated σ

and ε

. Most of the formulae given in this book

refer to linear isotropic elasticity. Then, i, j =1, 2, 3 refer to the three coor-

dinate axes x

. Stress or strain components with i = j are normal stresses

or strains. Those with i = j are shear stresses or strains. In Sect. 3.2.7, the

inﬂuence of anisotropy on the line tension of dislocations will be discussed.

The strain components are derived from the elastic displacements u

in the

directions x

according to



∂u

∂x

∂u

∂x



. (3.6)

Thus, the deﬁnition of shear strain components is diﬀerent from the technical

shear strains introduced in Sect. 2.1 for the plastic shear strain

=2ε

i =j.

3.2 Elastic Properties of Dislocations 41

The symbols for stresses and strains are used in this book in the following

way: σ

and ε

represent the components of the stress and strain tensors

in formulae of elasticity theory, whereas σ denotes a tensile or compressive

stress and τ denotes a shear stress resolved on a particular slip system in other

chapters. The plastic tensile or compressive strains are denoted by ε and the

plastic shear strains by γ as introduced in Sect. 2.1.

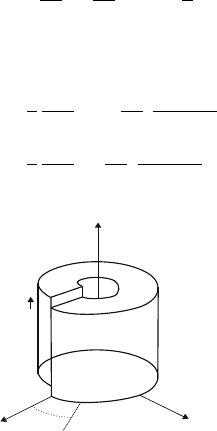
3.2.1 Stress Fields of Straight Dislocations

The stress ﬁelds of dislocations can be calculated by elastic straining of cylin-

ders according to the original treatment by Volterra [7]. As an example, the

model of a screw dislocation of inﬁnite length is presented in Fig. 3.7. The

three coordinate axes are denoted x, y,andz. The dislocation line extends

along the z axis. The unstrained cylinders are cut along a plane, and the

two faces of the cut are shifted with respect to each other by a constant dis-

placement, by the Burgers vector b. In the case of the screw dislocation, b is

parallel to the dislocation line, i.e., the z axis. Then, the faces of the cut are

glued together so that the body is intact again, but elastically strained. By

choosing a cylinder with a hole in its center, a singularity of the stresses at

the dislocation line itself is prevented.

It can be assumed that the displacements in x and y directions are zero,

and that the displacement in z direction increases linearly with the cylinder

coordinate angle ϕ

= u

ϕb

2π

arctan

. (3.7)

Equation (3.6) is used to turn from the displacements to the strains. All strains

are zero except

∂u

∂x

= −

4π

+ y

∂u

∂y

4π

+ y

. (3.8)

Fig. 3.7. Creation of a screw dislocation by the cut method in an elastically strained

cylinder

42 3 Properties of Dislocations

Using Hooke’s law for the relation between the shear strains and shear stresses

with the shear modulus μ

=2με

i =j (3.9)

yields the shear stress components

= −

μb

2π

+ y

= −

μb

2π

= −

μb

2π

sin ϕ

μb

2π

+ y

μb

2π

μb

2π

cos ϕ

. (3.10)

Turning to cylinder coordinates with r and ϕ instead of x and y reveals that

the stresses decay with the reciprocal value of the distance r from the dislo-

cation. This is the slowest decay of all crystal defects. Only the stress ﬁeld

of cracks decays more slowly (with 1/

√

r). Thus, dislocations are sources of

long-range internal stresses. These are proportional to the absolute value of

the Burgers vector b and the shear modulus μ.

For the edge dislocation, the shift of the cut faces has to be perpendicular

to the line direction of the dislocation, as outlined in Fig. 3.8. In this case, the

displacement in z direction is zero. The derivation of the strains and stresses is

more complicated, it is not given here. For this aim, the diﬀerential equation

of the Airy stress function has to be solved. The most general solution was

given by S. Timoshenko and J.N. Goodier [78].

The components of the stress ﬁeld of an edge dislocation along z with the

Burgers vector parallel to x are

μb

2π(1 − ν)

−y(3x

+ y

)

+ y

)

μb

2π(1 − ν)

y(x

− y

)

+ y

)

= ν(σ

+ σ

)

μb

2π(1 − ν)

x(x

− y

)

+ y

)

= σ

=0. (3.11)

Fig. 3.8. Creation of an edge dislocation by the cut method in an elastically strained

cylinder

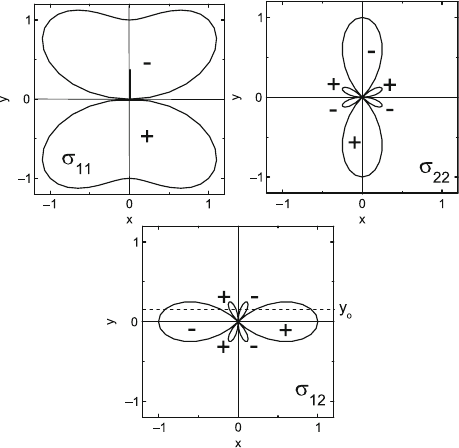
3.2 Elastic Properties of Dislocations 43

Fig. 3.9. Contours of equal stress σ

, σ

,andσ

of an edge dislocation in z

direction with the Burgers vector parallel to x. The coordinates are in units of

μb/(2π(1 − ν)σ

)

Here, ν is Poisson’s ratio. Figure 3.9 shows contours of equal stress of the edge

dislocation. Characteristic features are:

• The stress ﬁeld of the edge dislocation contains shear stress as well as

normal stress components.

• The stress ﬁeld does not show rotational symmetry as for the screw

dislocation.

• The stress ﬁeld is complementary (orthogonal) to that of the screw

dislocation.

• The shear stresses are zero in diagonal directions and perpendicular to the

Burgers vector, and

• The stress σ

equals σ

rotated by 90

◦

In order to calculate the stress ﬁeld of a mixed dislocation, the Burgers

vector is decomposed in its screw and edge components according to (3.2).

The stress ﬁelds of both components are superimposed linearly. Very often, the

dislocations are not straight. Curved dislocations will be treated in Sect. 3.2.7.

3.2.2 Dislocation Energy

The incorporation of a dislocation into a solid increases the free energy of

the latter mainly owing to the elastic stress ﬁeld. The additional energy is

44 3 Properties of Dislocations

attributed to the defect. The energy of the screw dislocation in a cylinder, as

it is introduced in the preceding section, can be calculated using elementary

means. The increase of the elastic energy in an elementary volume is given by

dE =



dV, (3.12)

where the sum has to be taken over all components of the strain and stress

tensors. Considering that for the screw dislocation all normal stresses are zero

and using (3.9), (3.12) reduces to

dE =

2μ

(σ

+ σ

)dV.

Inserting the stress components of the screw dislocation in cylinder coordi-

nates from (3.10 ﬀ.) leads to the energy increase

μb

8π

(cos

ϕ +sin

ϕ)rdrdϕdz.

The integration over the volume of the cylinder yields

μb

4π

where L is the length of the cylinder, i.e., of the dislocation. Usually, the

dislocation energy is expressed as the energy per length,

μb

4π

= E

. (3.13)

is the pre-logarithmic factor of the energy of the screw dislocation. The

respective formula for the edge dislocation is

μb

4π(1 − ν)

= E

. (3.14)

Thus, the energy of the edge dislocation is slightly higher than that of the

screw. For the mixed dislocation, the Burgers vector is decomposed again into

its screw and edge components according to (3.2). The total energy is the sum

of both parts

4π



1 − ν



μb

4π(1 − ν)



(1 − ν)cos

β +sin



μb

4π(1 − ν)

(1 − ν cos

β)ln

= E

. (3.15)

3.2 Elastic Properties of Dislocations 45

The radii r

and R are called the inner and outer cut-oﬀ radii. Their

deﬁnite values prevent the occurrence of singularities for both r

→ 0and

R →∞. The singularity for r

→ 0 results from the breakdown of linear

elasticity theory in the core of the dislocation. Therefore, the range where the

elasticity theory is not valid is cut oﬀ inside a certain radius and the energy

of the dislocation core is added to the total energy. A rough estimate of the

core energy is

μb

. (3.16)

Alternatively, r

can be chosen in such a way that the elastic energy rep-

resents the energy of both the linear elastic region around the dislocation plus

the energy of the dislocation core. r

is then called an “eﬀective” inner cut-oﬀ

radius. Its values are in the range of 0.3b<r

< 3b. For straight disloca-

tions, the outer cut-oﬀ radius R depends on the size of the crystal and of the

arrangement of the dislocations in it. For a single dislocation in the body like

the cylinder model in Fig. 3.7, R equals the dimension of the body. For a uni-

form arrangement of dislocations of opposite signs, the superimposing stress

ﬁelds screen each other so that R is equal to the mutual distance between

the dislocations. This is 1/

√

 if  is the dislocation density. Similarly, small

dislocation loops do not cause a long-range stress ﬁeld far from their place and

R = αD,whereD is the diameter of the loop and α<1. As a consequence,

the logarithmic term in the equations of the dislocation energy may take val-

ues between about 3 and 18. For a normal dislocation density of deformed

crystals in the order of magnitude of 10

−2

there follows R ≈ 3 × 10

−7

so that a rough estimate of the dislocation line energy is

μb

. (3.17)

The energy per lattice plane amounts to about 3 eV for usual data (b =

3 × 10

−10

mandμ = 30 GPa). Thus, the energy of even small dislocation

loops equals tens of electron volts so that the probability of their thermal

formation is practically zero.

In summary,

• the dislocation energy is proportional to the dislocation length

• the shear modulus and

• the square of the Burgers vector.

Due to the logarithmic factor, the dislocation energy also depends on

the arrangement of the dislocations. In crystals, the Burgers vector must be

a lattice vector which connects two equivalent lattice positions. Because of

the strong dependence of the dislocation energy on the Burgers vector, only

dislocations with the shortest possible Burgers vectors are stable.

If two dislocations of Burgers vectors b

and b

meet, they can react to

form a third one with b

if the reaction is associated with a gain in energy.

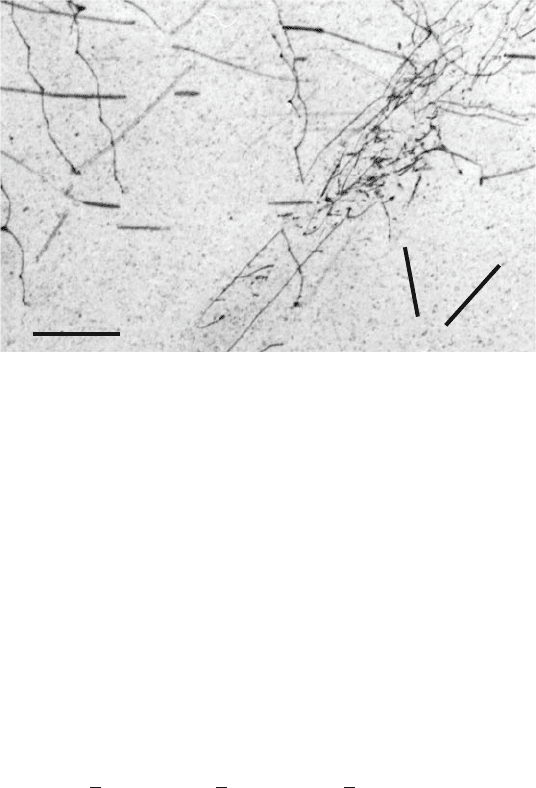
46 3 Properties of Dislocations

0.5 µm

Fig. 3.10. Intersection of two slip bands with diﬀerent Burgers vectors during in

situ deformation of an MgO single crystal in the HVEM at room temperature with

the creation of a dislocation junction marked by J. The viewing direction is turned

by about 15

◦

around [110] away from [001]. g = (010). Micrograph from [79]

Since the dislocation energy is proportional to the square of the Burgers

vector, the reaction will occur if

+ b

This is only a very rough estimate. For a more precise estimation, also the

character of the dislocations has to be considered. An example of a dislocation

reaction is presented in Fig. 3.10 where two dislocations on diﬀerent slip planes

meet to form a dislocation junction, i.e., a common segment which is not

glissile on the slip planes of the two original dislocations. In the NaCl structure

of the example in Fig. 3.10, the dislocations may react according to

[110](1

10) +

11](011) =

[101](10

1).

a is the lattice constant. The indexes in parentheses mark the respective slip

planes. It can easily be proven that the gain in energy is 50%. The original dis-

locations are labeled A and B. The dislocation junction J is only weakly visible

since it is extinguished at the (010) g vector. Dislocation junctions harden the

crystal if gliding dislocations intersect dislocations with other Burgers vectors.

This was ﬁrst discussed for f.c.c. crystals in [80]. In f.c.c. crystals, dislocations

may form so-called Lomer–Cottrell dislocations [81,82]. These dislocations are

thought to act as barriers blocking the motion of other dislocations. Then,

these dislocations pile up against the barriers forming long-range stress ﬁelds

as described in Sect. 5.2. The barrier strengths of several dislocation reaction

3.2 Elastic Properties of Dislocations 47

products are described in [83]. At high temperatures, dislocations can form

quite regular networks by dislocation reactions.

3.2.3 Forces on Dislocations

In general, a force F

acting along a coordinate η is deﬁned by the derivative

of the free energy with respect to η. In the special case where only mechanical

forces act, the free energy is replaced by the total mechanical energy W

yielding

∂W

= −F

∂η.

The total mechanical energy is composed of the elastic energy W

due to the

internal stresses, e.g., by the presence of dislocations, and the potential energy

pot

produced by the applied forces or stresses

= W

+ W

pot

Figure 3.11 shows a body of the dimensions L

, L

and L

,inwhicha

screw dislocation S has been introduced at x = 0 at the outer left surface

and is moved along a plane y = const supported by the external stress σ

into the position x near the outer right surface at L

. σ

is a shear stress in

the respective plane in z direction, which is also the direction of the Burgers

vector b. The total mechanical energy is then

μb

4π

− x

− L

γ. (3.18)

The left term is the elastic energy of the dislocation of length L

.Sincethe

dislocation in position x is near the surface at L

, the outer cut-oﬀ radius

R in (3.15) is suitably set equal to the distance between the dislocation and

the surface L

− x. The right term is the work done by an external force

in z direction F

= σ

shifted by a distance Δz = γL

. According to

Fig. 3.11. Screw dislocation near a surface of a body

48 3 Properties of Dislocations

Sect. 3.1.3, one dislocation moving from x =0tox produces a plastic strain

of γ = bx/(L

), leading to

μb

4π

− x

− L

bx.

The force in x direction is then

= −

∂W

∂x

= L



μb

4π(L

− x)

+ σ



. (3.19)

The force is proportional to the length L

of the dislocation. Usually, the

force per length f

= F/L is considered. The ﬁrst term in (3.19) represents

an attractive force in the direction to the nearest surface. It is also called an

image force as will be explained below. The second term is the force resulting

from the external shear stress. In simple terminology, this yields

= F/L = τb. (3.20)

This equation is the scalar version of the Peach–Koehler formula [84], where

is the glide force and τ the shear stress resolved on the respective slip

system.

The image force can be rationalized also by another argumentation. As a

simple case, Fig. 3.12 shows a screw dislocation D at a distance l to a surface.

The necessary boundary condition is that the forces perpendicular to the

surface are zero. In the coordinates of Fig. 3.12, this means that

This condition can be fulﬁlled by extending the body to the right and placing

another screw dislocation of opposite Burgers vector at the same distance l

outside the original body, the so-called image dislocation ID. According to

(3.10), the latter produces a stress

= −

μb

2π

+ y

μb

4πl

Fig. 3.12. Screw dislocation near a surface and its image dislocation

3.2 Elastic Properties of Dislocations 49

at the site of the original dislocation for x = −2l and y =0.Theminussign

considers the negative sign of the Burgers vector of the image dislocation.

This stress causes a force

= σ

b =

μb

4πl

, (3.21)

which corresponds to the ﬁrst term in (3.19).

As described in Sect. 2.4, image forces may limit the reliability of in situ

straining experiments in a TEM. This is especially true if the image forces

are of the same order of magnitude as the applied forces. In a typical in situ

experiment in the HVEM (shear modulus μ =30GPa,b =3× 10

−10

and specimen thickness 0.5 μm, i.e., l =0.1 μm), the image force amounts

to about 2 × 10

−3

−1

. This has to be compared with the Peach–Koehler

force from the applied stress. With a characteristic ﬂow stress of 200 MPa, i.e.,

a resolved shear stress of about 100 MPa, the Peach–Koehler force becomes

= σb ≈ 3 × 10

−2

−1

. Thus, the force from the applied load is more

than ten times higher than the image force, with the dislocation at a typical

distance to the surface. This relation will be worse for the thinner specimens

in conventional electron microscopy.

In its general form, the Peach–Koehler formula reads

=(b · Σ) × ξ. (3.22)

Σ is the stress tensor and ξ again the line vector of the dislocation. This force

can be decomposed into a glide component

[(b · Σ) ×ξ] · [ξ × (b × ξ)]

|b ×ξ|

andaclimbcomponent

[(b · Σ) × ξ] · (b × ξ)

|b × ξ|

. (3.23)

Here, b × ξ is the normal of the slip plane and ξ × (b ×ξ) is the normal of ξ

in the slip plane. Both force components are perpendicular to the dislocation

line.

On the basis of the force concept, it is possible to describe the interaction

of a moving dislocation with the external stress and the stress ﬁelds of all the

other crystal defects. The moving dislocation feels the sum of all stresses, i.e.,

the externally applied stress and the internal stresses of the defects. These

internal stresses can support or impede the action of the external stress. The

obstacle action controls the glide resistance of the moving dislocations. Thus,

the microscopic theory of the interaction between the moving dislocations and

other dislocations as well as with other crystal defects explains the properties

of the macroscopic plastic deformation. In this respect, it is necessary to dis-

tinguish between glide, cross glide, and climb motions. Accordingly, the force

components in the slip plane and perpendicular to it have to be calculated.

Some simple cases will be treated in the following section.