Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

60 3 Properties of Dislocations

x =

−1

τb

(E sin β − E



cos β)

y =

τb

(E cos β − E



sin β). (3.41)

For isotropic elasticity, the shape of the dislocation with its Burgers vector

parallel to x is an ellipsis with the major half axis E

/(τb)inx direction

(β =90

◦

) and the minor half axis (1 − ν)E

/(τb) perpendicular to it.

Comparing the shape of dislocations under load with the theoretical shape

oﬀers the opportunity to determine the stress acting locally on the bowed-out

dislocation segments. The ﬁrst measurement of this kind was performed in [99]

by ﬁtting circles to the electron micrographs of dislocations pinned under load

by neutron irradiation in order to determine the local radius of curvature. The

sizes of calculated shapes of dislocation loops under stress were matched to

long dislocation segments in [100] and elsewhere. Using this method, micro-

graphs of in situ straining experiments were studied in detail in [101, 102],

where the statistical data of pinned dislocations were also determined. All

these methods depended on a visual comparison between the micrographs

and the calculated dislocation shapes so that they are of subjective nature.

The ﬁrst attempt of a measurement independent of the observer was made

in [103] employing an image analyzer and curve ﬁtting techniques, analyzing,

however, only a few segments. In [104], a photometer head was moved by hand

over the micrographs projected in a high magniﬁcation, always in radial direc-

tion to ﬁnd points of equal brightness in both ﬂanks of the contrast proﬁle

of the dislocations. An example is shown in Fig. 3.19. The midpoint between

both points of the pairs was taken as the locus of the dislocation. This method

yields a constant accuracy independent of the orientation of the dislocation

in contrast to simply scanning the micrographs. The local radius of curvature

can be determined by polynomial regression analysis of second order over a

short segment. The center of this segment is then shifted along the dislocation

line to obtain the dependence of the radius of curvature on the orientation

angle.

In order to determine the locally acting stress from the dislocation curva-

ture, the line tension data are necessary. While the elastic constants are usually

known very precisely, the logarithmic factor of the dislocation energy (e.g., in

(3.15)) and thus of the line tension depends on the dislocation conﬁguration.

Hirth and Lothe [12] calculated the logarithmic factor of the dislocation energy

for some conﬁgurations by the method of piecewise straight dislocation seg-

ments. It turns out that if the self-stress of those parts of the dislocation

adjoining the segment under consideration are taken into account, the outer

cut-oﬀ radius has to be replaced by a length parameter l of the dislocation

conﬁguration. The logarithmic factor can be written as



+ C



. (3.42)

3.2 Elastic Properties of Dislocations 61

0.05 µm

Fig. 3.19. Negative copy of a dislocation segment taken during in situ deformation

of an MgO single crystal at high magniﬁcation with pairs of photometric measur-

ing points to determine the dislocation curvature. From [104]. Copyright Taylor &

Francis Ltd. (1985)

For a full hexagonal loop of the extension l Hirth and Lothe calculated the

value of C =1.16, for a semihexagon in a straight dislocation C = −0.59, and

for a so-called small bow-out of length l in a straight dislocation C = −2.39.

Thus, for a bowed-out dislocation segment, which is a very important con-

ﬁguration during dislocation motion, the logarithmic factor depends on the

length of the segment and on the strength of the bow-out. Since ln(l/r

) ≈ 6,

the dislocation energy may vary by a factor of two.

The numerical method introduced in [105] oﬀers an opportunity to deter-

mine the exact shape of a locally pinned dislocation. The dislocation is divided

into small segments. One circular segment at point P is selected. All the other

segments are considered straight. The segment at P is in equilibrium if the

applied stress τ equals the stress on the dislocation due to its own stress ﬁeld,

i.e., its self-stress τ

self

τ + τ

self

(P) = 0. (3.43)

All stresses are resolved onto the glide plane. The contributions of the self-

stress of all the other segments at P can be calculated by means of the Brown–

Indenbom–Orlov theorem [106–108]

self



sin(φ − ω)

|r|

+ E



)Δs. (3.44)

The sum has to be taken over all elements of length Δs. r is a vector pointing

from the element Δs to point P. φ and ω are the angles between a reference

orientation and r and the tangent vector at Δs, respectively. E

is the prelog-

arithmic factor of the energy of a straight dislocation lying along r, i.e., with

the line direction φ and not of the dislocation orientation β at P or at Δs but

having the Burgers vector of the dislocation. E



is the second derivative of E

62 3 Properties of Dislocations

with respect to φ. Equation (3.44) is valid for arbitrary anisotropic materials.

As for the line tension model, the properties of a curved dislocation are deter-

mined from the parameters of a straight dislocation of inﬁnite length. To ﬁnd

the equilibrium conﬁguration, point P is shifted along the dislocation, and

the sum of the external stress and the self-stress is minimized by a numerical

relaxation treatment. Equation (3.44) fails for the neighborhood of P itself

since the self-stress becomes inﬁnite. In [105], a piece of length 2r

around P

is cut oﬀ from the dislocation to avoid the singularity. This procedure diﬀers

from the original prescription by Brown [106] where the mean of two prin-

cipal values at both sides of the dislocation has to be taken. It was pointed

out in [109] that the cut-oﬀ method of [105] is incorrect, though it is used in

a number of papers. The choice of r

replaces the inner cut-oﬀ radius of the

dislocation energy.

A theoretical value for the numerical constant C for dislocations pinned

at impenetrable obstacles of a distance l can be obtained from the self-

stress calculations in [105]. This situation is shown in Fig. 3.20a. It is the

so-called Orowan process which will be describedinmoredetailinSect.4.7.

The dislocation bows out between large impenetrable obstacles of the same

elastic constants as the matrix, the diameter D and the inter-particle dis-

tance L. The authors compare the area ΔA (indicated in the right segment)

swept by the dislocation when the stress is increased from zero to an actual

value in the self-stress calculation with that obtained from the line tension

model. Both areas are equal if C = −1.61 is chosen. This is in the mid-

dle of Hirth and Lothe’s values for the semihexagon and the small bow-out,

(a)

ΔA

(c)

r = L/2

(b)

Fig. 3.20. Bow-outs of a dislocation. (a) Large bow-outs in a regular array of

extended impenetrable obstacles. (b) Small bow-outs at point obstacles. (c) Dislo-

cation segment of length L bowing out between two strong pinning points to the

critical conﬁguration with r = L/2

3.2 Elastic Properties of Dislocations 63

certainly being the best theoretical value. As mentioned earlier, both the line

tension and the self-stress calculations can be performed using dislocation

data from isotropic or anisotropic elasticity theory. The self-stress calcula-

tions are reﬁned in [110,111] by considering a possible orientation dependence

of the dislocation core energy. Problems with the core cut-oﬀ in calculating

the energy of dislocation loops are discussed in [112].

For small bow-outs of dislocations pinned in an array of small obstacles

as outlined in Fig. 3.20b, the constant C was experimentally determined from

the dependence of the dislocation curvature on the segment length in MgO

single crystals [104, 113]. From the local radius of curvature at a dislocation

orientation of β =0

◦

,10

◦

, or sometimes 25

◦

,themajorhalfaxese of the corre-

sponding ellipses were calculated by e = r(β) /



1+ν −3ν sin



. According

to (3.15), (3.38), (3.41), and (3.42), and Table 3.2, these values depend on the

segment length l as

e =

bτ

[ln(l/r

)+C]

= M[ln(l/r

)+C]. (3.45)

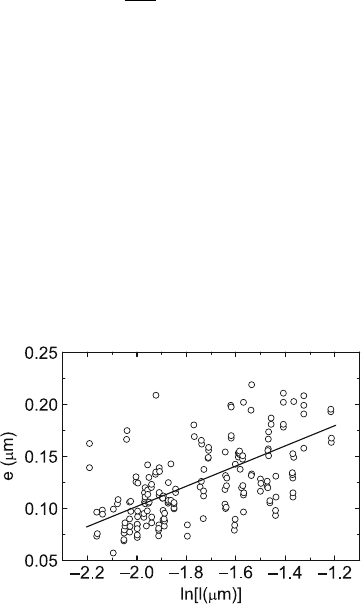
Figure 3.21 shows a respective plot of experimental data from a single elec-

tron micrograph. The large scatter of the data results from the diﬀerent local

conﬁgurations of the evaluated dislocation segments and from the variation of

the local eﬀective stress. Nevertheless, the positive correlation is clearly proved

statistically. Using the data of four similar micrographs and the eﬀective inner

cut-oﬀ radius of an edge dislocation in MgO of r

=0.4 b from the atomistic

calculations in [114], the intercept C equals −5.19 with 98% conﬁdence limits

of ±30%. Similar evaluations were performed for the precipitation hardened

alloys Al–4.5 wt% Zn–1.2% Mg and Al–8.36 at% Li [115], yielding the values of

C = −4.6andC = −5.6. Thus, the only available experimental data on the

Fig. 3.21. Dependence of the major half axes of bowed-out dislocation segments

on the logarithm of the segment length in an MgO single crystal during in situ

deformation in an HVEM. Data from [104]

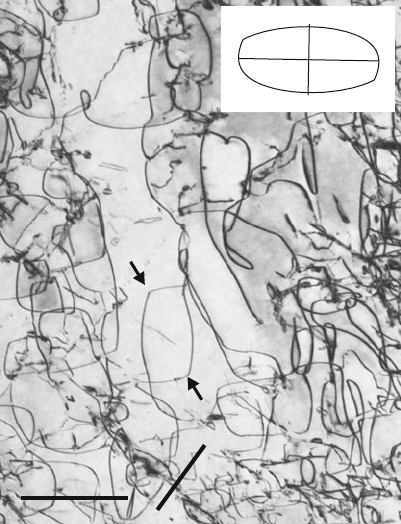
64 3 Properties of Dislocations

1 µm

Fig. 3.22. Dislocation structure in an Fe–43 at% Al single crystal deformed at

495

◦

C. The specimen is cut parallel to the (101) primary slip plane. g = (020) near

the [101] pole. Inset: elastic equilibrium shape of a dislocation with [11

1] Burgers

vector. From [8]. Copyright Elsevier (2005)

line tension are drastically lower than the theoretical values. The problem will

be followed further in Sect. 5.2.3.

In anisotropic crystals, frequently the line tension becomes negative in

certain ranges of the orientation angle β, which describes the dislocation

character. In these ranges, the dislocations are elastically unstable. An exam-

ple is given in Fig. 3.22. The inset shows the equilibrium shape of a closed

dislocation loop with its Burgers vector in horizontal direction calculated by

the line tension model using anisotropic elasticity data. Between about 38

◦

and 55

◦

the dislocations are unstable resulting in edges in the dislocation

line. In the micrograph, some edges are marked by arrows. At A, a mixed

dislocation is unstable and disintegrates into small segments. The regions of

elastic instability complicate the determination of the eﬀective stress from the

dislocation curvature.

A critical conﬁguration, in particular for processes of dislocation genera-

tion (Sect. 5.1.1), is the bowing of a dislocation segment between two strong

pinning agents. These may be nodes of a dislocation network or a change of

the dislocation line onto planes of high slip resistance, or large particles. In

3.3 Dislocations in Crystals 65

the simplest approximation, the line energy is constant according to (3.17),

independent of the dislocation orientation and the overall conﬁguration. Then,

the line tension equals the line energy, Γ = E, and the dislocation bow-outs

have a circular shape. As shown in Fig. 3.20c, while a segment of length L

bows out under stress, the half-circle with r = L/2 is the position of the

smallest radius of curvature. Using (3.38), it follows that

τb

≈

μb

2τ

, (3.46)

so that the half-circle conﬁguration is that requiring the highest stress τ

≈

μb

. (3.47)

This is the critical stress to fully bow out a dislocation segment. If it bows out

further, the radius of curvature increases again so that the segment becomes

unstable. The half-circle is the critical conﬁguration of the Frank–Read source

[116] described in Sect. 5.1.1.

In summary of this section:

• The line tension is a tangential force which considers the change in the

dislocation energy when changing the dislocation length and the orienta-

tion. For cusps in the dislocation line at relatively weak obstacles as in

the conﬁguration of Fig. 3.20b, the force on the obstacles is given by the

vector sum of the line tensions of the two adjacent segments

F =2Γ cos φ. (3.48)

φ is half the angle enclosing the neighboring segments.

• For strong bow-outs like the Orowan conﬁguration in Fig. 3.20a, the force

on the obstacles equals 2E (or better the energy of a dislocation dipole of

the respective width) and is thus not given by the line tension but by the

line energy.

• The line tension approximation neglects the dependence of the local dis-

location curvature on the overall dislocation conﬁguration. The actual

conﬁguration can be considered in the line tension model by choosing

appropriate values of the logarithmic factor in the dislocation energy.

• However, the only available experimental determination of the logarithmic

factor yields a considerably lower line tension than the theoretical values.

3.3 Dislocations in Crystals

In the earlier sections, dislocations were considered in an elastic continuum.

However, the discreteness of the crystal lattice and the particular crystal struc-

tures have a remarkable inﬂuence on the properties of the dislocations. Some

general aspects will be treated in the following sections. Particular situations

in speciﬁc materials like intermetallic alloys will be described in Part II of this

book.

66 3 Properties of Dislocations

3.3.1 Selection of Burgers Vectors

In the elastic continuum, dislocations can obtain Burgers vectors of arbitrary

length and orientation. However, in order to create a perfect dislocation in a

crystal, the Burgers vector has to be a lattice vector, i.e., it has to connect

equivalent lattice points. As expressed in (3.13)–(3.15), the energy of a dislo-

cation is proportional to the square of its Burgers vector. Thus, according to

Frank’s criterion [117] a dislocation of Burgers vector b can decompose into

two perfect dislocations with Burgers vectors b

and b

,if

+ b

. (3.49)

As a consequence, in most crystal structures only dislocations with Burgers

vectors corresponding to the shortest lattice vectors are energetically stable.

In particular, dislocations with Burgers vectors of multiples of perfect Burgers

vectors are unstable. Frank’s criterion neglects the inﬂuence of the orientation

angle β on the dislocation energy and eﬀects of elastic anisotropy. A more

exact stability criterion is therefore

E(b,β) >E(b

,β

)+E(b

,β

Although the orientation of the three dislocations in space is equal, the angles

β describing the dislocation characters are usually diﬀerent. Table 3.3 lists the

stable Burgers vectors in the most common crystal structures.

As it will be shown in Sect. 4.2.1, the lattice resistance to dislocation

motion is low for short Burgers vectors. Thus, dislocations with short Burgers

vectors have both a low defect energy and a low resistance to glide. In addi-

tion, the resistance stress is low for great atomic distances between the slip

planes. Such planes are the planes with small Miller indices. Some of these

dominating slip planes are also included in Table 3.3.

3.3.2 Stacking Faults and Partial Dislocations

Many metals crystallize in closed-packed structures. These structures can be

modeled by hard spheres, which are held together by attractive forces. Both

Table 3.3. Stable Burgers vectors and dominating slip planes in simple crystal

structures

Crystal structure Stable b Slip planes

f.c.c. 1/2110{111}

b.c.c. 1/2111, 100{112}, {110}, {123}

h.c.p. 1/211

20, 0001{0001}, {10

10}

Diamond cubic 1/2110{111}

NaCl 1/2110{110}, sometimes {100}

3.3 Dislocations in Crystals 67

1/2[–110]

1/2[–101]

[–211]

(111)

Fig. 3.23. Arrangement of atoms on a (111) plane in an f.c.c. crystal

(a)

(b)

Fig. 3.24. Stacking of closed-packed planes to form (a) f.c.c. and (b) h.c.p. crystal

structures. In (a), the [

211] direction is horizontal, the [111] direction is vertical

the f.c.c. and h.c.p. structures are based on the closed-packed plane outlined

in Fig. 3.23. It is a {111} plane in the f.c.c. lattice. The vertical position of

the atoms may be characterized by the center of the atom labeled A. For

a close packing, the next layer has to be positioned into the holes of the A

layer. The two vertical positions B and C closest to A are marked by dots. In

the notation of the ﬁgure, the positions are arranged along a [

211] direction.

Putting atoms into the holes B leads to a layer indicated by the two atoms

with broken lines. The structures formed by stacking A, B, C planes are closed

packed if two equal planes are not stacked on top of each other. As outlined

in Fig. 3.24, the f.c.c. lattice forms by the

...ABCABCABC ...

stacking sequence, and the h.c.p. lattice forms by the sequence

...ABABAB ... or ...BCBCBC ... or ...CACACA ...

In this lattice, the closed-packed plane is the {0001} plane. The {111} and

{0001} planes are preferred glide planes.

If the correct stacking sequence is interrupted, a planar fault is formed.

According to Frank [76], the fault is called an intrinsic stacking fault if the

68 3 Properties of Dislocations

normal stacking sequence is maintained on both sides of the fault. Such a fault

canbeformedbyremovingoneplanefrom the correct stacking sequence, e.g.,

...ABC|BCABC ...

In the other case of extrinsic stacking faults, an additional layer is introduced

into the normal stacking sequence

...ABCABC B ABCABC ...

The stacking faults can be characterized by the vector R

of the displace-

ment in the stacking sequence perpendicular to the fault plane. It is diﬃcult to

calculate the stacking fault energy since the bonds with the nearest neighbors

are not disturbed. For the same reason, the stacking fault energy is frequently

small.

Stacking faults can be formed by shearing. For example, the vector R =

1/6[

211] shifts a B plane into a C position. If all the material above that plane

is also shifted, an intrinsic fault results

...ABCA B C A B C ...

↓↓↓↓↓

CABCA...

This shift is produced by a dislocation, the 1/6[

211] Burgers vector of which

is not a lattice vector. Such dislocations are called partial dislocations. The

Burgers circuit cannot be performed completely in the perfect lattice. It is

therefore required that the Burgers circuit starts and ends on the fault plane,

as indicated in Fig. 3.25. A perfect dislocation can dissociate into partial

dislocations in the f.c.c. lattice by the reaction

[

101] =

[

211] +

[

12]. (3.50)

In the simple case, the energy balance of this reaction can be checked by

Frank’s criterion (3.49)

· 2 >

(6 + 6)

Thus, the dissociation is energetically favorable. Of course, the stacking

fault energy has to be considered. Neglecting the dependence of the disloca-

tion energy on its orientation, the dislocation can dissociate if, at the vector

addition of the Burgers vectors of the partial dislocations, there is an obtuse

angle between the two vector arrows. The reaction (3.50) is sketched in the

lower right corner of Fig. 3.23.

3.3 Dislocations in Crystals 69

A B

AAA

A B

A BA B

A B

AAA

Fig. 3.25. Intrinsic stacking fault ending at a partial dislocation with Burgers circuit

around the dislocation

The equilibrium width of the dissociated dislocation is obtained from the

minimum of the total energy of the dislocation. This includes the energy of

the two partial dislocations, the interaction energy between them and the

energy of the stacking fault. Increasing the width w of the stacking fault by

∂w increases its energy per length by γ

∂w,whereγ

is an energy per area.

Thus,

∂(energy per length)

∂w

= (attractive force per length)

on the bounding partial dislocation. This force is in equilibrium with the

repulsive elastic force between the partial dislocations. Considering that the

Burgers vectors of the partial dislocations are not parallel as in Sect. 3.2.4,

the relation between the energy of a stacking fault in the f.c.c. lattice and its

equilibrium width w

is given by

μb

8πw

2 − ν

1 − ν



1 −

2ν cos 2β

2 − ν



. (3.51)

Here, b

is the absolute value of the Burgers vector of the partial dislocations,

and β is the orientation angle between the total Burgers vector and the ori-

entation of the dislocation line. As a consequence, the equilibrium width of

edge dislocations (β =90

◦

) is larger than that of screws (β =0

◦

Partial dislocations created by the dissociation of a perfect dislocation

according to (3.50) are called Shockley partial dislocations [118]. The Burgers

vectors of the total dislocation and of both partial dislocations are situated on

the plane of the stacking fault. Thus, the whole dislocation can glide on this

plane. An example of such a dislocation dissociated into Shockley partials in

a hexagonal SiC single crystal is shown in Fig. 3.26. The dissociation reaction

is given by

[11

20] =

[01

10] +

[10

10].