Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

30 2 Experimental Methods

In analogy with the electrical circuit theory, this is also designated by Q

−1

Another measure is the logarithmic decrement δ. It is the natural logarithm

of two successive vibration amplitudes of the freely vibrating sample. Both

measures are related by

−1

ΔW

=2δ.

Internal friction measurements can be performed over a very wide range

of frequencies from less than 1 Hz up to the GHz range. The vibration modes

include bending, longitudinal, and torsional oscillations. At low frequencies,

an elongated (wire) specimen is excited by a torsion pendulum. Bending oscil-

lations can be obtained, for example, by suspending the specimen in the

vibration nodes on thin wires and exciting the vibrations by electrostatic

forces with the specimen or a thin metal ﬁlm on it being one electrode of a

capacitor with another ﬁxed electrode. At high frequencies, piezoelectric or

magnetostrictive transducers are used to excite the longitudinal oscillations.

At very high frequencies, the attenuation of sound waves is measured, which

travel from one transducer at one end of the specimen to another one at the

other end.

The energy losses in the solid are frequently due to thermally activated

relaxation phenomena between diﬀerent equilibrium positions of a crystal

defect with a waiting time t

for the transition given, for example, by (4.6) in

Sect. 4.1. Owing to a small bias due to the applied stress, the populations of

both positions change with the alternating stress. At low vibration frequen-

cies, the defects can easily follow the vibrations. At high frequencies, they

cannot follow at all. If the excitation frequency 2πω equals the relaxation fre-

quency t

−1

, there will be a damping maximum. Such measurements are also

called acoustic spectroscopy. The variation of the internal friction is a function

of the quantity ωt

−1

. Thus, the variation of the internal friction for obtain-

ing the friction maximum can either be achieved by varying the frequency

ω or by varying the relaxation rate t

−1

by changing the temperature. As in

the resonance mode the frequency is more or less ﬁxed, most internal friction

equipments allow measurements over a wide temperature range.

Part of the internal friction studies are devoted to the properties of point

defects (see the review in [56]). Anelastic eﬀects do not occur for defects that

can occupy only one position in the primitive cell or which can take two

centrosymmetric positions. Point defects that produce anelastic eﬀects may

be considered elastic dipoles, which reorient under stress. Such defects are,

for example, interstitials in body-centered cubic crystals. Their orientation

relaxation under stress causes the Snoek eﬀect [57–59]. The defect orientations

can also relax in the stress ﬁeld of dislocations producing the induced Snoek

eﬀect mentioned in Sect. 4.11. The quantities accessible by internal friction

measurements are the relaxation strength giving information on the concen-

tration of the defects and their anelastic strain contribution, the relaxation

time, and the orientation dependence. The latter yields information on the

symmetry of the defects.

2.5 Other Methods 31

Internal friction measurements are also used to investigate the properties

of dislocations. In materials in which the intrinsic lattice friction (the Peierls

mechanism, see Sect. 4.2) controls the dislocation motion, a Bordoni relax-

ation peak [60] is observed. The interpretation (e.g., [61]) is based on the

assumption of two energetically equivalent equilibrium positions of a dislo-

cation segment pinned at its ends with an acting internal stress. By means

of thermal activation, the segment can shuttle between these equivalent posi-

tions. From the superimposed alternating stress, a bias results with one of the

positions being more probable. If the excitation frequency equals the thermal

vibration frequency of the dislocation segment, a relaxation peak occurs.

In materials in which the lattice friction does not control the dislocation

mobility like in most metals under usual conditions, the pinned dislocation

segment is treated as an elastic string having a mass per length resulting in an

inertia, a line tension which keeps the segment taut, and the motion of which

is viscously damped. This results in an equation of motion given in (4.75) in

Sect. 4.9. This equation has to be solved under the actual boundary conditions.

The model originally suggested by Koehler [62] and developed by Granato

and L¨ucke [63] assumes that the dislocation segment is ﬁxed at its ends by

strong pinning agents like nodes in the dislocation network or precipitates,

and that it is pinned in between by further weak pinning points like solute

atoms or small precipitates. The pinning is described in detail in Sect. 4.5. At

small amplitudes where the dislocation segments do not detach from the weak

pinning points, the short segments vibrate and cause an internal friction peak

with a damping independent of the exciting amplitude. The frequency of the

maximum is usually in the range of tens of MHz, or higher. At frequencies

below the maximum, for the logarithmic decrement the theory yields

= α

μb

ωBL

, (2.10)

where α

is a constant considering the particular orientation relations and the

distribution function of the segment lengths L, μ is the shear modulus,  is the

dislocation density (Sect. 3.1.3), b is the absolute value of the Burgers vector

(Sect. 3.1.1), and B is the viscous damping constant in (4.74) in Sect. 4.9.

The damping maximum is connected with a change in Young’s modulus, the

so-called modulus defect,

ΔE

= α

μL

which causes a change in the resonant frequency. α

is another constant.

Figure 2.12 presents the temperature dependence of the square of the resonant

frequency and the internal friction of a niobium single crystal at low temper-

atures. Torsional oscillations at about 500 Hz were introduced by electrostatic

excitation.

In a comparative study, the segment length in deformed MgO single crys-

tals has been measured by both internal friction at diﬀerent temperatures

and in situ straining experiments in an HVEM [65]. For this aim, the quan-

tity δ

/(ΔE/E) has been calculated, which has the advantage that the (not

32 2 Experimental Methods

Fig. 2.12. Square of the resonant frequency (which is proportional to the respec-

tive modulus) (a) and internal friction (b) of a niobium single crystal at low

temperatures. The peak is due to lattice friction. Data from [64]

well known) dislocation density is eliminated. With all the uncertainties of

the internal friction method, the values of both techniques well agree.

With increasing vibration amplitude, the dislocation segments detach from

the weak pinning points, leading to an increase in the internal friction. This

amplitude dependent internal friction δ

is additive to the amplitude indepen-

dent internal friction δ

. The amplitude dependent internal friction should be

related to the macroscopic ﬂow stress at small strains in materials where the

ﬂow stress is controlled by the interaction between dislocations and point-like

obstacles, for example, foreign atoms or very small precipitates (Sect. 4.5). A

phenomenological relation between the decrement, the stress amplitude, the

strain rate at the stress amplitude, the frequency, and the stress exponent

((4.10) in Sect. 4.1) was derived in [66]. For an experimental test of the con-

nection between both methods, it is necessary to deﬁne a comparable stress

level. Diﬀerent criteria have been used. As shown in [67], the stress necessary

to reach a ﬁxed plastic strain due to dislocation motion is a suitable quantity,

which can be measured in both methods. The respective stresses then show

the same temperature dependence.

Internal friction measurements can be performed in situ during simulta-

neous elastic loading or quasistatic plastic deformation as reviewed in [68].

During active plastic deformation, the internal friction increases by both a

structural component δ

and a dynamic one δ

. The structural component

arises from the increase in the dislocation density  during deformation, which

occurs in (2.10). The dynamic component is explained by assuming that the

vibrational energy due to plastic deformation is proportional to the plastic

strain γ achieved during the time of one period 2π/ω,thusΔW

∝ ˙γ/ω,

where ˙γ is the plastic strain rate. The latter can be described by the Arrhe-

nius relation (4.8) and (4.3) in Sect. 4.1. Superimposing the constant applied

stress and the oscillating one and integrating over one period yields for the

dynamic damping

πMV ˙γ

ωkT

2.5 Other Methods 33

if the eﬀect of the oscillating stress on the strain rate is linearized. M is the

appropriate elastic modulus and V the activation volume. This is an amplitude

independent internal friction, which is proportional to the macroscopic strain

rate and inversely proportional to the oscillation frequency. If the linearization

is dropped, the friction becomes amplitude dependent.

Because of the nonlinearity of the Arrhenius relation, the superimposed

oscillating stress causes a softening eﬀect, the so-called acousto-plastic eﬀect,

which becomes evident either as an increase in the strain rate during creep

experiments (Archbutt eﬀect [69]) or as a decrease of the ﬂow stress in

quasistatic experiments (Blaha–Langenecker eﬀect [70]). In most materials,

the softening sets in when the oscillation amplitude reaches the amplitude

dependent range.

In conclusion, internal friction measurements are versatile methods to

study dynamic properties of dislocations, in particular the interaction with

localized obstacles.

2.5.4 Nuclear Magnetic Resonance

Nuclear magnetic resonance (NMR) is a complementary technique to study

the static dislocation structure as well as the dynamic behavior of dislo-

cations. In contrast to many other methods, NMR measurements are only

slightly inﬂuenced by the surface so that they register bulk properties. To per-

form dynamic measurements, the specimen chamber of a deformation machine

has to be ﬁtted between the pole pieces of the electro-magnet of the NMR

spectrometer. Most experiments are performed in the quasistatic mode at a

constant strain rate, which sometimes has to be quite high, that is, up to

10 s

−1

The methods are based on the interaction between nuclear electric

quadrupole moments and electric ﬁeld gradients of nuclei with a spin I>1/2.

In a cubically symmetric nuclear environment, there does not exist a static

electric ﬁeld gradient at the nucleus so that there will be no interaction. The

strain ﬁeld around a dislocation, however, destroys the symmetry resulting in

an interaction. The theory of the techniques is reviewed in [71].

Dislocation density measurements are carried out in ultra-pure crystals in

order to avoid lattice distortions by other defects. The quadrupole broadening

of the NMR signal is then proportional to the square root of the dislocation

density (e.g., [72]). For more detailed studies, the diﬀerence between edge

and screw dislocations and the arrangement of the dislocations on several slip

systems may be considered. Dislocation densities on diﬀerent slip planes can

be obtained from the orientation dependence, as shown in [73].

For studying dislocation dynamics by pulsed nuclear magnetic resonance,

the Orowan equation between the strain rate, the mobile dislocation density,

and the dislocation velocity (3.5) is considered assuming that the dislocation

motion is not continuous but jump-like. Then, the dislocation velocity is given

by v

= λ/t

,whereλ is the jump distance and t

the waiting time between

34 2 Experimental Methods

the jumps. Obstacles causing the jerky motion may be precipitates and, in

particular, forest dislocations. The motion of a dislocation is accompanied

by movements of the surrounding atoms, resulting in a nuclear spin-lattice

relaxation process with a relaxation time in a weak rotating ﬁeld t

1ρ

.This

parameter is the suited NMR parameter as its “time windows” are in the

range of t

. At suﬃciently high strain rates where 1/t

is large compared to

the Larmor frequency of the rotating frame, there is a relation between the

relaxation time and the strain rate ˙ε

1ρ

= A

˙ε

bλ

where b is the absolute value of the Burgers vector and A is a factor depending

on the nuclear magnetic properties of the dislocation, the mean local magnetic

ﬁeld in the rotating frame, and the weak rotating applied ﬁeld. These parame-

ters can be determined separately so that measurements of t

1ρ

yield the jump

distance λ. The experimental values are mostly compatible with the distances

between forest dislocations (e.g., [74]). More recent results on NaCl including

deformation-induced point defects are given in [75].

Properties of Dislocations

In order to understand dislocation dynamics, ﬁrst the geometric and elastic

properties of dislocations have to be treated. The geometric features decide on

the mode of dislocation motion. The elastic stress ﬁelds around the disloca-

tions interact with the applied stress and stress ﬁelds of all the other defects in

the crystal resulting in forces acting on the moving dislocations. These forces

drive or impede the dislocation motion.

3.1 Geometric Properties

3.1.1 Burgers Vector

The dislocation introduced in Sect. 1.2 is a special case of a general crystal

dislocation, the so-called edge dislocation ﬁrst described by Orowan, Polanyi,

and Taylor [3–5]. Such a dislocation in a primitive cubic model crystal is shown

again in Fig. 3.1a. The inserted extra half-plane is marked by full circles. The

edge dislocations are frequently symbolized by a T (in the present case rotated

by 180

◦

). The other special case is the screw dislocation introduced by Burgers

[6] and is shown in Fig. 3.1b. In contrast to the edge dislocation, the shift

vector or Burgers vector is now parallel to the dislocation line.

The Burgers vector b was introduced in Fig. 1.2 in a qualitative way. An

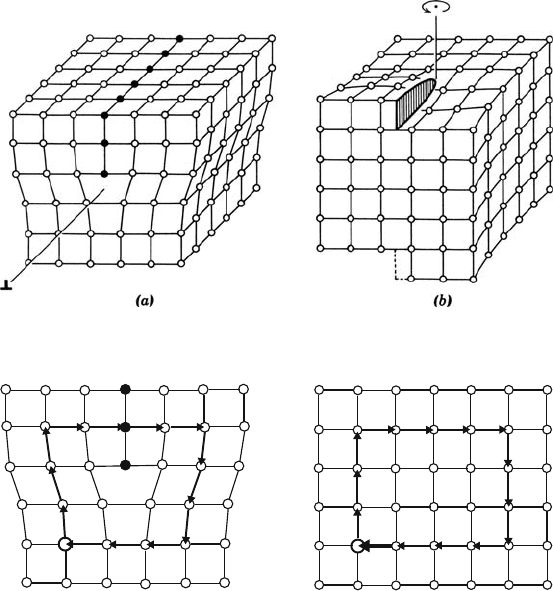
exact deﬁnition is obtained from the so-called Burgers circuit outlined in

Fig. 3.2 [6]. In this construction, the dislocation line is surrounded along a

closed path by a number of deﬁned steps as shown in Fig. 3.2a. The circuit

starts and ends at A. Afterwards exactly the same sequence of steps is repeated

in a perfect reference lattice demonstrated in Fig. 3.2b. Because of the pres-

ence of the dislocation in Fig. 3.2a, the circuit is not closed now. The vector of

the additional step necessary to close the circuit in the reference lattice is the

Burgers vector b. To establish its sign, the direction of the line vector ξ and

the sign of the circuit have to be considered. There exist diﬀerent conventions,

e.g., [76]. If the sign of the line vector is changed, the sign of the Burgers vec-

tor changes too. For a dislocation in a continuous medium, the Burgers circuit

36 3 Properties of Dislocations

Fig. 3.1. Models of an edge (a) and a screw dislocation (b) in a cubic primitive

lattice

(a) (b)

Fig. 3.2. Deﬁnition of the Burgers vector by the Burgers circuit

is replaced by a line integral over the displacements u along a closed curve C

around the dislocation loop. Thus, the Burgers vector is determined by

b =



du. (3.1)

The Burgers vector describes both the shift of one part of the crystal

with respect to the other along the face which was swept by the dislocation

causing a change of the shape of the body, and the strength of the elastic

strain ﬁeld around the dislocation. The character of the dislocation is deﬁned

by the angle β between the Burgers vector b and the line vector ξ of the

dislocation. As described earlier, β =90

◦

for an edge dislocation and β =0

◦

for a screw dislocation. For all the other angles, the dislocation is called a

mixed dislocation. Its Burgers vector may be decomposed into an edge and a

screw component according to

= b cos β, b

= b sin β. (3.2)

3.1 Geometric Properties 37

edge

screw

Fig. 3.3. Generation of a glide dislocation loop by shifting the faces adjoining an

internal cut against each other by the Burgers vector b

Fig. 3.4. Generation of additional crystal volume by the general motion of a

dislocation segment

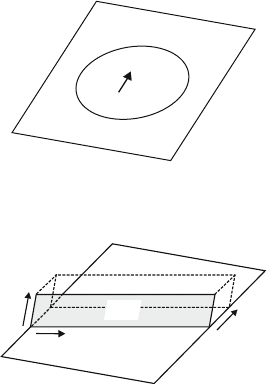
A dislocation loop with all characters can be generated by an internal cut

ending along a closed line and by shifting the faces adjoining the cut against

each other by the Burgers vector. For a glide loop, this is outlined in Fig. 3.3.

Those parts of the dislocation which are parallel to b have screw character,

those which are perpendicular to it are of edge character, whereas all the other

parts are mixed.

There are some laws of conservation of the Burgers vector. It is constant

along a dislocation line. If a line branches at a dislocation node, the sum of

the Burgers vectors of all branches is zero. Besides, a dislocation cannot end

inside a crystal, but only at a node, or an interior or exterior surface.

3.1.2 Glide and Climb Motion of a Dislocation

The dislocation motion can be accompanied by a change of the crystal volume.

The created volume depends on the directions and magnitudes of the Burgers

vector, the line vector, and the vector of displacement of the dislocation as

depicted in Fig. 3.4. The ﬁgure shows a plane containing the Burgers vector

b and a dislocation segment of length L and direction ξ. This segment may

move by a distance dx,sweepinganareada.Sincetheedgecomponentofthe

dislocation represents an incomplete extra lattice plane, its general motion

is connected with an extension or reduction of the size of this extra plane,

resulting in a change of the total crystal volume. As imaged in the ﬁgure, the

additional volume is given by the product of the three vectors as

dV =(b · da)=(b · (Lξ) × dx). (3.3)

38 3 Properties of Dislocations

The mode of dislocation motion is deﬁned by the process either being

conservative with respect to the crystal volume, i.e., dV = 0, or being non-

conservative, i.e., dV = 0. In the ﬁrst case, the motion is called glide or slip.

This is the dominating mode of dislocation motion in most materials and at

most temperatures. The nonconservative motion is called climb and is usually

connected with diﬀusion. Details of this mode will be described in Sect. 4.10.

As seen from (3.3), the volume production is zero if the dislocation moves

on a face containing the Burgers vector and the line vector. In particular, this

is a plane as shown in Fig. 3.4. This plane is called the glide or slip plane

of the dislocation. The glide plane is well deﬁned for the edge and mixed

dislocations. In an elastic continuum, for a screw dislocation with its Burgers

vector parallel to the dislocation line, all planes containing the dislocation line

are glide planes. In a crystal, however, only selected low-index crystallographic

planes may act as glide planes. Usually, the glide plane of the adjoining edge

part is attributed also to the screw segment of a dislocation. The motion is

called cross glide or cross slip, if the screw segment changes from this plane

to another glide plane.

In a real crystal, the place of a curved dislocation is not a smooth line,

owing to the discrete atomic structure of the material. The dislocation then

consists of straight segments parallel to crystallographic directions and transi-

tions between these straight segments. The transitions can be of atomic height

or may have the height of several atomic distances. If the transition parts are

situated within the slip plane, they are called kinks or superkinks depending

on their height. If the transition parts point out of the slip plane, they are

called jogs. Thus, jogs connect segments of the dislocation in diﬀerent slip

planes. Kinks and jogs are usual parts of the dislocation. Thus, the mode of

their motion is determined by the relation between the Burgers vector and

the line vector, as with any other part of the dislocation. Figure 3.5 shows a

dislocation loop with kinks K and jogs J. Since the kinks K extend within the

slip plane, they can glide together with the dislocation. It will be described

in Sect. 4.2.1 that the motion of the dislocations is realized by the formation

and sidewise spreading of the kinks. In contrast to that, the slip planes of

the jogs J (shaded areas) are not identical with the slip plane of the other

segments of the dislocation. The slip plane of a jog in the edge part E of the

dislocation loop extends perpendicular to the main course of the dislocation.

Thus, the jog can glide together with the dislocation if the dislocation loop is

enlarged by plastic deformation. However, the slip plane of a jog in the screw

part S of the loop extends parallel to the general course of the dislocation.

As a consequence, these jogs can glide along the dislocation but they cannot

glide in its forward direction. These jogs represent obstacles to the dislocation

motion. Their forward motion requires climb.

3.1 Geometric Properties 39

Fig. 3.5. Kinks K and jogs J in a dislocation loop with edge E and screw parts S

Fig. 3.6. Plastic shear strain produced by the motion of one dislocation across a

cube of an edge length L

3.1.3 Relation Between Dislocation Motion

and Plastic Strain and Strain Rate

The plastic strain obtained after the motion of dislocations depends on the

density of dislocations, their Burgers vector, and the distance these disloca-

tions move. Figure 3.6 shows the change of the shape of a cube of edge length L

after one dislocation has moved across the cube. The body has then a surface

step of length L and height b, and is sheared by the strain γ =tanϕ = b/L.

If n dislocations glide only over a fraction λ/L of the length of the body, the

strain is γ = nbλ/L

. Since the dislocation density is deﬁned by the dislocation

length per volume,  = nL/L

, the strain is

γ = bλ. (3.4)

This is the shear strain in a particular slip system. The plastic tensile strain

follows from (2.4). As an example, if dislocations of the density  =10

−2

and the absolute value of the Burgers vector of b =3×10

−10

mmoveovera

distance of λ =10

−4

m each, the resulting shear strain is γ =3×10

−2

=3%.