Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

120 4 Dislocation Motion

screw dislocation

edge dislocation

Fig. 4.26. Shape of the {110} cutting plane of an octahedral particle in the NaCl

structure with edges parallel to 110 directions. The outer border marks a plane

for a cut through the particle center, the hatched area is for a noncentral cut

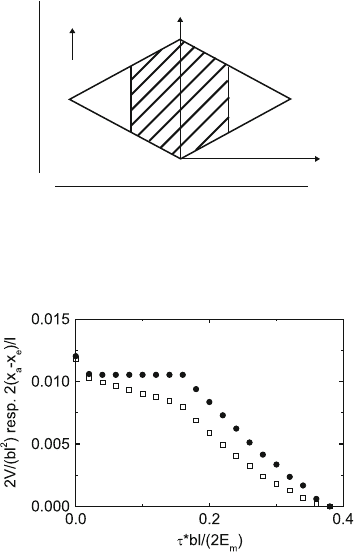
Fig. 4.27. Dependence of the normalized activation volume 2V/(bl

)(open squares)

and the normalized x diﬀerence 2 (x

− x

) /l (full circles) on the normalized stress

for the interaction between edge dislocations and particles with K

= K

=0,

bl/ (2E

) = 10, and E

=1.1. Data from [217]

volume is smaller than that following from the simple x diﬀerence. Thus,

the curves of stress vs. activation volume (force–distance curves) obtain a

narrow tip.

In particles with polygonal cutting planes, the dislocations can usually

assume equilibrium positions only within restricted ranges of stress. These

depend on x



and are diﬀerent on the entrance and exit sides. For the particles

of Fig. 4.27, stable positions are possible only for 0.16 ≤ τ

∗

bl/(2E

) ≤ 0.382

in the entrance half and for τ

∗

bl/(2E

) ≤ 0.023 in the exit half of the particle.

As long as τ

∗

bl/(2E

) < 0.16, the dislocation cannot enter the obstacle. It

is pinned at the tip and bows out in the matrix with increasing stress so

that z

= 0. Between τ

∗

bl/(2E

)=0.16 and 0.382, the dislocation enters

the particle and forms a stable equilibrium position with z

depending on

the stress. On the exit side, the stress τ

∗

= 0 corresponds to a certain z

value. Regions of the particle with smaller z are overcome spontaneously. The

diﬀerent stress ranges are clearly visible in Fig. 4.27. The calculations were

4.7 Overcoming of Extended Obstacles 121

performed for the central cut. If the dislocation cuts the particle oﬀ-center,

the cutting face is smaller. Correspondingly, also the activation energy is lower

so that the particles cut at diﬀerent heights produce a whole spectrum of

obstacle strengths.

For particles with a smoothly curved border of the cutting plane exerting a

friction stress τ

, the dislocation can enter the obstacle only if the normalized

maximum force is less than unity, f

=cosφ

min

< 1. In view of Fig. 4.24, this

means that the radius of curvature of the dislocation inside the particle (4.67)

is greater than the radius D/2 of the particle

b(τ

− τ

∗

)

or, with τ

= γ/b and τ

∗

 τ

γD<2E

Thus, while small particles can be cut, the dislocations cannot enter larger

particles. These can be overcome only by bowing out the dislocation in

the matrix to the critical Frank–Read conﬁguration (3.47) shown before in

Fig. 3.20a and c. This process was ﬁrst studied by Orowan [219]. The criti-

cal stress to overcome a regular array of impenetrable obstacles is called the

Orowan stress τ

. In the simple model, the Frank–Read stress is applied

with the inter-particle distance L as the segment length. As the particles can-

not be penetrated, the dislocations have to form loops around them, which is

outlined in Fig. 4.28.

A complex analysis of the Orowan problem in a row of equidistant par-

ticles was given by Bacon et al. [105, 220], including elastic anisotropy as

Orowan loops

Fig. 4.28. Overcoming of a row of impenetrable obstacles of diameter D and inter-

particle distance L by the Orowan process. (a) Dislocation bowing out between

particles in the critical conﬁguration. (b) The dislocation has passed the lower row

of particles and has formed Orowan loops around them

122 4 Dislocation Motion

well as the self-interaction along the dislocation line. The particles of circular

shape on the slip plane of diameter D and interparticle distance L (Fig. 3.20a)

are considered impenetrable obstacles of the same elastic constants as the

matrix so that the dislocation has to bend around the particle border.

For ﬁnding the equilibrium shape of the segments bowing out between the

particles, numerical calculations were performed using the Brown–Indenbom–

Orlov theorem as described in Sect. 3.2.7. The balance between the applied

stress and the self-stress of the dislocation (3.43) was found by an iteration

treatment. The applied stress was increased by small steps until no balance

was reached. The respective stress is the Orowan stress. In the last stable

conﬁguration, the dislocation branches adjoining the particle on both sides

were always nearly parallel. At higher stresses, the conﬁguration collapses,

and forms a closed loop around the particle before the remaining dislocation

moves away.

The calculations yielded the following results.

• The numerical data on the Orowan stress can be summarized by using line

tension arguments. As pointed out at the end of Sect. 3.2.7, the eﬀective

line tension of strongly bowed segments like those in the Orowan conﬁgu-

ration is given by the line energy E(φ) (energy per dislocation length) of

the segments adjacent to the pinning agents having an orientation angle

φ. If the starting dislocation is a screw dislocation, this is the energy of

an edge dislocation, and vice versa, as noticed already in [221]. In the

general case of a mixed dislocation, the adjacent segments are not always

perpendicular to the direction of the starting dislocation as sketched in

Fig. 4.29a. To shift the dislocation forward, the length of these branches

has to be increased. Thus, the Orowan stress can be written as

(φ)



+ B



where E

(φ) is the prelogarithmic factor of the energy of a straight dis-

location of orientation φ,andr

is the inner cut-oﬀ radius as in (3.15).

B is a numerical constant with an average of 0.65. The outer cut-oﬀ or

screening distance X has to be chosen according to the distance to the

dislocation closest to the considered one. Thus, when L is small compared

to D, X ≈ L should be an appropriate value corresponding to the line ten-

sion solution. On the other hand, for small obstacles with L being large

compared to D, the dislocation segments near the obstacles interact most

strongly with the branches on the opposite sides of the obstacles so that

the screening distance should be X ≈ D. The simplest average between D

and L with the described limiting behavior is the harmonic mean. Thus

(φ)



(D + L)

+0.65



. (4.71)

It is shown in [105, 220] that the numerical calculations ﬁt this relation

well.

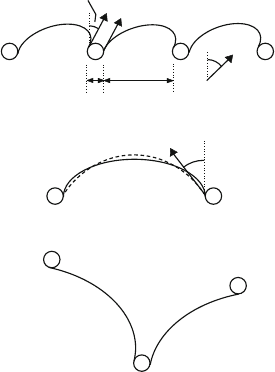
4.7 Overcoming of Extended Obstacles 123

φ)

Fig. 4.29. Orowan process of a mixed dislocation in an anisotropic crystal. (a)Dis-

location bowing out between particles. (b) Schematic of the comparison between the

shape of a bowed segment calculated by the self-stress method (solid line)andthe

respective line tension analogue (dashed line). (c) Triplet of particles for calculating

the breaking condition of the dislocation at the central obstacle B for the simulation

of the Orowan stress in a random array of obstacles after [222]

• Elastic anisotropy may be considered by calculating E

(φ)bymeansof

anisotropic elasticity theory. For a number of metals, the respective line

energy and line tension data are compiled in the form of Fourier coeﬃcients

in [98]. The angle φ depends on the character of the dislocation β and the

crystal system. It is zero for screw and edge dislocations but may amount

up to 30

◦

for β =60

◦

. For details, see [105]. To express the results in terms

of parameters of isotropic elasticity, it is possible to deﬁne a shear modulus

by μ

=4πE

,whereE

is the prelogarithmic term of the energy of

a screw dislocation, and a Poisson ratio ν

by 1 −ν

= E

,withE

being the prelogarithmic term of the energy of an edge dislocation. Both

energies are calculated by anisotropic elasticity theory.

• The inﬂuence of the dislocation self-interaction can be observed by com-

paring the shape of the bowed-out dislocation segments in the critical

conﬁguration determining the Orowan stress calculated by the self-stress

method (solid line in Fig. 4.29b) with that following from the line tension

model (dashed line). The line calculated by the self-stress method touches

the obstacles in perpendicular direction (in the ﬁgure) as described ear-

lier. The dislocation line in the line tension solution, that is, the solution

with L appearing in the logarithmic factor exhibiting approximately the

same swept area, touches the particle at an angle φ. Thus, the eﬀect of

124 4 Dislocation Motion

the self-interaction is to pull both branches attached to the obstacle closer

together. Accordingly, in the line tension approximation, the normalized

force on the obstacle according to (3.48) and (4.49) is smaller than unity.

Consequently, in the line tension model impenetrable obstacles appear as

penetrable ones with a breaking force f

< 1.

To include randomness of the distribution of the particles into the self-

stress calculations of the Orowan stress, computer simulations similar to those

in [192] were performed for small particles with D ≤ 0.1 L in the limit of

isotropic elasticity and ν = 0 [222]. The stability of the dislocation near

an individual obstacle like B in the triplet ABC of Fig. 4.29c is primarily

determined by the interaction between the two bowing segments AB and BC.

Therefore, the breaking conditions of such triplets were calculated over a wide

range of parameters using the self-stress relaxation technique outlined earlier.

These results were represented by an empirical formula to be incorporated into

the computer simulation code of the motion of a dislocation through a random

array of particles. For this simulation, the dislocation segments neighboring

the triplets were represented by two straight lines and all farther segments

by single straight lines. The self-stress of all these straight segments at the

position of the triplet was calculated and added to the applied stress. Thus,

the motion of the dislocation was simulated without relaxation or iteration

treatments. The result can be written again in a line tension analogue with

the eﬀect of the self-interaction expressed by a normalized breaking force f

smaller than unity or a breaking angle φ diﬀerent from zero

2Γ

cos φ



0.8+

2φ

5π



cos φ



, (4.72)

with

Γ = E

μb

4π

1.2 L

for ν =0and

cos φ =

ln(3.3D/r

)

ln(0.8L/r

)

In these formulae, the line tension is that of a freely bowing segment dis-

regarding the self-interaction. The normalized breaking force cos φ considers

the self-interaction, and the bracketed term represents the inﬂuence of the

random distribution of the particles, which reduces the ﬂow stress as in [192].

The topics of this section are important for the understanding of precip-

itation hardening and particle strengthening. Relevant reviews are found in

[223–225]. If a metal is alloyed with some other substance and subjected to

a suﬃciently high temperature, the additions may solve in the matrix. These

solutes can be treated as localized obstacles, giving rise to solution hardening.

Depending on the obstacle strength, extension, and concentration, Friedel or

Mott statistics has to be applied. This state can be frozen in by rapid quench-

ing to a low temperature. Controlled by the phase diagram and the ability

4.7 Overcoming of Extended Obstacles 125

Fig. 4.30. Precipitation hardening in the technical alloy Al-4.54Zn-1.18Mg (wt%)

homogenized for 2 h at 400

◦

C, quenched and aged for 7 days at room temperature.

The precipitates of the η



phase are visible as dark dots. Micrograph from [226]

of diﬀusion, that is, by annealing at a suﬃciently high temperature, a sec-

ond phase may precipitate. In any case, the ﬂow stress is proportional to the

reciprocal value of either the square lattice distance l

or the inter-particle

distance L. Thus, the ﬂow stress is approximately proportional to the square

root of the concentration of the obstacles on the slip plane. If the precipitates

are small, they are often coherent and may be treated as elastic inclusions as

outlined in Sect. 3.2.6. During further annealing, the defect structure coarsens,

with larger particles growing at the expense of smaller ones. This process is

called ageing. For penetrable particles with a friction stress τ

, the obstacle

strength increases with increasing particle size. This leads to an increasing ﬂow

stress or age hardening. Above a critical size, the dislocations cannot enter

the particles any longer. They bow out around the particles and overcome

them by forming Orowan loops. At this stage, the obstacle strength no longer

increases and the decrease of the obstacle concentration leads to a decrease of

the ﬂow stress. The alloy with the maximum ﬂow stress is in the peak aged

state. Afterwards, it is overaged. A typical example of these precipitation

hardened alloys are the aluminium alloys discussed in Sect. 8.1. Figure 4.30

shows dislocations during in situ deformation in an HVEM of an Al-Mg-Zn

alloy hardened by precipitates of the η



phase. The particles are visible as

small dark dots. Because of their high obstacle strength, the dislocations are

strongly bowed-out. Usually, incoherent particles cannot be intersected. Such

particles are, for example, oxide dispersoids in metal matrices, forming the

so-called oxide dispersion strengthened (ODS) alloys described in Sect. 8.3.

At low temperatures, the oxide particles are overcome by the Orowan mecha-

nism. They are very stable also at high temperatures being then surmounted

by climb.

126 4 Dislocation Motion

As long as the activation energy to overcome the obstacles and the num-

ber of involved atoms are small, the particles are passed by the aid of thermal

activation, and the ﬂow stress depends on the temperature and the deforma-

tion rate. The dislocation motion is then jerky on the scale of the particle

distance. This is a small scale for solution hardening with Mott statistics, and

a larger one for precipitation hardening with Friedel statistics. The force–

distance curve of even relatively large particles may have a narrow tip so that

thermal activation may still play some role. The Orowan mechanism for large

impenetrable particles is of fully athermal character as the energies to form

even small dislocation loops are too high for thermal activation, as mentioned

in Sect. 3.2.2. In this case, the stress has to be high enough to overcome the

strongest conﬁgurations. The dislocation motion is then very jerky on a large

scale.

4.8 Dislocation Intersections

In most cases of plastic deformation, dislocation motion is not restricted to

a single slip system, instead several slip systems are activated simultaneously

(multiple slip). Then, the moving dislocations have to intersect dislocations

of other slip systems, usually having diﬀerent Burgers vectors. These dis-

locations are called forest dislocations. The process of dislocation cutting is

very complex. The crossing dislocations experience a mutual long-range elastic

interaction, as outlined in Sect. 3.2.5. In general, the interaction includes com-

ponents of the interaction force out of the glide plane, which may induce cross

glide or climb. Within the glide plane, the interaction leads to pinning either

by attractive or repulsive forces with the dislocations bowing out between

the forest dislocations. Figure 4.31 presents an example of an edge disloca-

tion pinned by a screw dislocation with perpendicular Burgers vector (arrow).

The bow-outs may be strong so that the moving dislocations have to form the

critical half-circle (Frank–Read) conﬁguration (3.47) to overcome the forest

dislocations. Then, the segment length L equals the average distance between

the forest dislocations 

−1/2

,if

is the forest dislocation density. Thus, the

contribution of the dislocation forest to the ﬂow stress can be written as

forest

= α

μb

2π

√



. (4.73)

The factor α

describes the strength of the actual interaction force and

should be less than 2π. An alternative process is the formation of dislocation

junctions if the interaction is attractive and reduces the dislocation energies

(see Sect. 3.2.2 and Fig. 3.10). For b.c.c. crystals, values of α

≈ 0.4 π were

computed by virtual displacement of the triple nodes bounding the junctions

[227]. In addition to these long-range interactions, there is a short-range con-

tribution due to the formation of jogs or kinks in both dislocations as already

shown in Fig. 3.16. As described in Sect. 3.2.5, the formation energy of the jogs

4.8 Dislocation Intersections 127

0.5 µm

Fig. 4.31. Edge dislocation that is strongly pinned by a screw dislocation of per-

pendicular Burgers vector during in situ deformation of an MgO single crystal at

room temperature. From the work in [164]

is approximately equal to the core energy E

= μb

/10 which, being in the

order of magnitude of 0.5 eV, is well within the range of thermal activation at

room temperature. If the dislocations are dissociated, the jog energy involves

also the energy for the constriction (see Sect. 4.3). In ionic crystals, where the

inserted half-plane consists of more than one lattice plane, jogs of diﬀerent

heights are possible. Then, jogs of small height (e.g., half-jogs in the NaCl

structure) are electrically charged.

As the discussion has shown, the interaction between the dislocations

during the intersection has both long-range and short-range components.

Therefore, it is diﬃcult to determine the interaction proﬁle and the total acti-

vation energy. The activation distance is certainly less than about 10b,andthe

segment length equals the distance between the forest dislocations ≈ 

−1/2

.As

the forest density for multiple slip increases with increasing plastic strain, the

contribution of dislocation intersections to both the ﬂow stress and the acti-

vation parameters depends on the strain. Unfortunately, also other processes

depend on the strain so that it is diﬃcult to clearly verify the contribution of

dislocation cutting.

The inﬂuence of the forest dislocation density on the ﬂow stress can quite

directly be studied by so-called latent hardening experiments as mentioned

in Sect. 4.3. Figure 4.32 shows a plot according to (4.73) of the secondary

ﬂow stress in NaCl single crystals as a function of the square root of the for-

est screw dislocation density generated during a primary deformation up to

diﬀerent plastic strains [228]. Linear regression analysis yields a straight line

with α

≈ 1.4π, where the anisotropic shear modulus μ =



− c

) /2

was taken. Considering that in addition to the screw dislocations counted in

Fig. 4.32 also edge dislocations contribute to the forest, it follows that α

≈ π,

which meets the theoretical expectation. The small intercept on the τ

axis

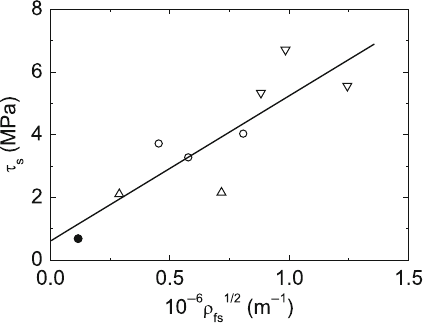
128 4 Dislocation Motion

Fig. 4.32. Latent hardening experiments on high-purity NaCl single crystals

deformed along two diﬀerent 100 axes. Dependence of the secondary ﬂow stress

on the square root of the density of screw dislocations produced during a primary

deformation on a slip system that is stress-free during the secondary deformation.

0% primary plastic shear strain (full circle), 3% (upward triangle), 6% (open circles),

12% (downward triangles). Data from [228]

indicates a ﬂow stress contribution from the interaction between dislocations

and aliovalent impurities. According to measurements of the strain rate

sensitivity, the contribution of forest cutting is essentially of athermal nature.

After their formation, the jogs have to move together with the dislocation.

As a jog is a piece of dislocation line that is not contained in the slip plane,

it has its own slip plane deﬁned by its Burgers vector and line vector as

mentioned above in Sect. 3.1.2 and sketched in Fig. 3.5. According to the latter,

jogs can glide (i.e., move conservatively without the production or annihilation

of point defects) in the direction of the Burgers vector of the dislocation.

This is the forward direction in edge components of dislocation loops but the

direction along the dislocation in the screw parts. In mixed dislocations, jogs

glide in a direction inclined to that of the dislocation line. As the jogs do not

glide on the main glide plane of the dislocation, which is usually a plane of

low glide resistance, they may experience additional glide resistance so that

the dislocation has to form a cusp at them. This is shown in Fig. 4.33. The

dislocation moving on the slip system with Burgers vector b

mainly has an

edge orientation. It has cut dislocations with the projection of the Burgers

vector b

of the slip system with a horizontal trace and obtained several

jogs, which cause cusps in the dislocation line (arrow). As the curvature of

the dislocation between the cusps indicates, the jogs cause a considerable

resistance to the motion of the dislocation. This resistance should be higher in

dislocations with large screw components as there the jogs have to move faster

4.9 Dislocation Motion at High Velocities and Low Temperatures 129

Fig. 4.33. Intersection between oblique slip bands during in situ deformation of an

MgO single crystal with conservative motion of jogs in an edge dislocation (arrow).

From the work in [79]

than the rest of the dislocations. Jogs in pure screw dislocations can move

with the dislocations only by climb, that is, by the production or absorption

of point defects. This process is called jog dragging and will be described in

Sect. 4.10.5.

4.9 Dislocation Motion at High Velocities

and Low Temperatures

The main topic of this book is dislocation dynamics under normal conditions,

that is, at dislocation velocities up to the centimeter-per-second range and

at temperatures between about liquid nitrogen temperature and about 90%

of the melting temperature. At high velocities and low temperatures, special

eﬀects have to be considered, which will only brieﬂy be outlined here, mainly

following Hirth and Lothe [12]. See also the review by Alshits and Indenbom

[229].

The elastic properties of dislocations described in Sect. 3.2 are those of

resting dislocations. These solutions are valid up to velocities of some frac-

tions of the velocity of sound. To treat dislocation motion at high speeds,

inertial terms have to be included into the elastic equilibrium condition as

body forces −ρ



∂

/∂t



caused by the acceleration of the volume ele-

ment. Here, ρ

is the mass density of the material and t the time. For a

screw dislocation in an elastically isotropic medium, the diﬀerential equation

deﬁning the stress ﬁeld of the dislocation takes the form of the static one if