Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

222 7 Ceramic Single Crystals

be studied. They can easily be cleaved, in some cases yielding almost atomi-

cally smooth surfaces (e.g., {100} faces on NaCl crystals), which facilitates the

specimen preparation and enables the surface decoration of monatomic slip

steps (Figs. 4.9 and 4.12). Besides, chemical etching is well suited to image the

points where dislocations emerge through the surfaces. From combinations of

measurements of diﬀusion, electrical conductivity, and dielectric and mechan-

ical relaxation, the spectrum of point defects is comparatively well known,

that is, from the intrinsic defects like vacancies in both sub-lattices (and in

some materials interstitials) to associates of aliovalent impurities or additions

with vacancies and their agglomerates. Thus, several interactions between dis-

locations and point obstacles can well be investigated. The famous studies of

Johnston and Gilman [19, 276] on the dislocation mobility and kinetics in

LiF single crystals certainly beneﬁted from these advantages. A drawback is

the strong sensitivity to radiation damage, so that TEM observations require

cryo-microscopy.

7.1.1 Crystal Structure and Slip Geometry

Several alkali halides and oxides crystallize in the sodium chloride structure.

As shown in Fig. 7.1, it consists of two f.c.c. lattices of the two ions shifted

by a/2 with respect to each other. The Burgers vector is a/2110.Thus,the

extra half-plane of an edge dislocation consists of two inserted half-planes

to preserve electrical neutrality of the crystal. Full jogs in the dislocation line

have the height of b. They are electrically neutral. Half-jogs carry an electrical

charge of ±e/2. Correspondingly, dislocations with unequal numbers of half-

jogs of diﬀerent sign are electrically charged. The dominating slip planes are

of type {110} so that there exist six independent slip systems. Always pairs

of two systems are perpendicular to each other. For one primary slip plane,

another one is perpendicular and the four others are oblique. Accordingly,

the secondary slip systems are called orthogonal or oblique slip systems. At

a 100 deformation axis, two slip systems have zero orientation factors and

four have m

=0.5, while along 111 all {110}1

10 slip systems have zero

orientation factors. Then, also {001}110 systems are activated.

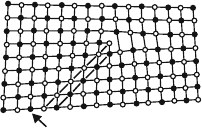
Fig. 7.1. Sodium chloride structure with an edge dislocation. The two ion species

are marked by open and full circles

7.1 Alkali Halides 223

7.1.2 Dislocation Dynamics

In the following, the dislocation dynamics and plastic deformation of sodium

chloride single crystals will be described, as a typical example also of other

alkali halides. Dislocation velocities were measured as a function of the applied

stress by Gutmanas et al. [389, 390] using the stress pulse-double etching

technique (Sect. 2.2). In a double-logarithmic plot of v

vs. τ, the curves look

very similar to those of LiF in Fig. 4.41. At low velocities between about 10

−9

and 1 m s

−1

, the plots follow straight lines indicating power law dependencies

(4.103) with high values of the stress exponents m. Above about 10 m s

−1

the curves bend down, which corresponds to lower stress exponents. Again,

edge dislocations have a slightly higher mobility than screws. Characteristic

for alkali halide crystals is a strong reduction of the dislocation mobility by

the addition of aliovalent cationic impurities. The addition of the divalent

impurities Sr

and Ca

to NaCl has been well studied. In the low-velocity

region, the stress exponents range between 30 and 10, and in the high-velocity

one they range between 2.6 and 1 for crystals with 10

−2

mole% Sr

and

for nominally pure NaCl, respectively. As in most materials, the dislocation

velocity in the high-velocity range is controlled by viscous damping. It will

be shown below that at low and intermediate velocities and at temperatures

not too low, the dislocation mobility is governed by the interaction between

dislocations and defects containing the divalent impurities.

7.1.3 Macroscopic Deformation Properties

Ionic crystals and sodium chloride, in particular, demonstrate well in which

way the diﬀerent processes control the plastic deformation in the various tem-

perature ranges. A summary was given by Haasen [391]. Several data on the

deformation of NaCl single crystals have been discussed in Part I, Sects. 4.8,

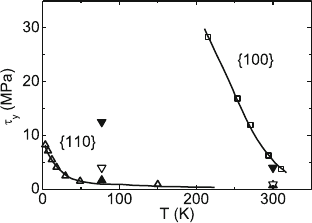
5.2.1, and 5.2.2. Figure 7.2 presents the temperature dependence of the yield

stress up to about room temperature for the {110} and { 100} slip planes.

The ﬁgure indicates a strong low-temperature increase of the yield stress, for

the {110} slip plane below about 50 K and for the {100} plane already below

room temperature. In addition, the yield stress is remarkably enhanced by the

addition of divalent cationic impurities. As described earlier, the impurities

directly inﬂuence the dislocation mobility.

The low-temperature increase of the yield stress and its diﬀerence between

the slip planes are ascribed to the action of the Peierls mechanism. In ionic

crystals, the elastic theory of the Peierls model as described in Sect. 4.2 fails,

particularly in explaining the diﬀerences between the various ionic crystals.

The experimental Peierls stresses reduced by the square of the ion valency

have an inverse dependence on the sum of the polarizabilities of the matrix

ions [393]. Realistic values of the Peierls stress for the {110} slip planes were

calculated by Granzer et al. [132] using an atomistic model. They obtained

224 7 Ceramic Single Crystals

Fig. 7.2. Dependence of the shear yield stress of NaCl single crystals on the tem-

perature. Data from [392] for nominally pure crystals, {110} slip plane (small open

upward triangles), {100} slip plane (open squares). Data from [177] already shown

in Fig. 5.26 for the {110} slip plane, 1.7 ppm residual impurities (large full upward

triangles), 32 ppm Ca

(large open downward triangles), 136 ppm Ca

(large full

downward triangles)

values between 14 and 22 MPa in the correct order of magnitude of the low-

temperature increase of the yield stress in Fig. 7.2. For the {100} plane, the

summation over the ion rows is diﬃcult. According to Gilman [394], the high

lattice friction stress on this plane results from the close neighborhood of

always two ions of equal charge after a shift of the dislocations by b/2.

The strong dependence of the dislocation mobility and the yield stress on

the concentration of divalent cation impurities at intermediate temperatures

is due to the elastic interaction between the moving dislocations and elastic

dipoles with tetragonal stress ﬁelds formed by associates of the impurities and

their charge-compensating cation vacancies. The degree of association is con-

trolled by the interaction energy between the impurities and vacancies through

the law of mass action. In the respective temperature interval, practically all

impurities are associated with vacancies. At high impurity concentrations, the

associates may agglomerate to higher complexes. At lower temperatures, the

associates act as ﬁxed localized obstacles to the dislocations. The interaction is

of Fleischer type (Sect. 3.2.6). At higher temperatures, the dipoles may reori-

ent in the stress ﬁeld of the dislocations by diﬀusion jumps of the vacancies

around the impurities leading to a Snoek eﬀect interaction (Sect. 4.11). These

theoretical concepts were applied to alkali halide crystals by Frank [395].

In the range of operation of these mechanisms, the macroscopic deforma-

tion of NaCl crystals containing Ca

impurities has extensively been studied

by Appel [396–398]. Nominally pure and doped crystals were cooled by a

thermoelectric cooler, which allowed quick changes of the temperature. The

activation volume V and (Gibbs free) energy ΔG were determined by strain

rate and temperature cycling tests as outlined in Sect. 4.1. In addition, the

eﬀective stress τ

∗

was measured by long-time stress relaxation tests, supple-

mented by etch pit countings of the dislocation density . As the total (shear)

ﬂow stress τ as well as the eﬀective stress τ

∗

depend on the plastic strain, the

7.1 Alkali Halides 225

ﬂow stress was assumed to consist of the following parts

τ = τ

+ τ

∗

with

∗

= τ

∗

+ τ

∗

, (7.1)

where τ

∗

is the chemical hardening due to aliovalent cationic impurities and

∗

is a work-hardening contribution to τ

∗

. While τ

∗

is assumed to depend

only on the state of the impurities and the thermodynamic variables, τ

and

∗

in addition depend on the strain and on τ

∗

. In Sect. 4.5.1, the superposition

rules of two types of thermal obstacles were discussed. For obstacles of not

very diﬀerent strengths and concentrations, a quadratic superposition law

holds (4.59), while for many weak and few strong obstacles, the stress parts

superimpose linearly (4.63). It will be shown that the strain-depending part of

the eﬀective stress consists in the intersection of dislocations created during

the deformation. This interaction is much stronger than the Fleischer-type

interaction with elastic dipoles so that the linear rule (7.1) can be applied.

The diﬀerent stress parts were varied by changing the temperature T ,the

strain rate ˙ε,thestrainε, and the divalent impurity concentration c

.The

variation in the thermodynamic variables T and ˙ε should be equivalent. At low

plastic strains, yield drop eﬀects do not occur after changing the deformation

conditions below 250 K, indicating that the microstructure remains constant

during the stress changes.

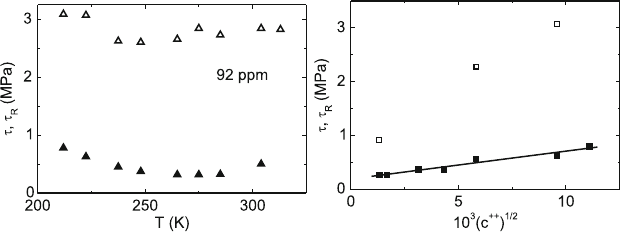
Figure 7.3a presents the dependence of the ﬂow stress τ and the stress

relaxing during long-time stress relaxation tests on the temperature for a

ﬁxed concentration c

= 92 ppm of divalent cationic impurities. τ

is sup-

posed to be equal to τ

∗

. The ﬁgure shows that the athermal stress component

= τ − τ

∗

is the main part of the total ﬂow stress, amounting to more

than 70%. However, this stress part is not constant but depends, for exam-

ple, on the concentration c

of divalent additions, as outlined in Fig. 7.3b. It

(a)

(b)

Fig. 7.3. Dependence of the ﬂow stress τ (open symbols) and the relaxation stress

(full symbols) on the temperature at a concentration of Ca

of 92 ppm (a),

and on the square root of the Ca

concentration at a ﬁxed temperature of 223 K

(b). Strain rate 4.2 × 10

−4

−1

. Data from [396]

226 7 Ceramic Single Crystals

was discussed in Sects. 5.2.1 and 5.2.2 that the athermal stress originates from

long-range interactions between dislocations. The corresponding linear depen-

dence of the ﬂow stress on the square root of the dislocation density (5.11) was

ﬁrst proved in pure NaCl crystals, where τ

∗

is small, in [399]. Later on, the

diﬀerent inﬂuences of the densities of primary and secondary dislocations were

demonstrated by cryo-TEM in [400]. The total dislocation density follows the

Taylor law (5.11) with the numerical constant α =0.7π. For the present mate-

rials, the square root dependence was shown above in Fig. 5.15. As discussed

there, this relation is not universal, and τ

depends on τ

∗

and correspondingly

also on the temperature and the strain rate. The eﬀective stress follows quite

well a square root dependence on the Ca

concentration (Fig. 7.3b).

In Fig. 7.3a, both τ and τ

∗

exhibit two temperature ranges. First, they

decrease with increasing temperature in the normal way, and above 250 K

they remain constant or even increase. These are the ranges of the short-range

Fleischer type interaction with the Ca

vacancy dipoles at low temperatures,

and the Snoek eﬀect interaction at higher ones.

At ﬁrst, the contribution τ

∗

of the Fleischer type interaction to the eﬀective

stress will be discussed. It is assumed that τ

∗

is small at low plastic strains

so that the stress dependence of the activation parameters can be interpreted

by using the Fleischer approximation (3.35). Neglecting Friedel statistics, for

the dependence of the activation volume on the eﬀective stress follows

V =Δdlb = b





∗



1/2

− 1



and for the Gibbs free energy

ΔG =ΔG

◦



1 −



∗



1/2



Here, τ

= F

/(lb) is the stress for athermally surmounting the obstacle array,

and ΔG

is the activation energy at zero stress. The latter equation is identical

with (4.60). The plot of V vs. τ

∗−1/2

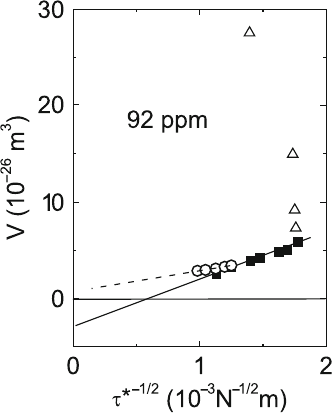
is presented in Fig. 7.4 for crystals with a

concentration of 92 ppm. τ

∗

is varied by the temperature, the strain rate,

and the plastic strain. Data resulting from changes in the temperature and the

strain rate form a single curve, as expected for a single thermally activated

mechanism. Below 250 K, it is a straight line (full squares) with the slope

1/2

and the intercept lb

. Similar plots were obtained also for the other

concentrations. The values of the obstacle distance l from the intercept

are compared with those from the concentration c

, l

= a/



(4/3)c

,in

analogy with (4.48). a is the lattice constant. The numerical factor considers

the geometry of dislocations passing elastic dipoles of diﬀerent orientations

on nearest planes. It turns out that l ≈ l

for low c

,andl>l

for

higher ones. The disagreement for higher concentrations does not indicate

the beginning of agglomeration of the individual elastic dipoles but results

7.1 Alkali Halides 227

Fig. 7.4. Dependence of the activation volume on the reciprocal square root of the

eﬀective stress in NaCl single crystals of 92 ppm Ca

. Eﬀective stress varied by

applying diﬀerent temperatures and strain rates at a constant low plastic strain,

temperatures between 212 and 248 K (full squares and solid extrapolation line)and

between 265 and 304 K (open triangles). Eﬀective stress varied by increasing plastic

strain at 223 K and 4.2 × 10

−4

−1

(open circles and dashed extrapolation line). Data

from [396]

from changes in the pre-exponential factor in the Arrhenius equation, which

are reﬂected in changes in the Gibbs free energy of activation [302]. Besides,

agglomeration contradicts the linear plot of τ

∗

vs. c

++1/2

in Fig. 7.3b. Slope

and intercept together of the plot in Fig. 7.4 yield ΔG

. The consistency of the

results was checked by plots of V vs. T following from the Fleischer potential,

and by comparing the activation energies calculated from V vs. τ

∗−1/2

by the

formalism above, with the values from temperature and strain rate cycling

tests and applying (4.13) and (4.15). The agreement is satisfactory. The Gibbs

free energies of activation for small strains increase from 0.22 to 0.34 eV with

an increasing concentration of Ca

[302].

At temperatures above 250

◦

C, the activation volumes (open triangles in

Fig. 7.4) strongly deviate from those of the low-temperature Fleischer type

range. They show an inverse dependence on the eﬀective stress, that is, a

decreasing strain rate sensitivity with increasing stress, which contradicts the

usual thermally activated mechanisms. The inverse dependence points at dif-

fusion processes involved in the dislocation motion and will be discussed in

more detail in connection with the occurrence of yield stress anomalies in

intermetallic alloys in Chap. 9. The eﬀect is connected with strain ageing and

is ascribed to the induced Snoek eﬀect (Sect. 4.11) [395,398]. After stress relax-

ation tests (stopping the deformation machine) for diﬀerent durations, sharp

228 7 Ceramic Single Crystals

Fig. 7.5. Section of a stress–strain curve showing yield point eﬀects due to strain

ageing of a crystal with 136 ppm Ca

at 266 K and a strain rate of 10

−4

−1

.Data

from [398]

yield points arise during reloading the samples as illustrated in Fig. 7.5. The

stress increments of the yield points depend on the concentration c

,the

temperature, and the ageing time [398]. Arrhenius plots of the time constant

of the saturation process and the times to saturation yield an activation energy

of about 0.55 eV. This is slightly lower than the energy of 0.65–0.7eV for reori-

entation of the elastic dipoles, measured by dielectric relaxation. It disagrees

with the Cottrell eﬀect, which requires diﬀusion of the cation impurities and

which has a much higher activation energy.

Figure 7.4 contains also some data points resulting from a variation of

the eﬀective stress by an increasing plastic strain under otherwise constant

conditions (open circles and dashed extrapolation line) [397]. These data

points suggest a strain-induced contribution to the thermal part of the ﬂow

stress, which is connected with an increase in the strain rate sensitivity.

The data points deviate from the straight line belonging to the interaction

with tetragonal defects discussed earlier. It was proved that the Gibbs free

energy of activation is independent of the plastic strain. According to (4.8),

the Gibbs free energy determines the pre-exponential factor of the Arrhenius

equation. Thus, the strain dependence does not result from a change in the

pre-exponential factor for overcoming the tetragonal defects. New short-range

obstacles should be created as the concentration and state of agglomeration

of the tetragonal defects is not expected to change during plastic deformation.

As pointed out in [206,401], a separation of the thermal stress parts is pos-

sible if these can be varied independently. This is possible ﬁrst by measuring

the activation parameters of crystals with diﬀerent concentrations of Ca

the same small strain, and second, by studying the strain dependence on each

individual crystal. Applying the Arrhenius equation (4.8) and (4.3), as well

as the linear superposition rule (7.1), there follows

∗



ΔF

+ kT ln

˙ε





ΔF

+ kT ln

˙ε



. (7.2)

For ˙ε and T being constant, the factors ΔF + kT ln( ˙ε/ ˙ε

)andtheactiva-

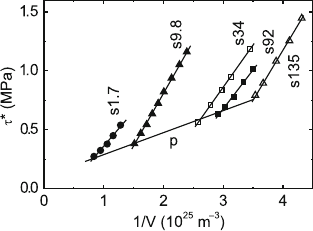
tion distances Δd are constant. Figure 7.6 is the respective plot of τ

∗

vs.

7.1 Alkali Halides 229

Fig. 7.6. Dependence of the eﬀective stress on the reciprocal activation volume

in NaCl single crystals at 223 K. The eﬀective stress is independently varied by

using crystals of diﬀerent concentrations of Ca

(extrapolation line p)andby

applying diﬀerent plastic strains (extrapolation lines s with indication of the Ca

concentrations in ppm). Data from [397]

the reciprocal activation volume 1/V with the extrapolation lines p of mea-

surements at small strains with diﬀerent Ca

concentrations, and s for the

variation of τ

∗

by work-hardening. The slope of curve p yields the ﬁrst term

in parentheses in (7.2), that is, the work term V

∗

=ΔF

+ kT ln( ˙ε/ ˙ε

whereas the slopes of the curves s equal the second term in parentheses V

∗

From the intercepts, the ratios τ

∗

/τ

∗

and V

can be calculated. The result

is that for small strains, the impurity part dominates the eﬀective stress (as

assumed above) except for small impurity concentrations. The Helmholtz

free energy of activation of the strain-dependent process is obtained from

the strain-independent Gibbs free energy quoted above and the work term,

ΔF

=ΔG + V

∗

≈ 0.6 ...0.8eV.

The parameters determined ﬁt the intersection of forest dislocations as

the strain-induced hardening process. In agreement with this suggestion, the

square root of the dislocation density during hardening shows a linear depen-

dence on the reciprocal activation volume, leading to an activation distance

of Δd

≈ 0.6 ...0.7 b. This distance and the activation energy correspond well

with the process of jog formation, the activation energy of which approxi-

mately equals the core energy μb

/10 (3.16). This energy characterizes only

the thermal part of the interaction between the cutting dislocations. A great

part of this interaction is of long-range character, in agreement with the

large athermal ﬂow stress component τ

. This is supported by the observa-

tion that the latent hardening by forest dislocations discussed in Sect. 4.8 is

of athermal nature.

7.1.4 Summary

In the literature, plastic deformation of ionic crystals is frequently being dis-

cussed from two diﬀerent points of view. One is considering the mechanisms

controlling the dislocation mobility, that is, the thermal part of the ﬂow stress,

230 7 Ceramic Single Crystals

while the other one is regarding the relation between the ﬂow stress and the

dislocation density, that is, the athermal stress part. The discussion above has

shown that both aspects have to be considered simultaneously. Except at very

low temperatures, the athermal stress τ

dominates the ﬂow stress. However,

it is not a constant as supposed in many papers but depends on the eﬀective

stress τ

∗

, and correspondingly on the chemical hardening state and on the

deformation parameters.

The dislocation mobility and thus the thermal part of the ﬂow stress are

controlled by the Peierls mechanism at very low temperatures and by the

tetragonal defects (elastic dipoles) formed by aliovalent cationic impurities

or additions and their charge-compensating vacancies. Up to about 250 K,

these complexes have a short-range Fleischer type interaction with the glid-

ing dislocations with activation energies between 0.25 and 0.45 eV. Above this

temperature, the vacancies may rotate around the impurities in the stress ﬁeld

of the dislocations resulting in the induced Snoek eﬀect. It is interesting to

compare the stress exponents m determined from the dislocation mobility by

means of the selective etching method and from the macroscopic deforma-

tion data. From the latter, m can be calculated by m = σ

∗

/r = τ

∗

/(m

(4.11). Usually, τ

∗

is not available so that the experimental stress exponent



= σ/r = τ/(m

r) (4.12) is used. Table 7.1 compares the discussed m

values. For the pure crystals, the data of m agree very well, irrespective

of the temperature. For the doped crystals, the agreement holds only for

room temperature, which is in the range of the Snoek eﬀect interaction. The

high m value results from the low strain rate sensitivity characteristic of

the diﬀusion-controlled dislocation mobility. The low-temperature value from

the macroscopic experiments is much lower, corresponding to the Fleischer

type range. The experimental m



values calculated from the total stress τ are

mostly too high. They do not represent the processes governing the dislocation

mobility. One should therefore take care in interpreting m



data in connection

with the dislocation mobility.

The change of the activation parameters with increasing plastic strain can

be attributed to an increasing frequency of dislocation intersections. While

Table 7.1. Stress exponent m from selective etching [390] and from macroscopic

deformation tests [396] calculated from the strain rate sensitivity r and the eﬀective

stress τ

∗

and m



from the total stress τ (see text)

(ppm) T (K) Etching m from τ

∗



from τ

Pure RT 10

248 8 40

223 10 35

92 (Ca

) RT 33 187

223 7 36

100 (Sr

)RT 30

7.2 Magnesium Oxide 231

the main part of the energy necessary for dislocation cutting originates from

the long-range dislocation interaction, which contributes to the athermal part

of the hardening, the top of the interaction potential is overcome by the aid

of thermal activation. The activation energy is in the order of magnitude of

0.7 eV. Thus, the assumption made for applying the linear superposition rule

between the two thermal ﬂow stress parts is justiﬁed. The obstacle spectrum

consists of many weak obstacles and few strong ones.

7.2 Magnesium Oxide

Oxide crystals cover materials with very diﬀerent dislocation behavior and

macroscopic deformation properties. Two examples are presented here, mag-

nesium oxide (MgO), which is plastic down to helium temperatures, and

zirconia–yttria (ZrO

–Y

) alloys, which are brittle up to about 800

◦

under normal deformation conditions. MgO has the same crystal structure

and slip geometry as NaCl. Thus, for the specimens with 100 loading axes,

the orientation factor is m

=0.5.

7.2.1 Microscopic Observations

After some early studies of the plastic deformation of MgO single crystals

(e.g., [402–404]), joint work was carried out in the Institute of Solid State

Physics (Acad. Sci. of U.S.S.R.), Chernogolovka, and the former Institute

of Solid State Physics and Electron Microscopy (Acad. Sci. of G.D.R.), Halle

(Saale), covering TEM and in situ straining experiments, measurements of the

dislocation velocity, and macroscopic deformation experiments. All specimens

were obtained from the same large single crystal block. It contained about

300 ppm aliovalent impurities, mainly Fe

. In as-grown and annealed crys-

tals, these impurities form small precipitates. The dominating microstructural

observation is the interaction of the moving dislocations, with these precip-

itates acting as localized obstacles. Examples and micrographs from the in

situ straining experiments were presented in several sections of Part I, for

example, in Fig. 4.13. Figures like this and the video recordings discussed

below allowed detailed analyses of the statistical and kinematic properties of

the dislocation motion in the ﬁeld of localized obstacles. A problem in inter-

preting the results of the in situ experiments was the occurrence of radiation

hardening during electron irradiation of the specimens inside the HVEM [334].

The irradiation increases the ﬂow stress of the in situ specimens by about 30%

without qualitatively aﬀecting the dislocation motion in the observed speci-

men area. It is therefore assumed that the hardening does not seriously aﬀect

the semi-quantitative conclusions drawn from these experiments.

In all experiments described below, the specimens had a [001] foil normal

and a [010] tension or compression direction. Orthogonal slip bands extending

in [100] direction have 1/2011 Burgers vectors inclined with respect to the