Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

200 5 Dislocation Kinetics, Work-Hardening, and Recovery

from the diﬀusing solutes, for example, by forest dislocations [350] or precipi-

tates. After the dislocation has overcome the pinned and aged conﬁguration,

the activation energy takes the lower value of ΔG =ΔF − Vτ

∗

so that the

dislocation may move a greater distance until it is pinned again. The plastic

strain rate is then given by

˙ε = ν

Ω exp



−

ΔG



= ν

Ω exp



−

ΔF − Vτ

∗

+Δg (1 − exp [−(ηt

)

])



. (5.24)

is a vibrational frequency, and Ω an elementary strain, that is, the strain

occurring if all dislocations overcome an obstacle. Here, the waiting time for

ageing is set equal to the average waiting time for thermal activation, t

Ω/ ˙ε. Equation (5.24) can be solved for ˙ε, if the stress dependencies of ΔF and

V are known. A resulting schematical plot of τ

∗

vs. ln ˙ε or ln ˙γ was presented

in Fig. 4.39 illustrating the three ranges discussed already. In range A at low

strain rates, τ

∗

increases owing to an increasing eﬃciency of ageing. In range

B, the dislocations move too fast for eﬀective ageing so that τ

∗

decreases.

Finally, τ

∗

increases again in range C due to the increasing resistance of the

obstacles, which temporarily pin the dislocations. The slope of the curve equals

the strain rate sensitivity r, which is positive in range A, negative in range B,

and positive again in range C as discussed in Sect. 4.11. Plastic deformation

cannot be stable in range B. Thus, if the macroscopic strain rate corresponds

to range B, the specimen may deform at a lower rate in range A, leading to

an increase in τ

∗

. When it reaches its maximum value at the transition to

range B, the deformation can continue under the same stress at a high rate

in range C. This leads to a decrease in τ

∗

until the transition to range B

is reached where the deformation switches back to range A as indicated by

the thick broken arrows in Fig. 4.39. The cycle described corresponds to both

an increase and a drop in stress during serrated yielding. The ﬁgure predicts

also the dependence of the strain rate sensitivity r on the strain rate or the

stress in the stable ranges. In the normal range C of thermally activated

overcoming of obstacles, the curve is bent upwards, which corresponds to

an increase in r or a decrease of the activation volume V = lbΔd with the

stress increasing owing to a decrease of the activation distance Δd. In Friedel

statistics (Sect. 4.5.1), also the obstacle distance l decreases with increasing

stress. In the diﬀusion-controlled range A, however, the curve in Fig. 4.39 must

bend downwards to form the maximum at the transition to range B, that is, r

decreases with increasing stress. The dependence of r on the stress is reﬂected

in the shapes of stress relaxation curves as it will be discussed, for example,

in connection with the ﬂow stress anomaly in intermetallics (Sect. 9). Besides,

the time dependence of the activation energy as expressed in (5.23) leads to

transient eﬀects under nonconstant deformation conditions.

As described so far, all dislocations may move at the same velocity. The

theory reviewed by Zaiser and H¨ahner [351] includes two important extensions.

5.3 Plastic Instabilities 201

• The assumption of equal waiting times t

for all dislocations is replaced

by a distribution function of the waiting times.

• Dislocations moving on parallel slip planes are considered coupled by long-

range elastic interactions. This leads to a synchronization of the waiting

times, that is, to a collective mode of dislocation motion.

Plastic instabilities require both the occurrence of dynamic strain ageing and

the coupling of dislocations. Thus, the Portevin–LeChatelier eﬀect consists

in a localization of slip in time and space. The most important result of the

extended theory is that the strain rate sensitivity r need not be negative as

in the earlier theories. It is suﬃcient if r is close to zero. The low strain rate

sensitivity is necessary for the synchronization of the waiting times.

In the extension of the earlier Kubin–Estrin model in [352], equations sim-

ilar to those described above are coupled with equations describing separately

the evolution of the densities of mobile and forest dislocations. While disloca-

tion pinning and strain ageing take place on a fast time scale, the evolution of

the dislocation structure occurs on a slow time scale. The model reproduces

the negative strain rate sensitivity of the threshold stress for the instability.

While many materials under most conditions deform in a stable way, ser-

rated ﬂow may occur under certain conditions of temperature and strain rate.

The unstable ﬂow results from a combination of diﬀusion-controlled ageing

and pinning and thermally activated surmounting of stronger obstacles. In

this respect, the literature mainly considers the cutting of forest disloca-

tions. However, jerky ﬂow may occur also in single slip so that other obstacles

like precipitates may act as pinning centers. Characteristic of dynamic strain

ageing is the low strain rate sensitivity. Plastic instabilities are a collective dis-

location process where many dislocations act simultaneously. This requires a

coupling in time and space. Accordingly, slip is mostly concentrated in narrow

slip bands. A prerequisite to the spatial localization is the generation of many

dislocations in a restricted volume. This is possible by the localized Frank–

Read sources or by multiplication at a high stress where the new dislocations

appear near the multiplying ones. Experimental details of plastic instabilities

will be described in Sect. 7.3.

Part II

Dislocation Motion in P articular Materials

205

Part II of the book presents results on a number of selected materials

mainly chosen from experiments performed in the group of the author, when-

ever suitable data, micrographs, and video recordings were available. Thus,

these chapters cannot be considered review articles of the respective classes of

materials. Nevertheless, the selection covers most of the processes controlling

dislocation dynamics in the range of thermal activation, which were described

in Part I. When necessary, the text is supplemented by other data to complete

the view on the particular class of materials. In the elemental semiconductors,

the double-kink or Peierls mechanism controls the dislocation mobility over

a wide range of temperatures (Sect. 6). Ceramic single crystals (Sect. 7) are

partly brittle at low temperatures because of a high Peierls stress. At high tem-

peratures, they may show an athermal behavior and several other mechanisms

governing the dislocation velocity. Pure metals are plastic down to very low

temperatures, but alloying with other elements causes solution and precipita-

tion hardening (Sect. 8). Many intermetallic alloys show a ﬂow stress anomaly,

i.e. an increase in the ﬂow stress with increasing temperature. The anomaly

may be caused by particular conﬁgurations of the dislocation cores but also by

local diﬀusion phenomena (Sect. 9). Finally, quasicrystals are a special case of

intermetallic materials with long-range order but without lattice periodicity.

Here, the structure is described in a higher-dimensional hyperspace, which

determines also the properties of dislocations. However, diﬀusion processes

seem to control the dislocation mobility (Sect. 10). The following chapters

will present the crystal structures of all described materials, their dominat-

ing slip systems, their microscopic and macroscopic deformation properties,

and ﬁnally the processes controlling the dislocation dynamics. If available, the

dislocation motion is illustrated by video sequences accompanying this book.

These video clips are commented in the text. Within the video sequences,

special events are marked by letters or other labels.

It is hoped that the reader who is not very familiar with dislocation prop-

erties will obtain an overview of the processes governing dislocation dynamics

in the diﬀerent materials and that the video sequences and their present

interpretation will stimulate researchers in the ﬁeld to reconsider some of

the established opinions.

Comments on the Video Sequences Available in the Internet

The video sequences can be downloaded via http://extras.springer.com/2010/

978-3-642-03176-2 as a zip archive. Because of the large size of the ﬁle, DSL

is essential. Unpacking the zip ﬁle yields several folders containing the video

ﬁles organized on an internet browser basis. It is recommended to employ

Firefox as the internet browser and the Windows Media Player as the default

player. The videos will also run on a more recent Quicktime player. Viewing

the videos can be started by double-clicking the ﬁle START.html.

In all video recordings, the tensile direction is inclined with respect to

the vertical direction. The angle amounts to 36

◦

in clockwise sense at a

206

magniﬁcation where the frame width corresponds to 6 μm. The angle is slightly

smaller for higher magniﬁcations and larger for lower ones. This relation

between the images and the tensile direction holds also for many micrographs

from in situ experiments but not for all. Sometimes the tensile direction is

indicated. As a measure of the magniﬁcation, the frame width is included in

the titles of the video clips.

In the video recordings, the images of quickly moving dislocations are

blurred due to the afterglow of the luminescence screen, which the videos were

taken from. In many video clips, the place of observation was intentionally

shifted from time to time to follow special events or to move to more active

specimen regions. Besides, it was frequently tried to improve the imaging

conditions by slightly tilting the specimen during the video recording. This is

frequently connected with strong changes in the contrast of the dislocations

and mostly also with a shift of the image position. These manipulations were

done trying to improve the image quality.

If the Burgers vectors of the moving dislocations have a component out of

the specimen surfaces, the dislocations trail a slip step, which requires addi-

tional surface energy causing a drag force on the dislocations. Therefore, the

dislocations may bow out near the surfaces. The same happens if the speci-

mens are covered with a contamination layer, which is mostly the case. Then,

the moving dislocations have to deform the surface layer. This process may

be treated as the creation of dislocations parallel to the surface between the

specimen and the surface layer marking the traces of the moving dislocations.

The elastic strain ﬁelds of the surface dislocations are imaged in the diﬀrac-

tion contrast as so-called slip trails or slip traces. They mark the intersection

lines between the slip planes and the surfaces and can be used to identify slip,

cross slip, and climb as well as to index the slip planes.

For viewing the video clips, it is very useful to employ a video player with

a shuttle control, where it is possible to shift a certain sequence forward and

backward to analyze the process in detail.

Semiconductors

Semiconductor crystals show a strong directional covalent bonding and are

therefore prime examples of the control of the dislocation dynamics by the

double-kink or Peierls mechanism. This is connected with a strong tempera-

ture dependence of the dislocation mobility and the macroscopic ﬂow stress.

At low temperatures, the semiconductor crystals are brittle, like most of the

other materials with a high Peierls stress. After the ﬁrst review by Alexander

and Haasen [279], plastic deformation and dislocation properties have been

summarized in several articles, for example, [357–359]. The knowledge of the

dislocation and plastic properties of semiconductor crystals is important for

the production of electronic devices with their manifold thermal treatments.

As dislocations are mostly detrimental to the operation of devices, respective

production processes have to minimize the number of dislocations in them.

This requires information about dislocation mobility and annealing properties.

6.1 Crystal Structure and Slip Geometry

The elemental semiconductors like silicon and germanium, which are the main

topic of this chapter, crystallize in the cubic diamond structure and many

compound semiconductors in the sphalerite structure. The diamond structure

is built of {111} double layers (a



b, b



c, c



a, etc.) of tetrahedrally coordinated

atoms stacked in an ...ABCABC... sequence like the f.c.c. metals, as shown

in Fig. 6.1 in a projection along [

110]. In the sphalerite structure, the a, b,

c planes are occupied by one sort of atoms, while the a



planes are

occupied by the other one. The {111} planes are also the slip planes with

1/2110 Burgers vectors. Thus, Fig. 6.1 is the projection in the direction of

one of the three Burgers vectors on the (111) plane. In total, there are 12 slip

systems. As outlined in Sect. 4.2.1 and described by (4.19), the Peierls stress

should be small for small Burgers vectors and large interplanar distances.

Dislocations should therefore glide between the widely spaced atom planes aa



,orcc



. These interatomic planes are called the shuﬄe set. In contrast to

208 6 Semiconductors

[111]

Fig. 6.1. [

110] projection of the diamond structure consisting of an ...ABCABC...

stacking of (111) double layers. Thin lines mark single bonds. Thick lines represent

two bonds starting from an atom, one directed forward and the other backward so

that each atom has four bonds in a tetrahedral conﬁguration

that, dislocations moving on the narrow interatomic planes belong to the glide

set. The distinction between the glide and the shuﬄe sets was made in [12].

The interplanar distance of the shuﬄe set is three times that of the glide set.

Weak beam and high resolution TEM indicate that the dislocations dissociate

into Shockley partial dislocations bounding an intrinsic stacking fault on the

plane of the glide set. The reaction is the same as that in f.c.c. crystals (3.50)

outlined in Sect. 3.3.2 [360–364]. In situ TEM studies of dislocations in Si

generated at the edge of the perforation of the specimen show the successive

creation of two partial dislocations [365]. Thus, the dislocations are created

and move in the dissociated conﬁguration on the narrow interatomic planes

of the glide set. The presence of a dislocation in a semiconductor crystal

is connected with broken (dangling) bonds. However, neighboring dangling

bonds saturate to reconstructed covalent bonds. These reconstructions have

to be broken if the dislocation moves.

Because of the action of the Peierls mechanism, the dislocations tend to

orient along the Peierls valleys. These are the most closely packed 110 direc-

tions. Thus, full dislocation loops take the shape of hexagons as illustrated

in Fig. 6.2. The loop consists of two screw segments and four segments of 60

◦

character. The screw segments are split into two partial dislocations of 30

◦

character, while the 60

◦

segments dissociate into a 30

◦

and an edge partial.

According to (3.51), the dissociation width is larger for the 60

◦

segments,

that is, 5.8 nm compared to 3.6 nm for screws in Si, and 3.9 or 2.4 nm, respec-

tively, in Ge [366]. It is assumed that the 30

◦

and 90

◦

partials have diﬀerent

mobilities. In an expanding dislocation loop, two pairs of 60

◦

segments have

a diﬀerent sequence of the leading and trailing partials. The consequences are

a slightly diﬀerent mobility of the respective pairs of segments and a diﬀerent

dissociation width [367].

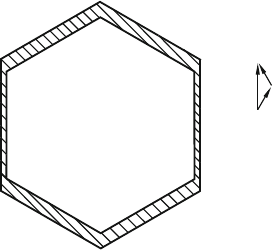
6.2 Microscopic Observations 209

30°

30°30°30°

30°

90°

screwscrew

60°

60°60°

60°

Fig. 6.2. Hexagonal dislocation loop consisting of two Shockley partials comprising

an intrinsic stacking fault

6.2 Microscopic Observations

As discussed above and shown in Fig. 4.6, dislocations at rest in silicon assume

a relatively straight course along the 110 directions, in accordance with the

expectation from the Peierls mechanism. In the corners between the straight

segments, the dislocations may be curved. During their motion, the morphol-

ogy of the dislocations may deviate from the straight shape as illustrated in

the following video clips taken from HVEM in situ straining experiments on

polycrystalline silicon described in [163].

Video 6.1. Dislocation motion in polycrystalline silicon at about 500 and 550

◦

This clip consists of two sequences.

1. 500

◦

C: At this temperature, which is relatively low for silicon, the dislocations

move in an essentially straight conﬁguration oriented along the Peierls valleys

in a steady viscous way. Several dislocations have jogs (angles in the dislo-

cation lines) that impede the dislocation motion and move together with the

dislocations.

2. 550

◦

C: This is an intermediate temperature, where several moving dislocations

are still straight but others are curved. Many moving dislocations are impeded

at their emergence points through the surface and bow out there. On the right

of the blue label A, dislocations move with jogs, which are dragged behind the

main dislocation line. On the right of label B, a jog in a dislocation near the

upper edge of the image trails a dipole.

Video 6.2. Dislocation motion and generation in polycrystalline silicon at about

650

◦

C: At this relatively high temperature, the dislocations move still viscously. In

motion, they are no longer oriented along the Peierls valleys. On the left of the blue

label A, a dislocation moves upwards before it reacts with a ﬁxed straight dislocation

in 45

◦

orientation in the image, where parts of both dislocations are annihilated. It

is supposed that both dislocations are arranged on diﬀerent glide planes but have

the same 1/2110 Burgers vector oriented along the intersection line between both

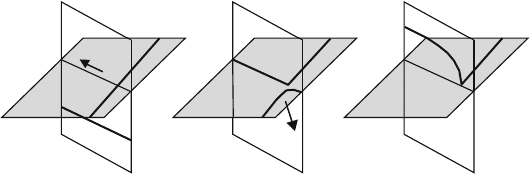
210 6 Semiconductors

(a)

(b) (c)

Fig. 6.3. Formation of a dislocation source by the reaction of two dislocations of

the same Burgers vector

{111} slip planes, as outlined in Fig. 6.3a. When the moving dislocation 1 meets the

ﬁxed one 2 at the intersection line, two angular dislocations may form as sketched

in Fig. 6.3b. One of them marked by an arrow may move out of the specimen. If the

remaining part of the dislocation 1 resumes moving, it is pinned by the rest of the

ﬁxed dislocation 2 at the intersection point. It will bow out as outlined in Fig. 6.3c

and revolve around the pinning point to emit a number of new dislocations.

When the source dislocation stops moving after label B, the curvature disappears

and the dislocation at rest orients again along a Peierls valley.

A series of in situ experiments have been performed on pure germanium

and Ge–Si solid solutions [368]. On the one hand was Ge alloyed with 4% Si,

and on the other was Si with 5% Ge. The crystals were predeformed to reduce

their brittleness. All specimens had (111) foil surfaces. They were deformed

along 123. Qualitatively, the alloying changes the dislocation behavior only

little so that these experiments give some additional information on the gen-

eral dislocation behavior in the elemental semiconductors. However, as will be

described later, the mobility of the dislocations is reduced with respect to the

pure elements so that the deformation conditions change. The following two

clips present pure Ge. In accordance with the lower melting point of Ge with

respect to Si, the deformation temperatures are also lower than those of Si.

Video 6.3. Several slip bands in Ge at about 430

◦

C: The quality of this clip is

poor because of strong adjustments of the imaging conditions during recording.

Nevertheless, the clip shows at this low temperature that only part of the dislocations

move in the straight oriented conﬁguration.

Video 6.4. Motion of dislocations in a dislocation network in Ge at about 610

◦

In pure Ge at an intermediate temperature, dislocations in a relatively dense network

move in curved conﬁgurations. This underlines the observation that dislocations

mostly do not move in the straight shape predicted by the Peierls model.

The next video shows a sequence of the Ge-4 at% Si alloy. As it will be

described in Sect. 6.5, the alloying increases the ﬂow stress so that the ade-

quate deformation temperatures are higher than those of the pure elements.

6.2 Microscopic Observations 211

Video 6.5. Dislocation band in a network in Ge-4 at% Si at about 655

◦

C: In this

sequence, moving dislocations are slightly pinned at the emergence points through

the surface and bow out in-between. It was shown in the Video 6.2 that disloca-

tions in semiconductor crystals are generated by localized sources. Here, dislocations

emitted from a source on the right of the imaged area move in a collective way in a

narrow slip band. The collective behavior mainly results from the elastic interactions

between the piled dislocations in the band.

In the Si-5%Ge alloy, the deformation temperatures are higher than in

Ge, as stated earlier. The slip geometry and the shape of dislocations in the

partly unloaded state are demonstrated in Fig. 6.4 taken at diﬀerent temper-

atures. The slip geometry is indicated in Fig. 6.4b. There are two traces of

slip planes, trace 1 along [01

1] and trace 2 along [

110]. Burgers vectors of

these directions have the highest orientation factors of 0.47 and 0.29. The

two shorter edges of the triangles mark the projections of the other two 110

directions on the respective slip planes. Thus, dislocations along these direc-

tions like the dislocations a and a



in Fig. 6.4b should be 60

◦

dislocations.

These are the dislocations mainly moving in the following video sequences. The

straight dislocation segments labeled a and b in Fig. 6.4a belong to the slip

systems 1 and 2 and are of screw character. They are less mobile than 60

◦

and mixed segments, so that they are dragged by them.

The following videos are from the same in situ straining experiment.

Video 6.6. Dislocation bands in Si-5 at% Ge at about 745

◦

C: This clip consists of

three sequences of neighbored specimen areas taken under very similar conditions.

1. Dislocations move in two slip bands with traces 1 and 2 at an intermediate

temperature at a relatively high speed. The images of the moving dislocations

are therefore blurred by the afterglow of the luminescent screen of the recording

system. According to the high stress corresponding to the high speed, many

dislocations are quite straight, especially when they are at rest. The dislocation

at A is a forest dislocation for the dislocations of slip system 2. The disloca-

tions of the latter system are pinned temporarily and wind around the forest

dislocation, showing that the forest dislocations are strong obstacles.

2. This sequence continues the foregoing one. Above B is an obstacle, probably a

forest dislocation arranged approximately end-on. Dislocations interacting with

the obstacle acquire a jog with the adjacent segments strongly bowing out.

3. In the lower part of the last sequence, a dislocation moving from left to right is

impeded by other dislocations. It forms a localized dislocation source emitting

some new dislocations.

Video 6.7. Dislocation band in Si-5 at% Ge at about 835

◦

C: The clip shows the

same specimen as before at a high temperature. The dislocations in the slip band

are pinned by many jogs, which are most probably formed by cross slip as described

in Sects. 5.1.1 and 5.1.2 (Fig. 5.5). During the motion, the jogs glide along the dislo-

cations in the direction of the Burgers vector, marked by the blue line. The segments

between the jogs bow out, indicating that jogs performing a combined conservative

motion in forward direction and sidewise along the dislocations represent obstacles

to the dislocation motion. In some places, debris (small dislocation dipole loops) is

left, for example, at A.