Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

232 7 Ceramic Single Crystals

foil plane, and oblique slip bands extending in [110] or [1

10] directions have

1/2110 Burgers vectors in the foil plane. Dislocations moving during in situ

experiments in oblique slip bands are presented in Fig. 7.7. The specimens are

tilted around an axis parallel to the extension of the bands to look onto the slip

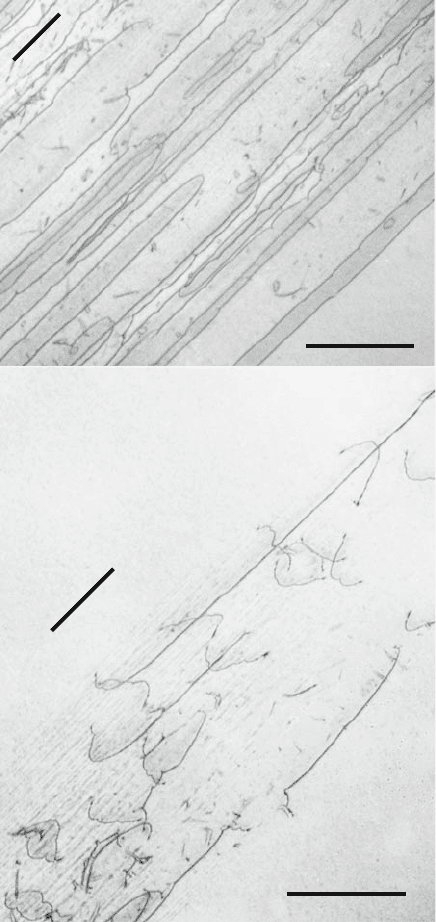
planes oriented edge-on in the specimens. Figure 7.7a shows an oblique slip

band with edge dislocation segments E trailing long screw segments S, thus

forming very elongated dislocation loops. This indicates a higher mobility

of edge dislocations as observed in most materials, for example, in LiF in

Fig. 4.41. Screw dislocations can well be observed in orthogonal slip bands

as in Fig. 7.8. In these bands, the traveling distance of the edge dislocations

is limited by the foil thickness so that they escape through the surface. The

screw dislocations are strongly pinned by the localized obstacles and bow

out between them as illustrated before in Fig. 4.13. The deep cusps in the

dislocation line as, for example, J in Fig. 4.13, originate from jogs formed

by cross slip trailing dipoles (Sect. 5.1.2). Cusps are also observed in moving

edge dislocations, c.f. Fig. 7.7b. They may also be due to localized obstacles

or to the drag caused by jogs moving conservatively (Sect. 4.8, Fig. 4.31). In

the orthogonal slip bands as in Fig. 7.8, edge segments do sometimes not

show the curly shape of locally pinned dislocations but exhibit quite straight

segments connected by superkinks. This points at the additional action of the

Peierls mechanism. The double-exposure of the dislocation line marked by an

arrow indicates that the superkinks do not move smoothly as predicted by the

Peierls mechanism. They rather move in jumps. Thus, the kinks are stabilized

by localized obstacles. After their overcoming, the kinks move quickly into a

new pinned position. Within the slip bands, the dislocation densities typically

amount to 1.5 ×10

−2

.Withα

= π in (5.11) and a shear modulus of μ =

124 GPa, this yields an athermal component of the ﬂow stress of τ

≈ 23 MPa.

Many of the kinematic features of the jerky motion of dislocations in MgO

are well illustrated by the following two video sequences. The ﬁrst one also

illuminates all the processes involved in the generation of dislocations by the

double-cross slip mechanism (Sects. 5.1.1 and 5.1.2 and the ﬁgures therein).

Video 7.1. Dislocation motion and generation in MgO single crystals at room tem-

perature: This video clip is of low quality. As the original record is lost, the present

clip is a copy of a 16 mm movie taken from the original recording. Nevertheless, this

sequence shows many processes in a clear way. The projection of the Burgers vector

is indicated by the red line b. Owing to the pinning by localized obstacles, the dislo-

cations move in a jerky way, usually by jumps of segments of the order of magnitude

of the obstacle spacings. Many processes visible are related to the motion of jogs,

the trailing of dislocation dipoles, and the double-cross slip multiplication mecha-

nism. At C, jogs in a screw dislocation move conservatively along the dislocations. A

multiplication event starts at M by forming a loop at a jog. Later, the loop increases

in size and forms two new dislocations. At L, another dislocation loop develops at

a jog. Much later, it is growing to a large loop before it further develops into two

new dislocations at MM. Jogs JE in edge dislocations move conservatively with the

dislocation. Nevertheless, they form cusps indicating an increased lattice friction,

owing to the Peierls mechanism acting simultaneously. A small loop collapses at SL.

Many of these processes occur simultaneously in all regions of the image.

7.2 Magnesium Oxide 233

1 µm

(a)

1 µm

(b)

Fig. 7.7. Oblique slip bands in MgO single crystals during in situ deformation in

the HVEM at room temperature. Trailing of long screw dislocations by moving edge

dislocations (a). Moving edge dislocations (b). The specimens are tilted by about

◦

away from the [001] foil normal in [1

10] direction. Tensile direction vertical, b

Burgers vector. From the work in [281]

234 7 Ceramic Single Crystals

0.5 μm

Fig. 7.8. Slip band in an MgO single crystal during in situ deformation in the

HVEM at room temperature. Tensile direction vertical, b projection of Burgers

vector. From the work in [281]

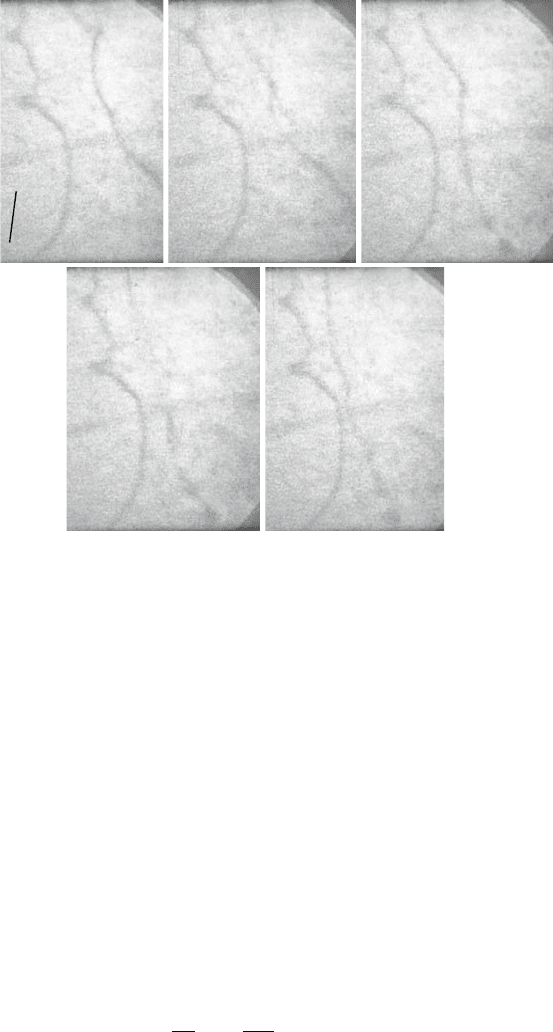
Video 7.2. Motion of a dislocation in MgO at room temperature: At high mag-

niﬁcation, details can be observed of the motion of a dislocation in an array of

local obstacles in MgO. The screw dislocation is pinned locally. Between the stable

positions, it moves at diﬀerent velocities. Sometimes, the dislocation jumps to the

next stable position during the time interval between successive frames. In Fig. 7.9a,

taken from this video sequence, the dislocation is pinned in a stable position. After

thermal activation in the next frame (in b), the dislocation is imaged in several posi-

tions in a blurred way. It reaches the next stable position in (c). The same repeats

in the next two frames (d, e). By shuttling from frame to frame, the transition

between stable and very dynamic states canbeobservedseveraltimeswithinthis

sequence. Frequently, however, the dislocation moves also in a smooth way, again

indicating the action of the Peierls mechanism. A jog marked by a deeper cusp in

the dislocation line at C moves conservatively along the dislocation.

Apparently, the motion of dislocations in MgO at room temperature is con-

trolled by both the localized obstacles and the Peierls mechanism. As discussed

in Sect. 4.6, the relative signiﬁcance of both processes can be judged by com-

paring the waiting times t

at the obstacles with the traveling times t

between

them. In the Video 7.2 showing a dislocation just in motion, both are of the

same order of magnitude. In general, however, as in Video 7.1, most disloca-

tions do not move temporarily, pointing at long waiting times at the obstacles.

Observing the specimen area over a long time illustrates that practically all

dislocations are mobile. Thus, it may be justiﬁed to evaluate the dislocation

motion mainly in terms of localized obstacles but considering also the Peierls

mechanism.

7.2.2 Statistics of Overcoming Localized Obstacles

Micrographs from the in situ straining experiments on MgO crystals oﬀered the

unique opportunity to determine the statistical properties of the interaction

7.2 Magnesium Oxide 235

(a) (b) (c)

(d)

(e)

Fig. 7.9. Successive frames of the motion of a dislocation in MgO at room

temperature at high magniﬁcation. From the work in [281]

between dislocations and localized obstacles, that is, the frequency distribu-

tions of the forces acting upon the obstacles, the obstacle distances (segment

lengths), and the local eﬀective stresses. Positive copies of the micrographs

were projected onto the screen of a digitizer. The bowed dislocation segments

were visually compared with ellipses of diﬀerent sizes calculated by isotropic

line tension theory according to the anisotropic energy factors of edge and

screw dislocations in MgO. The measuring procedure [101] consisted in digi-

tizing the position of a cusp in the dislocation line representing an obstacle,

ﬁtting an ellipse of suitable size to the adjoining dislocation segment and

repeating this procedure along the dislocation line. The obstacle distances are

the distances between the cusps, and the forces on the obstacles were calcu-

lated from the vector sum of the line tensions of the segments neighboring the

obstacles (3.39), Γ = E

(1 + ν − 3ν sin

β), where β is the orientation angle

of the dislocation arcs touching the obstacle. In the respective line tension

approximation, the local eﬀective stress is given by (5.18)

∗

S =

(ln (l/r

)+C) S. (7.3)

236 7 Ceramic Single Crystals

S = x

−1

= e

−1

is the reciprocal major half-axis of the ﬁtting ellipses

(Sect. 3.2.7).

The experimental distributions of the forces and obstacle distances were

ﬁrst published in [102, 405] and compared with the results of computer sim-

ulations of thermally activated dislocation motion in the ﬁeld of Fleischer

type obstacles in [406] as mentioned above in Sect. 4.5. In the simulations, the

bowed dislocation segments were treated in the approximation of constant line

tension, that is, of constant radius of curvature r.Itisdiscussedin[406]that

for low forces f

< 0.7 and low applied stresses τ



/τ



< 0.3 ...0.4 (i.e., ther-

mal activation at all obstacles), the frequency distributions can be normalized

also in the thermally activated case according to the scaling laws

g(f)

R,l

= AG(Af)=AG(u)

h(l)

R,l

= BH(Bl)=BH(v),

with

u = Af and v = Bl

and the scaling factors

A =(2/(3τ

2

))

1/3

and B = l

−1

(2τ



/3)

1/3

. (7.4)

Accordingly, the averages of the physical and normalized quantities are

related by



∞

uG(u)du = u = Af



∞

vH(v)dv = v = Bl (7.5)

To normalize the experimental histograms g(f)andh(l), the scaling factors

may be derived from the experimental and theoretical averages. Special com-

puter runs were performed to satisfy the experimental conditions as best as

the available computer program allowed. This included the choice of the tem-

perature and the dislocation length, the latter of which inﬂuences the shape of

the distributions. The average values slightly decrease with increasing recip-

rocal temperature and dislocation length but they do not depend on the

stress for τ



/τ



< 0.35 and f

< 0.7. In the present case, u = v =0.71.

Figure 7.10 presents the result of the comparison between the experimental

and theoretical distributions.

For the evaluations, a set of micrographs was chosen showing the same

specimen area, with the applied stress increasing from 6.06 to 8.06 (in rel-

ative units). More than 200 segments were measured for each micrograph.

The theoretical histograms correspond to “short” dislocations, that is, those

containing 20 segments. This length agrees with the length of dislocations in

the foil specimens. The histograms for short dislocations resemble the experi-

mental distributions more closely than those for long dislocations, calculated

7.2 Magnesium Oxide 237

Fig. 7.10. Frequency distributions of the normalized distributions of forces acting

on the obstacles (a) and obstacle distances (b) in an MgO single crystal. His-

tograms: result of computer simulation; data points: results from in situ experiments.

Stresses applied to the tensile specimen in relative units: squares 6.06, diamonds 6.22,

downward triangles 7.21, circles 7.95, upward triangles 8.06. Data from [406]

before also by other authors [194, 198]. According to [407], the maximum is

always at about u =0.8 for intermediate temperatures.

The theoretical force distribution follows the schematic shape shown in

Fig. 4.17, except that at high forces the tail is longer. The experimental and

theoretical force distributions resemble each other, but show also character-

istic diﬀerences. In particular, the maximum of the experimental distribution

is shifted to lower forces, which may have several reasons. While some

parameters of the simulation agree with those of the experiment as, for exam-

ple, the temperature and the relative stress τ



/τ



≈ 0.28, the strength of the

obstacles is quite diﬀerent, f

=0.26 in the simulation and f

≈ 0.8inthe

experiment, where for f

approximately the upper bound of the force dis-

tribution is used, which certainly is an overestimate. Besides, the resolution

power of the electron micrographs is limited, resulting in a decrease of the

frequencies of small obstacle distances and forces. Nevertheless, it is not very

probable that these eﬀects caused the deviations between the histograms from

the simulations and the experimental results. A main reason for this diﬀerence

will be the assumption of a single type of obstacles for the calculations and

the presence of a spectrum of obstacle strengths and sizes in the experiments,

which leads to a shift of the maximum to lower forces and to a longer tail

after the maximum. The obstacle spectrum will be discussed in Sect. 7.2.5.

The segment length distribution has a typical asymmetric shape. This can

be used to discuss the mechanisms causing the length distributions in other

materials. According to the theory, the average obstacle distances depend on

the acting stress according to the Friedel relation (4.53) or (4.54), respectively.

With the normalizing relations for the case of thermal activation (7.4) and

(7.5), and r equal to 1/S,itreads

l = vl

(2τ



/3)

−1/3

=0.812 l

2/3

(S/2)

−1/3

, (7.6)

238 7 Ceramic Single Crystals

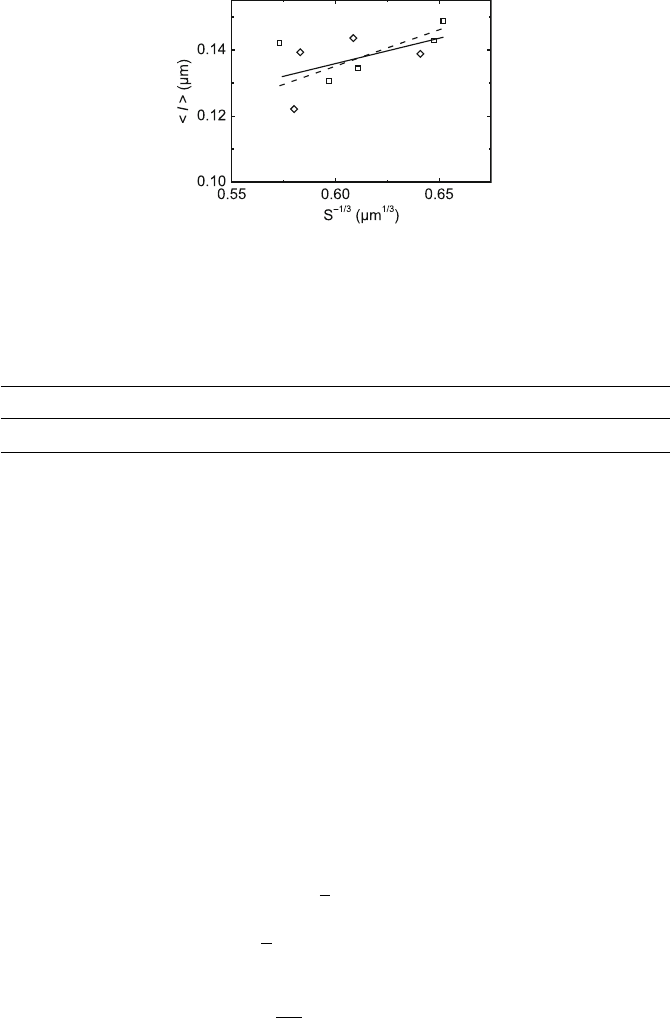
Fig. 7.11. Dependence of the average obstacle distance on the dislocation curvature

according to the Friedel relation for two series of load changes during in situ straining

of MgO. Data from [204]

Table 7.2. Average obstacle data for an MgO single crystal from an in situ straining

experiment at a relative stress of 7.95

F l (μm) 1/S (μm) l

(μm) l

/b r (μm) τ



0.273 0.130 0.213 0.093 320 0.239 0.22

Measured from micrograph: F  force, l segment length, 1/S dislocation curva-

ture. Calculated from distributions by (7.4) and (7.5): l

square lattice distance, r

radius of curvature of segments, τ



normalized eﬀective stress. Data from [406]

which only slightly diﬀers from (4.53). Figure 7.11 presents the respective plot

for two independent series of load changes during in situ straining. The full

line is a linear regression including an intercept. The correlation coeﬃcient of

0.57 yields a conﬁdence probability of the correlation of 95%. The dashed line

meets the origin and, apart from a slight diﬀerence in the numerical constant,

it represents the Friedel relation. According to the author’s knowledge, there

is no other microscopic evidence of the Friedel relation.

Table 7.2 presents average values of the parameters of the distributions at

the relative stress of 7.95. Equations (7.4) and (7.5) and τ



= l

/(2r)were

applied to calculate these values. The data at diﬀerent stresses proved the

constancy of the square lattice distance l

≈ 320 b except at the highest stress

where the dislocations had moved considerably. The small diﬀerence between

l and l

results from the high strength of the obstacles and the related strong

bowing of the dislocation segments. l

deﬁnes an eﬀective concentration of the

obstacles on the slip plane via b

√

). With the obstacles having a width

w,eachofthemactsonw/b slip planes so that the number of obstacles per

lattice site becomes c = b

√

2wl

). As it will be discussed in Sect. 7.2.5, the

obstacles are supposed to be spinel particles of octahedral shape. Then, the

edge length w can be expressed by l

, and the total concentration of trivalent

impurities c

via w =2

1/4

√

.Withc

= 300 ppm, w amounts to 12b.

With this small size and high strength of the obstacles, the necessary condition

for applying Friedel statistics (4.52) is fulﬁlled, ξ

=(x

−1/2

=0.04  1.

7.2 Magnesium Oxide 239

As it is expected, the values of S representing the eﬀective stress τ

∗

increase

with increasing applied stress as discussed in Sect. 5.2.3. The relation between

∗

and τ was demonstrated in Fig. 5.28. The dependence of the dislocation

curvature on the segment length being a consequence of the dislocation self-

interaction was plotted in Fig. 3.21. In contrast to the computer simulations

with a constant radius of curvature of the dislocation segments, the values

of S show a relatively wide symmetric distribution with a standard deviation

ΔS of the individual values slightly increasing with increasing S,thatis,

ΔS ≈ (0.7+0.2 S) μm

−1

. This spread of dislocation curvatures is only partly

due to the spatially varying internal stress but results also from the dislocation

self-interaction. Measurements of the dislocation curvature as a probe of the

local eﬀective stress to study the stress distribution around a crack in MgO

under load [408] will be described in Sect. 7.2.6.

7.2.3 Kinematics of Overcoming Localized Obstacles

The video recordings of the dislocation motion also yield information on the

kinematic dislocation behavior. The theory of thermal activation as treated

in Sect. 4.1 describes the waiting time of the dislocation at an obstacle in

dependence on the acting force on the condition that the segments adjoin-

ing the obstacle do not change their positions. When a certain obstacle is

surmounted, however, the dislocation position changes at both neighboring

obstacles so that the time t

the dislocation is in contact with an obstacle

is usually not identical with its waiting time. t

is called the lifetime of the

obstacle at the dislocation. The distribution of the lifetimes, which is related

to the obstacle spectrum, deﬁnes the jerkiness of the dislocation motion as

well as the average dislocation velocity. Although this distribution can easily

be obtained from computer simulations, experimental data are very scarce.

Because of the diﬀerent lifetimes at the individual obstacles, the dislocations

do not advance simultaneously over their whole length. Frequency distribu-

tions of the local slip distances in dependence on the observation time intervals

contain information on the spatial arrangement of the obstacles.

For kinematic evaluations, photographs were taken from the video screen

in a ﬁxed time sequence. To evaluate numerical data, a copy of one state was

superimposed onto another one of the state after a certain observation time t

An example is given in Fig. 7.12. Pairs of points on dislocations in the initial

and ﬁnal positions were measured by a coordinate digitizer dividing the swept

area into tetragons. On resting dislocation segments, the same points were

digitized twice. The following quantities were calculated: the segment length λ

belonging to a single tetragon i as the average of the lengths in both positions,

and the total dislocation length λ

;theareaΔA

of the single tetragons, and

the total area A swept during t

; the local slip distances p

=ΔA

/λ

,andtheir

average during t

; and ﬁnally, the length of dislocations λ

moving during

. Segments resting during t

are characterized by p

= 0. The evaluations

comprised a specimen region of Video 7.1 in which mainly screw dislocations

240 7 Ceramic Single Crystals

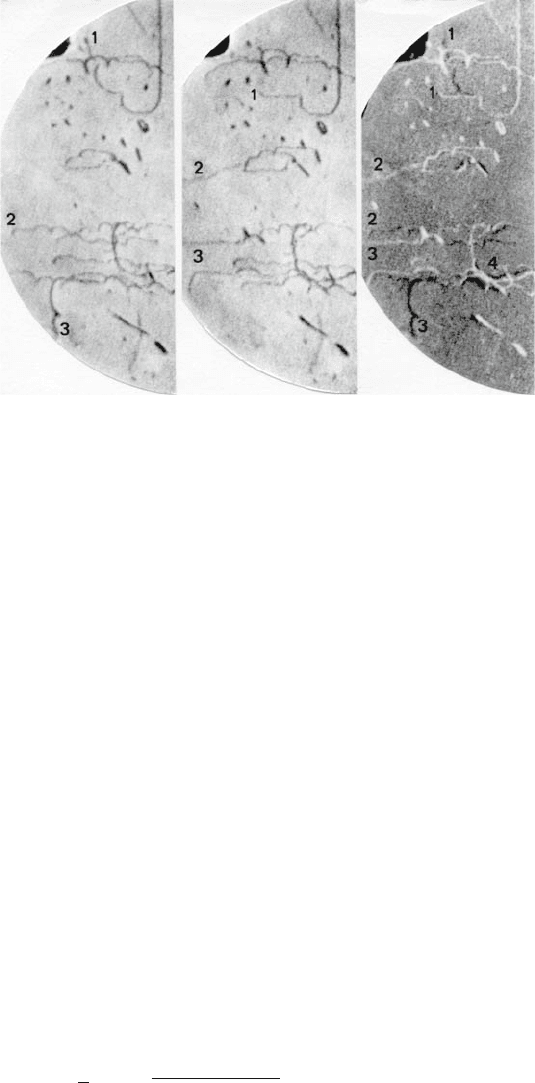
Fig. 7.12. Two stages of dislocation motion in MgO taken from the Video 7.1. Left:

initial state. Middle: state after t

. Right: superposition of the initial and subse-

quent states, the latter as a negative. Moving dislocations appear as dark and bright

lines, resting ones are imaged with reduced contrast. From [409]. Copyright (1988)

Pergamon Press, Oxford

of 19 μm in length moved for 110 s as well as a slip band with dislocations of

a large edge component of 33 μm in length observed for 18 s.

The total swept area proved to be proportional to the observation time,

indicating a homogeneous dislocation motion in the observed specimen region

of the screw band at an area velocity of

A =0.13 μm

−1

and an average dis-

location velocity of v

A/λ

=7×10

−9

−1

corresponding to a local strain

rate of 6 × 10

−6

−1

. The frequency distributions of the slip distances in the

screw band are plotted in Fig. 7.13 for four diﬀerent observation times t

.For

short t

, the frequencies rapidly decrease with increasing slip distances. After

about 10 s, a maximum appears at about p =0.35 μm. A second maximum

occurs at p =0.85 μm after longer times.

For a single type of localized obstacles, something like a Poisson distribu-

tion may be expected theoretically, with the maximum continuously shifting

towards larger p with increasing t

. The occurrence of maxima in ﬁxed posi-

tions points at a preference of certain slip distances. The smallest preferred

distance should be the square lattice distance l

, determined to be 0.093 μm

in the preceding section. This distance is represented by its high frequen-

cies for short observation times. From the shape of the force distribution in

Fig. 7.10a, it was concluded that the obstacles are not of unique type. The

preferred slip distance of 0.35 μm may therefore correspond to the distances

between few of strong localized obstacles. The second maximum at 0.85 μm

can be interpreted as the wavelength of the long-range stress ﬁelds of the

dislocations 1/

√

 =1/

√

1.5 × 10

−2

≈ 8 × 10

−7

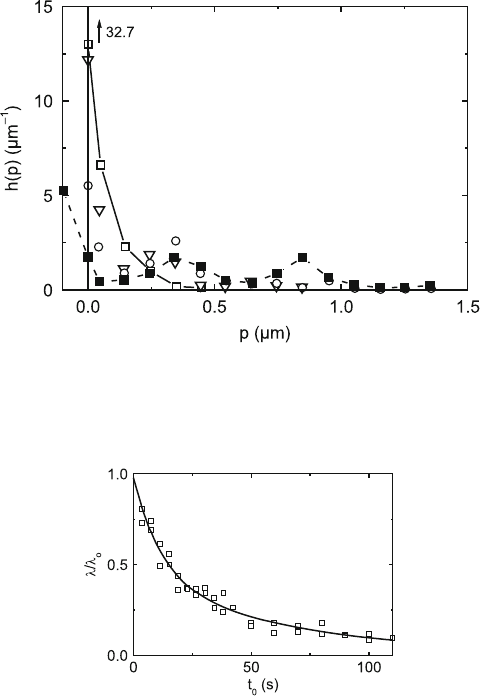
7.2 Magnesium Oxide 241

Fig. 7.13. Frequency distribution of slip distances in a screw dislocation band

for diﬀerent observation times. t

=3.9s (open squares), 11.6 s (triangles), 30.8 s

(circles), 100 s (full squares). Data point at negative p: dislocation segments which

had moved out of the frame. Data from [409]

Fig. 7.14. Dependence of the relative length of resting dislocations on the

observation time in a screw band in MgO. Data from [409]

A certain part of the total dislocation length does not move during an

observation time interval t

. This resting length λ

= λ

−λ

decreases with

increasing t

as plotted in Fig. 7.14 for the screw band. The decrease down to a

low value indicates that in the observed specimen region almost all dislocations

are mobile. The decrease can well be described by two exponentials with

diﬀerent time constants

)/λ

= C

exp(−B

)+C

exp(−B

), (7.7)

with B

=0.0909 s

−1

and B

=0.0155 s

−1

. There ought to be a theoretical

connection between the dependence of λ

)/λ

and the frequency distribu-

tion of the lifetimes h(t

). Several proposals [204,410,411] have been discussed

in [204] but a coherent theoretical formulation is still missing. According