Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

242 7 Ceramic Single Crystals

to [410], the fraction of dislocations not moving during t

is given by the

cumulated frequency of the lifetimes with t

≥ t

)/λ



∞

h(t

)dt

After computer simulation experiments, the cumulated frequency is given

by an exponential function decreasing with t

for long dislocations at high

temperatures. For short dislocations at low temperatures, the course can be

described by the sum of two exponentials as found experimentally in (7.7).

By diﬀerentiation, there follows that

h(t

)=B

exp(−B

)+B

exp(−B

In all the models, the time constants in (7.7) equal the reciprocal lifetimes.

The existence of two lifetimes again indicates the occurrence of a spectrum of

obstacles of diﬀerent strengths.

The mode of dislocation motion observed experimentally where most

obstacles are overcome individually but some are passed spontaneously allows

conclusions to be drawn on the relation between the acting eﬀective stress τ

∗

and the athermal stress τ

necessary to surmount the obstacle array without

thermal activation, or between the normalized quantities τ



and τ



, respec-

tively. It follows from Fig. 4.18 that then τ



≈ 3 τ



,orwithτ



=0.22 from

Table 7.2 that τ



≈ 0.66. This agrees with the estimation of f

≈ 0.8from

Sect. 7.2.2 and (4.57), which is quite a high strength.

In conclusion, in situ deformation of MgO single crystals with aliovalent

impurities reveals a wealth of detailed information on the statistics and kine-

matics of the motion of dislocations in the ﬁeld of localized obstacles obeying

Friedel statistics.

7.2.4 Dislocation Dynamics

The stress and temperature dependence of the dislocation velocity in nomi-

nally pure crystals and crystals doped with 150 ppm Fe

was measured in

[403] at and above room temperature using the stress pulse etching technique.

In the pure crystals, the stress exponent m varied between 3 and 6.5, depend-

ing on the oxidation state. The doped crystals were annealed and quenched

to solve the impurities. The stress exponent was then about 11. The edge

dislocations turned out to be much more mobile than screws with stresses to

reach dislocation velocities near 10

−6

−1

of about 10 and 15 MPa. Simi-

lar measurements were carried out on the same more impure material used

also for the other data in this section [412]. Problematic were the large slip

distances of edge dislocations above 100 K, which interfered with the screw

dislocations so that the latter could not be identiﬁed. Therefore, the velocity

of head dislocations in screw bands was determined additionally. As discussed

in Sect. 5.1.1, head dislocations move faster than individual ones under the

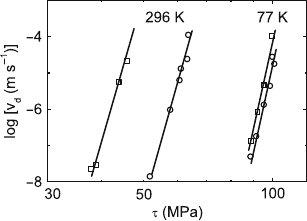
7.2 Magnesium Oxide 243

Fig. 7.15. Stress dependence of the velocity of head dislocations in slip bands in

MgO. Edge dislocations (squares), screw dislocations (circles). Data from [413]

same stress. For the present material, the velocity ratio was less than 10, cor-

responding to only a small shift in the stress. The data at room temperature

and 77 K are plotted in Fig. 7.15. The slope of the curves represents the stress

exponent m = ∂ ln v

/∂ ln τ. For screw dislocations at 77 K, it amounts to

almost 50. Similar values result for the other conditions. The ﬁgure veriﬁes

the great diﬀerence between the mobility of edge and screw dislocations, par-

ticularly at room temperature. This leads to the formation of loops with very

long screw dislocations, which ﬁnally control the ﬂow stress. Elongated loops

were also observed in the in situ experiments in the oblique slip bands where

the edge components do not move out of the foil (Fig. 7.7).

For comparing the results of the velocity measurements with those of

macroscopic deformation tests, some parameters of both methods were plotted

together. In Fig. 7.16, the temperature dependence of the stress necessary to

reach a velocity of individual edge dislocations of v

=10

−7

−1

is plotted

together with the macroscopic yield stress. This dislocation velocity corre-

sponds to that in macroscopic experiments at a strain rate of 10

−4

−1

and a

dislocation density of 1.5×10

−2

quoted before. Both data sets ﬁt well the

same curve. The activation volume was calculated by V = kT (∂ ln v

/∂τ)

Figure 7.17 compares the data with those of the macroscopic tests, revealing

a satisfactory agreement.

7.2.5 Macroscopic Deformation Properties and Discussion

The temperature dependence of the yield stress of the MgO crystals (Fig. 7.16)

shows three ranges: a steep decrease at low temperatures, a more moderate

decrease between about 100 and 750 K, and a plateau above this temperature.

These ranges are explained by the dominance of the Peierls mechanism at

low temperatures, by the interaction with localized obstacles at intermediate

temperatures, and by long-range dislocation interactions at high ones. The

values of the stresses to reach a velocity of edge dislocations of 10

−7

−1

are

slightly lower. Considering the diﬀerence between the mobilities of edge and

screw dislocations suggests that the respective stresses for screw dislocations

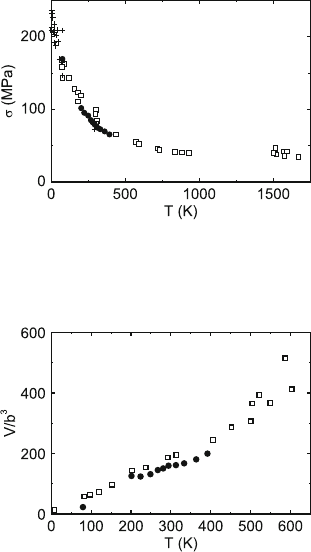
244 7 Ceramic Single Crystals

Fig. 7.16. Yield stress of MgO single crystals with data from [414] (open squares)

and [415] (crosses) as well as stress to reach the velocity of edge dislocations of

−7

−1

(full circles), data from [413]

Fig. 7.17. Activation volume in MgO from macroscopic deformation tests [414]

(open squares) and from measurements of the velocity of individual edge dislocations

[413] (solid circles)

should be much higher. Nevertheless, screw dislocations are considered to

control the deformation over a wide range of intermediate temperatures.

The strain rate sensitivity was measured by strain rate cycling and stress

relaxation tests. It amounts to about r =0.8 MPa near helium tempera-

ture, but it is constant at the low value of 1.5 MPa over a very wide

temperature range between liquid nitrogen temperature and 600 K. Above

this temperature it decreases again. Accordingly, the activation volume is

almost proportional to the temperature as plotted in Fig. 7.17. Reference

[413] contains also measurements of the activation enthalpy by a combina-

tion of temperature and strain rate change tests between about 77 and 600 K

and the resulting Gibbs free energy calculated by (4.15). The latter is pro-

portional to the temperature with ΔG/T =2.17 × 10

−3

eV K

−1

as quoted

before. This proportionality is a necessary prerequisite to the validity of the

Arrhenius equation if the deformation mechanism does not change within the

temperature interval.

The low-temperature deformation data can be analyzed in terms of the

Peierls mechanism. The motion of edge dislocations by the double kink

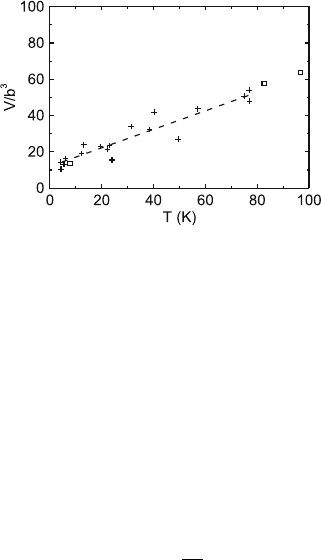
7.2 Magnesium Oxide 245

Fig. 7.18. Activation volume in MgO from macroscopic deformation tests at low

temperatures. Data from [414] (squares) and from [415] (crosses)

mechanism was studied by means of atomistic models in [114, 133], yield-

ing Peierls stresses τ

of the order of magnitude of 90–150MPa and activation

volumes of 60 b

to 120 b

(quoted from [415]). τ

agrees well with the yield

stress extrapolated to zero K of σ =2τ ≈ 250 MPa. Also the experimental

activation volumes at low temperatures plotted in Fig. 7.18 are well within

the range of the theoretical expectation.

After the continuum model in [151], the temperature dependence of the

yield stress in the Peierls region can be described by

τ = τ



1 −





1/2



where τ

is the ﬂow stress at zero temperature and T

the temperature at

which the Peierls mechanism vanishes. The corresponding plot is shown in

Fig. 7.19, yielding T

= 574 K, which means that the double kink mechanism

should act still far above room temperature. This plot does not consider the

athermal stress contribution τ

so that T

should be lower. The dislocation

velocity measurements in nominally pure MgO in [403] are also interpreted

by the Peierls mechanism. The shear stress to move screw dislocations at room

temperature at a velocity of 10

−7

−1

amounts to about 5 MPa in contrast

to a much higher shear ﬂow stress of about 45 MPa. However, the microstruc-

tural observations described in Sect. 7.2.1 also hint at this mechanism, the

occurrence of straight crystallographically oriented edge dislocations and the

viscous motion of screw dislocations between localized obstacles.

However, there is clear microstructural evidence that the overcoming of

localized obstacles dominates the dislocation motion at room temperature

(Fig. 4.13 and Sect. 7.2.1). This is in accordance with the high activation vol-

ume of the order of 200 b

or of the corresponding stress exponent of m



≈ 60.

A model explaining many of the observed features was suggested by Reppich

and Knoch [218, 416]. According to them and the literature quoted, in crys-

tals doped with Fe in the 1,000 ppm range, particles of an octahedral shape

with {111} habit planes form, having an inverse spinel structure. The particles

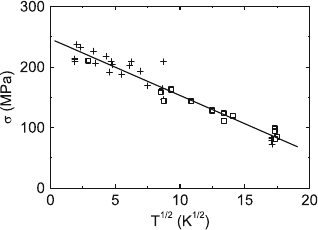
246 7 Ceramic Single Crystals

Fig. 7.19. Temperature dependence of the yield stress according to the model of the

double kink mechanism in [151]. Data from [414] (squares) and from [415] (crosses)

are incorporated coherently. During the cutting of the particles, an antiphase

boundary (APB) has to be formed. The energy required represents the main

obstacle friction mechanism. It is suggested here that the localized obstacles

observed in the TEM and during the in situ investigations consist of these

octahedral particles. The mechanism was discussed already in Sect. 4.7. The

shape of the cutting plane is demonstrated in Fig. 4.26 with the coordinates

being chosen for the intersection by an edge dislocation. For the cutting by

a screw dislocation, the particle has to be rotated by 90

◦

. If the obstacle

resistance is given only by the fault energy γ

APB

, the obstacle force amounts

to F = γ

APB

2z,wherez is half the width at the actual force, and the acti-

vation distance equals the diﬀerence between the equilibrium x values at the

entrance and exit sides Δd = x

−x

. The outline of the particle cutting plane

represents the central cut and the hatched area an “average” oﬀ-center cut.

The noncentral cuts form a spectrum of varying particle widths. The situation

is diﬀerent for edge and screw dislocations as illustrated by the force–distance

curves in Fig. 7.20. At the central cut, edge dislocations experience the larger

maximum force F

in accordance with the larger maximum width. The non-

central cuts generate a spectrum of diﬀerent obstacle strengths because of

the diﬀerent widths in z direction. The average obstacle has the strength

= F

/2. All particles have the same maximum activation distance Δd

The central cut for screw dislocations has a lower maximum force F

than

that of edge dislocations, but all noncentral cuts exhibit the same maximum

strength. The varying quantity is now the activation distance. The “average”

obstacle has the width Δd

=Δd

/2. Thus, while a few particles form strong

obstacles to edge dislocations, many particles cut oﬀ-center have low strengths

and may be overcome spontaneously. For screw dislocations, the particles all

have the same strength, though they have diﬀerent activation distances and

energies. These features may explain why screw dislocations are pinned by

localized obstacles with small obstacle distances, while edge dislocations are

pinned having larger segment lengths, resulting in a higher mobility.

It is diﬃcult to analytically describe the trapezoid shape of the “aver-

age” obstacle interaction potential. The potentials are therefore approximated

7.2 Magnesium Oxide 247

Δd

Fig. 7.20. Force–distance curves for particles of octahedral shape interacting with

dislocations by the formation of antiphase boundaries inside the particles. Inter-

action potential of an “average” obstacle for screw dislocations (thick solid line),

for edge dislocations (thin solid line). Curves for the central cut with maximum

interaction parameters (dotted curves)

by the simple box potential with a constant activation distance Δd.This

approximation is certainly not too bad for screw dislocations controlling the

deformation rate. The Gibbs free energy of activation of the “average” obstacle

canthenbewrittenas

ΔG =ΔG



1 −



with ΔG

=(w/2)F

=(3/8

√

2) w

APB

, F

=(w/2)γ

APB

for edge dis-

locations, and F

=(1/

√

2)wγ

APB

for screws. w is the edge length of the

octahedral particles (equal to the maximum x diﬀerence of the central cutting

plane for screw dislocations). Applying the Friedel relation for a random

arrangement of strong, wide-spaced obstacles (4.53) and setting the numerical

constants k

=1yields

ΔG =ΔG



1 −



∗



2/3



and with (4.5) and (4.8)





−2







1 −



. (7.8)

Using (4.56) and (4.50), the parameters are

ΔG

=(w/2)bl

−1/2

and T

ΔG

k ln( ˙γ

/ ˙γ)

. (7.9)

In Fig. 7.21, the activation volume is plotted according to (7.8). Here, the

factor of 3/2 in (4.55) resulting from Friedel statistics is considered, which

has not been regarded in the ﬁgures before. The full line is a linear regression

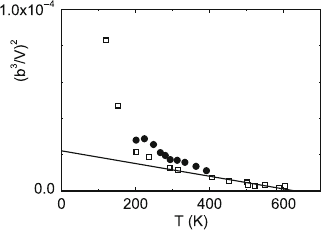
248 7 Ceramic Single Crystals

Fig. 7.21. Temperature dependence of the activation volume in MgO according

to (7.8). Data from macroscopic deformation tests [414] (open squares)andfrom

measurements of the velocity of individual edge dislocations [413] (solid circles).

Straight line: extrapolation of the data from macroscopic measurements at and above

room temperature

of the data at and above room temperature. The parameters are V

≈ 320 b

and T

≈ 635 K. In the ﬁgure, the data points for temperatures below room

temperature deviate strongly from the extrapolated course towards smaller

activation volumes, which should be due to the transition to the action of

the Peierls mechanism. With the value of f

≈ 0.8andl

= 320 b quoted

in Sect. 7.2.2, from (7.9) it follows that w amounts to a few b. On the other

hand, from the concentration of impurities, a higher value of w of about 12 b

was estimated. The “true” activation volume at room temperature V =Δdlb

from Fig. 7.17 takes a value of 300 b

if the factor of 3/2 from Friedel statistics

is considered, leading to an activation distance of Δd ≈ 1 b. All estimations

show that the particles are quite small but that the activation distance is

smaller than the width of the particles.

The total activation energy is the sum of the energy at the given eﬀective

stress plus the work term ΔF =ΔG+Vτ

∗

≈ ΔG

(4.3). Considering the yield

stress of τ ≈ 40 MPa at room temperature, the estimate of the internal stress

of τ

≈ 23 MPa in Sect. 7.2.1, and the measurements from dislocation curva-

tures in Fig. 5.28 corrected for radiation hardening, a reasonable value of the

eﬀective stress is τ

∗

≈ 22 MPa. Together with the relevant data ΔG(300 K) =

0.65 eV and V = 300 b

, it follows that ΔG

≈ 1.7 eV. This characterizes the

obstacles as strong ones, which are mainly surmounted by the applied (eﬀec-

tive) stress aided by thermal activation. With an obstacle width of w =10b,

this corresponds to a very reasonable APB energy of γ

APB

≈ 125 mJ m

−2

ΔG

is in rough agreement with the value calculated from the limiting tem-

perature T

together with k ln( ˙γ

/ ˙γ)=ΔG/T =2.17 × 10

−3

eV K

−1

from

the measured activation energies, yielding ΔG

≈ 1.4eV.

The strength τ

of the obstacle array can roughly be estimated from the

eﬀective stress τ

∗

≈ 22 MPa and the statement that τ



/τ



≈ 0.3 obtained

from the kinematic dislocation behavior (Sect. 7.2.3). According to this, the

7.2 Magnesium Oxide 249

obstacle strength may be of the order of magnitude of τ

≈ 3 τ

∗

≈ 66 MPa.

This is a high strength suggesting that the precipitation hardening mechanism

acts also at temperatures below room temperature. Thus, there is probably a

very wide range of the simultaneous action of both the Peierls mechanism and

localized obstacles. There is some disagreement between the obstacle strength

data from the macroscopic measurements and from the in situ experiments.

The data of the latter are considerably higher. This may only partly be due

to the radiation hardening observed during the in situ experiments.

In [218, 416], the dislocations were observed to move in pairs owing to

coupling by the APBs. In Sect. 8.1.3, this mechanism will be described for

alloys containing precipitates of intermetallic phases. But in the present MgO

crystals with small precipitates it does not act.

At temperatures between about 800 and 1,600 K, the yield stress remains

constant at τ

= 20 MPa. It can be explained by long-range dislocation inter-

actions. In Sect. 7.2.1, the internal stress component was estimated to amount

to τ

= 23 MPa, well agreeing with the measured yield stress. Above about

1,600 K, the yield stress may drop to lower values owing to the onset of

diﬀusion-controlled recovery. This process will be described in the section

about zirconia.

7.2.6 Dislocations in the Plastic Zone of a Crack

In a perfectly elastic solid, fracture occurs when the stress at the crack tip

reaches the theoretical cohesive stress [417, 418]. By analogy with the theo-

retical shear stress in Sect. 1.1, the latter is estimated to σ

≈ E/10, with E

being Young’s modulus. The ﬂow stress of most of the crystalline materials,

however, is essentially lower than this value so that plastic ﬂow is expected

to occur in the region of the highest stress concentration ahead of the crack.

This localized plastic ﬂow increases the resistance of the material to unstable

fracture [419, 420] and the crack propagation is essentially determined by the

size, the structure, and the internal stress distribution of the plastic zone.

During one straining experiment inside an HVEM on an MgO single crys-

tal, the stable growth of a crack on a cube face had been observed in situ

[408]. In the stress ﬁeld of the crack, a plastic zone developed with increasing

size and dislocation density. An intermediate state is presented in Fig. 7.22.

In front of the crack, the plastic zone is elongated with the dislocation density

decreasing continuously with increasing distance from the crack tip.

Under the tensile load in the in situ stage along the [010] axis, the crack

with its tip along [001] extended on a (010) plane. The tensile stress σ

of the

stress ﬁeld of the crack activated the (011)[01

1] and (01

1)[011] slip systems.

The respective dislocations bowed out under the stress. By measuring the

curvature of the bowed segments using (7.3) of Sect. 7.2.2, the dislocations

may serve as a probe to determine the spatial distribution of the stress around

the crack. As a measure of the stresses, the quantity S (ln (l/r

)+C)canbe

taken. The curvatures and segment lengths l were measured on the individual

250 7 Ceramic Single Crystals

1 µm

Fig. 7.22. Plastic zone on a crack in an MgO single crystal during in situ straining

in an HVEM. TD tensile direction. From the work in [408]

Fig. 7.23. Angle distribution of the stress parameter S (ln (l/r

)+C) in the plastic

zone of a crack in an MgO single crystal during in situ straining inside an HVEM.

Parameter: radius r =0.5 μm(solid squares), 1.5 μm(solid diamonds), 2.5 μm(solid

circles), 3.5 μm(solid triangles), 4.5 μm(open squares), 5.5 μm(open diamonds),

6.5 μm(open circles). Data from [408]

segments. The angular distribution of the stresses is plotted in Fig. 7.23 with

the distance from the crack as a parameter. The xy plane around the crack

tip is sectioned into zones of polar coordinates, 1 μm along the radius and

◦

wide. The x axis points into the crack. The values were calculated using

the theoretical constant of C = −1.61 in (7.3) or (5.18). The ﬁgure shows

only a weak maximum at ±150

◦

in front of the crack and a slight decrease

with increasing distance from the crack. The stress quantity far from the crack

7.2 Magnesium Oxide 251

amounts to about S (ln (l/r

)+C)=60μm

−1

. Thus, everywhere the eﬀective

stress within the plastic zone of the crack roughly equals the ﬂow stress of the

material.

This result can be compared with the predictions of the elastic theory of

fracture. Fracture can take place in a brittle way when the solid undergoes

only elastic deformations so that the energy necessary to extend the crack

is solely given by the energy of the additional surfaces to be created. Then,

the stress ﬁeld of the crack can be modeled by a pile-up of dislocations with

Burgers vectors perpendicular to the crack plane analogous to the shear pile-

up in Sect. 5.2.1. Instead of (5.13), the internal stress ﬁeld of the crack is then

given by

(r, φ)=f(φ)



σ, (7.10)

where the length of the pile-up is now called the crack length c and f (φ)

is again a function of φ. Thus, the crack acts as a stress concentrator with

the stresses decreasing only slowly with the distance as 1/

√

r. The critical

fracture stress σ

necessary to extend the crack can be estimated by assuming

that σ

approaches the theoretical tensile strength σ

of an ideal crystal at the

smallest possible distance in the crystal r = a,wherea is the lattice constant.

As mentioned earlier, the latter is estimated as σ

≈ E/10. For the fracture

stress there follows

≈



100c

The quantity Ea/20 can be replaced by an estimate of the surface energy γ

so that

≈



Eγ

Apart from the numerical constant (1/5 instead of 2/π), this is the Griﬃth

relation for the fracture stress of an elastic solid [417]. The latter is no mate-

rial parameter as it depends on the crack length c. The respective material

parameter is called the critical stress intensity factor deﬁned as

= σ

√

πc=



2γ

The quantity K

/E = G

=2γ

is called the crack extension force or

energy release rate. If the work necessary to create the plastic zone around

the crack is included in G

, it can be considered a fracture parameter also for

elastic/plastic fracture.

For σ<σ

and with (7.10), the stress intensity factor K = σ

√

πcdescribes

the (elastic) stress ﬁeld around the crack. This equation may then read

(r, φ)=f(φ)

√

2πr

. (7.11)

For a crack in an isotropic medium and for the tensile stress σ

, the function

f(φ) becomes (e.g., [421])