Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

262 7 Ceramic Single Crystals

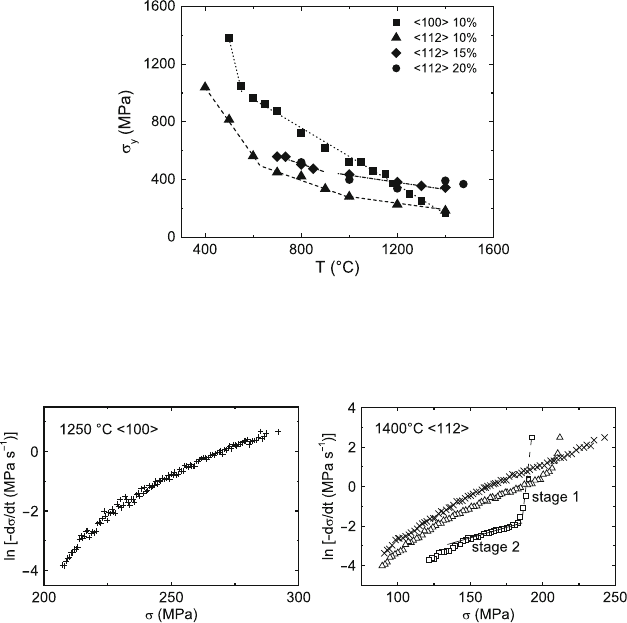
Fig. 7.33. Yield stresses σ

vs. temperature T .ZrO

–10 mol% Y

, 112 ori-

entation, ˙ε =10

−6

−1

(triangles); 100 orientation, ˙ε =10

−5

−1

(squares);

ZrO

–15 mol % Y

, 112 orientation (diamonds); ZrO

–20 mol% Y

, 112

orientation (circles). Data from [435]

(a)

(b)

Fig. 7.34. Stress relaxation curves in ZrO

–10 mol% Y

. Deformation along 100

at 1,250

◦

Cand ˙ε =10

−5

−1

(a) and along 112 at 1,400

◦

Cand ˙ε =10

−4

−1

(b).

ε =0.03% (squares), 0.32% (triangles), 2.17% (crosses). Data from [434, 435]

with decreasing stress. However, in ZrO

the curves may also have a diﬀerent

shape being bent in opposite direction. Here, such curves are designated to

have an inverse curvature. Frequently, the curves can also be described by

two stages, a very steep stage 1 at the beginning at high stress followed by

the normal behavior (stage 2) with a much lower slope and usual bending

as demonstrated in Fig. 7.34b. Two diﬀerent processes may cause the inverse

curvature. One of them is strain ageing discussed in Sect. 4.11 for range A of

Fig. 4.39, and the other one is the action of recovery. The latter takes place

in the curves of Fig. 7.34b and will be described in more detail in Sect. 7.3.5.

With increasing plastic strain, stage 2 is shifted upwards to higher strain rates

so that stage 1 disappears. It disappears also at lower starting strain rates.

The slopes at the beginning of the relaxation curves characterize the strain

rate sensitivity corresponding to the strain rate during steady deformation just

before the relaxation tests. The results are summarized on a logarithmic scale

7.3 Zirconia Single Crystals 263

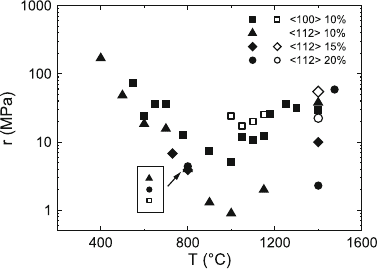
Fig. 7.35. Logarithm of the strain rate sensitivity r of the ﬂow stress as a function

of temperature T . Symbols from SR tests as in Fig. 7.33. Ful l symbols: strain rate

sensitivity at the beginning of the SR test. Open symbols: strain rate sensitivity

during stage 2 of the relaxation curves. Data from [435]

in Fig. 7.35. As r depends on the strain, the individual data are extrapolated

to a plastic strain of 0.5%. In temperature ranges where the relaxation curves

exhibit the two stages, the higher strain rate sensitivities corresponding to

the ﬂat stage 2 of the relaxation curves, that is, to strain rates considerably

lower than the rate before the relaxation test, are plotted as open symbols.

The strain rate sensitivity starts with high values at low temperatures, goes

through a minimum near 1,000

◦

C, and increases again at higher temperatures.

The data measured along 100 approach those taken along 112 at low and

high temperatures. Between about 800 and 1,200

◦

C, they are distinctly higher

by a factor of about 5. In the soft 112 orientation, r is very low at 1,000

◦

that is, only about 1 MPa. In the instability ranges of the materials with higher

yttria concentrations, strain rate sensitivities cannot be determined.

The activation energies calculated from the slopes of the yield stress vs.

temperature plots or from temperature change tests combined with strain rate

sensitivity data show reasonable values around 3 eV at low temperatures and

between 5 and 10 eV at high ones. In the intermediate range around 1,000

◦

they take very high values, which are not compatible with thermal activation.

This results from the low values of the strain rate sensitivity.

7.3.5 Deformation Mechanisms

In the diﬀerent temperature ranges, the plastic deformation of cubic ZrO

single crystals is controlled by a number of mechanisms summarized below.

The Athermal Stress Component

Long-range interactions between the dislocations cause an athermal compo-

nent τ

of the ﬂow stress. One contribution to this component is the stress

264 7 Ceramic Single Crystals

arising from the mutual elastic interaction between parallel dislocations, that

is, the Taylor hardening treated in Sect. 5.2.1. Using anisotropic elasticity, the

stress contribution τ

from parallel dislocations can be written as [432]

= αKbF



1/2

/(2π), (7.13)

where α is a numerical constant of about 8,  is the dislocation density, F

a dimensionless maximum interaction force, and K is the energy factor of the

respective dislocations. K was introduced in (3.40). It can be calculated by

anisotropic elasticity theory. In the respective formulae, it replaces the shear

modulus. As, except at high temperatures, the dislocations have mostly screw

character, K and F

were selected for screw dislocations. For 700

◦

C, they

amount to K

=80.4GPa andF

=0.30 for {100} planes (112 orientation

of compression axis) and F

=0.66 for {111} planes (100 orientation).

Using the dislocation densities for ZrO

–10 mol% Y

for the 112 and 100

compression directions mentioned in Sect. 7.3.2, the dependence of τ

on the

temperature is shown in Fig. 7.36. The values are slightly higher for the 100

orientation, owing to the higher F

value. They are compared with the total

(shear) ﬂow stress τ

calculated from σ

with the orientation factors of the

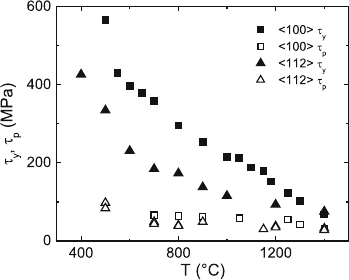
respective slip systems. In the athermal range around 1,000

◦

Cofthe112

specimens, τ

amounts to about 40 MPa. In situ straining experiments in an

HVEM (Sect. 7.3.2) showed that the dislocations move very jerkily, bowing out

between large jogs. At 1,150

◦

C, an upper limit of about 75 MPa was estimated

of the back stress τ

resulting from the bowing, which also contributes to the

athermal stress component τ

.Thus,τ

= τ

+ τ

≤ (40 + 75) MPa, which

just equals the macroscopic ﬂow stress. The athermal nature of the ﬂow stress

of ZrO

–10 mol% Y

around 1,000

◦

Calong112 is in agreement with the

Fig. 7.36. Critical resolved shear stress τ

(full symbols) and athermal ﬂow

stress component τ

from long-range interaction of parallel dislocations (open sym-

bols)ofZrO

–10 mol% Y

as a function of temperature. 112 compression axis

(triangles), 100 axis (squares). Data from [435]

7.3 Zirconia Single Crystals 265

low strain rate sensitivity (Fig. 7.35) (or the corresponding large activation

volume) and the very high experimental activation energy.

At deformation along 100, in situ straining experiments show dislocations

moving continuously on { 110} planes also bowing out to similar curvatures as

during deformation along 112. It may therefore be concluded that the back

stress τ

and accordingly also the total athermal stress component τ

assume

values similar to those along 112. In this case, however, the (shear) ﬂow

stress at 1,000

◦

C is about 200 MPa. Thus, the athermal component amounts

to only about 60% of the ﬂow stress. Along the 100 orientation, thermally

activated processes inﬂuence the ﬂow stress as it is documented by the higher

strain rate sensitivity (Fig. 7.35) and the high temperature sensitivity of the

ﬂow stress.

It may be concluded that the athermal processes yield an important com-

ponent τ

to the ﬂow stress, in particular around 1,000

◦

C. As it increases

only slightly with decreasing temperature, it becomes less important at lower

temperatures where the total ﬂow stress increases strongly.

Elastic Interactions Between Dislocations and Point Defects

Originally, the dependence of the ﬂow stress of cubic zirconia on the stabi-

lizer content at 1,400

◦

C was interpreted by solution hardening, that is, by the

elastic interaction between the dislocations and the yttrium ions, their charge

compensating oxygen vacancies or agglomerates of them (e.g., [439]). There

is a remarkable diﬀerence in the ionic radii of the yttrium and zirconium

ions, which may lead to solution hardening owing to the size misﬁt. Esti-

mates of this contribution to the ﬂow stress applying Mott–Labusch statistics

(Sect. 4.5.2) are given in [435]. As shown there, the size misﬁt interaction may

considerably contribute to the ﬂow stress of ZrO

–10mol % Y

over a wide

range of temperatures and therefore also to the materials with higher yttria

concentrations. Also the order of magnitude of the predicted activation vol-

ume ﬁts the range of experimental values. However, this model does not agree

with the functional dependencies. The experimental activation volume or the

strain rate sensitivity depend on the temperature far more strongly than pre-

dicted theoretically. Besides, the strain rate sensitivity should be proportional

to the square root of the yttrium concentration instead of being independent

of it. In particular, the obstacle distances in the range of 0.1 μmobservedby

transmission electron microscopy in Sect. 7.3.2 disagree with the very short

distances of only a few b between the individual yttrium ions. It may therefore

be concluded that direct solution hardening by the solved yttrium ions only

weakly contributes to the ﬂow stress.

Agglomerates of yttrium ions and oxygen vacancies form electric and elas-

tic dipoles, which were proved by mechanical loss spectroscopy (e.g., [440]).

As the mobility of the oxygen vacancy near the yttrium ion is very high, the

relaxation maxima are below 400

◦

C, that is, these defects do not act as ﬁxed

266 7 Ceramic Single Crystals

obstacles within the range of the present experiments. The respective reori-

entation processes might lead to the induced Snoek eﬀect in the temperature

range of the relaxation maxima, that is, also below the present temperature

range. At higher temperatures, the agglomerates dissociate (e.g., [440]).

Precipitation Hardening

Plastic deformation in the temperature range between about 500 and 800

◦

seems to be controlled essentially by precipitation hardening. The ﬂow stress

exhibits a moderate temperature sensitivity (Fig. 7.33). The strain rate sen-

sitivity (Fig. 7.35) corresponds to activation volumes of some tens to some

hundreds of b

. The Gibbs free energy takes reasonable values mostly below

6 eV but its increase with temperature is too strong for a single thermally

activated process so that another thermally activated process should be super-

imposed, probably the Peierls mechanism at low temperatures. The occurrence

of precipitation hardening is supported by the bowed-out shape of the dislo-

cations in the respective temperature range (Figs. 7.25, 7.26, and 7.31). The

comparison between the activation volume V = lbΔd of the order of magni-

tude of 100 b

(at about 800

◦

C), determined macroscopically, and the obstacle

distance of l ≈ 250 b reveals that the activation distance Δd is a fraction of b.

As the precipitates are certainly much larger, this indicates that the eﬀective

forces on the obstacles almost reach the obstacle strength so that only the tips

of the obstacles are overcome by thermal activation. As shown in Fig. 7.35, the

strain rate sensitivity and thus also the activation volume are not inﬂuenced

by the yttria concentration. Thus, the precipitates should not be connected

with the yttria stabilizer. Unfortunately, only a hypothesis can be presented

of the nature of the precipitates. According to [441], high concentrations of

nitrogen are solved in zirconia crystals owing to their growth in air. At high

temperatures, they precipitate to form ZrN particles. As the ZrN precipitates

occur at all yttria concentrations studied in [441] and as the crystal material

was supplied by the same company as the present one, it is believed that

small particles containing nitrogen cause the precipitation hardening in the

temperature range between 500 and 800

◦

In [213,324], the temperature dependence of the yield stress and the strain

rate sensitivity of the 10 mol% material in the precipitation hardening range

are interpreted by a phenomenological obstacle potential suggested in [9]

ΔG(τ

∗

)=ΔG



1 −



∗



1/2



3/2

with an activation energy at zero stress of ΔG

≈ 4.2 eV and of an athermal

stress of the obstacle array of τ

≈ 1, 760 MPa. The results for the ﬂow stress

are plotted in Fig. 7.37 and for the strain rate sensitivity already in Fig. 4.23.

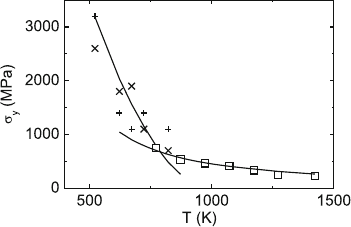
Figure 7.37 contains also low-temperature data from [214] obtained under

conﬁning hydrostatic pressure to avoid brittle failure.

7.3 Zirconia Single Crystals 267

Fig. 7.37. Temperature dependence of the yield stress of cubic ZrO

deformed

along 112. Experimental data at ambient atmosphere and ˙ε =10

−6

−1

of ZrO

–

10 mol% Y

(open squares); at conﬁning hydrostatic pressure and ˙ε =2×10

−4

−1

[214], ZrO

–12.6 mol% Y

(upright crosses), ZrO

–10 mol% Y

(tilted crosses).

Data from [213]

The diﬀerence in the ﬂow stresses of ZrO

–10 mol% Y

deformed along

100 in comparison to 112 at intermediate temperatures should be related

to the dominating thermally activated mechanism, that is, to precipitation

hardening, as the strain rate sensitivity is much higher along 100 than along

112. The obstacle distances, however, are practically equal in both directions

in agreement with the fact that the dislocations interact with the same obsta-

cles in both orientations. An equal obstacle distance l but a higher strain rate

sensitivity along 100 (Fig. 7.35) result in a smaller value of the activation dis-

tance Δd. The details of this mechanism are not yet understood well. While for

the reference specimens of ZrO

–10 mol% Y

deformed along 112, precipi-

tation hardening ceases in the athermal range around 1,000

◦

C, it still seems to

operate at these temperatures for deformation along 100. The contribution

of precipitation hardening seems to be independent of the stabilizer concen-

tration. Thus, it does not explain the higher ﬂow stress of the materials with

higher yttria concentrations.

The Peierls Mechanism

Below about 500

◦

C, the ﬂow stress of the material with 10 mol% yttria

deformed along 112 increases strongly, as demonstrated in Fig. 7.37. This

behavior is related to a steep rise of the strain rate sensitivity shown before in

Fig. 4.23. In [212, 213], it is interpreted by the transition to the action of the

Peierls mechanism. The large strain rate sensitivity below 500

◦

C corresponds

to activation volumes below about 10 b

,whicharewellconsistentwiththe

Peierls mechanism. Specimens deformed along 100 also show a steep increase

of the ﬂow stress at 500

◦

C, and at low temperatures the activation volumes

approach the values in the soft orientation. Thus, the Peierls mechanism is

supposed to be also active on the non-cube slip planes at low temperatures.

268 7 Ceramic Single Crystals

However, the Peierls mechanism does not seem to be responsible for the dif-

ference of the ﬂow stresses for slip on cube or non-cube planes (for the two

loading directions) over a wide range of temperatures, as above about 800

◦

the activation volumes are too large for this mechanism. The specimens with

yttria concentrations higher than 10 mol% broke before the range of the Peierls

mechanism was reached.

The theory of the transition from the Peierls mechanism to the action of

localized obstacles was outlined in Sect. 4.6. It particularly explains the very

strong increase in the strain rate sensitivity in the transition region (Fig. 4.23).

Formation of Solute Atmospheres Around Dislocations

While along 112 the ZrO

–10 mol% Y

crystals show an athermal defor-

mation behavior around 1000

◦

C with very low strain rate sensitivities, spec-

imens with 15 and 20 mol% yttria exhibit plastic instabilities discussed in

Sect. 5.3. This is usually interpreted by the Portevin–LeChatelier (PLC) eﬀect

[346, 347] or dynamic strain ageing, leading to a locking of the dislocations

and to an additional contribution to the ﬂow stress (Sect. 4.11).

There are similarities between the load drops of serrations shown in

Fig. 5.31 and stress relaxation tests performed in stable ranges near the insta-

bilities. In both cases, deformation takes place at decreasing load with the

only diﬀerence that during relaxation tests the deformation is driven only by

the relaxing elastic deformation of the load train, while at serrated ﬂow the

driving rate of the machine is superimposed. In the instability range, stress

relaxation curves frequently consist of sudden load drops followed by periods

of constant load. At suﬃcient time resolution, these load drops turn out to

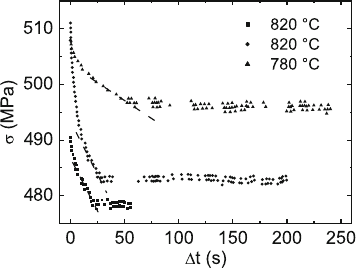
be sections of relaxation curves as shown in Fig. 7.38 taken at temperatures

around 800

◦

C. When the relaxation rates (slopes of the curves) have reached

certain temperature-dependent minimum values marked by the straight lines,

the stress remains constant, that is, the relaxation rates turn to zero. In other

Fig. 7.38. Stress vs. time plots of relaxation tests on ZrO

–15 mol% Y

−5

−1

and 780 and 820

◦

C. Data from [344]

7.3 Zirconia Single Crystals 269

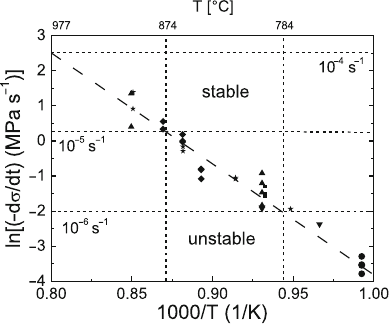
Fig. 7.39. Arrhenius plot of the minimum relaxation rates measured during stress

relaxation tests. Horizontal dashed lines mark plastic strain rates corresponding to

the relaxation rates. Data from [344]

words, below the minimum relaxation rates the dislocations will be totally

blocked so that no plastic deformation is possible at lower rates. In the case of

serrations, dislocation motion becomes blocked, too, if the strain rate reaches

its minimum value, and elastic loading starts again. Figure 7.39 veriﬁes that

the minimum strain rates obey an Arrhenius relation with an experimen-

tal activation energy of Q =2.7 eV. As the minimum deformation rates are

the limiting rates below which the deformation is blocked, the Arrhenius line

should describe the lower border of the instability range. It actually separates

the ranges of stable and unstable deformation.

It is argued in [344] that the plastic instabilities and the yttria concen-

tration dependence of the ﬂow stress between about 800 and 1,200

◦

Care

caused by short-range diﬀusion of unassociated yttrium ions according to

the theories of the Cottrell eﬀect and the instabilities outlined in Sects. 4.11

and 5.3. Equations (3.32), (4.99), and (4.100) can be used to estimate the

properties of the maximum of the strain ageing curve in Fig. 4.39. Numerical

values of the ionic radii of Y

and Zr

are 0.102 and 0.084 nm, yielding

− V

)/b

=0.0397, where V

and V

are the ionic volumes of the solute

and matrix ions. A characteristic dislocation density is  =10

−2

.Itmay

be assumed that the maximum of the curve in Fig. 4.39 is identical with the

upper instability border at T

≈ 1, 400

◦

C. Then, (4.99) and (4.100) can be

used to estimate the necessary diﬀusion coeﬃcient for the deformation at

˙γ

=10

−5

−1

. It turns out that D ≈ 6×10

−19

−1

. This value can be com-

pared with diﬀusion data, considering that the diﬀusion coeﬃcient of yttrium

should be similar to that of zirconium (e.g., [442]). The value estimated of

D ﬁts well that extrapolated between the cation diﬀusion data from the loop

shrinkage study in [443] for ZrO

–10 mol% Y

at lower temperatures and

the interdiﬀusion data [442] at higher ones. Although this does not prove the

270 7 Ceramic Single Crystals

model, it shows that the diﬀusion of yttrium ions should be fast enough to

cause dynamic strain ageing.

Equation (4.100) gives a rough estimate of the contribution of dynamic

strain ageing to the ﬂow stress. Using the same data as above and considering

that part of the yttrium ions are associated it follows that τ

max

≈ 3GPa.

This is one order of magnitude higher than the total ﬂow stress. Thus, defects

of much weaker interaction are suﬃcient to essentially contribute to the ﬂow

stress by dynamic strain ageing. The occurrence of dynamic strain ageing

may give rise to a ﬂow stress anomaly owing to the maximum in the curve of

Fig. 4.39. In zirconia with high yttrium concentrations, the increasing contri-

bution of dynamic strain ageing to the ﬂow stress at temperatures increasing

up to 1,400

◦

C may compensate the decreasing contributions of other mech-

anisms yielding an almost constant ﬂow stress. At temperatures above the

upper border of the instability range, fast cation diﬀusion results in a decrease

of the ﬂow stress by both the decreasing action of dynamic strain ageing and

the occurrence of dynamic recovery.

The low-temperature border of the instability range is connected with

the sharp transition between plastic deformation at a minimum rate and the

complete blocking by full ageing of the dislocations during stress relaxation

tests. At this transition, the velocity of diﬀusing solutes becomes equal to

the velocity of moving dislocations. Thus, the temperature dependence of the

minimum rates demonstrated in Fig. 7.39 is directly connected with the tem-

perature dependence of the underlying diﬀusion process. There are no cation

or solute diﬀusion data available for temperatures as low as 800

◦

C. The low-

est temperature of 1,100

◦

C was reached in the loop shrinkage experiments of

[443], yielding an activation energy of 5.3 eV. The substantially lower acti-

vation energy of 2.7 eV observed in Fig. 7.39 for the dislocation locking may

therefore correspond to short-range diﬀusion in the dislocation cores. Thus,

the character of the diﬀusion processes may change from short-range diﬀusion

in the dislocation cores at the low-temperature border of the Cottrell eﬀect

region to bulk diﬀusion at the high-temperature one.

Recovery Controlled Deformation at High Temperatures

The deformation of c-ZrO

at temperatures around 1,400

◦

C was discussed in

detail in terms of recovery-controlled glide in [434] after the original sugges-

tion in [438]. Similar views were also expressed, for example, in [436]. The

importance of recovery is documented by the presence of a dislocation net-

work (Fig. 7.30), which may form during multiple slip by the Burgers vector

reaction

1/2[1

10] + 1/2[01

1] = 1/2[10

and by a decrease of the dislocation density and the corresponding athermal

component of the ﬂow stress (Fig. 7.36).

Although in the recovery range the ﬂow stress strongly depends on the

temperature, it may consist mainly of two athermal contributions. One is

7.3 Zirconia Single Crystals 271

the long-range interaction between parallel dislocations which, after Fig. 7.36,

amounts to τ

≈ 30 MPa for ZrO

–10 mol% Y

deformed along 122.The

other is the back stress τ

, which the dislocation segments have to overcome

to bow out between the nodes of the network, that is, the Frank–Read stress

(3.47). With the experimental segment lengths L between 1 and 2.5 μmand

the suitable shear modulus, it follows that τ

=13... 28 MPa. Thus, the

athermal component of the ﬂow stress of about 50 MPa amounts to about

two-thirds of the total ﬂow stress. This is a lower limit as the measured dislo-

cation densities may be underestimated because of the recovery, even for the

specimens cooled under load.

The recovery model, in [434] proposed for cubic zirconia, follows a theoret-

ical suggestion by Kocks [444,445] and may particularly explain the two-stage

dynamic behavior of the material during stress relaxation tests demonstrated

in Fig. 7.34. It is a constitutive model considering both a dynamic law, which

controls the mobility of dislocations, and an evolution law of the development

of the dislocation structure. The dynamic law can be represented by the power

law (4.103) in the form of

˙γ =˙γ

(τ/τ

)

. (7.14)

Here, τ

is a threshold stress, which is related to the long-range stress com-

ponent τ

= τ

+ τ

of the order of magnitude of 50–75 MPa, ˙γ

is a constant,

and m is the dynamic stress exponent (4.10). It need not be identical with

the experimental stress exponent m



deﬁned by (4.12). During straining, the

microstructure changes. This is described by an evolution law

dτ

/dγ = Θ



1 − Rτ

˙γ

−1/n



, (7.15)

where Θ

is the initial work-hardening coeﬃcient, and n is the strain-softening

exponent. The last term in the parentheses considers dynamic recovery via

glide and climb, where R includes the diﬀusion coeﬃcient. As observed in

the loop shrinkage study of [443], the diﬀusion coeﬃcient strongly depends

on the yttria concentration, which explains the dependence of the ﬂow stress

on the latter. Under steady state conditions as in creep, τ

is constant so that

˙γ

=(Rτ

)

= R





, (7.16)

with 1/n



=1/n +1/m. This is the well known creep law (5.20). In the

present experiments at a constant strain rate, the work-hardening is low after

the yield point so that (7.16) should also account for the steady state ﬂow

stress. Equations (7.14) and (7.15) describe also the transient phenomena as

occurring in the stress relaxation experiments. For these experiments, (7.14)

and (7.15) can be solved under the (well fulﬁlled) assumption that the actual

stress τ is nearly equal to the threshold stress τ

, yielding



=dln˙γ/dlnτ =dln(−˙τ )/dlnτ

= m −

(m −n) A (τ/τ

)

(1 − A)(τ/τ

)

m/n

+ A (τ/τ

)

, (7.17)