Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

282 8 Metallic Alloys

shorter ageing times are under-aged, while those with longer ageing times are

over-aged.

In several aluminium alloys, the particle microstructures are very well stud-

ied so that the yield stresses of the materials can be modeled by the theories

discussed in Sects. 4.5 and 4.7. However, by applying conventional methods,

one often cannot decide whether the precipitates considered are the relevant

obstacles to dislocation glide controlling the ﬂow stress or not. In situ strain-

ing experiments in an HVEM, which reveal the morphology and kinematics

of the dislocations overcoming the particles, may help answer these questions.

The relevant obstacles need not have the density and strength analyzed by

other methods. The quantitative data that can be obtained from the in situ

experiments are used to check the predictions of the models.

8.1.1 Al–Zn–Mg

The alloy Al-4.54 wt% Zn-1.18 wt% Mg is a material for technical application.

For the described experiments [226], specimens were heat treated to grow

particles of the η



phase which are large enough to be imaged in the HVEM

as small dark dots shown before in Fig. 4.30. These semicoherent particles

are supposed to be visible mainly due to structure factor contrast. Under the

imaging condition with higher-order reﬂections, almost all particles should be

visible, and the size of the contrast dots should correspond to the extensions

of the particles. The particles have an average diameter of D =10.5nm and

an average volume of V =1.06 × 10

−24

. They ﬁll a fraction of f =0.33%

of the volume. Considering the disc shape of the particles, this is by a factor

of more than 10 less than the atomic concentration of the Zn and Mg being

added. As a measure of the obstacle density, the square lattice distance deﬁned

in (4.48) can be calculated by



π/(6f ) D. (8.1)

From the above data, it follows that l

= 170 nm.

The in situ straining experiments (Fig. 4.30) show dislocations pinned at

localized obstacles and strongly bowing out between them. These conﬁgura-

tions correspond to the so-called stress determining conﬁgurations mentioned

in the theory in Sect. 4.5. For measuring the obstacle distances, all cusps in

the dislocation lines are considered. The distances obey the typical asymmet-

ric shape of the theoretical distribution of Fig. 7.10 with an average value

of l = 62 nm. Eﬀective stresses were determined from the curvature of the

bowed-out dislocation segments using the loop ﬁtting method described in

Sect. 7.2.2, yielding the reciprocal major half-axis S = e

−1

=16μm

−1

of the

ﬁtting ellipses as well as the eﬀective stress τ

∗

according to (7.3). In con-

trast to the evaluation for MgO, where curvature data were determined from

all segments, only clearly imaged segments were selected in the aluminium

alloys, because of the reduced quality of the dislocation images due to the

8.1 Precipitation Hardened Aluminium Alloys 283

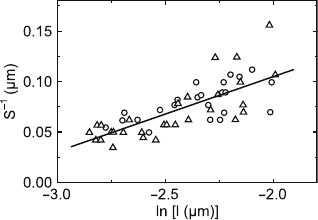
Fig. 8.1. Dependence of the dislocation bowing S on the logarithm of the segment

length l in Al–Zn–Mg. Data from [115]

superposition of the contrasts of the precipitates. This selection of segments

will certainly prefer strongly bowed segments, leading to higher values of τ

∗

The dependence of the dislocation curvature on the logarithm of the segment

length, predicted by the theory in Sect. 3.2.7, was proved also for this alloy,

as illustrated in Fig. 8.1. The constant in (3.45) amounts to C = −4.6, in

agreement with the results for MgO. Nevertheless, the theoretical constant

C = −1.61 was used for the evaluations. These methodical remarks hold also

for the other aluminium alloys discussed later.

With (7.6), it follows from l and S that l

=60nm≈ l. Accordingly, the

square lattice distance measured directly at the pinned dislocations l

is only

one third of the value l

following from the concentration and size of the pre-

cipitates visible in the electron microscope. This means that the dislocations

“feel” about ten times more obstacles than the η



particles. The latter grow

from Guinier–Preston zones, which are still present in the material. They are

strong obstacles due to their stress ﬁeld but they are not visible in the HVEM

micrographs. They were not considered important before the in situ experi-

ments were carried out. As the dislocations move very jerkily over distances

long compared to the obstacle distances, most of the dislocation conﬁgura-

tions are unstable or j ≈ 1 in Fig. 4.18. As a consequence, the normalized

stress τ



following from the dislocation curvature is only slightly lower than

the athermal strength τ



of the obstacle array. The overcoming of the obsta-

cles is then more or less of athermal nature. The obstacle data, together with

the data of the other Al alloys, are summarized in [115] and in Table 8.1. The

values of the eﬀective stress τ

∗

are partly very high owing to the theoretical

value of the constant C = −1.61 used in (3.45). It may be concluded from

the in situ experiments on the Al–Zn–Mg alloy that the concentration of the

precipitates is strongly underestimated from the size and density of particles

visible in the electron micrographs. The obstacles are quite strong and are

overcome in an athermal way.

The ﬂow stress component from precipitation hardening is certainly not

the only contribution to the ﬂow stress of the order of magnitude of σ =

200 MPa. A stress component due to Taylor hardening from long-range

284 8 Metallic Alloys

elastic interactions between dislocations is estimated via (5.11) to amount to

≈ 25 MPa at a dislocation density of 5 × 10

−2

. Further information on

the deformation processes can be inferred from the macroscopic deformation

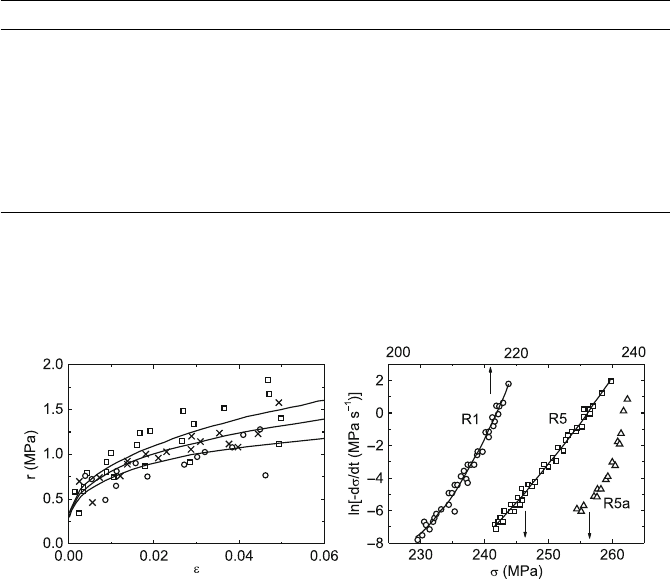
properties. Figure 8.2a presents the dependence of the strain rate sensitivity

r measured by strain rate cycling tests on the strain, with the strain rate

as a parameter. In general, the r values of about 1 MPa are very low result-

ing in high stress exponents m



= σ/r, which are characteristic of athermal

deformation. The activation volume V of about 450 b

ﬁts the segment length

of l ≈ 220 b, yielding an activation distance of Δd = V/(bl) ≈ 2 b.Ther

values show the usual increase with strain due to work hardening. The inter-

esting point is the inverse dependence on the strain rate, which also holds for

Table 8.1. Parameters characterizing the interaction between dislocations and

precipitates in Al alloys

Al–Zn–Mg Al–Ag, 6 h Al–Ag, 9 h Al–Li, leading disls.

l (nm) 62 111 117 56

S (μm

−1

) 16 11.2 14.9 17

(nm) 60 ≈110 ≈110 53

(nm), CTEM 170 ≈20 ≈20 34



0.48 0.62 0.87 0.45

∗

(MPa) with C = −1.61 59 45 60 59

estimated τ



0.5 0.65 0.9 0.5

C −4.6 −5.6

The lines are: segment length, reciprocal major half axis of ellipses ﬁtting bowed-

out dislocation segments, square lattice distance from in situ experiments, square

lattice distance from conventional transmission electron microscopy (CTEM), nor-

malized eﬀective stress, eﬀective stress, normalized athermal strength of obstacle

array, constant in (3.45)

(a)

(b)

Fig. 8.2. Strain rate sensitivity of the Al–Zn–Mg alloy. Dependence of the strain

rate sensitivity measured by strain rate cycling tests on the strain with the strain

rate as parameter (a). ˙ε =4×10

−6

−1

(squares), 4×10

−5

−1

(crosses), 4×10

−4

−1

(circles). Stress relaxation curves (b). R5a is a repeated relaxation after R5. Data

from [226]

8.1 Precipitation Hardened Aluminium Alloys 285

the ﬂow stress itself. This inverse dependence is also obvious from the course

of stress relaxation curves plotted in Fig. 8.2b, with their abnormal bending

away from the stress axis. As described in Sect. 4.11, the inverse dependence

of r on ˙ε may result from diﬀusion processes in the dislocation cores and

corresponds to range A in Fig. 4.39. These eﬀects are also manifest as strain

ageing when the deformation machine is stopped and as the strong reduction

of the relaxation rate at the repeated relaxation R5a with respect to the orig-

inal relaxation R5. As described in Sect. 2.1, diﬀerences between an original

relaxation curve starting from continuous deformation and a repeated one

started before steady deformation is reached, again document changes in the

microstructure during the ﬁrst relaxation. According to [452], a great part

of the additions remain in solution and can associate with vacancies [453] to

form mobile elastic dipoles, which may generate Snoek atmospheres around

the dislocations and contribute to the ﬂow stress. Thus, the combined use of

microscopic and macroscopic methods is necessary to gain information on the

diﬀerent processes controlling the ﬂow stress.

8.1.2 Al–Ag

Al–Ag alloys are a model system to investigate the decomposition of super-

saturated binary alloys and the inﬂuence of the resulting obstacle spectra

on the mechanical properties. Very detailed studies have been performed on

the decomposition kinetics and the inﬂuence of the size and density of the

precipitates on the yield stress of an Al-1 at% Ag alloy isothermally aged at

413 K after a suitable solution treatment [454, 455]. As a result, the mate-

rial shows a remarkable anomaly of the ageing kinetics during 10 h, where a

primary increase in the ﬂow stress is followed by a drop and a re-increase.

As the silver-rich particles have neither a marked lattice constant misﬁt nor

a modulus misﬁt, stacking fault hardening is considered the main strength-

ening mechanism [456]. The primary increase was interpreted on the basis

of the size and density of precipitates determined by high-resolution electron

microscopy [454]. However, in situ straining experiments in an HVEM [283]

showed that the basic assumption was not fulﬁlled that all precipitates visible

in the electron microscope represent the relevant obstacle spectrum.

The in situ study was aimed at observing diﬀerences in the dislocation

behavior between the under-aged state after ageing at 413 K for 6 h and the

peak-aged state after 9 h. The basic features of the dislocation structure during

in situ straining are shown in Fig. 8.3. Similar micrographs were obtained for

both ageing states. As in Al–Zn–Mg, the dislocations exhibit a curly shape,

bowing out between localized obstacles. Such micrographs allow the obstacle

distances l and l

to be determined as well as the curvature data S and



all listed in Table 8.1. Included in the table are also the square lattice

distances l

calculated from high-resolution TEM. Diﬀerent from Al–Zn–Mg,

the relevant obstacle distances along the dislocations are now about 5 times

larger than those predicted from the size and density of contrast dots in the

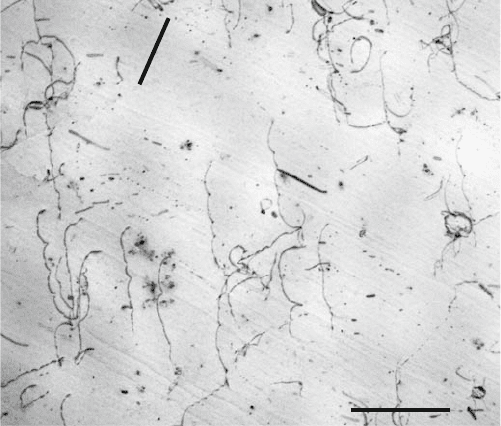
286 8 Metallic Alloys

1 µm

Fig. 8.3. Dislocation structure in an Al-1 at% Ag single crystal aged at 413 K for

9 h, taken during in situ deformation in an HVEM at room temperature. Dislocation

loops L. g = [600] parallel to tensile axis, (0

11) foil normal. From the work in [283]

high-resolution micrographs. Thus, only part of the precipitates are active as

pinning points along the dislocations. While the square lattice distances are

almost equal for the two annealing states, the normalized stress for the peak-

aged state is clearly higher than that of the under-aged state. These stresses

are all very high, indicating that the precipitates are strong obstacles.

The dynamic behavior of the dislocations is demonstrated in the following

video clip.

Video 8.1. Dislocation motion in an Al-1 at% Ag single crystal at room tem-

perature: The clip consists of four short sequences of the same specimen area,

demonstrating the pinning of dislocations by the small precipitates. The dislocation

motion is very jerky over distances far longer than those between the precipitates.

Frequently, dislocation debris and larger dislocation loops are produced very sud-

denly. The appearance and disappearance of a large loop is indicated by a green

circle to the left of the site of the event.

As discussed for Al–Zn–Mg, the jerky motion over larger distances means that



is only slightly smaller than the strength of the obstacle array τ



As mentioned earlier, stacking fault strengthening is widely accepted as the

main hardening mechanism in two-phase Al–Ag alloys [456,457]. Owing to the

diﬀerence between the stacking fault energies γ

of aluminium (200 mJ m

−2

)

and silver (20 mJ m

−2

), a dislocation that encounters a (silver-rich) precipitate

will split into two partials enclosing a stacking fault. Following [456], the

contribution to the critical resolved shear stress τ

is given by

8.1 Precipitation Hardened Aluminium Alloys 287

Δγ

, (8.2)

with the quantities deﬁned in Sect. 4.5 (F

maximum interaction force between

dislocation and precipitate, l mean distance between obstacles in the slip

plane). Δγ

is the diﬀerence between the stacking-fault energies of the pre-

cipitate and the matrix, and d is the eﬀective length of the dislocation in the

particle. The equation holds for the athermal surmounting of the obstacles,

which is in agreement with the large slip distances observed in the video clips.

The eﬀective length d of the dislocation in the particle depends on the relation

between the particle radius and the splitting widths of the dislocation in the

matrix as well as in the particle.

The result of l

≈ 5 l

shows that the dislocations are not interacting with

all particles present. It seems likely that a small number of strong obstacles

governs the hardening behavior of this alloy. This view is supported by the

fact that the curvature of the dislocation segments between the obstacles can

explain the whole ﬂow stress. It is well-known that the precipitates consist of

ε and η particles (e.g., [458]). Al-Kassab and Haasen [459] applied a ﬁeld ion

microscope-atom probe to investigate an Al-3 at% Ag alloy, isothermally aged

at 413 K for diﬀerent times. They found that, from early to intermediate stages

of decomposition, ε and η precipitates coexist with diﬀerent concentrations of

silver atoms of 31 and 57%. It may be assumed that the silver-rich η precip-

itates control the ﬂow stress. In a mixture of obstacles of diﬀerent strengths,

the mean obstacle distance is determined mainly by the concentration of the

strong obstacles (Sect. 4.5.1).

Equation (8.2) can be used to estimate the diﬀerence Δγ

between

the stacking-fault energies of the matrix and the precipitates. The follow-

ing parameters are applicable to the specimens aged for 6 h: d =2.3nm,

l = 110 nm, and τ

= 17 MPa from the macroscopic experiments [455]. This

results in Δγ

= 240 mJ m

−2

, which is even larger than the stacking fault

energy of 200 mJ m

−2

for aluminium. On the other hand, the cutting planes

of the particles are, on the average, smaller than the particle diameter consid-

ered above. Thus, the obstacles observed in the in situ experiments seem to be

stronger than the usual models of stacking-fault strengthening can explain.

Possible explanations of this discrepancy are given in [283]. Because of the

low stacking fault energy in the particles, the stacking fault width should be

greater than the particle diameter. In this case, the stacking fault ﬁlls the

whole particle and the dislocation is ﬁxed to the particle border. This results

in an additional elastic contribution to the interaction energy between particle

and dislocation [456].

8.1.3 Al–Li

Because of their light weight connected with high elastic stiﬀness and strength,

aluminium–lithium alloys are of considerable technical interest. They harden

288 8 Metallic Alloys

by precipitates of the ordered δ



phase by analogy with nickel base alloys

containing Ni

Al precipitates. The precipitates have the L1

structure. A dis-

location of the matrix with an a/2110 Burgers vector produces an antiphase

boundary (APB) in the particle. It can be removed when a second dislocation

of the same Burgers vector is passing. Thus, the second dislocation moving

exactly on the same slip plane is drawn into the particles with antiphase

boundaries. This opposes the elastic repulsion between the two dislocations.

Accordingly, it is energetically favorable if the dislocations move in pairs

leaving particles without faults on the cutting planes. The respective the-

ory [460–462] has originally been developed by Gleiter and Hornbogen and

is reviewed in [224]. Evaluations of particle distributions and macroscopic

measurements of the mechanical properties are given in [463–466].

Dislocation processes in single crystals grown from the commercial alloy

P53 from Alcan were observed in in situ straining experiments in an HVEM

[284, 467]. The single crystals contained 8.4 at% Li and were homogenized

at 843 K. Afterwards, precipitates of the δ



phase were grown by two-stage

annealing. The δ



particles were spherical, having an average diameter of

D =15.6 nm and a volume fraction of f =0.11. The alloy is then in the

under-aged state.

Figure 8.4 shows a typical dislocation structure. The dislocations move in

pairs, in accordance with other microstructural observations (e.g., [468]). The

leading dislocations of the pairs strongly bow out between pinning points. The

trailing dislocations are less strongly bowed, but also in forward direction. In

other parts of the specimens the dislocations move as single dislocations as

in Fig. 8.5. They also bow out between obstacles. In general, the dislocations

move very jerkily, usually over distances larger than a micrometer, which

indicates that the stress is close to the athermal strength of the obstacle array

(see Sect. 4.5.1, Fig. 4.18). Most dislocations show a loose arrangement, with

each dislocation or dislocation pair moving on an individual slip plane.

Quantitative data from dislocation pairs can be obtained from the micro-

graphs of dislocations under load using the model mentioned above and

outlined in Fig. 8.6. The leading dislocation 1 has to create the antiphase

boundaries inside the precipitates. It is driven by the applied stress τ and the

repulsive internal stress τ

arising from the trailing dislocation 2. Accordingly,

the following force balance holds

(τ + τ

) l

b − γ

APB

=0, (8.3)

where l

is the obstacle distance and D

the eﬀective particle diameter along

the leading dislocation, and γ

APB

is the antiphase boundary energy.

The second dislocation is pushed forward by annihilating the antiphase

boundaries in the particles and backward by the internal stress. Thus,

(τ − τ

) l

b + γ

APB

=0. (8.4)

Theobstacledistancel

and the eﬀective particle diameter D

generally diﬀer

from the respective values of the leading dislocation. According to (3.24) and

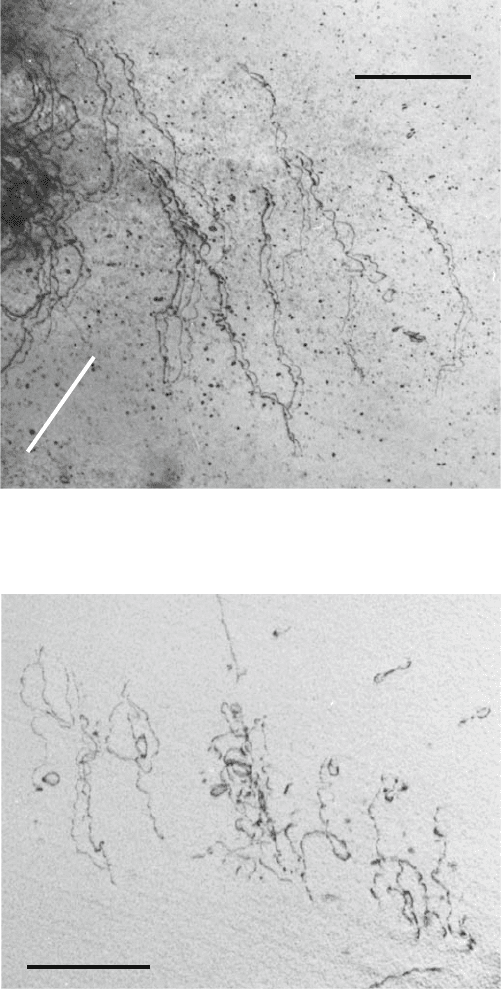
8.1 Precipitation Hardened Aluminium Alloys 289

1 µm

Fig. 8.4. Slip band of dislocation pairs in an Al-8.4 at% Li single crystal during in

situdeformationinanHVEMatroomtemperature. TD tensile direction. From the

work in [284]

1 µm

Fig. 8.5. Slip band of unpaired dislocations in an Al-8.4 at% Li single crystal during

in situ deformation in an HVEM at room temperature. From the work in [284]

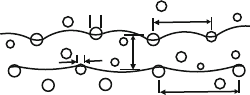
290 8 Metallic Alloys

Fig. 8.6. Outline of the model of dislocation pairs in alloys with precipitates of an

ordered structure

with y

= 0, the internal stress between the dislocations of the pairs is given

= μb/(2πx)

for screw dislocations, and by

= μb/(2π[1 − ν]x)

for edge dislocations. Strictly speaking, these formulae hold only for straight

dislocations. x is the distance between the dislocations, which can be measured

from the micrographs.

Dislocation motion in pairs was simulated in Nimonic PE16, a material

strengthened in a way similar to the present Al–Li alloy by particles that have

to be cut by forming antiphase boundaries. The precipitates are also of the

structure. The following video presents an example of the simulation by

V. Mohles performed in the group of E. Nembach at M¨unster University.

Video 8.2. Simulation of the motion of a dislocation pair in Nimonic PE16:

The video sequence presents the simulation of the motion of a pair of edge dis-

locations under conditions very similar to those in the in situ experiments on

Al-8.4 at% Li. The volume fraction of the precipitates amounts to f =0.089, the

radius of the particles is r =24b, and the normalized antiphase boundary energy

is g = γ

APB

/(bμ)=0.015. The simulation considers the obstacle resistance, the

interaction between the dislocations of the pair as well as the self-stress of the bow-

ing dislocation itself. In addition, viscous damping is included. a in the legend is

the fraction of the area swept. Details of the simulation method and some results

are given in [469]. The video shows the coupled motion of the (red) leading dis-

location and the (blue) trailing dislocation. As expected, the leading dislocation

strongly bows out while the trailing dislocation is quite smooth. The latter corre-

sponds to the model where the trailing dislocation is pushed forward by removing

the antiphase boundaries in the particles cut before by the leading dislocation. These

forward forces should be balanced by a slight backward curvature of the connected

dislocation segments in the matrix. However, this is in contrast to the experimental

observation that the trailing dislocations are bowed-out in forward direction, too.

Note that the normalized stress s =10

τ/μ, indicated in the legend, is raised by a

factor of almost two during the motion. If the critical (ﬁnal) stress had acted right

from the beginning, the dislocations would have swept most of the area very quickly.

Nevertheless, the damped motion visible also in the last part of the video does not

correspond to the underdamped jerky motion in the experiments on Al–Li.

8.1 Precipitation Hardened Aluminium Alloys 291

Table 8.2. Interaction parameters of leading dislocations in pairs and single screw

dislocations with precipitates in Al-8.4 at% Li (Data from [284])

Disl. pairs Single screws

Screws Edges

l (nm) 58.9 52.7 53.6

S (μm

−1

) 17.5 16.5 18.5

(nm) 57.5 47.5 51.5

1/x(μm

−1

) 19.1 18.3

∗

(MPa) 62.7 55.3 68.0

(MPa) 22.5 33.7

τ (MPa) 40.2 21.6

From the micrographs taken during the in situ experiments, the same

data as for the other aluminium alloys before were determined for the leading

dislocations of the pairs, separately for those of dominating screw and edge

character, as well as for unpaired screw dislocations. Details of the evaluation

are given in [284]. The results are listed in Table 8.2. In Sect. 8.1.1, the data

of Table 8.1 are averages of the values of screws and edges. The present alloy

shows also the dependence of the dislocation curvature on the logarithm of

the segment length as predicted in (3.45) and proved for MgO and Al–Zn–

Mg. The constant C is included in Table 8.1 and ﬁts the values of the other

materials.

Using (8.1), a theoretical value of the square lattice distance can again

be calculated from the average particle diameter and volume fraction cited

above, yielding l

= 34 nm, which is in relatively good agreement with the

measurements from the in situ experiments.

In the force balance (8.3), all parameters are known except the antiphase

boundary energy γ

APB

and D

. As the dislocations do not cut all the parti-

cles at the equator, the eﬀective diameter may be D

= πD/4, where D is

the average diameter of the spherical particles. Using the same value for D

as above, it follows that D

=11.8nm. For γ

APB

, this yields 0.090 J m

−2

for

screw dislocations, and 0.071 J m

−2

for dislocations with a large edge compo-

nent. These values are remarkably smaller than the literature values of about

0.15 J m

−2

(e.g., [466]).

The force balance at the trailing dislocation (8.4) can be written as

=(τ

− τ) b/γ

APB

According to Table 8.2, for the screw dislocations, τ

<τ,thatis,D

becomes negative. That means, the dislocations of a pair of screws are not

so strongly coupled as the model predicts. According to the latter, the trail-

ing dislocation has to bow out in backward direction, which, however, has

not been observed in the micrographs of the present study. On the contrary,

many trailing dislocations are clearly visible bowing out forward. For the edge