Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

190 5 Dislocation Kinetics, Work-Hardening, and Recovery

by measuring their local curvature, as discussed in Sect. 3.2.7. With (3.14),

(3.38), and (3.42), the relation between the eﬀective stress τ

∗

and the local

radius of curvature r can be written as

∗

(β)(ln(l/r

)+C)

r(β) b

, (5.17)

where Γ

(β) is the elastic part of the line tension. It can be calculated by

anisotropic elasticity theory with the formulae for straight dislocations. For

isotropic solids, it is Γ

(β)=μb



1+ν −3ν sin



/ (4π(1 − ν)).

A suitable method for determining the curvature of bowed dislocation

segments consists in comparing the images of the dislocation segments with

calculated dislocation loops of diﬀerent size. The eﬀective stress is then

∗

(ln(l/r

)+C)

(ln(l/r

)+C)

, (5.18)

with E

and E

being the elastic (prelogarithmic) parts of the line energy of

edge and screw dislocations, and x

the half-axis of the loop in the direction

of the Burgers vector and y

perpendicular to it. x

corresponds to e in the

case of isotropic elasticity.

For most materials, the elastic part of the line tension or energy is known

quite accurately. The problem is the logarithmic factor with the segment

length l, the inner cut-oﬀ radius r

, and the numerical constant C.Bothl

and C depend on the particular dislocation conﬁguration because of the self-

interaction between the curved segment under consideration and its adjoining

segments. In the line tension approach, this self-interaction can be considered

only by suitably choosing l and C. Reasonably well deﬁned is the conﬁguration

of a dislocation pinned by localized obstacles. As discussed in Sect. 3.2.7, l is

then the segment length of the bow-out. For half and full loops, l is the diam-

eter of the loops. Not well deﬁned are long dislocations bowing out between

cell walls or other sources of internal stress. Unfortunately, the conﬁguration

inﬂuences also the ratio between the radii of curvature of edge and screw

segments. To each conﬁguration, a diﬀerent constant C has to be applied. In

general, the straighter the conﬁguration is, the smaller is C (more negative).

To avoid this problem, some authors try to determine the line tension

experimentally. According to Albenga’s law, the spatial average of the internal

stresses has to vanish so that the average of the local stresses equals the applied

stress, that is,

τ

loc

(x, y) = τ =



loc



In [309], this procedure was applied separately to near-edge and near-screw

dislocations to ﬁnd the line tensions Γ of edges and screws. This method

5.2 Work-Hardening and Recovery 191

Table 5.2. Comparison of the macroscopic shear ﬂow stress of two MgO single

crystals with the eﬀective stresses determined from dislocation curvatures measured

by a photometric method. Data from [204]

Macroscopic From e, l,and From

ﬂow stress C = −1.61 M

39.0 125 50.6

42.6 111 56.4

implies the problem that the moving dislocations will stay in the regions of low

eﬀective stress so that their average will not represent the true spatial average

of the local stresses. If it did, there would not be any sense in measuring the

eﬀective stress as its average always had to be equal to the applied stress.

A detailed study of the radii of curvature of dislocation segments bowing

out between localized obstacles was performed based on the results of in situ

straining experiments in an HVEM on MgO single crystals [104], as described

in Sect. 3.2.7. From the local radii of curvature measured by a photometric

analysis of the dislocation contrast proﬁles, the major half-axes of correspond-

ing ellipses were calculated. The eﬀective stresses are then given by (3.45)

either from sets of e and l using the theoretical constant C = −1.61, or from

the slope M of the e vs. ln l diagrams, which corresponds to the experimental

constant C = −5.19. The parameters r

=0.4 b [114] and E

=1.03×10

−9

were used. Some data are collected in Table 5.2 together with the macroscopic

shear ﬂow stresses. Because of radiation hardening and a possible size eﬀect,

the ﬂow stresses in the in situ specimens may be about 30% higher than

the macroscopic ones [334]. The table shows that the data from the curvature

measurements using the theoretical constant C = −1.61 do not agree with the

macroscopic ﬂow stresses, whereas those with the experimental value of the

logarithmic factor of the line tension do. The data in the ﬁrst line of Table 5.2

refer to an experiment where the specimen was unloaded and reloaded and,

in addition, the curvature of many segments in the same specimen area was

measured by ﬁtting ellipses to the bowed-out segments. The load measured on

the in situ stage was scaled by the macroscopic ﬂow stress. Of these additional

measurements, Fig. 5.28 presents the relation between the average eﬀective

stress τ

∗

, calculated with the experimental constant C = −5.19, and the

shear stress τ, followed from the specimen load without considering radiation

hardening. The eﬀective stresses are smaller than the macroscopic ones, as it

is expected, as the dislocations stay mostly in regions of low eﬀective stress.

Within the accuracy of this experiment, both stresses are proportional to each

other. The diﬀerences between the data in the table and those in the ﬁgure are

certainly not due to the diﬀerent methods of determining the curvature but

rather to the choice of the segments to be evaluated. In the table, well bowed-

out segments were chosen for the photometric evaluation, whereas most of the

segments were evaluated by ﬁtting ellipses to the segments. This underlines the

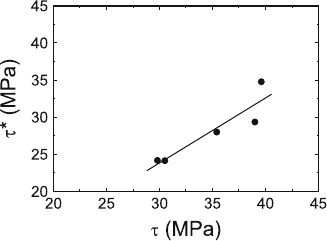
192 5 Dislocation Kinetics, Work-Hardening, and Recovery

Fig. 5.28. Dependence of the eﬀective stress on the applied stress in an MgO single

crystal taken during a loading series of an in situ straining experiment in an HVEM.

Dislocation curvatures measured by ﬁtting ellipses to the bowed-out segments. The

applied stress is not corrected for radiation hardening. Data from [204]

problem of a proper choice of curved segments for determining the eﬀective

stress. The latter shows a relatively wide symmetric frequency distribution

with a standard deviation of Δτ

∗

≈ 30 MPa. This scattering reﬂects only

partly the varying eﬀective stress but also the inﬂuence of the self-stress of

the neighboring segments on the curvature of the segment considered.

Summarizing, it may be stated that it is very diﬃcult to measure the

internal stresses. A rough estimate can be obtained by counting the disloca-

tion density and applying the Taylor equation (5.11). The importance of the

internal stresses is well recognized in studies of work-hardening. However, in

phenomena controlled by the mobility of dislocations like the low-temperature

deformation (e.g., [335]) or the ﬂow stress anomaly in intermetallic alloys

(Sect. 9), the inﬂuence of the internal stresses on the total ﬂow stress is widely

neglected.

5.2.4 Steady State Deformation

A combination of the dislocation kinetics controlling the evolution of the

dislocation structure and accordingly also the internal stress with the dis-

location dynamics, that is, the relation between the dislocation velocity and

the eﬀective stress, may serve as the basis for a system of constitutive equa-

tions governing the plastic deformation. As introduced in this book, the set

of equations may have the following form where, of course, alterations will be

necessary to describe the deformation in particular materials or in particu-

lar ranges of temperature and strain rate. In Sect. 10.5.7, the equations will

be applied to the high-temperature deformation of i–Al–Pd–Mn single qua-

sicrystals by the climb motion of dislocations. They are therefore formulated

in terms of normal stresses σ and strains ε.

5.2 Work-Hardening and Recovery 193

These equations are the following:

The kinetic equation of the dislocation density (5.8)

d

= wσ

∗

v

− q

where, at high temperatures, the annihilation coeﬃcient q will be a function

of temperature (5.9)

q = q

exp (−ΔG

ann

/kT ) ,

and the dynamic equation, for example, in the form of the (slightly simpliﬁed)

power law (4.103)

= v

exp



−

ΔG



∗m

These equations have to be supplemented by the relation between the

applied stress and the athermal and thermal ﬂow stress components (5.15)

σ = σ

+ σ

∗

the Taylor equation for the internal stress (5.11)

= α

μb

2π

√

,

the machine equation (2.5)

˙ε

=˙ε

+˙ε =˙σ/S +˙ε,

and the Orowan equation between the plastic strain rate and dislocation

velocity and density (3.5)

˙ε = bv

This set of equations considers all dislocations to be mobile, thus being

restricted to small plastic strains where immobile dislocation structures do

not yet form.

The above equations describe the evolution of the dislocation density at

the beginning of a deformation test. For a constant total strain rate ˙ε

and a

small initial dislocation density 

, the stress increases almost linearly with

time, σ ≈ S ˙ε

t, where the internal stress σ

is small almost up to the yield

point. After the yield point is passed, the deformation achieves a steady state

where hardening is compensated by recovery.

For applying the model to the temperature and strain rate dependence of

the steady state deformation of i–Al–Pd–Mn single quasicrystals (Sect. 10.5.7),

the steady state solution is found in analytical form [336]



m/(2m+1)

194 5 Dislocation Kinetics, Work-Hardening, and Recovery

and

= σ



1/(2m+1)

m/(4m+2)



. (5.19)

Here,



=(˙ε/ [v

exp (−ΔG

/kT )])

2/(m+2)

(w/S)

m/(m+2)

and

=(S ˙ε/ [wv

exp (−ΔG

/kT )])

1/(m+2)

are scaling factors of the dislocation density and the ﬂow stress, and D

and a are dimensionless parameters characterizing the eﬀects of recovery

D =(q/b)(w/ ˙ε)

(m−1)/(m+2)

−(2m+1)/(m+2)

exp (−ΔG

/kT )]

−3/(m+2)

and hardening a = αμ(bw/S)

1/2

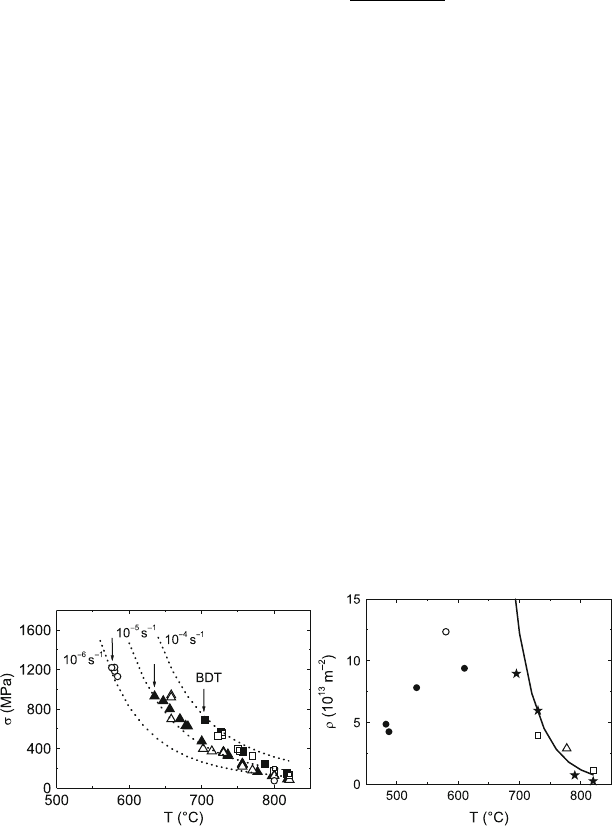
Figure 5.29 compares the calculations with the experimental data. The

parameters of the curves are the hardening factor α =2π, the stress expo-

nent m = 4, the activation energy of dislocation motion ΔG

=3eV,and

the activation energy of dislocation annihilation ΔG

ann

=4eV.Theactiva-

tion parameters ﬁt the data obtained by stress relaxation and temperature

change experiments. The remaining parameters v

and q

have been cho-

sen to make the dislocation density consistent with the values measured at

the lower yield point. The ﬁgure demonstrates that the model quite well

represents the temperature and strain rate dependences of the steady state

ﬂow stresses as well as the temperature dependence of the dislocation den-

sity. A closer inspection of the formulae reveals that the apparent activation

parameters are not equal to the model parameters. If the ﬁrst term in (5.19),

i.e., σ

∗

, dominates the deformation, then the apparent activation energy is

Fig. 5.29. Comparison of the steady state ﬂow stresses and the dislocation densities

of i–Al–Pd–Mn single quasicrystals with the results of the set of constitutive equa-

tions. (a) Temperature and strain rate dependence of the steady state ﬂow stresses.

Compression axes: twofold (open symbols), ﬁvefold (full symbols). (b) Temperature

dependence of the dislocation density. Data from steady state deformation (open

symbols), from work-hardening range (full symbols), dislocation density data from

[338] (asterisks). Strain rates ˙ε =10

−6

−1

(circles), 10

−5

−1

(triangles), 10

−4

−1

(squares). Curves: predictions of the model, arrows BDT: brittle-ductile transition.

Data from [336] and [337]

5.2 Work-Hardening and Recovery 195

ΔG

=2ΔG

− ΔG

ann

. If the second term, that is, σ

, is dominant, then

ΔG

=(ΔG

+ mΔG

ann

) /(m + 1). Thus, the model can explain a change in

the experimental activation energy with the increasing inﬂuence of recovery

at higher temperatures. Similarly, also the apparent stress exponent is not

equal to m of the dislocation mobility.

Steady state deformation conditions can be attained in experiments at a

constant strain rate as well as under constant load. The latter experiments

are called creep tests where the steady state range corresponds to a minimum

in the creep (strain) rate. A prerequisite to a steady state range is that the

dislocation density recovers, which balances the generation of new dislocations

during straining. Thus, steady state deformation is mostly restricted to higher

temperatures where diﬀusion allows climb and dislocation annihilation. The

steady state strain rate in single crystals can frequently be described by the

phenomenological equation

˙ε = A

μb





= A

μb

exp



−

ΔG





. (5.20)

A is a dimensionless factor, D is the diﬀusion coeﬃcient as in (4.86) with the

pre-exponential factor D

and the activation energy ΔG. The other quantities

have their usual meaning. There may be very diﬀerent processes controlling

steady state creep, dislocation motion controlled by glide or climb, climb of

dislocations in a three-dimensional network, and many others. An early review

is given in [339]. The paper [340] lists a great number of references on the mech-

anisms and experimental data on ceramics. A review on the behavior of metals

is given in [341]. The diﬀusion coeﬃcient may be that of self-diﬀusion or pipe

diﬀusion along dislocations. The stress exponents n are between about 2 and

6 with preference values around either 5 or 3. n ≈ 5 mostly occurs in pure

metals, and n ≈ 3 in solid solution alloys. As stated earlier, dislocation recov-

ery and annihilation play an important role. In [342], the change from power

law creep according to (5.20) to a range, with the stress exponent increasing

and the activation energy decreasing with increasing stress, is explained by

a change from the annihilation of dipole-like conﬁgurations by climb to that

by glide-controlled dislocation reactions. In polycrystals, creep is frequently

controlled by grain boundary processes.

Plastic deformation at high temperatures is certainly one of the most com-

plex processes of dislocation motion. Both its modes take place, glide, and

climb. They do not only carry the plastic deformation but they also realize

the recovery of the dislocation density. Frequently, the dislocations form a

relatively regular network where the motion of links in the network is gov-

erned by the link length like the moving branch of a Frank–Read source, for

example, in the model of [343], explaining a transition at decreasing tempera-

ture from climb-recovery controlled deformation to viscous glide governed by

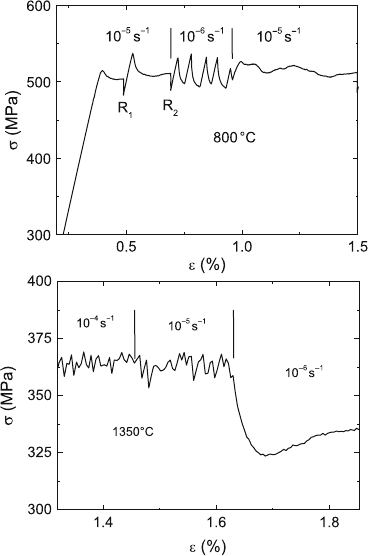
196 5 Dislocation Kinetics, Work-Hardening, and Recovery

Fig. 5.30. Sections of stress–strain curves of ZrO

-15 mol% Y

single crystals

containing changes of the strain rate from 10

−5

to 10

−6

−1

resulting in changes of

the stability state. (a) 800

◦

C. R

and R

are stress relaxation tests. (b) 1,350

◦

Data from [344]

moving point defect atmospheres. The problem is that many processes involve

lattice diﬀusion so that the experimental identiﬁcation of the mechanisms is

quite diﬃcult.

5.3 Plastic Instabilities

Up to this point, plastic deformation has been treated as a stable process, that

is, the stress–strain curve has been considered smooth. This is very frequently

the case but there are also exceptions in certain temperature and strain rate

ranges where the stress–strain curve shows regular or irregular drops and

re-increases, which is called jerky ﬂow or serrated yielding. Figure 5.30 illus-

trates the inﬂuence of the strain rate on the stability of deformation in ZrO

single crystals. At two temperatures, the strain rate is changed from 10

−5

to 10

−6

−1

. At the lower temperature of 800

◦

C (Fig. 5.30a), the deforma-

tion changes from stable to unstable, but at 1,350

◦

C (Fig. 5.30b) it changes

5.3 Plastic Instabilities 197

in the opposite direction. Similarly, the instability ranges and the shape of

the serrations depend on the temperature. The latter is demonstrated in the

stress-time records of Fig. 5.31. Figure 5.31a taken at 860

◦

C is characteristic

also of higher temperatures. First, the stress increases linearly, with the slope

equalling that of the elastic line as measured during unloading, for instance.

The elastic slope is indicated by the straight line. Thus, the loading takes place

as purely elastic deformation. When a certain stress level is reached, plastic

deformation sets in at a high rate with an abruptly decreasing load. At lower

temperatures, plastic deformation does not start at a very high rate so that the

unloading parts of the load-time curve get curved similarly to those of stress

relaxations, as shown in Fig. 5.31b for 800

◦

C. At an even lower temperature

in Fig. 5.31c, also the loading parts become rounded at their tips, which indi-

cates plastic deformation even during loading. In general, instability ranges

can be described in a plot of strain rate vs. temperature where instabilities

occur in limited regions.

Plastic instabilities are systematically classiﬁed in [345], according to which

they may occur by strain softening, by a negative strain rate sensitivity

(strain rate softening instabilities), or by localized heating (thermomechanical

instabilities). Strain softening may occur, for example, when the moving dislo-

cations destroy ordered states in alloys. Strain rate softening instabilities are

frequently connected with the Portevin–LeChatelier (PLC) eﬀect [346, 347]

due to dynamic strain ageing described in Sect. 4.11. Thermomechanical insta-

bilities result from a reduction of the ﬂow stress owing to local heating in slip

bands at low temperatures.

Plastic instabilities are discussed theoretically at diﬀerent degrees of

sophistication. Early linear stability analyses of a constitutive model of plas-

tic ﬂow by Kubin and Estrin [345, 348–350] have been extended by including

transient eﬀects, as reviewed by Zaiser and H¨ahner [351], as well as by the

evolution of the mobile and forest dislocation densities [352]. According to

[351], a change in the ﬂow stress can be written as

dσ = Θdε + rdln ˙ε +dσ

, (5.21)

where Θ is the work hardening coeﬃcient and dσ

is a change in the ﬂow stress

due to the relaxation of an internal parameter φ which, after a change in the

deformation conditions, attains a new quasi-steady state value after a charac-

teristic time t

. Including dσ

takes into account the transient eﬀects observed

experimentally after changing the deformation conditions as described in

Sect. 2.1, for example, the diﬀerence between the instantaneous and steady

state stress increments Δσ

and Δσ

in strain rate cycling tests, or the dif-

ference between an original and a repeated stress relaxation. With a linear

approximation of the relaxation process, a linear stability analysis yields the

condition for unstable deformation [351]

− r

˙ε (Θ − σ)

. (5.22)

198 5 Dislocation Kinetics, Work-Hardening, and Recovery

Fig. 5.31. Sections of stress-time records of ZrO

-15 mol% Y

single crystals in

the instability range at 10

−6

−1

.(a) Abrupt transitions between elastic and plastic

deformation and vice versa at 860

◦

C. At lower temperatures, temperature-dependent

plastic deformation develops. (b) 800

◦

C. (c) 780

◦

C. Data from [344]

=Δσ

/Δln ˙ε and r

=Δσ

/Δln ˙ε are the instantaneous and steady

state strain rate sensitivities. This more general stability criterion includes the

criteria of the simpler theories as approximations under simplifying conditions.

Assuming a short relaxation time t

so that

5.3 Plastic Instabilities 199

˙ε (Θ − σ)



instability occurs for r

< 0atΘ −σ>0. This is equivalent to the adiabatic

solution of the constitutive equation (5.21), that is, by canceling the term dσ

and setting r

= r. These kinds of instabilities are called strain rate softening

instabilities, which may occur if r

is negative, but not r

,whichisalways

positive. The inequality (5.22) can also be written as −r

˙ε(Θ − σ),

where t

˙ε =Δε

. It can be fulﬁlled not only by suﬃciently negative values

of r

, but also by suﬃciently negative values of Θ − σ. The latter kinds of

instabilities are called strain softening instabilities.

The diﬀerent physical processes causing strain rate softening instabilities

can be discussed by assigning diﬀerent physical variables to the structural

parameter φ. One possibility is to identify φ with the local specimen temper-

ature T ,asanincreaseinT yields an increase in the strain rate because of

the thermally activated character of the plastic deformation. Thus, instabili-

ties may occur by a feedback between the heat locally released by the plastic

deformation and the resulting increase in the strain rate. These instabilities

are called thermomechanical instabilities, being a particular case of the strain

rate softening instabilities.

In many cases, the plastic instabilities are of the strain rate softening type.

As discussed above, the simple theories then require that r

< 0forΘ−σ>0.

Frequently, however, r

is small but not negative. The following shows that

this criterion is relaxed in the more sophisticated theory in [351]. In alloys,

serrated yielding owing to strain rate softening is frequently connected with

diﬀusion processes of alloying elements in the stress ﬁelds of the dislocations.

This is called dynamic strain ageing as it reduces the dislocation mobility and

gives rise to the Portevin–LeChatelier eﬀect [346, 347]. The formation and

dragging of a dynamic cloud of point defects around a moving dislocation was

treated in Sect. 4.11.

The models of the Portevin–LeChatelier eﬀect reviewed in [351] use a

diﬀerent approach. The dislocation motion is assumed to be jerky on a meso-

scopic scale owing to obstacles to glide, which are overcome by stress-assisted

thermal activation. During the waiting time at the obstacles, the dislocations

are gradually aged by the formation of the solute clouds, leading to an increase

in the activation energy of dislocation motion, which depends on the waiting

time t

at the obstacles [353–355]. According to [356], the Gibbs free energy

of activation can be expressed as

ΔG =ΔF − Vτ

∗

+Δg (1 − exp [−(ηt

)

]) . (5.23)

Like in (4.101), ΔF , V ,andτ

∗

are the stress depending free energy of acti-

vation, the stress dependent activation volume, and the eﬀective stress. Δg is

the increase in the activation energy owing to ageing, t

the time constant of

ageing, and n an ageing exponent. ΔF and V are supposed to describe the

temporary pinning of the dislocations, which is caused by processes diﬀerent