Messerschmidt U. Dislocation Dynamics During Plastic Deformation

Подождите немного. Документ загружается.

180 5 Dislocation Kinetics, Work-Hardening, and Recovery

the dislocations passing by on parallel planes and, for multiple slip, by cutting

the debris. As the stress ﬁeld of ﬁnite dipoles decreases rapidly with increasing

distance, it is suggested that the debris acts similarly to precipitates. Accord-

ing to [311], the force between a dislocation and a nonparallel dipole is small

as long as the dislocation is not located between the dipole arms. The passing

of terminated dipoles by dislocations moving in an oscillating stress ﬁeld is

simulated in [312]. The dipoles may be annihilated or moved resulting in the

formation of dipole clusters. In general, the mechanism of debris hardening is

not well understood. The contribution to the ﬂow stress is probably mostly

small.

5.2.2 Thermal and Athermal Components of the Flow Stress

As described in the foregoing section, the grown-in dislocations and the dis-

locations stored in diﬀerent structures during plastic deformation cause a

ﬁeld of spatially varying long-range internal stresses. These stresses promote

the dislocation motion in some regions but impede it in others. Thus, these

stresses represent also obstacles to dislocation glide. According to Albenga’s

law, the spatial average of the internal stresses is zero. It has been discussed in

Sect. 4.1 that at a ﬁnite temperature the dislocation motion can be supported

by thermal activation. However, thermal activation is conﬁned to processes

where the energy necessary to surmount the obstacle at the actual stress is

less than about 40 kT, corresponding to about 1 eV at room temperature, and

where the volume involved contains less than a few hundred atoms. To move

a dislocation segment of length Δy in the long-range stress ﬁeld over a dis-

tance Δx against an internal stress τ

requires an energy of ΔxΔyτ

b.With

Δx =Δy =0.5 μm, τ

=10

−3

μ, b =3×10

−10

m, and μb

= 5 eV, the energy

becomes several thousand electron volt in contrast to 40 kT ≈ 1eV at room

temperature. Thus, this energy is far too high to be overcome by thermal

activation. Likewise, also the number of involved atoms is far too high. As a

consequence, long-range internal stress ﬁelds cannot be overcome by the action

of thermal activation. It is therefore useful to distinguish between components

of the ﬂow stress that can be surmounted by the aid of thermal activation

and those which cannot. The ﬁrst ones, the thermal components, result from

most mechanisms with short-range stress ﬁelds discussed in Chap. 4. Their

temperature dependence is of Arrhenius type and depends on the particular

interaction potential. The second ones, the athermal components, originate

from the long-range internal stress ﬁelds and some other processes requir-

ing high energies and being not restricted to small volumes like the Orowan

process. In this case, the temperature dependence is weak. It equals that of

the shear modulus as the interaction stresses are proportional to it (or per-

haps some other elastic constant). Accordingly, the thermal contributions to

the ﬂow stress are also denoted temperature-dependent components and the

athermal components temperature-independent ones. Figure 5.20 presents a

schematic plot of the superposition of long-range internal stresses (the sine-like

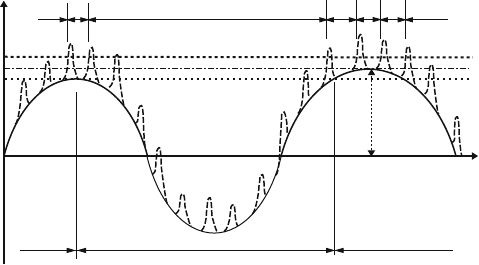
5.2 Work-Hardening and Recovery 181

–τ

i,loc

Δx

Fig. 5.20. Schematic drawing of the superposition of long-range internal stresses

and short-range interaction proﬁles

function) and the short-range ﬁelds of localized obstacles. These stresses are

plotted with negative sign. The internal stresses may be characterized by their

amplitude τ

and wavelength L. Three levels of the applied stress are char-

acterized by the horizontal lines τ

, τ

,andτ

. The local stress τ

loc

acting on

the short-range obstacles is given by the sum of the applied stress τ and the

local internal stress τ

i,loc

loc

= τ + τ

i,loc

. (5.14)

At ﬁrst, the situation may be considered without the presence of the short-

range obstacles. At zero external stress, the dislocation may be positioned at

the beginning of the τ

i,loc

vs. x curve. With increasing stress, the disloca-

tion moves forward along this curve. When the maximum τ

of the negative

(impeding) internal stress is reached at A, the dislocation can jump at a high

velocity to position B near the next maximum. As this maximum is higher

than that at A, the dislocation cannot surmount it. The only way to resume

the dislocation motion is to increase the stress again to the level of the maxi-

mum τ

. If the stress is high enough, the dislocation can pass all internal stress

maxima. This is a pure athermal motion of the dislocation. The situation is

similar for high temperatures, even if short-range obstacles are present. At a

suﬃciently high temperature, the waiting times at the obstacles will be very

short so that these obstacles do not impede the dislocation motion. In this

athermal situation, the jump distances of the dislocation Δx

will be given

by the wavelength of the internal stress ﬁelds.

At low temperatures, the waiting times at the short-range obstacles cannot

be neglected. At a stress level τ

, the dislocation coming from the left will

stop at the ﬁrst obstacle that exceeds the applied stress, marked by a thin

vertical line. After thermal activation, it moves to the next obstacle. When

this is overcome, the dislocation reaches a region of very high local stress,

where it ﬂies to the next maximum of the impeding internal stress. There, the

182 5 Dislocation Kinetics, Work-Hardening, and Recovery

obstacles again have to be surmounted individually by thermal activation. The

jump distances Δx

are now the distances between the short-range obstacles,

except in regions where the dislocation does not feel the short-range obstacles.

These regions become unimportant if the amplitude of the internal stresses is

small.

In summary, the kinematic behavior of the moving dislocations can be

characterized as follows. At intermediate temperatures, the dislocation motion

is governed by thermal activation and may be jerky on the small scale of local-

ized obstacles. If the Peierls stress is rate-controlling, the dislocation motion

may even be very smooth. The transition between the latter two mechanisms

was described in Sect. 4.6. At high temperatures, the localized obstacles are

overcome very quickly so that they do not control the dislocation motion. The

latter is governed by the long-range internal stress ﬁelds. It becomes athermal

and is jerky on the large scale of the wavelength of the stress ﬁelds. The tran-

sition between thermal and athermal behavior is not sharp. In more general

terms, the character of the dislocation movement is athermal if a great part of

the energy necessary to overcome the glide obstacles is supplied by the exter-

nal stress. In view of the force–distance curve of Fig. 4.1, a process is mainly

athermal if the work term ΔW comprises most of the total activation energy

ΔF , or if the Gibbs free energy of activation ΔG is small. This is expressed

also in Fig. 4.18, where the area swept after a single thermal activation event

increases strongly when the applied stress approaches the athermal ﬂow stress

of the obstacle array. In this sense, also dislocation motion at low tempera-

tures becomes athermal, because at the high stress level many obstacles are

overcome spontaneously. All these considerations are valid for temperatures

where diﬀusion can be neglected. At very high temperatures the dislocation

motion will become smooth again owing to the diﬀusion processes described

in Sect. 4.11.

As discussed in detail in Chap. 4, the actual dislocation velocity is a func-

tion of the local shear stress. The question arises as to the inﬂuence of the

internal stress ﬁelds on the average velocity of a dislocation moving under the

action of the macroscopic external stress τ and supported by thermal activa-

tion. A very simple argumentation goes back to Seeger [313]. The dislocation

spends most of its time in the regions of low local forward stress given by the

diﬀerence between the applied stress and the amplitude of the internal stress

ﬁelds, τ − τ

. Consequently, its average velocity will mainly be determined

by these jumps. In this model, the spatially varying local stresses and the

internal stresses are replaced by a constant so-called eﬀective stress τ

∗

and a

constant internal back-stress τ

. In contrast to (5.14) where the applied stress

and the varying internal stress add up to the local stress, now the eﬀective

stress is the diﬀerence between the applied stress and the internal stress

∗

= τ − τ

. (5.15)

This procedure had been adopted in most sections before. It is of highly

qualitative nature. It has to be expected that τ

is not equal to the amplitude

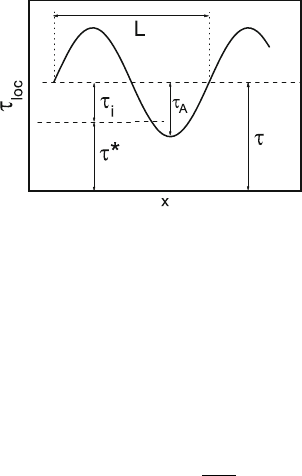
5.2 Work-Hardening and Recovery 183

Fig. 5.21. Model of a spatially periodic internal stress ﬁeld according to [315]

of the internal stresses τ

. A more sophisticated approach to the eﬀect of

internal stresses on the movement of dislocations is the calculation of the

average velocity of a dislocation moving in a spatially periodic internal stress

ﬁeld, as suggested by Chen et al. [314] and Li [315]. The latter is outlined here

as it has the advantage of an analytical solution. The locally acting stress τ

loc

is described by a sine function of the position x of the dislocation as illustrated

in Fig. 5.21, that is,

loc

= τ − τ

sin



2πx



Here, τ is the applied stress, τ

the amplitude, and L the wavelength of

the internal stress ﬁeld. It was shown in [316] that the internal stress ﬁelds

of periodic square arrays of screw dislocations of both the same sign and

of opposite sign can well be approximated by the sinusoidal function of the

position of the moving dislocation. In the calculations by Li, the instantaneous

velocity of the dislocation is given by the power law (4.10) or (4.103), in

abbreviated form

= Bτ

loc

The average velocity ¯v

is calculated by integrating 1/v

over one period L

and dividing the result by L. The analytical solution contains the Legendre

function. Figure 5.22 presents the dependence of the average velocity ¯v

nor-

malized by the velocity v

(τ,τ

= 0) at the same stress but without internal

stresses on the amplitude of the internal stress normalized by the applied

stress (τ

/τ). The average velocity is always lower than the velocity with-

out the internal stress ﬁeld. The deviations increase with increasing stress

exponent m.

The results can be compared with the simple model of a constant back

stress τ

= τ −τ

∗

discussed above by setting the average velocity equal to the

velocity at τ

∗

= τ − τ

¯v

= Bτ

∗

= B (τ − τ

)

may be called an apparent internal stress. It follows that

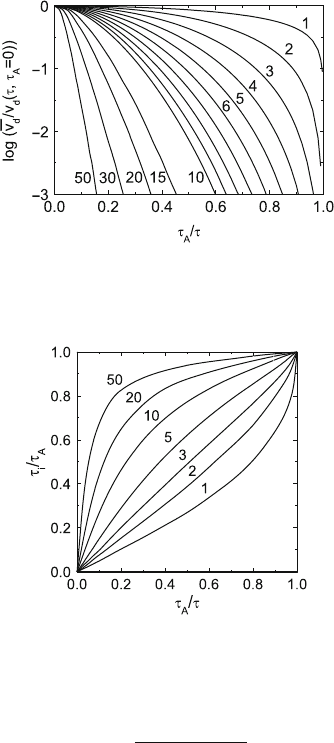
184 5 Dislocation Kinetics, Work-Hardening, and Recovery

Fig. 5.22. Dependence of the normalized average dislocation velocity in a peri-

odic internal stress ﬁeld on the amplitude of the internal stresses. Parameter: stress

exponent m. Data from [315]

Fig. 5.23. Dependence of the apparent internal stress on the amplitude of the

internal stresses. Parameter: stress exponent m. Data from [315]

= τ



1 −



¯v

(τ,τ

=0)



1/m



This relation is plotted in normalized form in Fig. 5.23. The apparent inter-

nal stress is lower than the amplitude of the internal stress ﬁelds τ

but

approaches it for τ

→ τ. The deviations are signiﬁcant only if both τ

and

m are small.

In general, the amplitudes of the internal stress ﬁelds are not known, nei-

ther are they constant as assumed here. For studies of the dislocation dynamics

by measuring the activation parameters during plastic deformation, the prob-

lem of the internal stresses is important as the formalism of the thermally

activated dislocation motion is based on the locally acting eﬀective stress, but

not on the applied stress. Using the diﬀerential techniques like strain rate

cycling or stress relaxation tests (4.9) and (4.11), one usually assumes that in

addition to the pre-exponential factor (e.g., ˙γ

in (4.8)) also the internal stress

5.2 Work-Hardening and Recovery 185

Fig. 5.24. Dependence of the normalized apparent activation volume on the

amplitude of the internal stresses. Parameter: stress exponent m. Data from [315]

remains constant so that ∂τ

∗

= ∂τ. However, that what remains constant dur-

ing an instantaneous change of the deformation conditions is not the apparent

internal stress τ

but the amplitude of the internal stress ﬁelds τ

. Accordingly,

the measured or apparent activation parameters like the activation volume

and the activation enthalpy have their well deﬁned thermodynamic meanings

but they do not represent the quantities occurring in the respective models.

Based on the calculation of the average dislocation velocity plotted in Fig. 5.22,

the plot in Fig. 5.24 shows the ratio between the apparent activation volume

app

(τ) measured at the stress τ and the activation volume V (τ

∗

) deﬁned

by the microscopic models measured at the stress τ

∗

. The apparent activa-

tion volume is always larger than the true one. The deviations increase with

increasing amplitude of the internal stress ﬁelds. However, they are mostly

less than a factor of two. They are small for high stress exponents m and for

low temperatures where τ

/τ is small. The relation between the true and the

apparent activation volumes was treated in a more general way in [317].

Similarly, also measurements of the stress exponent m = ∂ ln v

/∂ ln τ

∗

are inﬂuenced by the presence of internal stresses. The calculations show that

the apparent stress exponent m



= ∂ ln v

/∂ ln τ is always greater than m.

For high values of m, the eﬀect of the varying internal stress of amplitude τ

is almost equal to that of the presence of a constant back stress τ

= τ

.It

follows then for the apparent stress exponent



1 − τ

/τ

. (5.16)

In conclusion, the inﬂuence of the presence of spatially varying internal

stress ﬁelds on the experimental determination of the dynamic dislocation

properties cannot exactly be described by a constant internal back stress τ

However, as the properties of the internal stress ﬁelds are not well known, the

assumption of a locally constant back stress is suﬃcient for rough estimates

from experimental data. Nevertheless, it should be kept in mind that the

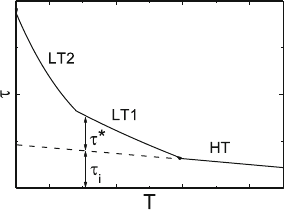
186 5 Dislocation Kinetics, Work-Hardening, and Recovery

Fig. 5.25. Schematic plot of the temperature dependence of the ﬂow stress in the

ranges where diﬀusion is not important

activation volume and the stress exponent related to the dislocation mobility

models are smaller than the apparent values obtained from experiments.

In a schematic way and if diﬀusion processes are neglected, the temper-

ature dependence of the ﬂow stress may look like that in Fig. 5.25. At high

temperatures (HT), the deformation is athermal. The ﬂow stress depends only

weakly on the temperature owing to the temperature dependence of the shear

modulus. Changing to lower temperatures may result in one or more ther-

mal ranges with stronger temperature dependencies, for example, LT1 with

localized obstacles and LT2 with the Peierls mechanism. It is very common

to extrapolate the athermal high-temperature range to low temperatures to

obtain the internal back stress τ

also for lower temperatures, as indicated

in the ﬁgure. However, this treatment is based on the supposition that the

internal structure remains constant at all temperatures. This may approxi-

mately be true if a specimen is deformed at a high temperature, then cooled

down to a low temperature and deformed again. In the general case where

individual specimens are deformed at diﬀerent temperatures, the dislocation

microstructure, in general, and the dislocation density, in particular, are dif-

ferent at each temperature. In the ﬁrst stage of deformation, the dislocation

density increases very rapidly. As the multiplication rate depends on the eﬀec-

tive stress (5.2), and this in turn on the temperature, the dislocation densities

at the yield point are expected to drastically increase with decreasing tem-

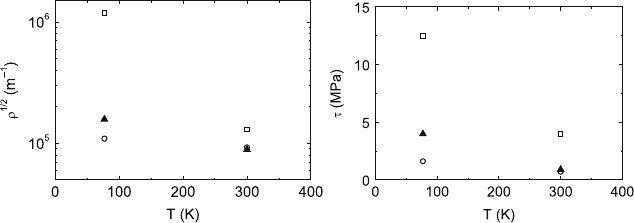
perature. This is shown in Fig. 5.26 using the data of NaCl single crystals

deformed at room and liquid nitrogen temperatures. The dislocation densities

are considerably higher in the crystals deformed at liquid nitrogen temper-

ature. Thus, the assumption that the athermal part of the ﬂow stress does

not, or only weakly, depend on temperature is generally not fulﬁlled. A better

approximation is certainly the validity of the Cottrell–Stokes law [318], that

is, the proportionality between the thermal and athermal ﬂow stress parts.

This law was originally formulated for the stress variation by work-hardening

but may apply also to other cases.

Most mechanisms described in Chap. 4 controlling the dislocation mobility

and causing a thermal contribution to the ﬂow stress do not depend on the

5.2 Work-Hardening and Recovery 187

Fig. 5.26. Dependence of the square root of the dislocation density and the (shear)

ﬂow stress on the temperature in deformed NaCl single crystals of diﬀerent divalent

impurity concentrations: 1.7 ppm residual impurities (open circles), 32 ppm Ca

(full triangles), 136 ppm Ca

(open squares). Data from [177]

plastic strain. However, in many materials also the thermal part of the ﬂow

stress increases during work-hardening, for example, being manifest by an

increasing strain rate sensitivity with increasing strain. There are only few

mechanisms explaining such a behavior. One of them is dislocation cutting

where part of the energy may be supplied by thermal activation. Frequently,

the obstacle distance obtained from the strain rate sensitivity is in the range

of the distance between forest dislocations and scales with the reciprocal stress

(e.g., [319]). The other possible mechanism is the interaction between moving

dislocations and debris. No detailed data as to this possibility are available yet.

In the literature, there are several attempts to link the dynamics of the

motion of individual dislocations with the continuum theory of plastic defor-

mation by the motion of many dislocations as it was founded by Kr¨oner [320].

Recently, Hartley [321] extended these theories by introducing a dislocation

density vector for a particular slip system, which describes the net length of

the dislocation lines with the same Burgers vector in the respective volume

element. The orientation of the vector is given by the ratio of the total length

of screw and edge components. Besides, a dislocation mobility tensor relates

the velocity of a dislocation conﬁguration in the volume element to the net

Peach-Koehler force on the conﬁguration. As an example, the cutting of a

forest dislocation is treated yielding a plastic potential to establish a ﬂow law.

5.2.3 Experimental Determination of the Stress Components

Several special sequences of changing the macroscopic deformation parameters

had been designed to determine the eﬀective stress. They will not be discussed

here in detail because of their restrictive assumptions involved. Looking at

Fig. 5.20, one may conclude that dislocation motion is possible only as long as

the applied stress is higher than the amplitude of the internal stresses, τ>τ

or, alternatively the applied stress is higher than the internal back stress,

τ>τ

. Thus, in a stress relaxation experiment, the relaxation rate should tend

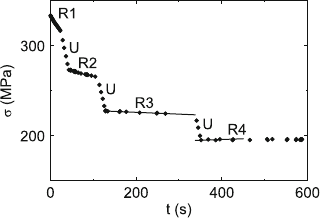
188 5 Dislocation Kinetics, Work-Hardening, and Recovery

Fig. 5.27. Stress dip test on a cubic zirconia single crystal deformed at 1,180

◦

consisting of short stress relaxations R

and partial unloadings U. Data from the

work in [324]

to zero when the stress reaches the athermal level. These long-time relaxation

tests require a very stable testing machine to record strain rates of the order of

−8

−1

. Because of (2.7), the relaxation time is short if the stiﬀness S of the

testing machine (plus specimen) is high. A high machine stiﬀness is reached by

electronic strain control. Nevertheless, even if the relaxation rate is low, there

may still be an appreciable eﬀective stress. The time of the experiment can be

reduced by so-called stress dip tests [322]. A recent application is described

in [323]. In these tests, the machine is stopped for a relaxation test. After

suﬃciently long recording to observe the actual relaxation rate, the stress is

reduced by partial unloading followed by another period of relaxation, and so

on. With decreasing load, the relaxation rate decreases but at a stress below

the athermal ﬂow stress, the relaxation rate changes its sign as the dislocations

rearrange and move backwards in the internal stress ﬁeld. In this way, it is

possible to approach the athermal stress level from both sides. An example

is shown in Fig. 5.27. Of course, one prerequisite to these methods is that

recovery does not take place during the time of the experiment.

In heterogeneous dislocation structures, the internal stresses can be studied

by X-ray diﬀraction. Changes in the lattice parameter as a consequence of

internal stresses cause an asymmetrical broadening of the diﬀraction proﬁles

because of the diﬀerent volume fractions of the hard and soft regions with their

diﬀerent internal stresses. This method has been applied to cell structures and

subgrain structures [325,326].

One way of estimating the athermal stress component also in homogeneous

dislocation structures consists in the determination of the dislocation density 

and the application of (5.11) with a suitable interaction constant α. The dislo-

cation density is deﬁned as the dislocation length per unit volume. Frequently,

it is measured as the number of points of dislocations emerging through the

unit area of an external surface or a cross-sectional plane of a deformed spec-

imen. The relation between both deﬁnitions depends on the slip geometry.

In most cases, setting the dislocation density equal to twice the density of

emergence points is a good approximation [327]. The points of dislocations

5.2 Work-Hardening and Recovery 189

emerging through surfaces can be marked by etching a cleavage or polished

surface as mentioned in Sect. 2.2. The etch pits can be observed by optical

microscopy up to a density of about 10

−2

. Replicas of smaller etch pits

produced by the heavy metal carbon shadowing technique can be observed

in the transmission electron microscope. This method allows one to count

representative values of intermediate dislocation densities up to 10

−2

Higher densities of dislocations are determined from diﬀraction contrast

TEM images of thin ﬁlms of the deformed samples. From the total projected

length Λ imaged within the area A, the dislocation density is calculated by

 =4Λ/(πAt) [328]. Here, t is the foil thickness, which can be determined from

the emergence points through both surfaces of a dislocation lying on a known

plane, or by other methods of diﬀraction contrast TEM. A simpler method

consists in superimposing a rectangular net of two sets of parallel straight lines

of nonconstant spacing onto the micrograph. The dislocation density is deter-

mined by counting the numbers of intersections N

and N

of the dislocations

along the two respective sets of grid lines. With the total lengths L

and L

of the grid lines, the dislocation density becomes  =(N

+ N

) /t

[329]. If randomly oriented lines are used, the dislocation density is esti-

mated by  =2N/(Lt) [330]. TEM extends the range of dislocation density

measurements up to about 10

−2

. It has to be considered, however, that

part of the dislocations may be invisible because of contrast extinction at the

particular imaging vector. Depending on the latter, in the f.c.c. lattice, the

fraction of the extinguished dislocations may amount up to 50%.

High dislocation densities can also be determined from the broadening

of X-ray diﬀraction proﬁles. A high sensitivity is necessary, which can be

achieved in the so-called self-focusing arrangement where the contribution

of the wavelength dispersion to the instrumental line-broadening disappears

[331]. The full width at half-maximum of the X-ray lines can be represented

by the modiﬁed Williamson–Hall plot [332] according to

ΔK ≈ 0.9/D +(π/2)

1/2

Mb

1/2

+ higher terms in K

where θ is the diﬀraction angle, λ the wavelength of the X-rays, K =2sinθ/λ,

and ΔK =2cosθ(Δθ)/λ. D is the particle or subgrain size, b is the magnitude

of the Burgers vector, and  is the dislocation density. Furthermore, M is a

constant depending on the outer cut-oﬀ radius of the dislocations, and C is

the dislocation contrast factor, which depends on the relative orientations

between the Burgers and line vectors of the dislocations and the diﬀraction

vector as well as on the elastic constants. For cubic crystals, C values have been

calculated in [333]. The contributions to the line broadening from the particle

size and from the strains due to dislocations can be separated by plotting

ΔK vs. KC

1/2

. The method has been applied, for example, to determine the

gradients in the dislocation density between the bulk and surface regions of

deformed crystals.

The most sensitive and spatially resolving technique is the measurement

of the eﬀective stress by using the dislocationsthemselvesasaprobe,thatis,