Mench M.M. Fuel Cell Engines

Подождите немного. Документ загружается.

c04 JWPR067-Mench January 28, 2008 17:28 Char Count=

150 Performance Characterization of Fuel Cell Systems

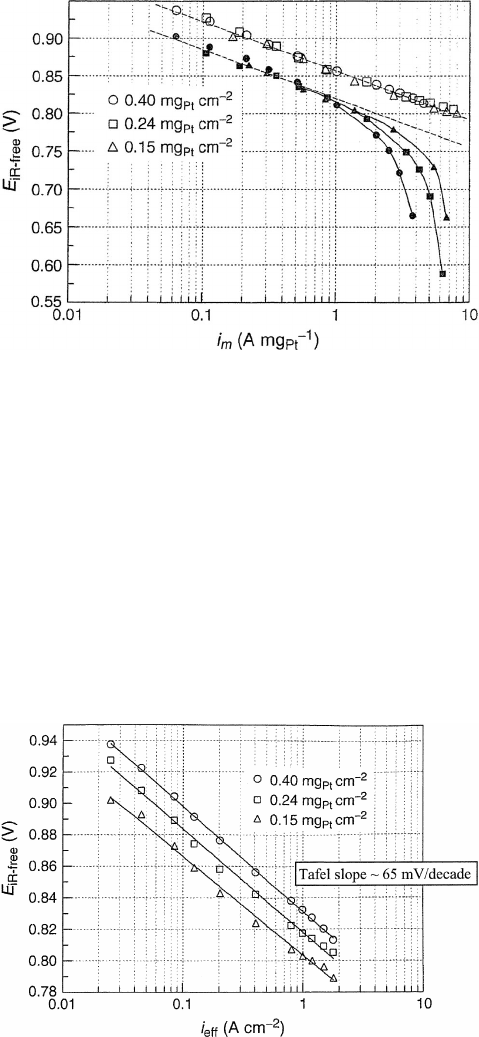
Figure 4.23 Experimental Tafel plot of cell voltage versus current, corrected for fuel cell ohmic

and other losses, so that only cathode polarization losses are remaining. The results are normalized

to platinum loading. Results with open circles are with humidiﬁed oxygen, and closed circles are

with humidiﬁed air. The dashed line represents the Tafel slope behavior. Note that for all loadings the

Tafel slope for oxygen reduction on platinum is the same but deviates from this behavior under mass-

limiting behavior. Also note that the vertical axis is ohmic corrected fuel cell voltage, not electrode

overpotential, so the voltage falls with increasing current density. (Reproduced with permission from

[9].)

Figure 4.23), since the opposing branch of the BV equation can no longer be neglected,

and the Tafel approximation is not valid. At very high current density, deviation is observed

experimentally due to concentration polarization effects. An experimental Tafel slope for

the ORR in a humidiﬁed H

fuel cell is shown in Figure 4.24. The data in Figure 4.24

were extracted from the polarization curves of fully humidiﬁed PEFCs operating on pure

Figure 4.24 Tafel plot for ORR current–overpotential curve. Data for a H

–O

PEFC at 80

◦

with different cathode catalyst loadings. The slope of the line (Tafel slope) for all conditions is

approximately 0.65 mV/decade. (Reproduced with permission from [9].)

c04 JWPR067-Mench January 28, 2008 17:28 Char Count=

4.2 Region I: Activation Polarization 151

Linearized

kinetics

region

Tafel kinetics

region

Slope breakoff

due to mass

transfer effects

log i

activation

Figure 4.25 Region of applicability for sinh BV simpliﬁcation.

oxygen and hydrogen at high stoichiometry. After correcting for measured ohmic losses,

one can measure the kinetics of a fuel cell in situ; however, careful ohmic correction and

pure, fully humidiﬁed reactants are needed to avoid concentration and other unaccounted

losses. For an electrode ex situ, Tafel measurements can be accomplished with the use of a

reference electrode and galvanostat/potentiostat to impose a desired voltage or current on

the working electrode.

Simpliﬁed Butler–Volmer Equation 3: Butler–Volmer Equation with Identical Charge

Transfer Coefﬁcients–sinh Simpliﬁcation A very nice simpliﬁcation can be made to

the BV model if the anodic and cathodic charge transfer coefﬁcients at the electrode are

equivalent (i.e., α

= α

). In this case, no approximation is needed, and a new form explicit

in η and mathematically equivalent to the original BV model can be written. This model is

valid over all regions of the electrode polarization, as shown in Figure 4.25.

If α

= α

= α, we can rearrange the BV equation into a general form:

cell

= i



exp



αF



− exp



−αF



= i



exp

−exp

−x



where x =

αFη

(4.47)

From mathematics

sinh

(

)

(exp

−exp

−x

) (4.48)

Comparing Eqs. (4.47) and (4.48), we can show that

cell

= 2i



exp



αF



− exp



−

αF



(4.49)

= 2i

sinh



αF



(4.50)

c04 JWPR067-Mench January 28, 2008 17:28 Char Count=

152 Performance Characterization of Fuel Cell Systems

Taking the inverse, we can show our desired expression:

η =

αF

sinh

−1



cell



(4.51)

Summary of Butler–Volmer Kinetics and Useful Simpliﬁcations

1. General kinetics, applicable under all current density conditions; the general BV

expression for η (solve numerically):

cell

= i



exp





− exp



−α



(4.52)

2. Low polarization, facile kinetics, linearized BV approximation (explicit η expres-

sion):

η =±

(

+ α

)

(4.53)

3. High polarization, Tafel approximation (explicit η expression):

η =





(4.54)

4. Both regions, α

= α

sinh simpliﬁcation (explicit η expression):

αF

sinh

−1



cell



= η (4.55)

Example 4.4 Selection of Proper Butler–Volmer Kinetic Model Solve for the most

appropriate symbolic expression for the activation overpotential at each electrode in the

given examples.

SOLUTION Case 1: Solid Oxide Fuel Cell On the anode, a pure hydrogen feed at

1000

◦

C is used with low losses. The cathode shows high losses but you can assume that

a,c

= α

c,c

At the anode: simpliﬁed model, facile kinetics, since no information on the charge transfer

coefﬁcient is given:

cell

= i

o,a





a,a

+ α

c,a





cell

o,a



a,a

+ α

c,a



At the cathode: simpliﬁed model, sinh simpliﬁcation, since α

a,c

= α

c,c

cell

= i

o,c

× 2sinh



αF



αF

sinh

−1



cell

o,c



= η

c04 JWPR067-Mench January 28, 2008 17:28 Char Count=

4.2 Region I: Activation Polarization 153

Case 2: Direct Methanol Fuel Cell At the anode and cathode, there are signiﬁcant

polarizations:

At the anode: simpliﬁed model, Tafel kinetics:

cell

= i

o,a



exp



a,a



⇒ η

a,a



cell

o,a



At the cathode: simpliﬁed model, Tafel kinetics:

cell

= i

o,c



−exp



−

c,c



⇒

c,c



cell

o,c



Case 3: Hydrogen PEFC At the anode the exchange current density is very high

with α

a,a

= α

a,c

. At the cathode i

∼ 1 × 10

−7

A/cm

and α

c,c

= α

a,c

At the anode: simpliﬁed model, linearized kinetics (we should check this assumption, as in

Example 4.1, with more information):

cell

= i

o,a





a,a

+ α

c,a





cell

o,a



a,a

+ α

c,a



At the cathode: simpliﬁed model, sinh simpliﬁcation:

cell

= i

o,c

2sinh



αF



αF

sinh

−1



cell

o,c



= η

COMMENTS: The sinh simpliﬁcation is generally preferred to the Tafel or lineraized BV

approximation if appropriate, since it is mathematically equivalent to the full BV equation.

Also, we should note the concentration effect is ignored here but can signiﬁcantly affect

the exchange current density through Eq. (4.31).

Example 4.5 Activation Polarization Loss Calculation Given the table below, solve for

the following:

(a) Using the appropriate kinetics, calculate the anodic activation overpotential (η

a,a

)

at 0.5 A/cm

(b) Using the appropriate kinetics, calculate the cathodic activation overpotential at

0.5 A/cm

Parameter Value

Temperature 363 K

(elementary charge transfer step) 1

(elementary charge transfer step) 1.2

a,a

0.5

a,c

0.5

◦

(T , P) 1.15 V

o,a

1.5 A/cm

o,c

0.005 A/cm

c04 JWPR067-Mench January 28, 2008 17:28 Char Count=

154 Performance Characterization of Fuel Cell Systems

SOLUTION (a) Calculate the anodic activation overpotential at 0.5 A/cm

(η

a,a

). The

linearized BV equation can be used since α

Fη/R

T < 0.15. Also, since in this case α

a,a

a,c

= βn

, sinh can be used:

αF

sinh

−1



cell

o,a



= η

a,a

8.314 × 363

0.5 × 96,485

sinh

−1



0.5

2 · 1.5



= 0.0104 V

(b) Calculate the cathodic activation overpotential at 0.5 A/cm

(η

a,c

). The Tafel BV

approximation can be used since α

Fη/R

T > 1.2:

c,c



cell

o,c



8.314 × 363

0.5 × 1.2 × 96,485



0.5

0.005



= 0.24 V

COMMENTS: The number of electrons transferred in the elementary charge transfer

step at the cathode, n

, can be a noninteger value if derived experimentally since there can

be more than one charge transfer reaction in parallel. The kinetic polarization voltages in

this example are typical relative to one another. That is, the ORR losses usually dominate

activation losses when pure hydrogen is used as the fuel.

Model Development Returning to our ultimate goal of this chapter to analytically model

the polarization curve, we now have an expression that includes the starting equilibrium

voltage from the Nernst equation (the top of the “waterfall”) and the departure from the

waterfall resulting from activation overpotential on the anode and cathode:

cell

= E

◦

(T , P) − η

a,a

−



a,c





 

Can now solve

−η

− η

m,a

−



m,c



− η

(4.56)

Next, we need to add ohmic, concentration, and other polarization losses before our model

is complete.

4.2.3 Langmuir and Tekmin Model of Kinetics

For an electrochemical reaction to take place, the reacting species must ﬁrst undergo

adsorption or chemisorption onto the reacting surface followed by an intermediate reaction

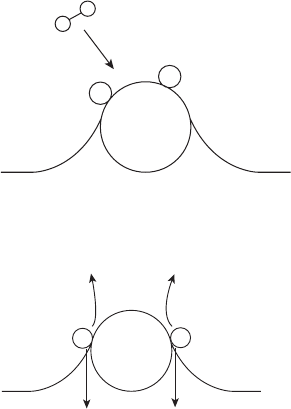
to an activated complex, as depicted in Figure 4.26. For example, consider the following

HOR mechanism intermediate reactions:

 2

(

H − M

)

(4.57)

(

H − M

)

 H

+ e

−

(4.58)

For the charge transfer to take place at the catalyst surface, the reacting species is ﬁrst

adsorbed onto the catalyst, in this case dissociating in the process into separately adsorbed

hydrogen atoms. Here, M indicates the adsorbing catalyst surface. After adsorption, the

charge transfer reaction can take place.

In BV modeled reactions, the intermediate charge transfer steps are rate limiting, and

the adsorption is comparatively facile and rapid. However, this is not always the case. In

This section can be skipped without loss of continuity.

c04 JWPR067-Mench January 28, 2008 17:28 Char Count=

4.2 Region I: Activation Polarization 155

Catalyst

Surface

Ionomer

(a)

Step 1: Dissociative

chemisorption

of hydrogen

Catalyst

surface

Ionomer

Step 2:

Electro-oxidation

(To cathode)(To cathode)

–

(To Bipolar plate)

(b)

Figure 4.26 Schematic of electrochemical reaction and absorption.

some situations, the rate-limiting step can be the surface adsorption or chemisorption of the

reacting species onto the catalyst sites. Certain situations in fuel cells can be characterized in

this fashion. Speciﬁcally, this can be important where a catalyst poison interferes with the de-

sired reaction. As an example, when hydrogen containing part-per-million levels of carbon

monoxide is introduced into the anode of a low-temperature PEFC, the carbon monoxide

electro-oxidative desorption from the catalyst is very slow relative to the carbon monoxide

adsorbtion and the hydrogen electro-oxidation reactions. The key rate-limiting reaction is

believed to be the electrochemical oxidative desorption of CO from the catalyst site [11].

O + (M − CO) −−−−−→M + CO

+ 2H

+ 2e

−

(4.59)

Other similar cases exist, such as direct electro-oxidation of alcohols such as methanol

and formic acid in low-temperature fuel cells. In these cases, an alternative to the

BV formulation that accounts for the limiting adsorption and charge transfer steps is

appropriate. Two common models for a surface adsorption limited reaction are the

Langmuir and Temkin kinetics. In the simpler Langmuir model, the surface adsorption

rate constant is independent of surface coverage. In the Temkin model, the adsorption rate

constant is modeled as a function of the surface coverage of adsorbed species. In both

models, a two-step reaction mechanism is assumed [6]:

1. A surface adsorbtion/desorbtion reaction, one or both of which are rate determining.

2. An electrochemical reaction responsible for ion exchange and current generation

that is assumed to be much faster than the adsorbtion/desorbtion step. In addition,

the reaction is assumed to occur so fast that the reverse reaction is assumed to be

negligible.

c04 JWPR067-Mench January 28, 2008 17:28 Char Count=

156 Performance Characterization of Fuel Cell Systems

This two-step mechanism can be expressed as

R + M

1 f



(

R − M

)

(rate limiting) (4.60)

(

R − M

)

2 f

−−−−−→ R

+ ne

−

(relatively fast) (4.61)

Where k

, and k

represent the adsorbtion and desorption reactions (which can be physical

or chemical), respectively, and R represents the molar gas-phase concentration of the

reacting species. The k

reaction represents the fast-forward ion charge transfer reaction of

the adsorbed species responsible for the current generation, and it is assumed the reverse

reaction is negligible. It should be noted that other species or parallel reactions can also be

included in the above formulation methodology. If θ represents the fraction of the available

catalysis sites that the adsorbed species occupies, we can then write

dθ

= k

1 f

(

1 − θ

)



 

−k



−k

2 f





III

(4.62)

Term I represents the adsorption of species R onto the remaining noncovered reaction sites.

If θ becomes 1, representing uniform surface coverage, the adsorption obviously stops. The

partial pressure of species R (y

P) is also included in Eq. (4.62) since the adsorption from

the gas phase is proportional to the concentration in the gas phase.

Term II represents the desorption of the adsorbed species from the reactive surface

and decreases the surface coverage. Term III is the forward electrochemical ionization

reaction responsible for current ﬂow. From inspection of Eq. (4.62), in the case of an

adsorption-limited reaction, the kinetic limiting current density should be the maximum

possible adsorption rate where the surface coverage θ becomes zero, or

lim

∝ k

1 f

(

1 − θ

)

− k

θ − k

2 f

θ ∝ k

1 f

P (4.63)

The constant of proportionality is the electrons per mole of reactant, nF,or

lim

= nFk

1 f

P (4.64)

so that, for an adsorption-controlled reaction, the limiting current density is linearly pro-

portional to the gas-phase partial pressure, and adsorption rate constant k

can be either

assumed to be constant (Langmuir model) or a function of the surface coverage (Temkin

model). Here, we will show solution for the Langmuir model. The reader is referred to

advanced electrochemistry texts for additional details on Temkin kinetics [e.g., 12].

The overall electrochemical reaction rate can be shown as

i = nFk

2 f

θ (4.65)

Using this two-step model, which can be expanded to include other intermediate steps

as well, a simple formulation for the electrode overpotential current relationship at a

given electrode can be developed. If we assume that the reaction rate constants involved

are independent of the surface coverage of reactant R, then we can derive the Langmuir

kinetics model solution. With constant rate constants in Eq. (4.62), at steady state we can

c04 JWPR067-Mench January 28, 2008 17:28 Char Count=

4.3 Region II: Ohmic Polarization 157

show that

dθ

= 0 = k

1 f

(

1 − θ

)

− k

θ − k

2 f

θ (4.66)

Then, solving for surface coverage, we can show, from algebraic manipulation, that

θ =

1 f

2 f

+ k

1 f

(4.67)

Physically, this shows the surface coverage fraction is simply the ratio of the adsorption

reaction to the total sum of parallel reactions. Then the current density i becomes

i = nFk

2 f

θ = nFk

2 f



1 f

2 f

+ k

1 f



(4.68)

Now we seek to relate this expression to the overpotential required to produce that current

density at the electrode of interest, so that we can predict electrode overpotential as a

function of current density in a similar fashion as with the BV approach for electron-

transfer-limited reactions. The electrochemical reaction rate constant k

can be written

2 f





exp



αnF



(4.69)

where i

is the exchange current density at θ = 1. Using Eq. (4.68), we can achieve our

desired result, an explicit expression for electrode overpotential as a function of current

density and other measurable parameters for an absorption-limited electrochemical reaction

under the Langmuir model:

η =

αnF





+ k

1 f





nRk

1 f

P − i





(4.70)

The reaction rates required for solution would be determined from existing literature or

from direct experimental results.

4.3 REGION II: OHMIC POLARIZATION

At moderate current densities, a primarily linear region is evident on the polarization curve

in Figure 4.1. In region II, reduction in voltage is dominated by internal ohmic losses

(η

) through the fuel cell, resulting in the nearly linear behavior, although activation and

concentration polarization in this region are still present. The ohmic polarization can be

represented as

= iA





k=1



(4.71)

where each r

value is the area-speciﬁc resistance of individual cell components, including

the ionic resistance of the electrolyte, and the electric resistance of bipolar plates, cell

c04 JWPR067-Mench January 28, 2008 17:28 Char Count=

158 Performance Characterization of Fuel Cell Systems

= Linear path of ion travel

A = Cross-sectional area

ρ=

= Ω-m

Figure 4.27 Schematic of ion travel in conductor.

interconnects, and contact resistance between mating parts and any other cell components.

For most fuel cell types at the beginning of operating life, ohmic polarization is dominated

by ionic conductivity in the main electrolyte and in the catalyst layers. Electronic resistance

is typically relatively low, unless there are aging or assembly/contact issues.

Electronic and Ionic Resistance To solve ohmic resistance problems, some basic tools

are required. First, Ohm’s law can be written

V = IR = iAR (4.72)

where R is the resistance, measured in units of ohms ( = Js/C

), and A is the electrode

geometric surface area. The resistance is a function of the geometry of the conducting

material. The resistivity ρ is an intrinsic property of a material related to the resistance

through the cross-sectional area of ion travel, A, and the linear path length of ion travel, l,

as shown in Figure 4.27.

Resistance and resistivity are terms typically used to describe ohmic drop in materials

that have signiﬁcant resistance. For materials with very low ionic resistivity, the inversely

related conductance G and conductivity σ are commonly used. By deﬁnition

σ = conductivity =

= 1/ m = S/m (4.73)

G = conductance =

= 

−1

= S (4.74)

and Ohm’s law, Eq. (4.72), can be shown as

V = iA

σ A

= iρl (4.75)

Table 4.3 shows some typical conductivity values for selected fuel cell materials. Note

the dominance of the ionic conductivity of the electrolyte. The functional dependence of

electrolyte conductivity for various fuel cells is covered in Chapter 5.

From a basic understanding of Ohm’s law, we can identify the critical factors governing

these ohmic losses in a fuel cell:

1. Material Conductivity The electrolyte and catalyst layer should have the highest

possible ionic conductivity and all other components including the catalyst layer

should have the highest possible electrical conductivity.

c04 JWPR067-Mench January 28, 2008 17:28 Char Count=

4.3 Region II: Ohmic Polarization 159

Table 4.3 Typical Conductivity/Resistivity Values for Selected Fuel Cell Materials

Component

Typical Bulk

Through-Plane

Conductivity σ

or σ

Typical

Thickness Functional Dependencies

PEFC electrolyte σ

= 10 S/m (hydrated) 50–200 µm Temperature, water content

SOFC electrolyte σ

= 1–10 S/m

(>800

◦

10–300 µm Temperature, dopants

(conductivity through oxygen

vacancies)

AFC electrolyte σ

on order of 1–100

S/m at operating

temperature

0.5–2.0 mm Ion concentration, temperature,

charge number on ion, dielectric

constant of solution, mobility,

viscosity, degree of ion

dissociation, other liquids

MCFC electrolyte σ

on order of 1–100

S/m at operating

temperature

0.5–2.0 mm See AFC electrolyte

PAFC electrolyte σ

on order of 1–100

S/m at operating

temperature

0.5–2.0 mm See AFC electrolyte

PEFC bipolar plate

(graphite)

= 5000–20,000 S/m 2–4 mm each Oxide ﬁlm (corrosion), materials,

coatings

PEFC gas diffusion

layer (GDL)

= 10,000 S/m

(much less in plane)

100–300 µm Approximately constant

PEFC catalyst layer ∼1–5 S/m 5–30 µm Morphology, Naﬁon and carbon

loading, age

Contact resistances

for cell

Very low if built well;

resistance ∼30

m·cm

Not available,

use area as

contact area

Compression, pressure,

temperature, age (corrosion),

number of cycles, and others,

current collector total landing

area

Total cell resistance

(based on active

cell area)

Total resistance < 100

m·cm

Not available,

use cell

superﬁcial

active area

See above

2. Material Thickness The ohmic losses are directly proportional to the distance

traveled by the current. In addition to a compact design, this is the reason the

electrolyte and other components are manufactured to be as thin as other constraints

will allow.

Example 4.6 Estimate Total Fuel Cell Resistance Given the experimental polarization

data for a SOFC at 700

◦

C from [13], estimate the ionic resistance of the electrolyte. Is this

a maximum or a minimum value for the actual ohmic resistance of the electrolyte?

SOLUTION To estimate the ohmic resistance of the electrolyte under these conditions,

we can take the slope of the main linear region of the polarization curve. In doing so, we

are assuming that the activation and concentration polarization are minor. Although not