Майсеня Л.И. Математика в примерах и задачах. Часть 4
Подождите немного. Документ загружается.

138
(())()
fgtgtdt
α
+∞
′
∫
вытекает сходимость другого интеграла, и
справедлива формула замены переменной
()(())().
a
fxdxfgtgtdt
α
+∞+∞
′
=
∫∫
(21.7)
Признаки сходимости несобственных интегралов
первого рода от неотрицательных функций
1. Признак сравнения
Пусть функции f (x) и g(x) определены на промежутке
[
)
;,
a
+∞
интегрируемые на любом конечном промежутке [a; b],
и для них выполняется неравенство
0()(),
fxgx
≤≤
[
)
;.
xa
∈+∞
Тогда:
1) из сходимости интеграла
()
a
gxdx
+∞
∫
вытекает сходимость
интеграла
();
a
fxdx
+∞
∫
2) из расходимости интеграла
()
a
fxdx
+∞
∫
вытекает расходи-
мость интеграла
().
a
gxdx
+∞
∫
2. Предельный признак сравнения
Пусть на промежутке
[
)
;a
+∞
определены две положитель-
ные функции f (x) и g(x), интегрируемые на любом конечном
промежутке [a; b]. Если существует конечный предел
()
lim0,
()
x
fx
M
gx
→+∞
=>
то несобственные интегралы
()
a
fxdx
+∞
∫
и
()
a
gxdx
+∞
∫
вместе сходятся или вместе расходятся.
139
3. Пусть неотрицательная функция f (x) определена на про-
межутке
[
)
;,
a
+∞
0.
a
>
Если на этом промежутке для нее спра-
ведливо неравенство
()
,
p
c
fx
x
≤ где c, p – определенные посто-
янные величины, причем
1,
p
>
то интеграл
()
a
fxdx
+∞
∫
сходится.
Если справедливо неравенство
()
,
p
c
fx
x
≥ где
1,
p
≤
то инте-
грал
()
a
fxdx
+∞
∫
расходится.
4. Пусть неотрицательная функция f (x) определена на про-
межутке
[
)
;,
a
+∞
0.
a
>
Если при
1
p
>
существует
lim(),
p
x
fxxc
→+∞
=
0,
c
≤<+∞
то интеграл
()
a
fxdx
+∞
∫
сходится. Ес-
ли при
1
p
≤
выполняется
lim(),
p
x
fxxc
→+∞
=
0,
c
<≤+∞
то инте-
грал
()
a
fxdx
+∞
∫
расходится.
Сходимость несобственных интегралов первого рода
от знакопеременных функций
Если
()
a
fxdx
+∞
∫
сходится, то несобственный интеграл
()
a
fxdx
+∞
∫
называется абсолютно сходящимся.
1. Если несобственный интеграл первого рода сходится аб-
солютно, то он сходится.
2. Если интеграл
()
a
fxdx
+∞
∫
абсолютно сходящийся, а функ-
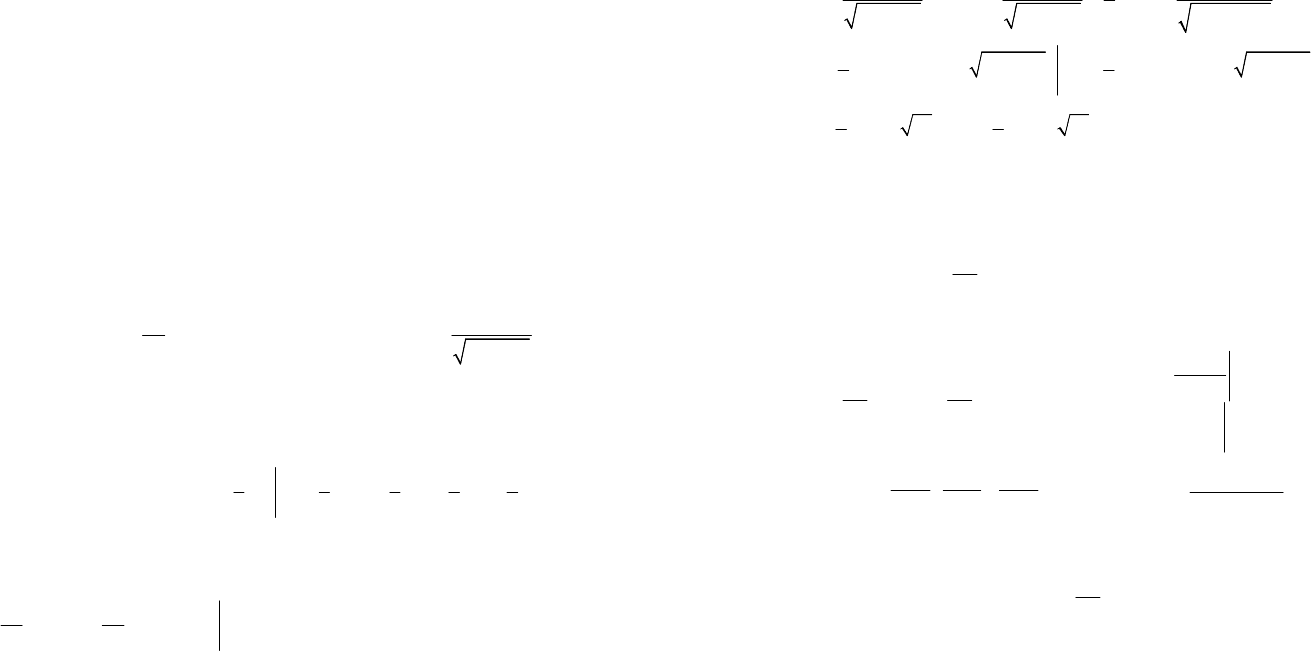
140
ция g(x) ограничена на промежутке
[
)
;,
a
+∞
то интеграл
()()
a
fxgxdx
+∞
∫
также сходится абсолютно.
З а м е ч а н и е 1. Если несобственный интеграл первого рода от
знакопеременной функции не сходится абсолютно, то это еще не озна-
чает, что он расходится. Для исследования на сходимость данного ин-
теграла необходимо использовать другие признаки, в частности, при-
знак Абеля-Дирихле: пусть функции f (x) и g(x) определены и непре-
рывны на промежутке
[
)
;,
a
+∞
причем функция g(x) монотонно стре-
мится к нулю при
,
x
→+∞
имеет непрерывную производную
(),
gx
′
а
функция f(x) имеет ограниченную первообразную F(x) при
[
)
;.
xa
∈+∞
Тогда интеграл
()()
a
fxgxdx
+∞
∫
сходится.
З а м е ч а н и е 2. Всюду далее будем исследовать интегралы на
сходимость в смысле определений (21.1), (21.3) и (21.4). В смысле
главного значения необходимо исследовать только те примеры, в кото-
рых это требуется по условию.
Пример 1. Исследовать на сходимость интегралы:
1)
0
3
;
x
edx
−∞
∫
2)
2
1
;
dx
x
+∞
∫
3)
0
sin;
xdx
+∞
∫
4)
4
1
.
161
xdx
x
+∞
−
∫
В случае сходимости вычислить их.
Решение. 1) По определению (21.3) несобственного интеграла
имеем:
00
0
3333
11111
limlimlim0,
33333
xxxa
aaa
a
a
edxedxee
→−∞→−∞→−∞
−∞
===−=−=
∫∫
значит, интеграл сходится.
2) По определению (21.1) несобственного интеграла имеем:
1
11
limlimlnlimlnln10.
b
b
bbb
dxdx
xb
xx
+∞
→+∞→+∞→+∞
===−=+∞−=+∞
∫∫
Интеграл расходится, так как первообразная
()ln
Fxx
= является
бесконечно большой функцией на бесконечности.
141
3) Интеграл
0
sin
xdx
+∞
∫
расходится, так как функция
0
()sincos1,
b
bxdxb
Φ==−
∫
0,
b
>
не стремится ни к какому пределу при
.
b
→+∞
4) Вычисляем:
2
4422
111
1(4)
limlim
8
161161(4)1
bb
bb
xdxxdxdx
xxx
+∞
→+∞→+∞
===
−−−
∫∫∫
(
)
(
)
2422
1
11
limln4161limln4161
88
bb
xxbb
+∞
→+∞→+∞
=+−=+−−
11
ln(415)ln(415).
88
−+=∞−+=∞
Интеграл расходится.
Пример 2. Исследовать, при каких значениях p сходится несобст-
венный интеграл
,0.
p
a
dx
a
x
+∞
>
∫
Решение. По определению (21.1) имеем:
1
lim,åñëè 1
1
limlim
limln||,åñëè 1
p
b
bb
b
p
a
pp
b
bb
aaa
b
a
x
p
dxdx
p
xdx
xx
xp
−+
+∞
→+∞
−
→+∞→+∞
→+∞
≠−
−+
====
=
∫∫∫
( )
()
11
1
111
1
lim,åñëè 1
, åñëè 1;
1
1
limlnln,åñëè 1
, åñëè 1.
pp
p
b
b
p
p
p
ba
pa
bap
p
−−
−
→+∞
→+∞
−≠−
>
−
==
−
−=
∞≤
Следовательно, интеграл
( )
0
p
a
dx
a
x
+∞
>
∫
сходится, если
1,
p
>
и
расходится, если
1.
p
≤
Пример 3. Вычислить несобственный интеграл первого рода:
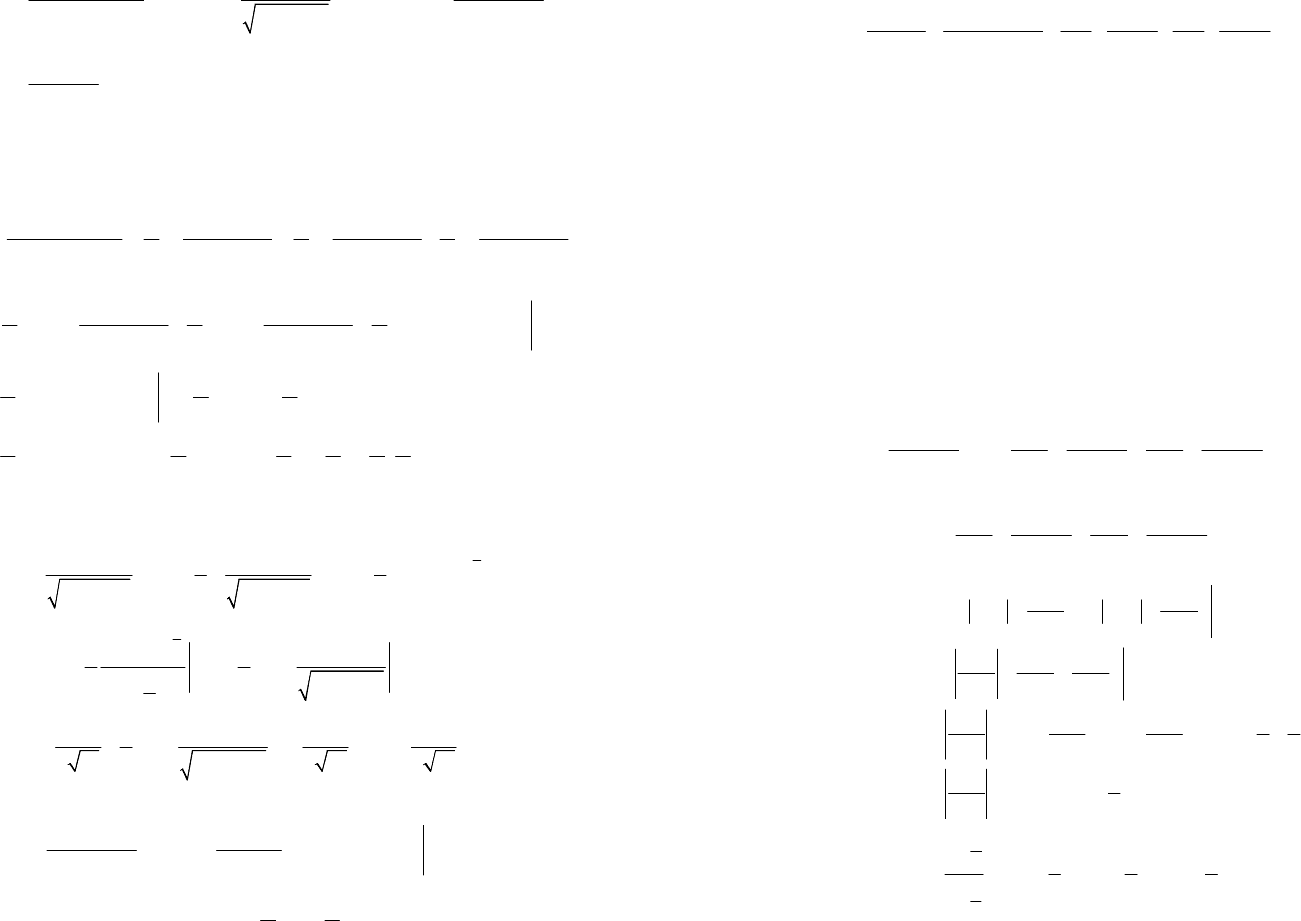
142
1)
2
;
(45)
dx
xxπ
+∞
−∞
++
∫
2)
0
27
5
;
(9)
xdx
x
−∞
+
∫
3)
2
1
;
(1ln)
dx
xx
+∞
+
∫
4)
22
3
4
;
(1)
dx
x
+∞
−
∫
5)
0
.
x
xedx
−∞
∫
Решение. 1) Выделим в знаменателе подынтегрального выраже-
ния полный квадрат и представим заданный интеграл в виде суммы
двух интегралов:
0
2222
0
111
(45)(2)1(2)1(2)1
dxdxdxdx
xxxxx
πππ
π
+∞∞+∞
−∞−∞−∞
==+=
++++++++
∫∫∫∫
0
0
22
0
0
111
limlimlimarctg(2)
(2)1(2)1
111
limarctg(2)arctg2limarctg(2)
1111
limarctg(2)arctg22.
22
b
aba
à
a
b
ba
b
dxdx
x
xx
xa
b
πππ
πππ
ππ
ππππ
→−∞→+∞→−∞
→+∞→−∞
→+∞
=+=++
++++
++=−++
++−=−⋅−+⋅=
∫∫
2) Используем метод поднесения под знак дифференциала. Для это-
го, выделив производную квадратного трехчлена в числителе, получим:
000
7
22
5
2727
55
121
limlim(9)(9)
22
(9)(9)
aa
aa
xdxxdx
xdx
xx
−
→−∞→−∞
−∞
==++=
++
∫∫∫
2
2
5
00
22
5
1(9)51
limlim
2
24
(9)
5
aa
aa
x
x
−
→−∞→−∞
+
==−=
+
−
555
22
5
55155
lim0.
4
481481481
(9)
a
a
→−∞
=−+=−+=−
+
3) Вычисляем:
22
1
11
(ln)
limlimarctgln
(1ln)1ln
b
b
bb
dxdx
x
xxx
+∞
→+∞→+∞
===
++
∫∫
limarctglnarctgln10.
22
b
b
ππ
→+∞
=−=−=
143
4) Представим подынтегральную функцию в виде суммы про-
стейших дробей:
222222
44
.
11
(1)(1)(1)(1)(1)
ABCD
xx
xxxxx
==+++
−+
−−+−+
Далее приводим дроби к общему знаменателю и приравниваем
числители:
2222
4(1)(1)(1)(1)(1)(1).
AxxBxCxxDx=−++++−++− (21.8)
Неизвестные коэффициенты найдем с помощью метода частных
значений:
1,44,1.
xBB
===
1,44,1.
xDD
=−==
Вычислим производную от обеих частей равенства (21.8):
22
0(1)2(1)(1)2(1)(1)
AxAxxBxCx
=++−++++−+
2(1)(1)2(1).
CxxDx
+−++−
Тогда для
1
x
=
получаем:
440,,1.
ABABA
+==−=−
Для
1
x
=−
имеем:
440,,1.
CDCDC
−===
В итоге получаем:
2222
33
22
3
41111
11
(1)(1)(1)
1111
lim
11
(1)(1)
b
b
dx
dx
xx
xxx
dx
xx
xx
+∞+∞
→+∞
−
=+++=
−+
−−+
−
=+++=
−+
−+
∫∫
∫
3
3
1
1
11
limln1ln1
11
111
limln
111
11111
limlnlimlimln2
11124
13
lnlim00ln2
14
1
333
lnlimln2ln1ln2l
444
1
b
b
b
b
bbb
b
b
b
b
xx
xx
x
xxx
b
bbb
b
b
→+∞
→+∞
→+∞→+∞→+∞
→+∞
→+∞
=−−−++−=
−+
+
=−−=
−−+
+
=−−−−−=
−−+
+
=−−−+=
−
+
=−+=+−=−
−
n2.
5) Применим формулу интегрирования по частям:

144
00
00
,,
lim
,
limlim0limlim
lim1limlim1.
x
xx
x
a
a
xxax
aaaa
aa
aaa
aaa
uxdvedx
xedxxedx
dudxve
xeedxaee
aeeae
→−∞
−∞
→−∞→−∞→−∞→−∞
→−∞→−∞→−∞
==
===
==
=−=−−=
=−−+=−−
∫∫
∫
Для вычисления предела используем правило Лопиталя (по пере-
менной a):
()1
lim1lim1lim1lim1011.
()
a
aaa
aaaa
aa
ae
eee
−−−
→−∞→−∞→−∞→−∞
′
−−=−−=−−=−−=−=
′
−
Пример 4. Найти главное значение несобственного интеграла:
1)
2
;
16
dx
x
+∞
−∞
+
∫
2)
2
1
.
1
x
dx
x
+∞
−∞
+
+
∫
Решение. 1) Найдем главное значение данного интеграла по опре-
делению (21.5):
V.p.
22
1
limlimarctg
44
1616
a
a
aa
a
a
dxdxx
xx
+∞
→+∞→+∞
−
−∞−
===
++
∫∫
11
limarctgarctglimarctgarctg
444444
aa
aaaa
→+∞→+∞
=−−=+=
11
lim2arctg2.
44424
a
a
ππ
→+∞
==⋅⋅=
Заметим, что вычисление интеграла по формуле (21.4) также дает
4
π
(просьба убедиться самостоятельно), т. е. он сходится и в обычном
смысле.
2) Найдем главное значение данного интеграла по определе-
нию (21.5):
2222
2
2
1112
V.p.limlim
2
1111
1(1)
limarctg
2
1
aaa
aa
aaa
a
a
a
a
a
xxdxxdx
dxdx
xxxx
dx
x
x
+∞
→+∞→+∞
−∞−−−
→+∞
−
−
++
==+=
++++
+
=+=
+
∫∫∫∫
∫
145
2
1
limarctgarctg()ln(1)
2
a
a
a
aax
→+∞
−
=−−++=
22
11
lim2arctgln(1)ln(1)lim2arctg2.
222
aa
aaaa
π
π
→+∞→+∞
=++−+==⋅=
Можно убедиться, что интеграл
2
1
1
x
dx
x
+∞
−∞
+
+
∫
является расходящимся в
обычном смысле.
Пример 5. Исследовать интеграл на сходимость, используя при-
знак сравнения:
1)
2
1
;
dx
xx
+∞
+
∫
2)
4
3
1
3
.
x
dx
x
+∞
+
∫
Решение. 1) При
)
1;,
x
∈+∞
функция
2
1
0,
xx
>
+
причем
22
11
().
gx
xxx
<=
+
Интеграл
2
1
dx
x
+∞
∫
сходится, так как
22
1
11
11
limlimlim11.
b
b
bbb
dxdx
xb
xx
+∞
→+∞→+∞→+∞
==−=−+=
∫∫
Поэтому, согласно признаку сравнения, интеграл
2
1
dx
xx
+∞
+
∫
сходится.
2) Функция
4
3
3
0
x
x
+
>
при
)
1;,
x
∈+∞
причем
()
44
33
31
.
x
gx
xx
+
>=
Интеграл
∫
+∞
1
4
3
x
dx
расходится, так как
1
3
4
4
4
44
33
11
111
1
4
limlimlim4lim4.
bb
bb
bbbb
dxdxx
xdxx
xx
−
+∞
→+∞→+∞→+∞→+∞
=====∞−=∞
∫∫∫
Поэтому, согласно признаку сравнения, интеграл
4
3
1
3
x
dx
x
+∞
+
∫
расходится.
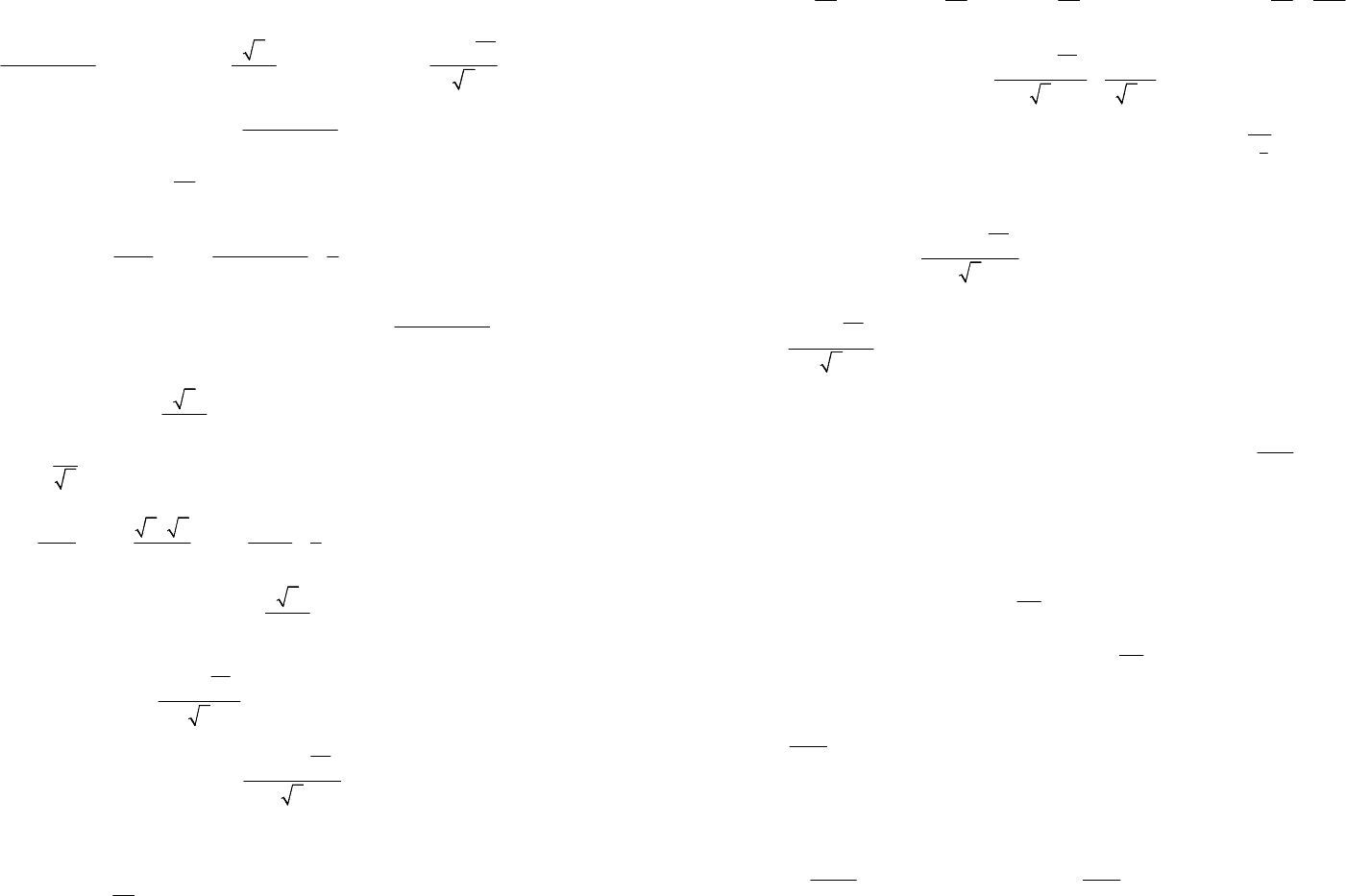
146
Пример 6. Исследовать на сходимость несобственные интегралы
по предельному признаку сравнения:
1)
7
1
;
722
dx
xx
+∞
++
∫
2)
1
;
21
x
dx
x
+∞
−
∫
3)
2
1
1
lncos
.
x
dx
x
+∞
∫
Решение. 1) Функция
()
7
1
0
722
fx
xx
=>
++
при
)
1;.
x
∈+∞
Рас-
смотрим функцию
()
7
1
,
gx
x
= интеграл от которой сходится (пример 2,
с. 141 данного пособия).
Найдем
7
7
()1
limlim0.
()2
722
xx
fxx
gx
xx
→+∞→+∞
==≠
++
Поэтому, согласно
предельному признаку сравнения заключаем, что
7
1
722
dx
xx
+∞
++
∫
также
сходится.
2) Функция
()0
21
x
fx
x
=>
−
при
)
1;.
x
∈+∞
Рассмотрим функ-
цию
()
1
,
gx
x
= интеграл от которой расходится (пример 2, с. 141).
Находим:
()1
limlimlim0.
()21212
xxx
fxxxx
gxxx
→+∞→+∞→+∞
⋅
===≠
−−
Поэтому, согласно
предельному признаку сравнения,
1
21
x
dx
x
+∞
−
∫
расходится.
3) Функция
()
2
1
lncos
0
x
fx
x
=<
при
[
)
1;.
x
∈+∞
Поэтому иссле-
дуем на сходимость интеграл
2
1
1
lncos
,
x
dx
x
+∞
−
∫
который будет схо-
диться или расходиться одновременно с заданным интегралом. Ис-
пользуем эквивалентность бесконечно малых функций:
ln(1)~,
xx
+
0,
x
→
2
1cos~,
2
x
x−
0.
x
→
Сделаем следующие преобразования:
147
222
111
lncosln1cos1~cos1,
xxx
=+−−
;
x
→+∞
24
11
1cos~,
2
xx
−
.
x
→+∞
Поэтому имеем
2
4
1
lncos
1
~,
2
x
xxx
−
.
x
→+∞
Так как из-
вестно, что несобственный интеграл от функции
()
9
2
1
gx
x
= сходится
на промежутке
[
)
1;
+∞
(пример 2, с. 141 данного пособия), то сходится
также интеграл
2
1
1
lncos
,
x
dx
x
+∞
−
∫
а вместе с ним и заданный интеграл
2
1
1
lncos
.
x
dx
x
+∞
∫
Пример 7. Исследовать на сходимость интеграл
1
sin
,
p
x
dx
x
+∞
∫
где
0.
p
>
Решение. Используем признак Абеля-Дирихле. Функция
()sin
fxx
= имеет ограниченную первообразную
()cos,
Fxx
=−
[
)
1;,
x
∈+∞
функция
()
1
p
gx
x
= монотонно убывает и имеет непре-
рывную производную. Кроме того,
1
lim0.
p
x
x
→+∞
=
Таким образом, все
условия признака Абеля-Дирихле выполняются, а значит интеграл
1
sin
p
x
dx
x
+∞
∫
сходится.
Пример 8. Исследовать интеграл на абсолютную сходимость:
1)
2
0
sin3
;
1
x
dx
x
+∞
+
∫
2)
1
sin
.
x
dx
x
+∞
∫
148
Решение. 1) Так как
sin31
x
≤
для любого
[
)
0;,
x
∈+∞
то
22
0
00
sin3
limarctglimarctg.
2
11
a
aa
x
dx
dxxa
xx
π
+∞+∞
→+∞→+∞
≤===
++
∫∫
Следовательно, интеграл
2
0
sin3
1
x
dx
x
+∞
+
∫
сходится абсолютно.
2) Интеграл
1
sin
x
dx
x
+∞
∫
сходится в силу признака Абеля-Дирихле
(см. пример 7, с. 147). Рассмотрим интеграл
1
sin
.
x
dx
x
+∞
∫
Так как
2
1cos2
sinsin,
2
x
xx
−
≥= то для любого
1
b
>
имеем:
1111
sin
1cos211cos2
.
222
bbbb
x
xdxx
dxdxdx
xxxx
−
≥=−
∫∫∫∫
(21.9)
Осуществив предельный переход в неравенстве (21.9) при
,
b
→+∞
получаем:
111
sin
11cos2
.
22
x
dxx
dxdx
xxx
+∞+∞+∞
≥−
∫∫∫
Интеграл
1
cos2
x
dx
x
+∞
∫
сходится в силу признака Абеля-Дирихле, а
интеграл
1
dx
x
+∞
∫
расходится (пример 2, с. 141 данного пособия). Прихо-
дим к выводу, что в результате предельного перехода в неравенстве
(21.9) получим
1
sin
.
x
dx
x
+∞
=+∞
∫
Таким образом, интеграл
1
sin
x
dx
x
+∞
∫
сходится, однако он не сходится абсолютно.
149
Задания
I уровень
1.1. Вычислите несобственный интеграл или установите его
расходимость:
1)
2
1
;
dx
x
+∞
∫
2)
2
;
dx
x
+∞
∫
3)
0
2
;
1
dx
x
−∞
+
∫
4)
0
5
;
x
edx
−∞
∫
5)
5
0
3;
x
dx
+∞
−
∫
6)
2
.
9
dx
x
+∞
−∞
+
∫
II уровень
2.1. Вычислите несобственный интеграл или установите его
расходимость:
1)
3
4
0
;
161
xdx
x
+∞
+
∫
2)
1
cos;
xdx
+∞
∫
3)
4
1
;
41
xdx
x
+∞
−
∫
4)
2
1
;
45
dx
xx
+∞
−
++
∫
5)
4
1
;
251
xdx
x
+∞
−
∫
6)
2
0
arctg2
2
;
14
x
dx
x
π
+∞
+
∫
7)
2
34
3
0
;
(5)
xdx
x
+∞
+
∫
8)
2
;
22
dx
xx
+∞
−∞
−+
∫
9)
22
1
3
;
(19)arctg3
dx
xx
∞
+
∫
10)
2
1
;
45
xdx
xx
+∞
−
++
∫
11)
2
0
arctg2
;
14
x
dx
x
∞
+
∫
12)
2
1
2
16
;
(445)
dx
xxπ
+∞
++
∫
13)
0
23
;
(9)
xdx
x
−∞
+
∫
14)
2
1
;
(1)
dx
xx
+∞
+
∫
15)
0
2
32
;
11
xx
dx
xx
−∞
−
−+
∫
16)
2
1
;
(1ln)
dx
xx
+∞
+
∫
17)
1
2
;
4
dx
xx
−∞
−
∫
18)
2
3
;
32
dx
xx
+∞
−+
∫
19)
2
2
;
(ln1)
e
dx
xx
+∞
−
∫
20)
2
0
3
;
4
x
dx
x
+∞
−
+
∫
21)
24
3
0
(2)
;
(41)
xdx
xx
+∞
+
++
∫
150
22)
2
2
11
sin;
dx
x
x
π
+∞
∫
23)
3
0
;
1
dx
x
+∞
+
∫
24)
2
1
2
.
1
dx
xx
+∞
+
∫
2.2. Исследуйте на сходимость несобственный интеграл
первого рода:
1)
1
arctg
;
x
dx
x
+∞
∫
2)
3
2
3sin
;
x
dx
x
π
+∞
+
∫
3)
4
32
1
32
;
2
xx
dx
xx
+∞
++
++
∫
4)
0
cos;
x
exdx
+∞
−
∫
5)
2
0
sin4;
x
exdx
+∞
−
∫
6)
3
24
3
;
1
dx
xx
+∞
−
++
∫
7)
7
0
;
1
xdx
x
+∞
+
∫
8)
3
1
1
tg
;
1
x
dx
xx
+∞
+
∫
9)
1
1
1arcsin
;
1
x
dx
xx
∞
+
+
∫
10)
2
1
;
sin
dx
xx
+∞
+
∫
11)
2
3
cos
;
1
x
dx
x
π
+∞
+
∫
12)
2
3
1
1
.
2
xx
dx
xx
+∞
++
++
∫
2.3. Исследуйте на абсолютную сходимость несобственный
интеграл первого рода:
1)
1
sin
;
x
dx
x
+∞
∫
2)
2
0
cos
;
4
x
dx
x
+∞
+
∫
3)
2
1
cos3
;
x
dx
x
+∞
∫
4)
0
arcsin
.
x
dx
x
+∞
∫
III уровень
3.1. Используя формулу интегрирования по частям, вычис-
лите несобственный интеграл или установите его расходимость:
1)
0
;
x
xedx
+∞
−
∫
2)
0
2;
x
xdx
−∞
∫
3)
0
cos;
x
exdx
+∞
−
∫
151
4)
0
sin2;
x
exdx
+∞
−
∫
5)
0
sin;
xxdx
+∞
∫
6)
3
0
.
(1)
xdx
x
+∞
+
∫
3.2. Найдите главное значение несобственного интеграла и
определите, сходится ли интеграл в обычном смысле:
1)
arctg;
xdx
+∞
−∞
∫
2)
2
;
9
dx
x
+∞
−∞
+
∫
3)
2
2
arctg
;
1
x
dx
x
+∞
−∞
+
∫
4)
sin;
xdx
+∞
−∞
∫
5)
2
;
1
x
x
edx
e
+∞
−∞
+
∫
6)
2
21
.
1
x
dx
x
+∞
−∞
+
+
∫
3.3. Докажите сходимость несобственных интегралов Фре-
неля
2
0
sin
xdx
+∞
∫
и
2
0
cos.
xdx
+∞
∫
У к а з а н и е. Выполните замену
.
xt
=
3.4. Исследуйте интеграл на сходимость:
1)
2
4
0
1
1
x
dx
x
+∞
+
+
∫
(у к а з а н и е:
1
);
tx
x
=−
2)
0
1
sin
dx
x
+∞
∫
(у к а з а н и е:
1
);
t
x
=
3)
2
lnlnln
e
dx
xxx
+∞
∫
(у к а з а н и е:
ln);
tx
=
4)
2
1
xx
xedx
+∞
−
∫
(у к а з а н и е: сравните
() ()
2
2
ln
1
);
x
x
x
x
gxecfxe
−−
−
==
5)
2
0
x
edx
+∞
−
∫
(у к а з а н и е: сравните
2
x
e
−
и
21
).
x
e
−+
152
21.2. Несобственный интеграл второго рода
Пусть функция f (x) является непрерывной на промежутке
[a; b) и неограниченной в окрестности точки
,
xb
=
т. е.
0
lim().
xb
fx
→−
=∞
Тогда точка b называется особой точкой и гово-
рят, что функция f (x) имеет особенность в точке b. Для любо-
го
0
ε
>
()
ba
ε
<−
функция f (x) интегрируема на отрезке
[
]
;,
ab
ε
− т. е. существует интеграл
()().
b
a
Ifxdx
ε
ε
−
=
∫
(21.10)
Результат вычисления предела функции
()
I
ε
при
0
ε
→+
называется несобственным интегралом второго рода:
00
lim()lim()().
bb
aa
Ifxdxfxdx
ε
εε
ε
−
→+→+
==
∫∫
(21.11)
Несобственный интеграл второго рода (21.11) называется
сходящимся, если предел (21.11) существует. Если функция
()
I
ε
является бесконечно большой, то несобственный интеграл
считают равным бесконечности. Если предел (21.11) не сущест-
вует, то интеграл не принимает никакого значения. В последних
двух случаях несобственный интеграл второго рода называется
расходящимся.
Если для функции f (x), определенной на полуинтервале
[a, b), известна ее первообразная F(x), то для вычисления инте-
грала (21.11) используется формула Ньютона-Лейбница
0
()lim()().
b
a
fxdxFbFa
ε
ε
→+
=−−
∫
(21.12)
Формула интегрирования по частям для несобственного
интеграла второго рода
Если функции u(x) и v(x) имеют непрерывные производные
на промежутке [a, b), а также существует
0
lim()(),
ubvb
ε
εε
→+
−−
то
из сходимости одного из интегралов
()(),
b
a
uxvxdx
′
∫
()()
b
a
uxvxdx
′
∫
153
вытекает сходимость другого, и справедлива формула
0
()()lim()()()()()().
bb
aa
uxvxdxubvbuavavxuxdx
ε
εε
→+
′′
=−−−−
∫∫
Формула замены переменной в несобственном интеграле
второго рода
Если функция f (x) непрерывна на промежутке [a, b), функция
()
xgt
=
определена на полуинтервале
[
)
;,
αβ
,
αβ
−∞<<<+∞
и имеет на нем непрерывную производную, причем
(),
ga
α
=
lim(),
t
gtb
β→
=
то справедлива формула
()(())(),
b
a
fxdxfgtgtdt
β
α
′
=
∫∫
при этом интегралы в ней оба сходятся или оба расходятся.
Аналогично определяется несобственный интеграл второго
рода, если
xa
=
– особая точка функции f (x):
0
()lim().
bb
aa
fxdxfxdx
ε
ε
→+
+
=
∫∫
(21.13)
Если особая точка
c
x
=
функции f (x) является внутренней
точкой отрезка [a; b] (функция f (x) имеет в этой точке разрыв
второго рода), то несобственный интеграл второго рода функции
f (x) по отрезку [a; b] определяется равенством:
1
12
2
00
()lim()lim().
c
bb
aac
fxdxfxdxfxdx
ε
εε
ε
−
→+→+
+
=+
∫∫∫
(21.14)
З а м е ч а н и е 1. Следует различать сходимость, определенную
равенством (21.14), и сходимость в смысле главного значения (21.15),
которая определяется следующим образом: пусть функция f (x) опреде-
лена на отрезке [a; b] с особой точкой
(;)
cab
∈ и интегрируема на
любом отрезке, принадлежащем полуинтервалам [a; c) и (c; b]. Если
для
0
ε
>
такого, что
{
}
min,
cabc
ε
<−−
существует
0
lim()()V.p.(),
cbb
aca
fxdxfxdxfxdx
ε
ε
ε
−
→+
+
+=
∫∫∫
(21.15)
то он называется главным значением несобственного интеграла
второго рода, а функция f (x) – интегрируемой по Коши.

154
Всюду далее будем рассматривать сходимость, определен-
ную равенством (21.14).
Признаки сходимости несобственных интегралов
второго рода от неотрицательных функций
1. Признак сравнения
Пусть функции f (x) и g(x) определены на промежутке [a; b)
и для них выполняется неравенство
0()(),
fxgx
≤≤
[
)
;.
xab
∈
Тогда из сходимости интеграла
()
b
a
gxdx
∫
следует сходимость
интеграла
(),
b
a
fxdx
∫
а из расходимости интеграла
()
b
a
fxdx
∫
вы-
текает расходимость интеграла
().
b
a
gxdx
∫
2. Предельный признак сравнения
Пусть на промежутке [a; b) определены положительные
функции f (x) и g(x), для которых
()
lim,
()
xb
fx
M
gx
→
=
0.
M
>
Тогда
оба интеграла
()
b
a
fxdx
∫
и
()
b
a
gxdx
∫
вместе сходятся или оба
вместе расходятся.
3. Пусть неотрицательная функция f (x) определена на про-
межутке [a; b) и для x, близких к b, удовлетворяет условию
()
,
()
p
A
fx
bx
≤
−
0.
A
>
Тогда при
1
p
<
несобственный интеграл
()
b
a
fxdx
∫
сходится. Если для x, близких к b, выполняется нера-
венство
()
( )
p
A
fx
bx
≥
−
,
0,
A
>
тогда при
1
p
≥
интеграл от этой
функции на промежутке [a; b) расходится.
155
Сходимость интегралов второго рода
от знакопеременных функций
Если интеграл
()
b
a
fxdx
∫
сходится, то несобственный инте-
грал
()
b
a
fxdx
∫
называется абсолютно сходящимся.
1. Если несобственный интеграл второго рода сходится аб-
солютно, то он сходится.
2. Если интеграл
()
b
a
fxdx
∫
абсолютно сходящийся, а функ-
ция g(x) ограничена на промежутке [a; b), то интеграл
()()
b
a
fxgxdx
∫
также сходится абсолютно.
З а м е ч а н и е 2. Если несобственный интеграл второго рода от
знакопеременной функции не сходится абсолютно, то это еще не озна-
чает, что он расходится. Для исследования на сходимость данного ин-
теграла необходимо использовать другие признаки.
Пример 1. Исследовать интеграл
1
0
,
p
dx
x
∫
,
pconst
=
0,
p
>
на схо-
димость и в случае сходимости вычислить его.
Решение. Подынтегральная функция неограничена в окрестности
точки
0.
x
=
Обозначим
()
1
,
p
dx
I
x
ε
ε =
∫
где
01.
ε
<<
Вычислим этот интеграл
1
1
1
(1), åñëè 1,
1
ln,åñëè 1.
p
p
dx
p
p
x
p
ε
ε
ε
−
−≠
=
−
−=
∫
Заключаем, что конечный предел
0
lim()
I
ε
ε
→+
существует при
1
p
<
и не существует при
1.
p
≥
Мы получили следующий результат:
156
1
0
1
, åñëè 1 (ñõîäèòñÿ),
1
, åñëè 1 (ðàñõîäèòñÿ).
p
dx
p
p
x
p
<
=
−
+∞≥
∫
(21.16)
Аналогично можно показать, что для функций
1
()
p
y
bx
=
−
,
[
)
;,
xab
∈ и
1
,
()
p
y
xa
=
−
(
]
;,
xab
∈ интегралы
()
b
p
a
dx
bx
−
∫
и
()
b
p
a
dx
xa
−
∫
сходятся при
1
p
<
и расходятся при
1.
p
≥
Пример 2. Вычислить несобственный интеграл или установить
его расходимость:
1)
3
2
3
1
;
(3)
dx
x
−
∫
2)
1
1
2
ln(21)
;
21
x
dx
x
−
−
∫
3)
3
1
;
(1)(3)
dx
xx
−−
∫
4)
2
3
5
2
0
sin
.
cos
xdx
x
π
∫
Решение. 1) Подынтегральная функция имеет особенность в точке
3
x
=
– правом конце промежутка интегрирования. Для вычисления
интеграла используем формулы (21.11) и (21.12):
2
3
1
3
333
22
00
33
111
33
3333
000
11
1
3
limlim(3)(3)
(3)(3)
(3)
lim3lim33(lim2)32.
dxdx
xdx
xx
x
x
εε
εε
εε
εεε
ε
−
−−
→+→+
−−
→+→+→+
==−−−=
−−
−
=−=−−=−−=
∫∫∫
2) Подынтегральная функция имеет особенность в точке
1
2
x
=
– в
левом конце промежутка. Согласно формуле (21.13) и формуле Нью-
тона-Лейбница, имеем:
11
1
2
1
00
2
11
22
ln(21)11ln(21)
limln(21)ln(21)lim
21222
xx
dxxdx
x
εε
ε
ε
→+→+
+
+
−−
=−−==
−
∫∫
22
00
11
lim(ln1ln(121))limln2.
44
εε
εε
→→
=−+−=−=+∞
157
Интеграл расходится.
3) Подынтегральная функция имеет две особые точки:
1,
x
=
3
x
=
–
концы промежутка интегрирования.
Тогда
2
121
11
2
212
1
323
112
3
22
222
000
121
3
2
2
000
1
2
(1)(3)(1)(3)(1)(3)
(2)
limlimlim
43431(2)
(2)
limlimarcsin(2)limarcsin(
1(2)
dxdxdx
xxxxxx
dxdxdx
xxxxx
dx
xx
x
ε
εεε
εε
ε
εεε
ε
−
→+→+→+
++
−
→+→+→+
+
=+=
−−−−−−
−
=+=+
−+−−+−−−
−
+=−+−
−−
∫∫∫
∫∫∫
∫
()
2
12
3
2
12
00
2)
arcsin0limarcsin(1)limarcsin(1)arcsin0
arcsin1arcsin12arcsin12.
2
ε
εε
εε
π
π
−
→+→+
=
=−−+−−=
=−−+==⋅=
4) Подынтегральная функция имеет особенность во внутренней
точке
2
x
π
=
промежутка интегрирования. Для вычисления интеграла
используем формулу (21.14) и формулу Ньютона-Лейбница. Получим:
( ) ( ) ( ) ( )
1
12
2
1
22
55
12
2
3
5
1
1
2
0
3
2
555
222
00
2
2
32
55
22
00
0
2
2
32
00
0
2
2
0
0
sinsinsin
coscoscos
sinsin
limlim
coscos
limcoscoslimcoscos
cos
lim
3
5
xdxxdxxdx
xxx
xdxxdx
xx
xdxxdx
x
π π
π
ππ
ε
εε
π
ε
ππ
ε
εε
π
ε
π
ε
ε
−−
−
→+→
+
−
→+→+
+
−
→+
=+=
=+=
=−−=
=−
∫∫∫
∫∫
∫∫
3
5
2
2
2
3
0
2
cos
lim
3
5
x
π
ε
π
ε
→+
+
−=
