Майсеня Л.И. Математика в примерах и задачах. Часть 4
Подождите немного. Документ загружается.


197
старшей производной, то дифференциальное уравнение n-го по-
рядка имеет вид:
()(1)
(,,,,...,).
nn
yfxyyyy
−
′′′
= (22.44)
Решением дифференциального уравнения n-го порядка яв-
ляется всякая n раз дифференцируемая функция
(),
yyx
=
кото-
рая обращает данное уравнение в тождество. Задача нахождения
решения
(),
yyx
=
удовлетворяющего начальным условиям
00
(),
yxy
=
(
)
(
)
11
0000
(),...,(),
nn
yxyyxy
−−
′′
==
где
(1)
0000
,,,...,
n
xyyy
−
′
– заданные числа, называется зада-
чей Коши.
Общим решением уравнения (22.43) называется функция
12
(,,,...,),
n
yyxCCC
=
(22.45)
где
12
,,...,
n
CCC
– произвольные постоянные.
Типы уравнений, допускающие понижение порядка
Уравнение вида
(
)
(,)0
n
Fxy
=
(22.46)
или разрешенное относительно n-й производной
(
)
()
n
yfx
= (22.47)
решается последовательным интегрированием n раз.
Уравнение вида
(
)
(
)
(,,...,)0,
kn
Fxyy
=
(22.48)
не содержащее явно искомой функции y и первых (
1
k
−
)-х ее
производных,
,
k
∈
N
решают с помощью замены
(
)
,
k
zy
= где
().
zzx
=
Таким образом, порядок исходного уравнения (22.48)
понижается на k единиц.
Приходят к уравнению
(
)
(,,...,)0.
nk
Fxzz
−
=
Полученное уравнение решают далее в зависимости от его
типа.
Уравнение вида
(
)
(,,...,)0,
n
Fyyy
′
=
(22.49)
не содержащее явно независимой переменной x, решают с по-
мощью замены
,
yz
′
=
где
(),
zzy
=
().
yyx
=
198
Этой заменой порядок исходного уравнения понижается на
единицу, поскольку
yxy
yzyzz
′′′′′
==
(функцию z(y) дифференци-
ровали по x как сложную). Аналогично выражают
y
′′′
и т. д.
Уравнение вида
(
)
(,,,...,)0
n
Fxyyy
′
=
(22.50)
называется однородным относительно искомой функции y и ее
производных
(
)
,,...,,
n
yyy
′′′
если функция F однородна относи-
тельно
(
)
,,...,,
n
yyy
′
т. е.
(
)
(
)
(,,,...,)(,,,...,),
nn
m
FxyyyFxyyyλλλλ
′′
=
где m – степень однородности,
;
m
∈
N
λ
– произвольное число.
Для решения используется замена
,
y
z
y
′
= где
(),
zzx
=
по-
нижающая порядок исходного уравнения на единицу.
Пример 1. Найти общее решение уравнения:
1)
sin2;
yx
′′′
=− 2)
20;
xyy
′′′
+=
3)
2
2()0;
yyy
′′′
−=
4)
22
()0.
xyyyxy
′′′
−−=
Решение. 1) Заданное уравнение имеет 3-й порядок. Это диффе-
ренциальное уравнение типа (22.47). Проинтегрируем последовательно
три раза:
( )
1
cos2
sin2,
2
x
yxdxC
′′
=−=+
∫
112
cos2sin2
,
24
xx
yCdxCxC
′
=+=++
∫
2
1
1223
sin2cos2
,
482
Cx
xx
yCxCdxCxC
=++=−+++
∫
123
,,
CCC
– произвольные постоянные. Полученная функция
()
yyx
= и есть общее решение исходного уравнения.
2) Это уравнение 2-го порядка, не содержащее явно искомой
функции y, т. е. типа (22.48). Делаем замену
,
yz
′
=
где
().
zzx
= Диф-
ференцируем замену еще раз, получаем
.
yz
′′′
=
Подставляем выраже-
ния
y
′
и
y
′′
в исходное уравнение:
20.
xzz
′
+=
(22.51)

199
Получили уравнение с разделяющимися переменными:
2
,
dzdx
zx
=−
0,
z
≠
0.
x
≠
В результате интегрирования имеем:
1
ln||2ln||ln,
zxC
=−+ отку-
да
2
1
zCx
−
= – общее решение уравнения (22.51).
Возвращаемся к старым переменным:
2
1
yCx
−
′
= – уравнение первого порядка. Интегрируем его:
2
1
.
dyCxdx
−
=
∫∫
Получаем
1
12
yCxC
−
=+
– общее решение исходного уравнения.
3) Это уравнение 2-го порядка, не содержащее явно независимой
переменной x, т. е. типа (22.49). Делаем замену
,
yz
′
=
где
(),
zzy
=
().
yyx
= Дифференцируем замену по x как сложную функцию, полу-
чаем:
.
yx
yzyzz
′′′′′
== Подставляем выражения для
y
′
и
y
′′
в исходное
уравнение:
2
20.
yzzz
′
−=
(22.52)
Уравнение (22.52) – это уравнение с разделяющимися переменны-
ми. Решаем его:
2
2
dz
yzz
dy
= или
2
,
dzdy
zy
=
0,
z
≠
0.
y
≠
Далее интегрируя, имеем:
1
ln2lnln,
zyC
=+ откуда
2
1
zCy
= – общее решение уравнения (22.52).
Возвращаемся к старым переменным, получаем
2
1
yCy
′
= – урав-
нение с разделяющимися переменными. Тогда
2
1
dy
Cy
dx
= или
1
2
.
dy
Cdx
y
=
Интегрируем:
12
1
CxC
y
−=+
или
12
1
y
CxC
=
+
– общее решение исходного диф-
ференциального уравнения.
4) Это уравнение 2-го порядка, однородное относительно
,
yy
′
и
,
y
′′
так как
22222
()(()),
xyyyxyxyyyxyλλλλλ
′′′′′′
−−=−−
200
где
λ
– произвольное число.
Это уравнение типа (22.50). Делаем замену
,
y
z
y
′
= где
(),
zzx
=
отсюда получаем:
.
yzy
′
= (22.53)
Дифференцируем это равенство еще раз:
.
yzyzy
′′′′
=+
С учетом (22.53) получаем:
2
,
yzyzy
′′′
=+
2
().
yyzz
′′′
=+
Подставляем выражения для
y
′
и
y
′′
в исходное уравнение:
222
()()0.
xyyzzyxzy
′
+−−=
Делим его на
2
y
(
)
0:
y ≠
222
()(1)0.
xzzxz
′
+−−=
После упрощения имеем уравнение
2
120.
xzxz
′
−+=
Делим его почленно на
2
x
(
)
0:
x ≠
2
21
.
z
z
x
x
′
+= (22.54)
Получили линейное уравнение 1-го порядка. Решаем его, напри-
мер, методом Бернулли:
,
zuv
=
.
zuvuv
′′′
=+
Тогда (22.54) примет вид:
2
21
,
uv
uvuv
x
x
′′
++= т. е.
2
21
.
v
uvuv
x
x
′′
++=
Полагаем
2
0,
v
v
x
′
+=
откуда
2
.
dvdx
vx
=−
Интегрирование приводит к равенству
ln||2ln||.
vx
=−
Тогда имеем:
2
1
v
x
= – искомая функция v.
Далее имеем:
22
1
,
u
xx
′
= т. е.
,
dudx
= что означает
1
.
uxC
=+
Отсюда
2
1
().
zxCx
−
=+

201
Возвращаемся к старым переменным:
( )
2
1
y
xCx
y
−
′
=+ или
1
2
1
.
Cdy
dx
yx
x
=+
Интегрируем:
1
2
lnlnln,
C
yxC
x
=−+ используя свойства логарифма, получаем:
1
2
ln
C
y
Cxx
−
=
или
1
2
.
C
x
y
e
Cx
−
=
Таким образом,
1
2
C
x
yCxe
−
= – общее решение исходного уравнения.
Пример 2. Найти частное решение уравнения:
1)
20,
yy
′′′
−=
3
(0),
2
y =
(0)1;
y
′
=
2)
2
32(),
yyy
′′′
=
(0)1,
y
=
(0)2;
y
′
=
3)
ln,
IV
yxx
=
(1)1,
y
=
(1)0,
y
′
=
(1)1,
y
′′
=−
(1)0.
y
′′′
=
Решение. 1) Заданное уравнение имеет 2-й порядок. Делаем заме-
ну
,
zy
′
=
().
zzx
= Тогда
,
yz
′′′
=
и заданное уравнение принимает вид:
20.
zz
′
−=
Получили дифференциальное уравнение 1-го порядка с разде-
ляющимися переменными. Решаем его:
2,
dz
dx
z
=
1
ln||2ln
zxC
=+ или
2
1
.
x
zCe
=
Возвращаясь к старой переменной, получим:
2
1
.
x
yCe
′
=
Определим константу
1
C
из начального условия
(0)1.
y
′
=
Тогда
0
1
1
Ce
= или
1
1.
C
=
Таким образом,
2
.
x
ye
′
= Интегрируем и получаем:
2
2
2
.
2
x
x
e
yedxC
==+
∫
Определяем
2
C
из 2-го начального условия:
3
(0),
2
y =
т. е.
2
1.
C
=
Частным решением исходного дифференциального уравнения яв-
ляется функция
2
1.
2
x
e
y
=+
2) Это уравнение 2-го порядка, не содержащее явно переменную x.
Делаем замену
,
yz
′
=
(),
zzy
=
().
yyx
= Тогда
,
yzz
′′′
= и заданное
уравнение примет вид
2
32.
yzzz
′
= Получили уравнение 1-го порядка с
202
разделяющимися переменными. Интегрируем его:
2
,
3
dzdy
zy
= имеем:
1
2
ln||ln||ln
3
zyC
=+ или
2
3
1
.
zCy
=
Возвращаемся к старой переменной:
2
3
1
.
yCy
′
=
Определяем
1
,
C
используя 2-е начальное условие:
1
21,
C
=⋅
отсюда
1
2.
C
=
Получаем
2
3
2
yy
′
= – уравнение 1-го порядка с разделяющимися
переменными. Его решение:
1
3
2
32
yxC
=+
или
( )
3
2
1
2.
27
yxC=+
Определяем константу
2
,
C
используя первое начальное условие:
3
2
1
1,
27
C
= откуда
2
3.
C
=
Тогда частным решением заданного уравнения является функция
( )
3
1
23.
27
yx=+
3) Это дифференциальное уравнение 4-го порядка типа (22.47).
Проинтегрируем его последовательно четыре раза:
22
1
ln
ln.
24
xxx
yxxdxC
′′′
==−+
∫
Определим константу
1
C
из начального условия
(1)0.
y
′′′
=
Тогда
1
1
0
4
С
=−+
или
1
1
.
4
С
=
Интегрируем еще раз:
2233
2
ln1ln5
.
2446364
xxxxxxx
ydxC
′′
=−+=−++
∫
Определяем
2
C
из начального условия
(
)
11:
y
′′
=−
2
51
1
364
С
−=−++
или
2
10
.
9
С =−
Интегрируем далее:
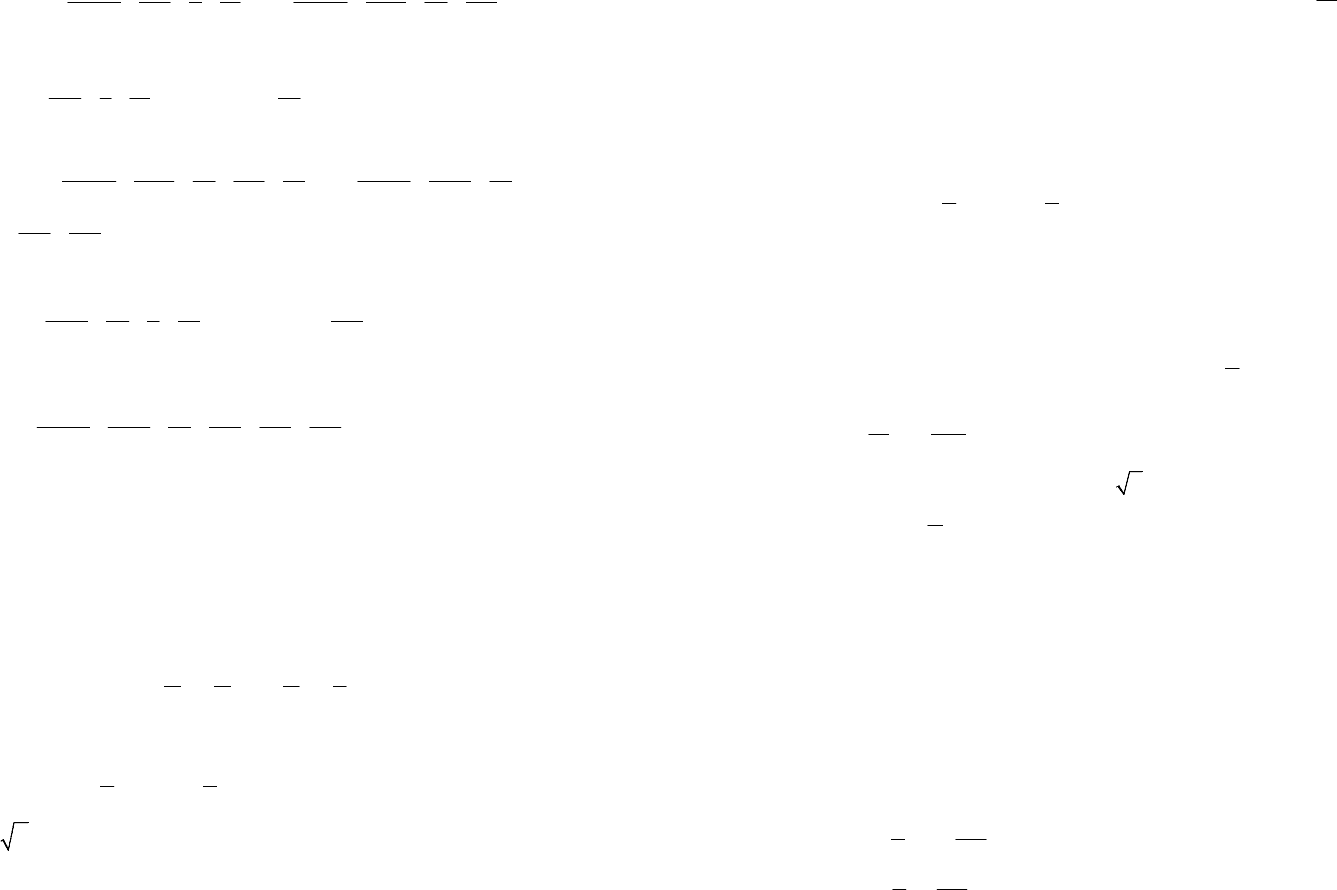
203
33442
3
ln510ln1310
.
636492428889
xxxxxxxxx
ydxC
′
=−+−=−+−+
∫
Из начального условия
(
)
10
y
′
=
находим
3
:
C
3
13110
0
28889
С
=−+−+
или
3
33
.
32
С =
Интегрируем в 4-й раз:
442553
2
4
ln131033ln77
242888932120720024
533
.
932
xxxxxxxxx
ydx
xx
C
=−+−+=−+−
−++
∫
Находим константу
4
C
из начального условия
(
)
11:
y
=
4
771533
1
720024932
С
=−+−++
или
4
114
.
225
С =
Тогда частным решением заданного дифференциального уравне-
ния является функция
5532
ln77533114
.
120720024932225
xxxxxx
y=−+−++
Задания
I уровень
1.1. Решите уравнение:
1)
6;
IV
yx
= 2)
cos32;
yx
′′′
=+
3)
2
();
yy
′′′
= 4)
2
30.
yxy
′′′
+=
1.2. Решите задачу Коши:
1)
3
sincos,
xyx
′′
=
,
22
y
ππ
=
1
;
22
y
π
′
=
2)
2,
y
ye
′′
=
(1)0,
y
=
(1)2;
y
′
=
3)
3
1,
yy
′′
=
1
1,
2
y
=
1
1;
2
y
′
=
4)
2,
yyy
′′′
=
(2)1,
y
=
(2)1.
y
′
=
II уровень
2.1. Решите уравнение:
1)
23
2cossincos;
yxxx
′′
=− 2)
22
()()4;
yy
′′′
+=
204
3)
2
();
yyy
′′′
= 4)
sin;
y
xyyx
x
′
′′′
−=
5)
2
sin;
xyyxx
′′′
−= 6)
22
(1)23.
xyxyx
′′′
++=
2.2. Решите задачу Коши:
1)
,
x
eyx
′′′
=−
(0)3,
y
=
(0)1,
y
′
=−
(0)0;
y
′′
=
2)
2
()0,
yy
′′′′′
+=
(1)1,
y
=−
(1)0,
y
′
=
(1)1;
y
′′
=
3)
3
1,
yy
′′
=
1
1,
2
y
=
1
1;
2
y
′
=
4)
2
(31)30,
yyy
′′′
+−=
(1)0,
y
=
(1)1.
y
′
=
III уровень
3.1. Решите задачу Коши:
1)
30,
yyy
′′′′
−=
(0)2,
y
=−
(0)0,
y
′
=
9
(0);
2
y
′′
=
2)
2
2
10,
yy
yy
′′′
−+=
(0)1,
y
=
(0)1;
y
′
=
3)
43
0,
yyy
′′
−=
(0)1,
y
=
(0)2;
y
′
=
4)
( )
2
2
1,
x
yxye
′′′
+=
(0)1,
y
=
(0)0;
y
′
=
5)
22
()ln,
yyyyy
′′′
−=
(0)1,
y
=
(0)1.
y
′
=
3.2. Найдите дифференциальное уравнение семейства ок-
ружностей
22
12
()()4.
xCyC
−+−=
3.3. Составьте дифференциальное уравнение семейства пло-
ских кривых
22
123
0.
xyCxCyC
++++=
3.4. Покажите, что функция
(),
yyx
=
параметрически за-
данная системой уравнений
2
3
13
ln,
2
4
13
,0,
4
4
xt
t
ytt
t
=+
=+>
является решением уравнения
2
()230.
yyy
′′′′′
−+=
205
22.6. Линейные однородные дифференциальные
уравнения высших порядков
Линейным однородным дифференциальным уравнением
n-го порядка называется уравнение
(
)
1
()
110
()...()()0.
n
n
n
yaxyaxyaxy
−
−
′
++++=
(22.55)
Общим решением этого уравнения является функция
1122
...,
nn
yCyCyCy
=+++
где
12
,,...,
n
yyy
– линейно-независимые частные решения
уравнения (22.55),
12
,,...,
n
CCC
– произвольные постоянные.
Совокупность n линейно-независимых на (a, b) решений
уравнения (22.55) называется фундаментальной системой ре-
шений.
Частным случаем уравнения (22.55) является линейное од-
нородное уравнение n-го порядка с постоянными коэффициен-
тами:
(
)
(
)
(
)
12
1210
...0,
nnn
nn
yayayayay
−−
−−
′
+++++=
(22.56)
где
0121
,,,...,
n
aaaa
−
– действительные числа.
Для нахождения частных решений уравнения (22.56) со-
ставляют характеристическое уравнение
1
110
...0
nn
n
aaaλλλ
−
−
++++=
(22.57)
путем замены в уравнении (22.56) производных определенного
порядка на соответствующие степени параметра
:
λ
(
)
k
y
на
,
k
λ
где
0,1,...,.
kn
=
Каждому корню уравнения (22.57) соответствует опреде-
ленное частное решение дифференциального уравнения. Вид ча-
стного решения зависит от типа корня уравнения (22.57). Воз-
можны следующие четыре случая, которые определяет правило
частных решений:
1. Если
0
λ
– действительный корень кратности 1 (простой
корень), то ему соответствует решение вида
0
.
x
ye
λ
=
2. Если
1
λ
– действительный корень кратности k, то ему со-
ответствует k частных решений:
111
1
12
,,...,.
xxx
k
k
yeyxeyxe
λλλ
−
===
206
3. Если
2,3
i
λαβ
=±
– пара комплексно-сопряженных кор-
ней, то им соответствует два частных решения:
1
cos,
x
yex
α
β
=
2
sin.
x
yex
α
β
=
4. Если
4,5
i
λαβ
=±
– пара k-кратных комплексно-сопря-
женных корней, то им соответствуют 2k частных решения:
1
12
cos,cos,...,cos,
xxkx
k
yexyxexyxex
ααα
βββ
−
===
1
122
sin,sin,...,sin.
xxkx
kkk
yexyxexyxex
ααα
βββ
−
++
===
Поскольку характеристическое уравнение (22.57) имеет n
корней, считая их кратность, то для дифференциального уравне-
ния (22.56) по правилу частных решений можно указать n реше-
ний
12
,,...,.
n
yyy
Эти решения образуют фундаментальную сис-
тему решений.
Тогда общее решение уравнения (22.56) определяется фор-
мулой
1122
()()...(),
nn
yCyxCyxCyx
=+++
где
12
,,...,
n
CCC
– произвольные постоянные.
Пример 1. Найти общее решение уравнения:
1)
250;
yy
′′
−=
2)
250;
yy
′′′
−=
3)
440;
yyy
′′′
−+=
4)
220.
yyy
′′′
−+=
Решение. 1) Составим характеристическое уравнение
2
250.
λ
−=
Решая его, получаем:
1
5,
λ
=
2
5
λ
=−
– два действительных про-
стых корня. Им соответствуют частные решения
5
1
,
x
ye
=
5
2
.
x
ye
−
=
Общее решение заданного дифференциального уравнения имеет вид:
55
12
,
xx
yCeCe
−
=+
где
12
,
CC
– произвольные постоянные.
2) Составим характеристическое уравнение
2
250.
λλ
−=
Решая его, получаем:
1
0,
λ
=
2
25
λ
=
– два действительных про-
стых корня. Им соответствуют частные решения
1
1,
y
=
25
2
.
x
ye=
Общее решение заданного дифференциального уравнения имеет вид:
25
12
,
x
yCCe=+
где
12
,
CC
– произвольные постоянные.
207
3) Характеристическое уравнение имеет вид:
2
440
λλ
−+=
или
2
(2)0.
λ
−=
Отсюда
2
λ
=
– корень кратности 2.
Тогда решения
2
1
x
ye
= и
2
2
x
yxe
= образуют фундаментальную
систему решений исходного дифференциального уравнения, а общее
решение имеет вид:
22
12
,
xx
yCeCxe
=+
где
12
,
CC
– произвольные постоянные.
4) Характеристическое уравнение заданного дифференциального
уравнения
2
220.
λλ
−+=
Его корни:
1
1,
i
λ
=+
2
1
i
λ
=−
– простые комплексно-сопряжен-
ные. Тогда этой паре корней характеристического уравнения соответ-
ствуют два линейно-независимых частных решения заданного диффе-
ренциального уравнения:
1
cos,
x
yex
=
2
sin.
x
yex
=
Получаем общее решение исходного дифференциального уравнения:
12
cossin,
xx
yCexCex
=+
где
12
,
C
С
– произвольные постоянные.
Пример 2. Найти общее решение дифференциального уравнения:
1)
320;
yyy
′′′′′′
−+=
2)
3420;
yyyy
′′′′′′
+++=
3)
450;
IV
yyy
′′′′′
−+=
4)
330.
VIIV
yyyy
′′
+++=
Решение. 1) Запишем характеристическое уравнение заданного
дифференциального уравнения
32
320.
λλλ
−+=
Его корнями будут
1
0,
λ
=
2
1,
λ
=
3
2,
λ
=
т. е. корни характери-
стического уравнения действительные и различные. Им соответствуют
три линейно-независимых частных решения:
1
1,
y
=
2
,
x
ye
=
2
3
.
x
ye
=
Общее решение заданного дифференциального уравнения имеет
вид:
2
123
,
xx
yCCeCe
=++
где
123
,,
C
С C
– произвольные постоянные.
2) Составим характеристи ческое уравнение заданного дифферен-
циального уравнения
32
3420.
λλλ
+++=
Его корни:
1
1,
λ
=−
2
1,
i
λ
=−+
3
1.
i
λ
=−−
Им соответствуют три
208
линейно-независимых частных решения:
1
,
x
ye
−
=
2
cos,
x
yex
−
=
3
sin.
x
yex
−
=
Общее решение имеет вид:
123
cossin,
xxx
yCeCexCex
−−−
=++
где
123
,,
CCC
– произвольные постоянные.
3) Характеристическое уравнение имеет вид:
432
450.
λλλ
−+=
Его корни:
1,2
0
λ
=
(корень кратности 2),
3
2,
i
λ
=+
4
2.
i
λ
=−
Им
соответствуют четыре линейно-независимых частных решения вида
1
1,
y
=
2
,
yx
=
2
3
cos,
x
yex
=
2
4
sin.
x
yex
=
Общее решение имеет вид:
22
1234
cossin,
xx
yCCxCexCex
=+++
где
1234
,,,
CCCC
– произвольные постоянные.
4) Запишем характеристическое уравнение заданного дифферен-
циального уравнения
642
3310.
λλλ
+++=
Преобразуем это уравнение к виду
23
(1)0.
λ
+=
Отсюда, очевидно, что корни характеристического уравнения
1
,
i
λ
=
2
i
λ
=−
– комплексно-сопряженные кратности 3. Тогда им со-
ответствуют шесть линейно-независимых частных решений вида
1
cos,
yx
=
2
sin,
yx
=
3
cos,
yxx
=
4
sin,
yxx
=
2
5
cos,
yxx
=
2
6
sin.
yxx
=
Общее решение заданного дифференциального уравнения имеет вид:
22
123456
cossincossincossin,
yCxCxCxxCxxCxxCxx
=+++++
где
123456
,,,,,
CCCCCC
– произвольные постоянные.
Пример 3. Решить задачу Коши:
1)
(
)
690,(0)2,09;
yyyyy
′′′′
−+===
2)
(
)
(
)
40,(0)2,(0)3,(0)4,08,016.
VIV
yyyyyyy
′′′′′′′′′
+======
Решение. 1) Характеристическое уравнение имеет вид:
2
690
λλ
−+=
или
2
(3)0.
λ
−=
Его корень
3
λ
=
– корень кратности 2. Тогда решения
3
1
,
x
ye
=
3
2
x
yxe
= образуют фундаментальную систему решений. Общее реше-
ние имеет вид:
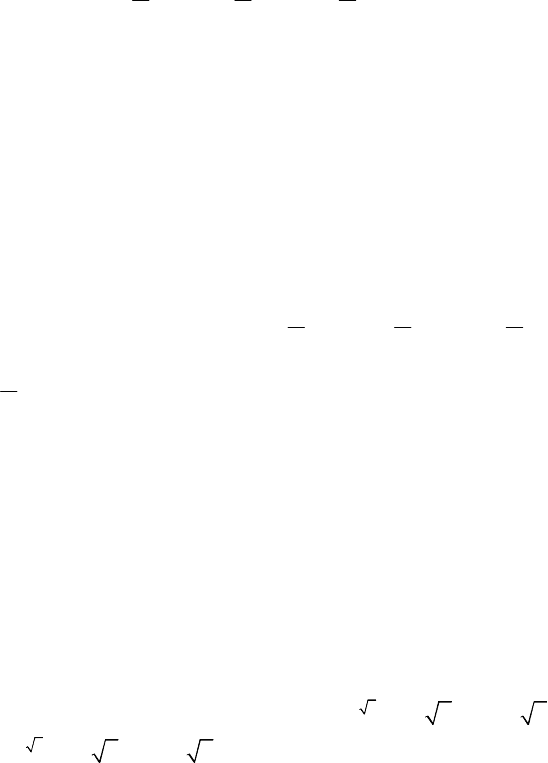
209
33
12
.
xx
yCeCxe
=+
Чтобы найти константы
1
C
и
2
,
C
дифференцируем найденное
общее решение:
333
122
33.
xxx
yCeCeCxe
′
=++
Затем подставляем начальные условия в выражения для y и
y
′
и
решаем систему уравнений относительно
1
C
и
2
:
C
0
1
00
12
2,
93.
Ce
CeCe
=
=+
Получаем
1
2,
C
=
2
3.
C
=
Тогда решение задачи Коши:
33
23.
xx
yexe
=+
2) Характеристическое уравнение
53
40
λλ
+=
или
32
(4)0.
λλ
+=
Его корни:
1,2,3
0
λ
=
– корень кратности 3,
4
2,
i
λ
=
5
2.
i
λ
=−
Им
соответствуют пять линейно-независимых решений:
2
12345
1,,,cos2,sin2.
yyxyxyxyx
=====
Общее решение заданного дифференциального уравнения имеет вид:
2
12345
cos2sin2.
yCCxCxCxCx
=++++
Для определения констант
12345
,,,,
CCCCC
продифференцируем
полученное общее решение последовательно четыре раза:
2345
22sin22cos2;
yCCxCxCx
′
=+−+
345
24cos24sin2;
yCCxCx
′′
=−−
45
8sin28cos2;
yCxCx
′′′
=−
45
16cos216sin2.
IV
yCxCx
=+
Подставляя в выражения для
,,,,
IV
yyyyy
′′′′′′
начальные усло-
вия, находим константы:
5
1,
C
=−
4
1,
C
=
3
4,
C
=
2
5,
C
=
1
1.
C
=
Тогда решение задачи Коши:
2
154cos2sin2.
yxxxx
=+++−
Задания
I уровень
1.1. Решите уравнение:
1)
2520;
yyy
′′′
−+=
2)
160;
yy
′′
+=
210
3)
40;
yy
′′
−=
4)
220.
IV
yyy
′′′′′
++=
1.2. Решите задачу Коши:
1)
20,(0)1,(0)2;
yyyyy
′′′′
++===
2)
560,(0)2,(0)3,(0)4;
yyyyyy
′′′′′′′′′
−+====
3)
90,1,1,1;
222
yyyyy
πππ
′′′′′′′
+====
4)
160,(1)1,(1)2,(1)3,(1)4.
IV
yyyyyy
′′′′′′
−=====
II уровень
2.1. Решите уравнение:
1)
290;
yyy
′′′′′′
++=
2)
80;
yy
′′′
+=
3)
80;
IV
yy
′
−=
4)
440.
IV
yyyy
′′′′′′
−+−=
2.2. Решите задачу Коши:
1)
20,(0)1,(0)1,(0)1;
yyyyy
′′′′′′
+====
2)
48840,
IV
yyyyy
′′′′′′
−+−+=
1,
2
y
π
=
2,
2
y
π
′
=
3,
2
y
π
′′
=
4.
2
y
π
′′′
=
3)
8160,
VIV
yyy
′′′
−+=
(0)4,
y
=
(0)3,
y
′
=
(0)2,
y
′′
=
(
)
01,
y
′′′
=
(0)1.
IV
y
=
III уровень
3.1. Составьте линейное дифференциальное уравнение по
его фундаментальной системе решений:
1)
,;
xx
exe
−−
2)
2
1,,,cos,sin;
xxxx
3)
2
1,,;
xx
4)
cos,sin.
xx
exex
−−
3.2. Докажите, что функции
2
1
(cos2sin2),
x
yexix
=+
2
2
(cos2sin2)
x
yexix
−
=− образуют фундаментальную сис-
тему решений уравнения
40.
yiy
′′
−=
Проверьте:

211
1) являются ли решениями данного уравнения функции
11
Re,
uy
=
22
Re,
uy
=
11
Im,
vy
=
22
Im;
vy
=
2) имеет ли данное уравнение действительные решения.
22.7. Линейные неоднородные дифференциальные
уравнения
Линейным неоднородным дифференциальным уравнением
n-го порядка называется уравнение вида
()(1)
110
()...()()(),
nn
n
yaxyaxyaxyfx
−
−
′
++++= (22.58)
где
012
(),(),(),...,()
axaxaxfx
– непрерывные функции на
некотором промежутке (a, b).
Если
()0
fx
≡
в уравнении (22.58), то получаем соответ-
ствующее однородное дифференциальное уравнение
()1
110
()...()()0.
nn
n
yaxyaxyaxy
−
−
′
++++=
(22.59)
Общее решение уравнения (22.58) определяется формулой
0
,
ч
yyy
=+
(22.60)
где
0
y
– общее решение соответствующего однородного
уравнения,
ч
y
– частное решение неоднородного уравнения.
Для решения дифференциального уравнения (22.58) исполь-
зуют метод Лагранжа (метод вариации произвольных постоян-
ных). Для его реализации необходимо сделать следующее:
1. Записать соответствующее однородное дифференциаль-
ное уравнение.
2. Найти фундаментальную систему частных решений
1122
(),(),...,()
nn
yyxyyxyyx
===
соответствующего однородного дифференциального уравнения.
3. Найти общее решение однородного уравнения в виде
1122
...,
nn
yCyCyCy
=+++
(22.61)
где
12
,,...,
n
CCC
– константы.
4. Решение заданного неоднородного дифференциального
уравнения искать в виде (22.61), но считать, что
11
(),
CCx
=
22
(),...,()
nn
CCxCCx
==
– функциональные коэффициенты,
которые надо найти.
212
5. Для нахождения коэффициентов
(1,)
k
Ckn
= решения
уравнения (22.61) необходимо записать систему уравнений
1122
1122
(2)(2)
1122
()()()()...()()0,
()()()()...()()0,
...........................................................................,
()()()()...
nn
nn
nn
CxyxCxyxCxyx
CxyxCxyxCxyx
CxyxCxyx
−−
′′′
+++=
′′′′′′
+++=
′′
++
(2)
(1)(1)(1)
1122
()()0,
()()()()...()()().
n
nn
nnn
nn
Cxyx
CxyxCxyxCxyxfx
−
−−−
′
+=
′′′
+++=
(22.62)
6. Решить систему (22.62) относительно
1
,...,
n
CC
′′
и получить
11
()(),,()().
nn
CxxCxx
ϕϕ
′′
==
K
7. Проинтегрировать полученные равенства для
(),
k
Cx
′
1,
kn
=
и найти
111
()(),...,()(),
nnn
CxxdxCCxxdxC
ϕϕ
=+=+
∫∫
где
1
,...,
n
CC
– произвольные постоянные.
8. Подставить полученные выражения вместо
12
,,...,
n
CCC
в
записанное решение (22.61). Это и есть общее решение заданно-
го дифференциального уравнения (22.58).
Согласно методу Лагранжа, сразу находим общее решение
(22.60) заданного дифференциального уравнения (22.58) (без на-
хождения отдельно его частного решения
ч
y
).
Для решения линейных неоднородных дифференциальных
уравнений (22.58) с постоянными коэффициентами и правой ча-
стью f(x) специального вида используют метод Эйлера (метод
неопределенных коэффициентов). Этот метод применим, если
функция f(x) имеет вид:
(
)
()()cos()sin,
x
nm
fxePxxQxx
α
ββ=+ (22.63)
где
,,
αβ
∈
R
(),
n
Px
()
m
Qx
– многочлены степени n и m со-
ответственно.
Для реализации метода необходимо сделать следующее:
1. Решить соответствующее однородное дифференциальное
уравнение (22.59), используя характеристическое уравнение:
1
110
...0.
nn
n
aaaλλλ
−
−
++++=
(22.64)
Общее решение дифференциального уравнения (22.59) за-
писать в виде
01122
...,
nn
yCyCyCy
=+++
(22.65)
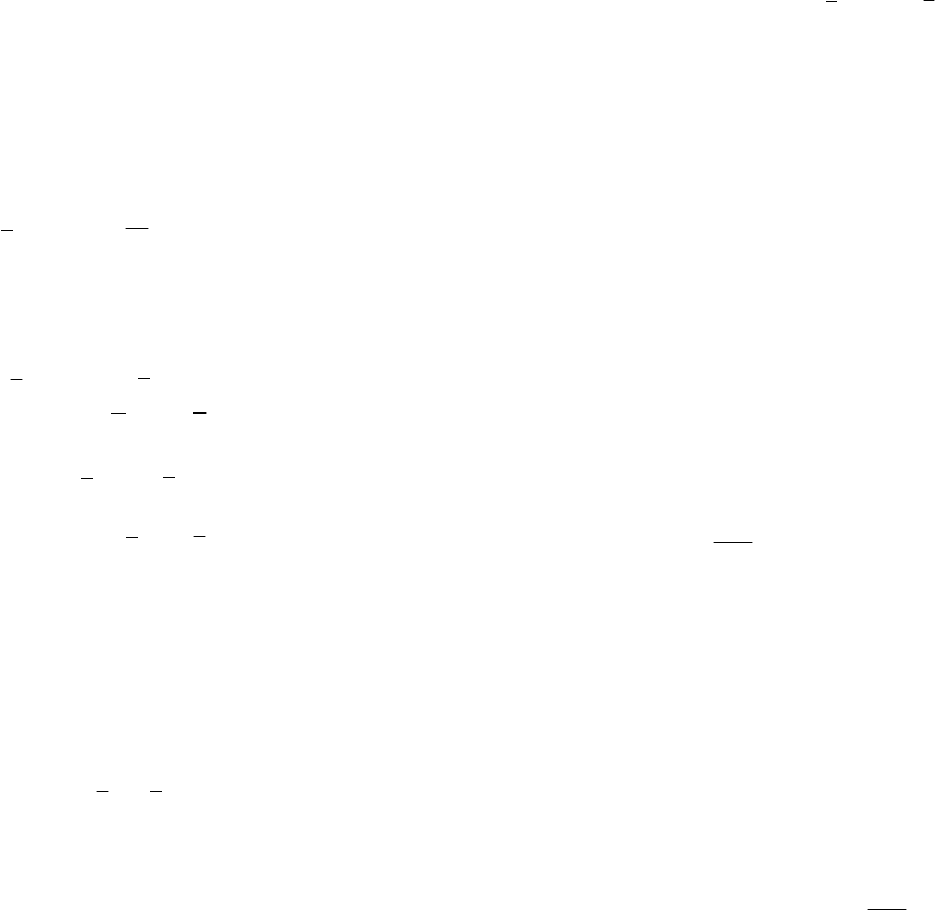
213
где
12
,,...,
n
yyy
– частные решения уравнения (22.59), полу-
ченные в соответствии с типом корней характеристического
уравнения (22.64).
2. Записать контрольное число
,
i
σαβ
=+
где
,
αβ
– числа,
которые заданы в (22.63). Определить, имеется ли число
σ
сре-
ди корней уравнения (22.64). Если имеется, то какова кратность
k этого корня.
3. Если
i
σαβ
=+
не содержится среди корней характери-
стического уравнения (22.64), то записать искомое частное ре-
шение
ч
y
дифференциального уравнения (22.58) в виде
(()cos()sin).
x
ч rr
yePxxQxx
α
ββ
=+ (22.66)
Если среди корней характеристического уравнения (22.64)
имеется корень
,
i
σαβ
=+
кратность которого k, то искомое ча-
стное решение
ч
y
дифференциального уравнения (22.58) запи-
сать в виде
(()cos()sin),
kx
ч rr
yxePxxQxx
α
ββ
=+ (22.67)
где в равенствах (22.66) и (22.67)
(),
r
Px
()
r
Qx
– многочлены
степени r,
max(,)
rnm
=
– бóльшая степень заданных много-
членов в (22.63). Многочлены
()
r
Px
и
()
r
Qx
необходимо запи-
сать в стандартном виде с буквенными коэффициентами.
4. Коэффициенты многочленов
(),
r
Px
()
r
Qx
найти методом
неопределенных коэффициентов. Для этого необходимо вычис-
лить производные
(
)
,,,
n
ччч
yyy
′′′
K функции (22.66) или (22.67) и
подставить в левую часть уравнения (22.58). Далее надо привес-
ти подобные относительно
cos
x
β
и
sin,
x
β
а затем приравнять
многочлены при одноименных тригонометрических функциях.
Используя равенство многочленов, записывают систему уравне-
ний относительно искомых числовых коэффициентов.
5. Найденные значения числовых коэффициентов необхо-
димо подставить в многочлены
r
P
и
r
Q
частного решения
ч
y
,
записанного в виде функции (22.66) или (22.67).
6. Записать общее решение заданного дифференциального
уравнения (22.58) в виде (22.60), где решение
0
y
имеет вид (22.65),
а
ч
y
– решение вида, записанного в предыдущем 5-м «шаге».
214
З а м е ч а н и е 1. Форма записи (22.66) или (22.67) сохраняется и в
случаях, когда в исходном уравнении (22.58) ()
n
Pxa
=
или
(),
m
Qxb
=
где a, b – числа. Тогда
(),
r
PxA
=
(),
r
QxB
=
где A, B – числа, которые
надо найти.
З а м е ч а н и е 2. Если правая часть уравнения (22.58) есть сумма
различных функций специального вида, то для нахождения y
ч
использу-
ют теорему о наложении решений: если в уравнении (22.58) правая
часть имеет вид:
12
()()()...(),
k
fxfxfxfx
=+++
где
,
k ∈
N
а
12
,,...,
k
÷÷÷
yyy
– частные решения уравнений
()(1)
101
()(1)
102
()(1)
10
()...()(),
()...()(),
........................................
.......................
()...()(),
nn
n
nn
n
nn
nk
yaxyaxyfx
yaxyaxyfx
yaxyaxyfx
−
−
−
−
−
−
+++=
+++=
+++=
соответственно, то функция
12
...
k
чччч
yyyy
=+++
является решением заданного уравнения.
3. Если в правой части f(x) уравнения (22.58) присутствует только
одно слагаемое с тригонометрической функцией (т. е.
cos
n
Px
β
или
sin
m
Qx
β
), то общее решение и в этом случае записывают в виде
(22.66) или (22.67), т. е. с двумя тригонометрическими функциями.
Пример 1. Решить уравнение методом Лагранжа:
1)
1
;
sin
yy
x
′′
+= 2)
44;
yyx
′′
−= 3)
46.
x
yyyye
′′′′′′
++−=
Решение. 1) Это неоднородное линейное дифференциальное урав-
нение 2-го порядка. Найдем решение соответствующего однородного
уравнения
0.
yy
′′
+=
Его характеристическое уравнение
2
10,
λ
+=
корни которого
1
,
i
λ
=−
2
i
λ
=
– комплексно-сопряженные, простые. Тогда общее ре-
шение соответствующего однородного уравнения
012
cossin,
yCxCx
=+
где C
1
, C
2
– произвольные постоянные.
Общее решение заданного дифференциального уравнения ищем в виде
12
cossin,
yCxCx
=+ (22.68)
где
11
(),
CCx
=
22
()
CCx
= – функции, которые надо найти.
Для нахождения C
1
(x), C
2
(x) решим систему уравнений
12
12
cossin0,
1
(cos)(sin).
sin
CxCx
CxCx
x
′′
+=
′′′′
+=
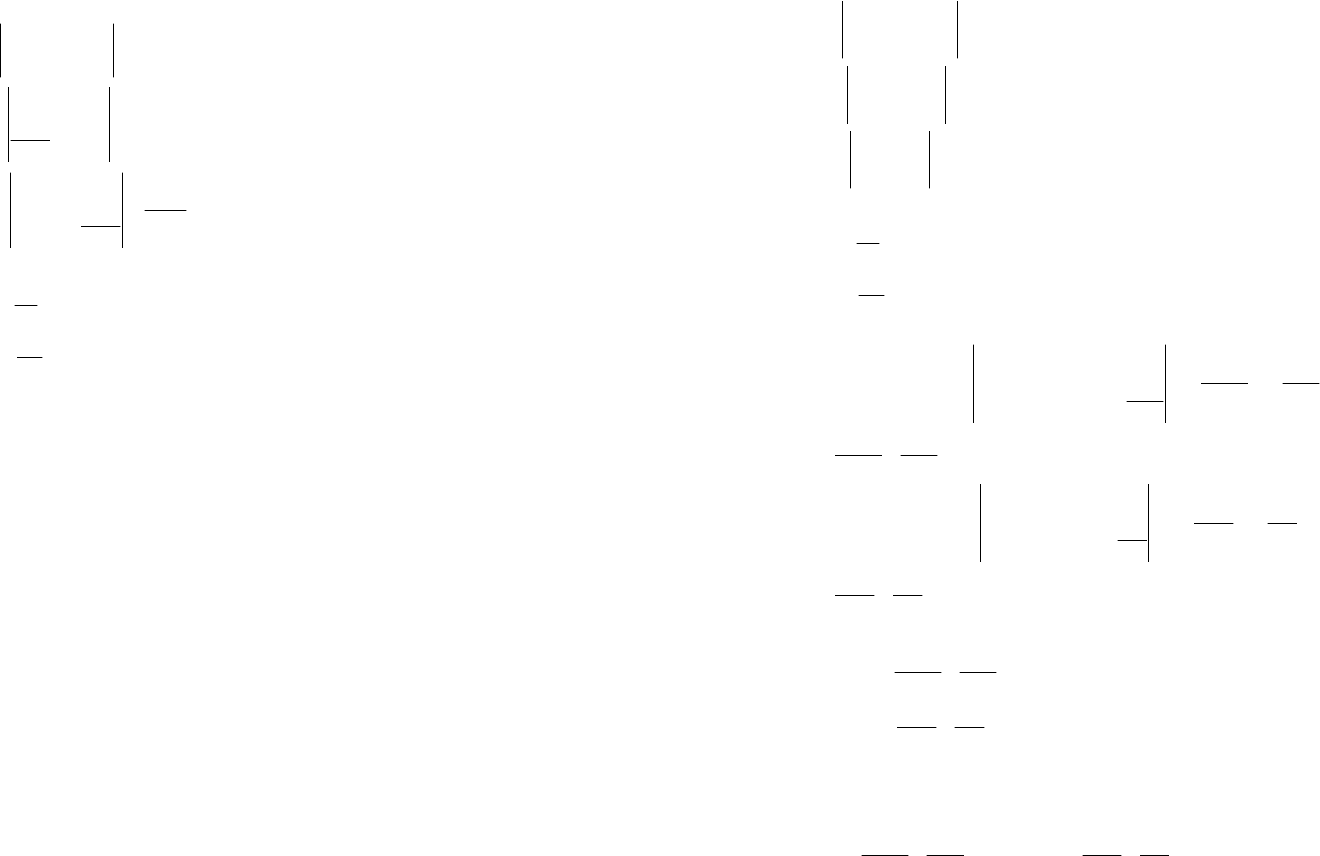
215
Используем, например, метод Крамера:
22
cossin
cossin1,
sincos
xx
xx
xx
∆==+=
−
1
0sin
1,
1
cos
sin
x
x
x
∆==−
2
cos0
cos
ctg.
1
sin
sin
sin
x
x
x
x
x
x
∆===
−
Тогда решениями системы будут:
1
1
2
2
,
C
C
∆
′
=
∆
∆
′
=
∆
или
1
2
1,
ctg.
C
Cx
′
=−
′
=
Интегрируя полученные равенства, получаем:
11
22
(),
()ln|sin|,
CxxC
CxxC
=−+
=+
где
12
,
CC
– произвольные постоянные.
Подставляем найденные значения функций в (22.68) и получаем
общее решение заданного дифференциального уравнения:
12
cossincossinln|sin|.
yCxCxxxxx
=+−+
2) Это неоднородное линейное дифференциальное уравнение 2-го
порядка. Найдем решение соответствующего однородного уравнения:
40.
yy
′′
−=
Его характеристическое уравнение
2
40,
λ
−=
корни кото-
рого
1
2,
λ
=
2
2
λ
=−
– простые, действительные. Тогда общее решение
соответствующего однородного уравнения
22
012
,
xx
yCeCe
−
=+ где
12
,
CC
– произвольные постоянные.
Общее решение заданного дифференциального уравнения ищем
в виде
22
12
,
xx
yCeCe
−
=+ (22.69)
где
11
(),
CCx
=
22
()
CCx
= – функции, которые надо найти.
Для нахождения
1
(),
Cx
2
()
Cx
решим систему уравнений
22
12
22
12
0,
()()4.
xx
xx
CeCe
CeCex
−
−
′′
+=
′′′′
+=
Используем метод Крамера:
216
22
00
22
224,
22
xx
xx
ee
ee
ee
−
−
∆==−−=−
−
2
2
1
2
0
4,
42
x
x
x
e
xe
xe
−
−
−
∆==−
−
2
2
2
2
0
4.
24
x
x
x
e
xe
ex
∆==
Тогда решение системы:
1
1
2
2
,
C
C
∆
′
=
∆
∆
′
=
∆
или
2
1
2
2
,
.
x
x
Cxe
Cxe
−
′
=
′
=−
Интегрируем полученные равенства:
()
22
2
2
1
2
,
22
,
2
xx
x
x
x
uxdudx
xee
Cxxedxdx
e
dvedxv
−−
−
−
−
==
===−+=
==−
∫∫
22
1
,
24
xx
xee
C
−−
=−−+
()
22
2
2
2
2
,,
22
,
2
xx
x
x
x
uxdudx
xee
Cxxedxdx
e
dvedxv
==
=−==−−=
==
∫∫
22
2
.
24
xx
xee
C
=−++
Таким образом,
22
11
22
22
(),
24
(),
24
xx
xx
xee
CxC
xee
CxC
−−
=−−+
=−++
где
12
,
CC
– произвольные постоянные. Подставляем найденные
значения функций в (22.69) и получаем общее решение заданного
дифференциального уравнения:
2222
22
12
.
2424
xxxx
xx
xeexee
yCeCe
−−
−
=−−++−++
После упрощения приходим к ответу:
22
12
.
xx
yCeCex
−
=+−
3) Это неоднородное линейное дифференциальное уравнение 3-го
порядка. Найдем решение соответствующего однородного уравнения
