Майсеня Л.И. Математика в примерах и задачах. Часть 4
Подождите немного. Документ загружается.


217
460.
yyyy
′′′′′′
++−=
Его характеристическое уравнение
32
460,
λλλ
++−=
корни ко-
торого
1
1,
λ
=
2
2,
λ
=−
3
3
λ
=−
– действительные, простые. Тогда об-
щее решение соответствующего однородного уравнения
23
0123
,
xxx
yCeCeCe
−−
=++ где
123
,,
CCC
– произвольные постоянные.
Общее решение заданного дифференциального уравнения ищем в виде
23
123
,
xxx
yCeCeCe
−−
=++ (22.70)
где
112233
(),(),()
CCxCCxCCx
=== – функции, которые надо
найти. Для нахождения
123
(),(),()
CxCxCx
решаем систему уравнений
23
123
23
123
23
123
0,
230,
49.
xxx
xxx
xxxx
CeCeCe
CeCeCe
CeCeCee
−−
−−
−−
′′′
++=
′′′
−−=
′′′
++=
По методу Крамера:
2323
23
2323
23
2323
34
23034
38
49038
xxxxxx
xx
xxxxxx
xx
xxxxx
eeeeee
ee
eeeeee
ee
eeeee
−−−−
−−
−−−−
−−
−−−−
−−
∆=−−=−−==
5554
(2412)(12)12,
xxxxxx
eeeeee
−−−−
=−+=−=−
23
23
23554
1
23
23
0
023(32),
23
49
xx
xx
xxxxxxx
xx
xxx
ee
ee
eeeeeee
ee
eee
−−
−−
−−−−−
−−
−−
∆=−−==−+=−
−−
3
3
322
2
3
3
0
03(3)4,
3
9
xx
xx
xxxxxxx
xx
xxx
ee
ee
eeeeeee
ee
eee
−
−
−−−−
−
−
∆=−=−=−−−=
−
2
2
2
3
2
2
0
20(2)3.
2
4
xx
xx
xxxxxx
xx
xxx
ee
ee
eeeeee
ee
eee
−
−
−−−
−
−
∆=−==−−=−
−
Тогда решение системы:
1
1
2
2
3
3
,
,
C
C
C
∆
′
=
∆
∆
′
=
∆
∆
′
=
∆
или
1
3
2
4
3
1
,
12
,
3
.
4
x
x
C
e
C
e
C
′
=
′
=−
′
=
218
Интегрируя полученные равенства, получаем:
11
3
22
4
33
(),
12
(),
9
(),
16
x
x
x
CxC
e
CxC
e
CxC
=+
=−+
=+
где
123
,,
CCC
– произвольные постоянные.
Подставляем найденные значения функций в (22.70) и получаем
общее решение заданного дифференциального уравнения:
34
23
123
.
12916
xx
xxx
xee
yCeCeCe
−−
=++−+++
После упрощения приходим к ответу:
23
123
7
.
12144
xxxx
x
yCeCeCee
−−
=+++−
Пример 2. Решить задачу Коши:
1)
8
9ctg3,0,;
663
yyxyy
ππ
′′′
+===−
2)
2
15
4,(0)2,(0),(0)4.
8
yyxyyy
′′′′′′′
+====
Решение. 1) Это линейное неоднородное дифференциальное урав-
нение 2-го порядка. Найдем общее решение соответствующего одно-
родного уравнения
90.
yy
′′
+=
Его характеристическое уравнение
2
90,
λ
+=
корни которого
1
3,
i
λ =
2
3
i
λ
=−
– комплексно-сопряжен-
ные, простые. Тогда общее решение соответствующего однородного
уравнения
01212
cos3sin3,,.
yCxCxCCconst
=+= Общее решение за-
данного дифференциального уравнения ищем в виде
12
cos3sin3,
yCxCx
=+
где
1122
(),()
CCxCCx
== – функции, для нахождения которых
составляем систему
12
12
cos3sin30,
3sin33cos3ctg3.
CxCx
CxCxx
′′
+=
′′
−+=
Решаем ее методом Крамера:
cos3sin3
3,
3sin33cos3
xx
xx
∆==
−
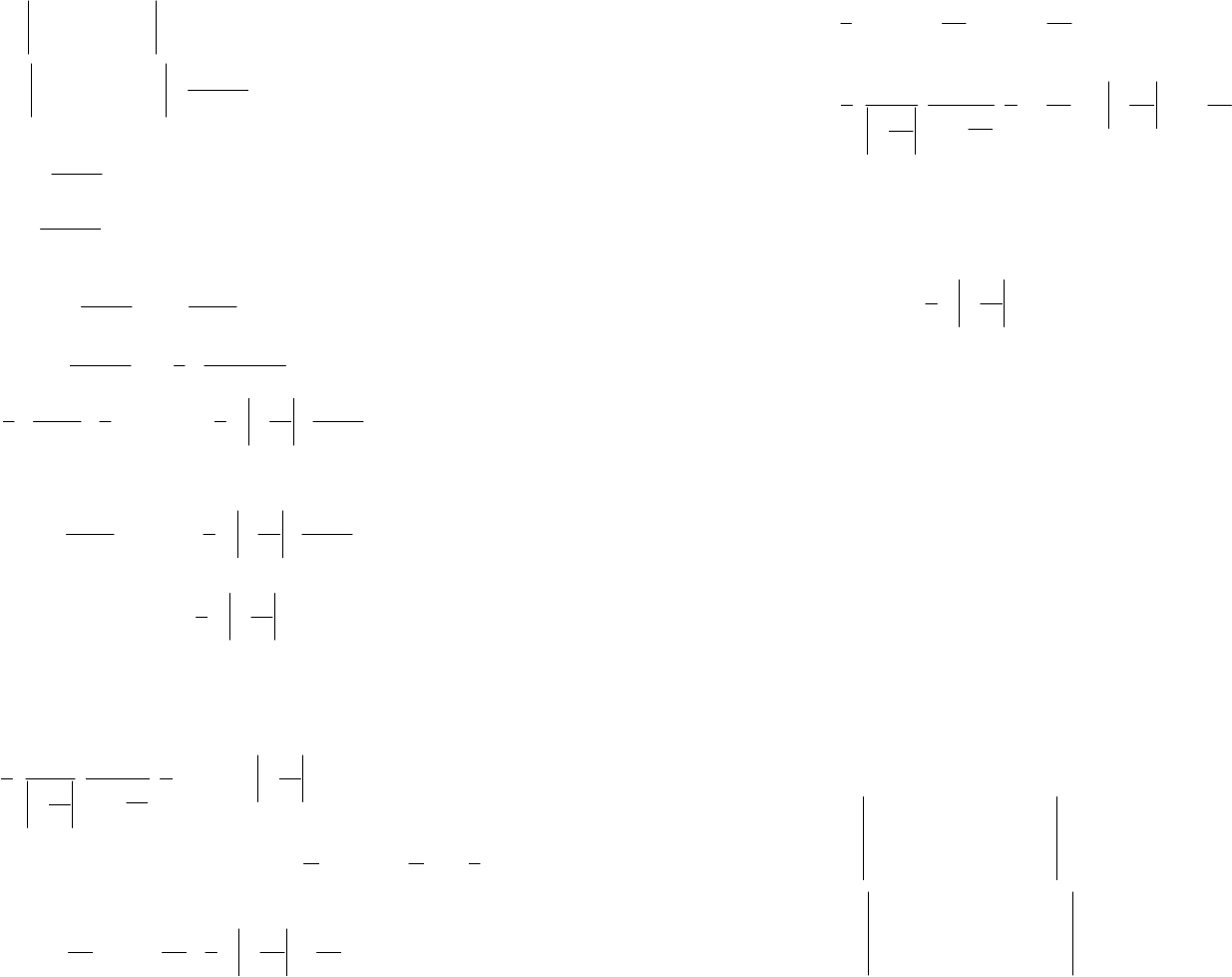
219
1
0sin3
cos3,
ctg33cos3
x
x
xx
∆==−
2
2
cos30
cos3
.
sin3
3sin3ctg3
x
x
x
xx
∆==
−
Получаем решение системы:
1
2
2
cos3
,
3
cos3
.
3sin3
x
C
x
C
x
′
=−
′
=
Интегрируем полученные равенства:
11
cos3sin3
(),
39
xx
CxdxC
=−=−+
∫
22
2
cos311sin3
()
3sin33sin3
xx
Cxdxdx
xx
−
===
∫∫
2
1113cos3
sin3lntg,
3sin33929
dxxx
xdxC
x
=−=++
∫∫
где
12
,
CC
– произвольные постоянные.
Тогда общее решение заданного дифференциального уравнения:
12
sin313cos3
cos3lntgsin3.
9929
xxx
yCxCx
=−+++
После упрощения получаем:
12
13
cos3sin3lntgsin3.
92
x
yCxCxx
=++
Далее решаем задачу Коши. Дифференцируем полученное общее
решение:
12
3sin33cos3
yCxCx
′
=−++
2
11133
sin3lntg3cos3.
3
9223
cos
tg
2
2
x
xx
x
x
+⋅⋅+⋅
Подставляем начальные условия
0,
6
y
π
=
8
63
y
π
′
=−
в выра-
жения для y и
y
′
и определяем константы
1
C
и
2
:
C
12
33133
0cossinlntgsin,
669126
CC
ππππ
=++
220
12
833
3sin3cos
366
CC
ππ
−=−++
2
1113333
sinlntg3cos.
3
926126
3
cos
tg
12
12
πππ
π
π
+⋅⋅+⋅
Отсюда имеем:
1
2
1,
0.
C
C
=
=
Получаем решение задачи Коши:
13
cos3lntgsin3.
92
x
yxx
=+
2) Это линейное неоднородное дифференциальное уравнение 3-го
порядка. Найдем его общее решение методом Лагранжа. Соответст-
вующее однородное уравнение имеет вид:
40.
yy
′′′′
+=
Его характери-
стическое уравнение
3
40,
λλ
+=
где
1
0,
λ
=
2
2,
i
λ
=
3
2
i
λ
=−
– корни.
Тогда общее решение однородного дифференциального уравнения:
0123
cos2sin2.
yCCxCx
=++
Общее решение заданного дифференциального уравнения ищем
в виде
123
cos2sin2,
yCCxCx
=++
где
11
(),
CCx
=
22
(),
CCx
=
33
()
CCx
= – искомые функциональ-
ные коэффициенты.
Составляем систему
123
23
2
23
cos2sin20,
2sin22cos20,
4cos24sin2.
CCxCx
CxCx
CxCxx
′′′
++=
′′
−+=
′′
−−=
Решаем ее методом Крамера:
22
1cos2sin2
02sin22cos28sin28cos28,
04cos24sin2
xx
xxxx
xx
∆=−=+=
−−
2222
1
2
0cos2sin2
02sin22cos2(2cos22sin2)2,
4cos24sin2
xx
xxxxxx
xxx
∆=−=+=
−−
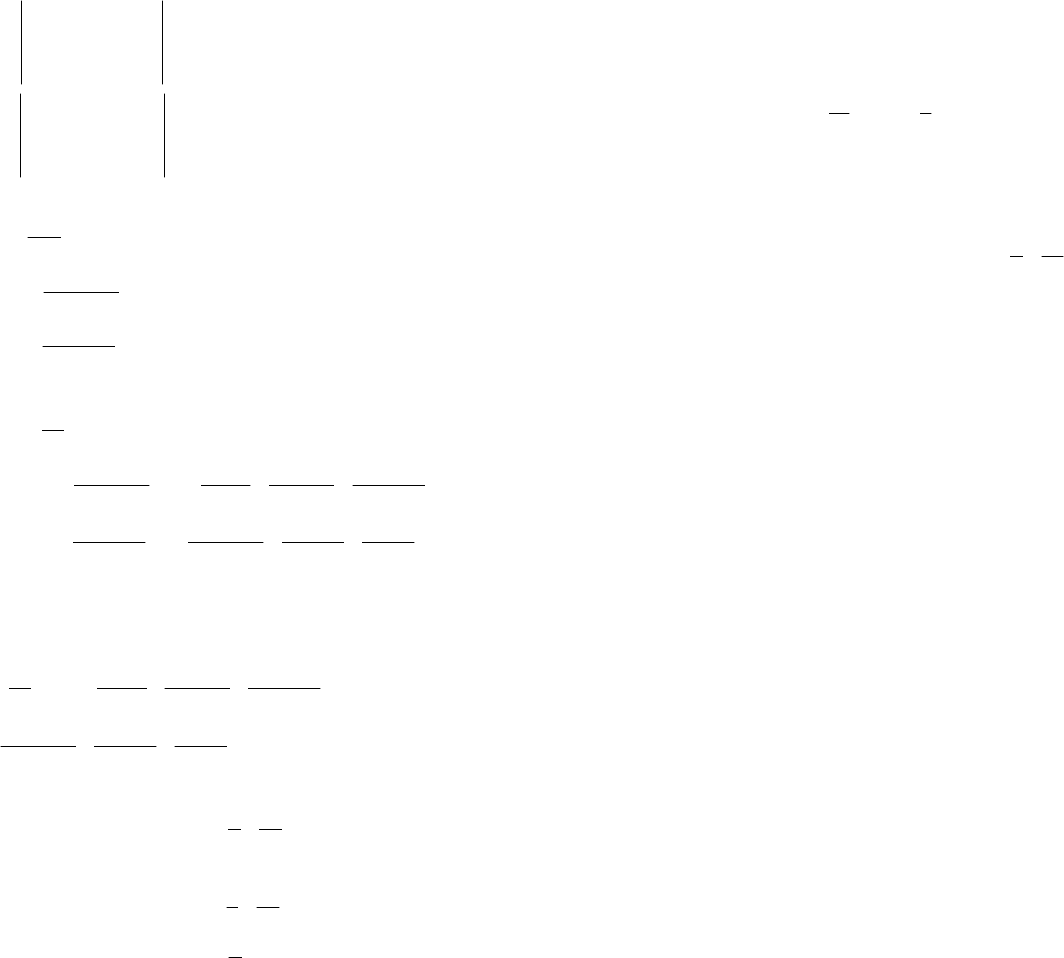
221
2
2
2
10sin2
002cos22cos2,
04sin2
x
xxx
xx
∆==−
−
2
3
2
1cos20
02sin202sin2.
04cos2
x
xxx
xx
∆=−=−
−
Тогда решение системы:
2
1
2
2
2
3
2
,
8
cos2
,
4
sin2
.
4
x
C
xx
C
xx
C
′
=
′
=−
′
=−
Интегрируем эти равенства:
3
11
(),
12
x
CxC
=+
22
22
cos2sin2cos2sin2
(),
41688
xxxxxxx
CxdxC
=−=−−+
∫
22
33
sin2cos2sin2cos2
(),
48816
xxxxxxx
CxdxC
=−=−−+
∫
где
123
,,
CCC
– произвольные постоянные (при интегрировании
2
C
′
и
3
C
′
применялся метод интегрирования по частям).
Подставляя выражения для
123
,,
CCC
в общее решение, получаем:
32
12
sin2cos2sin2
cos2
121688
xxxxxx
yCCx
=++−−++
2
3
cos2sin2cos2
sin2
8816
xxxxx
Cx
+−−+
или после упрощения:
3
123
cos2sin2.
812
xx
yCCxCx=++−+
Дифференцируем полученное общее решение дважды:
2
23
1
2sin22cos2,
84
x
yCxCx
′
=−+−+
23
4cos24sin2.
2
x
yCxCx
′′
=−−+
222
Подставляем в выражения для
,,
yyy
′′′
заданные начальные усло-
вия и находим
123
,,:
CCC
12
3
2
2,
151
2,
88
44.
CC
C
C
=+
=−
=−
Отсюда
1
3,
C
=
2
1,
C
=−
3
1.
C
=
Получили решение задачи Коши:
3
3cos2sin2.
812
xx
yxx=−+−+
Пример 3. Решить уравнение:
1)
32
3(2);
x
yyex
−
′′′
−=+ 2)
22cos3sin;
IV
yyyxx
′′
++=+
3)
44(cos2sin2).
x
yyyyexxx
−
′′′′′′
+++=+
Решение. 1) Это линейное неоднородное дифференциальное урав-
нение 2-го порядка с постоянными коэффициентами и правой частью
специального вида. Для его решения используем метод Эйлера.
Рассмотрим соответствующее однородное уравнение
30.
yy
′′′
−=
Его характеристическое уравнение
2
30,
λλ
−=
корни которого
1
0,
λ
=
2
3
λ
=
– действительные, простые.
Тогда общее решение соответствующего однородного уравнения:
3
012
,
x
yCCe
=+ где
12
,
CC
– произвольные постоянные. Запишем
контрольное число
3
σ
=−
(так как
3,
α
=−
0
β
=
). Контрольное число
не содержится среди корней характеристического уравнения. Тогда ис-
комое частное решение заданного дифференциального уравнения име-
ет вид:
32
(),
x
ч
yeAxBxC
−
=++
где A, B, C – неопределенные коэффициенты, которые надо найти.
Вычислим производные
,:
÷÷
yy
′′′
323
3()(2),
xx
ч
yeAxBxCeAxB
−−
′
=−++++
32333
9()3(2)3(2)2.
xxxx
ч
yeAxBxCeAxBeAxB Аe
−−−−
′′
=++−+−++
Подставляем полученные выражения
ч
y
′
и
ч
y
′′
в заданное диффе-
ренциальное уравнение:
3233
9()6(2)2
xxx
eAxBxCeAxB Аe
−−−
++−++−
32332
3(3()(2))(2).
xxx
eAxBxCeAxBex
−−−
−−++++=+
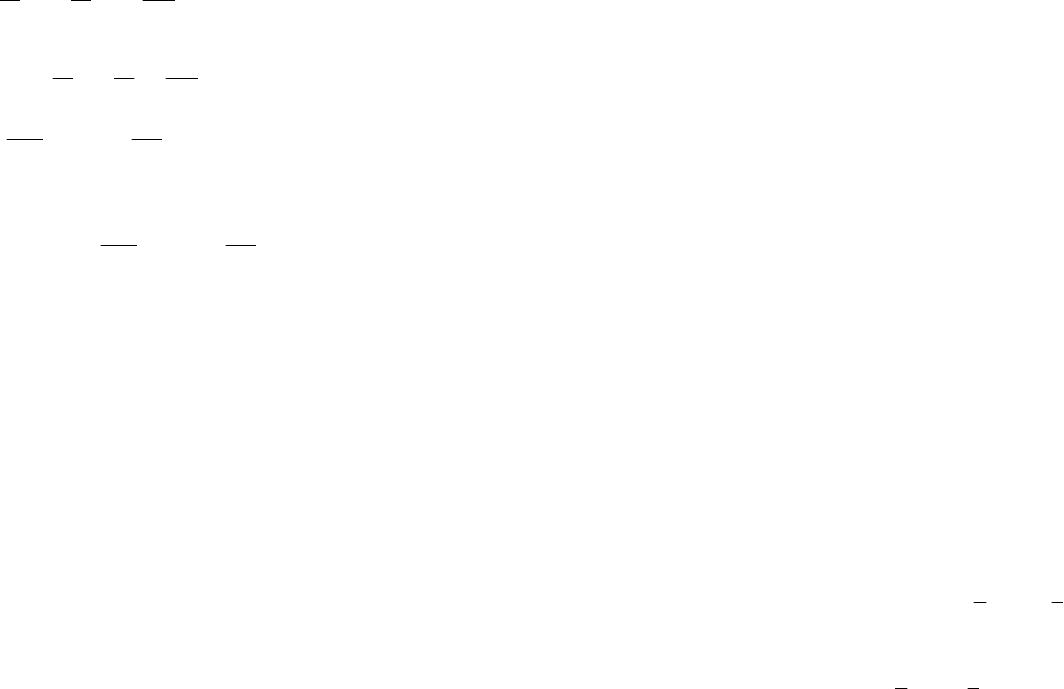
223
Сокращаем на
3
x
e
−
и группируем относительно степеней x:
2
2
(99)(91296)96293
44.
ААxBABAxCBACB
xx
++−+−+−++−=
=++
Приравниваем коэффициенты при одинаковых степенях x:
2
1
0
:
181,
:18184,
18924.
:
x
A
xBA
CBA
x
=
−=
−+=
Решаем полученную систему уравнений и находим A, B, C:
15115
,,.
1818324
ABC===
Подставляем найденные коэффициенты в частное решение:
32
15115
1818324
x
ч
yexx
−
=++
или
3
2
115
5.
1818
x
ч
e
yxx
−
=++
Тогда общее решение заданного дифференциального уравнения
имеет вид:
3
32
12
115
5.
1818
x
x
e
yCCexx
−
=++++
2) Это линейное неоднородное дифференциальное уравнение 4-го
порядка с постоянными коэффициентами и правой частью специально-
го вида. Используем метод Эйлера для нахождения его общего реше-
ния. Соответствующее однородное уравнение –
20.
IV
yyy
′′
++=
Его
характеристическое уравнение
42
210
λλ
++=
или
22
(1)0,
λ
+=
корни которого
1,2
i
λ
=±
кратности 2 (комплексно-сопряженные).
Тогда общее решение соответствующего однородного уравнения:
01234
coscossinsin,
yCxCxxCxCxx
=+++
где
1234
,,,
CCCC
– произвольные постоянные.
Запишем контрольное число
,
i
σ
=
так как
0,
α
=
1.
β
=
Кон-
трольное число
σ
содержится среди корней характеристического
уравнения кратности 2. Поэтому искомое частное решение заданного
дифференциального уравнения ищем в виде
2
(cossin),
ч
yxAxBx
=+
где A, B – коэффициенты, которые надо найти.
Дифференцируем
ч
y
дважды:
224
2
2(cossin)(sincos),
ч
yxAxBxxAxBx
′
=++−+
2
2(cossin)2(sincos)
2(sincos)(cossin).
ч
yAxBxxAxBx
xAxBxxAxBx
′′
=++−++
+−++−−
Упростим
:
ч
y
′′
2
(2)(cossin)4(sincos).
ч
yxAxBxxAxBx
′′
=−++−+
Далее получим:
2
2(cossin)(2)(sincos)
ч
yxAxBxxAxBx
′′′
=−++−−++
4(sincos)4(cossin).
AxBxxAxBx
+−++−−
Упростим это выражение:
2
6(cossin)(6)(sincos).
ч
yxAxBxxAxBx
′′′
=−++−−+
Дифференцируем еще раз:
6(cossin)6(sincos)
IV
ч
yAxBxxAxBx
=−+−−+−
2
2(sincos)(6)(cossin).
xAxBxxAxBx
−−++−−−
Упрощаем это выражение:
2
(12)(cossin)8(sincos).
IV
ч
yxAxBxxAxBx
=−+−−+
Подставляем выражения для
,
IV
ч
y
ч
y
′′
и
ч
y
в заданное дифферен-
циальное уравнение:
2
(12)(cossin)8(sincos)
xAxBxxAxBx
−+−−++
2
2(2)(cossin)8(sincos)
xAxBxxAxBx
+−++−++
2
(cossin)2cos3sin.
xAxBxxx
++=+
Группируем относительно
cos
x
и
sin:
x
222
(128428)cos
AxABxAAxBxAxx
−−+−+++
222
(128428)sin2cos3sin.
BxBAxBBxAxBxxxx
+−++−−+=+
После преобразований в скобках получим:
8cos8sin2cos3sin.
А xBxxx
−−=+
Приравниваем коэффициенты при одноименных тригонометриче-
ских функциях и получаем систему
cos:82,
sin:83,
xA
xB
−=
−=
решение которой:
13
,.
48
AB
=−=−
Подставляем найденные коэффициенты в частное решение
:
ч
y
2
13
cossin.
48
ч
yxxx
=−−

225
Тогда общее решение заданного дифференциального уравнения:
2
1234
13
coscossinsincossin
48
yCxCxxCxCxxxxx
=++++−−
или
22
1234
3
cossin.
48
xx
yCCxxCCxx
=+−++−
3) Это линейное неоднородное дифференциальное уравнение 3-го
порядка с постоянными коэффициентами и специальной правой ча-
стью. Соответствующее однородное уравнение –
440.
yyyy
′′′′′′
+++=
Его характеристическое уравнение
32
440
λλλ
+++=
или
2
(1)(4)0.
λλ
++=
Получаем корни характеристического уравнения
1
1,
λ
=−
2,3
2.
i
λ
=±
Общее решение соответствующего однородного уравнения имеет
вид:
0123
cos2sin2,
x
yCeCxCx
−
=++
где
123
,,
CCC
– произвольные постоянные.
Запишем контрольное число
12,
i
σ
=−+
так как
1,
α
=−
2.
β
=
Контрольное число не содержится среди корней характеристического
уравнения. Тогда искомое частное решение заданного дифференциаль-
ного уравнения ищем в виде
(()cos2()sin2),
x
ч
yeAxBxCxDx
−
=+++
где A, B, C, D – коэффициенты, которые надо найти. Дифференци-
руем трижды
:
ч
y
(()cos2()sin2)
x
ч
yeAxBxCxDx
−
′
=−++++
(cos22()sin2sin22()cos2).
x
eAxAxBxCxCxDx
−
+−++++
Упростим это выражение:
((22)cos2(22)sin2).
x
ч
yeAxCxBADxCxAxDBCx
−
′
=−+−+++−−−−+
Далее дифференцируем:
((22)cos2(2
x
ч
yeAxCxBADxCxAxD
−
′′
=−−+−+++−−−−
2)sin2)((2)cos22(2
x
BCxeACxAxCxB
−
−++−+−−+−+
2)sin2(2)sin22(22)cos2).
ADxCAxCxAxDBCx
+++−−+−−−−+
Упростим это выражение:
((342344)cos2(434
x
ч
yeAxCxABCDxAxCxA
−
′′
=−−−−+−+−−+
423)sin2.
BCDx
+−−
((342344)cos2(434
x
ч
yeAxCxABCDxAxCxA
−
′′′
=−−−−−+−+−−+
226
423)sin2)((34)cos22(342
x
BCDxeACxAxCxA
−
+−−+−−−−−−−
344)sin2(43)sin22(4344
23)cos2).
BCDxACxAxCxAB
CDx
−+−+−+−−+−
−−
Упростим это выражение:
((112911122)cos2(2
x
ч
yeAxCxABCDxAx
−
′′′
=−−+−−++
11122911)sin2).
CxABCDx
+++−+
Подставляя выражения для
,,,
чччч
yyyy
′′′′′′
в заданное дифферен-
циальное уравнение, группируем и, приравнивая коэффициенты при
одноименных тригонометрических функциях, имеем:
cos2:112344840,
sin2:211438441,
cos2:911122234444841,
sin2:122911442348440.
xxACACACA
xxACACACC
xABCDABCDBADB
xABCDABCDDBCD
−−−−++=
++−−−+=
−+−−−−+−−+++=
+−+−+−−−−++=
Упрощая выражения, получаем систему уравнений
820,
281,
78821,
82780.
AC
AC
ABCD
ABCD
+=
−+=
−+−+=
−−+=
Решаем ее и находим:
1450203
,,,.
34342891156
ACBD=−===
Подставляем найденные коэффициенты в
÷
y
504203
cos2sin2.
28934341156
x
ч
xx
yexx
−
=−++
Тогда общее решение заданного дифференциального уравнения:
123
cos2sin2
x
yCeCxCx
−
=+++
504203
cos2sin2.
28934341156
x
xx
exx
−
+−++
Пример 4. Решить уравнения:
1)
2
23;
x
yyye
′′′
−−= 2)
25cos5;
yyx
′′
+= 3)
2.
x
yyxe
′′
−=+
Решение. 1) Это линейное неоднородное уравнение 2-го порядка с
постоянными коэффициентами и специальной правой частью вида
2
()(0cos0sin0),
x
fxexbx
=⋅+⋅
где b – число,
2,
α
=
0.
β
=
Соответствующее однородное уравнение:

227
230.
yyy
′′′
−−=
Его характеристическое уравнение
2
230,
λλ
−−=
корни которого
1
1,
λ
=−
2
3
λ
=
– действительные, простые.
Тогда общее решение соответствующего однородного дифферен-
циального уравнения:
3
012
.
xx
yCeCe
−
=+
Запишем контрольное число
2.
σ
=
Оно не является корнем харак-
теристического уравнения.
Тогда частное решение заданного дифференциального уравнения
ищем в виде
2
,
x
ч
yAe
=
где A – коэффициент, который надо найти.
Дифференцируем
ч
y
дважды:
2
2,
x
ч
yAe
′
=
2
4.
x
ч
yAe
′′
=
Подставляем
,,
ччч
yyy
′′′
в заданное дифференциальное уравнение:
2222
4223,
xxxx
AeAeAee
−⋅−=
получаем
1
.
3
A
=−
Затем подставляем этот коэффициент в выражение для
:
ч
y
2
.
3
x
ч
e
y =−
Общее решение заданного дифференциального уравнения запи-
шем в виде
2
3
12
.
3
x
xx
e
yCeCe
−
=+−
2) Это линейное неоднородное дифференциальное уравнение 2-го
порядка с постоянными коэффициентами и специальной правой ча-
стью вида
0
()(1cos50sin5),
x
fxexx
=⋅+⋅ где
0,
α
=
5.
β
=
Соответствующее однородное уравнение имеет вид:
250.
yy
′′
+=
Его характеристическое уравнение
2
250,
λ
+=
корни которого
1,2
5
i
λ
=±
– простые комплексно-сопряженные.
Тогда общее решение однородного уравнения:
012
cos5sin5.
yCxCx
=+
228
Контрольное число
5
i
σ
=
совпадает с одним из корней характе-
ристического уравнения, кратности 1. Поэтому частное решение за-
данного дифференциального уравнения ищем в виде
(cos5sin5),
ч
yxAxBx
=+
где A, B – коэффициенты, которые надо найти.
Дифференцируем
ч
y
дважды:
(cos5sin5)(5sin55cos5),
ч
yAxBxxAxBx
′
=++−+
5sin55cos55sin55cos5
ч
yAxBxAxBx
′′
=−+−++
(25cos525sin5).
xAxBx
+−−
Упрощаем
:
ч
y
′′
10sin510cos5(25cos525sin5).
ч
yAxBxxAxBx
′′
=−++−−
Подставляем
,
чч
yy
′′
в заданное дифференциальное уравнение:
10sin510cos5(25cos525sin5)
AxBxxAxBx
−++−−+
25(cos5sin5)cos5.
xAxBxx
++=
Группируя относительно
sin5,
x
а также
cos5
x
и приравнивая ко-
эффициенты при одноименных тригонометрических функциях, полу-
чим систему
{
101,
100,
B
A
=
−=
из которой находим
1
0,.
10
AB==
Тогда частное решение:
sin5,
10
ч
x
yx
=
а общее решение заданного дифференциального уравнения:
12
cos5sin5sin5
10
x
yCxCxx
=++ или
12
cos5sin5.
10
x
yCxCx
=++
3) Это линейное неоднородное дифференциальное уравнение с по-
стоянными коэффициентами и специальной правой частью вида
12
()()2.
x
fxfxxe
+=+
Для нахождения его общего решения воспользу-
емся методом Эйлера и теоремой о наложении решений.
Соответствующее однородное уравнение для заданного диффе-
ренциального уравнения
0.
yy
′′
−=
Его характеристическое уравнение
2
10,
λ
−=
корни которого
1,2
1
λ
=±
– простые действительные.
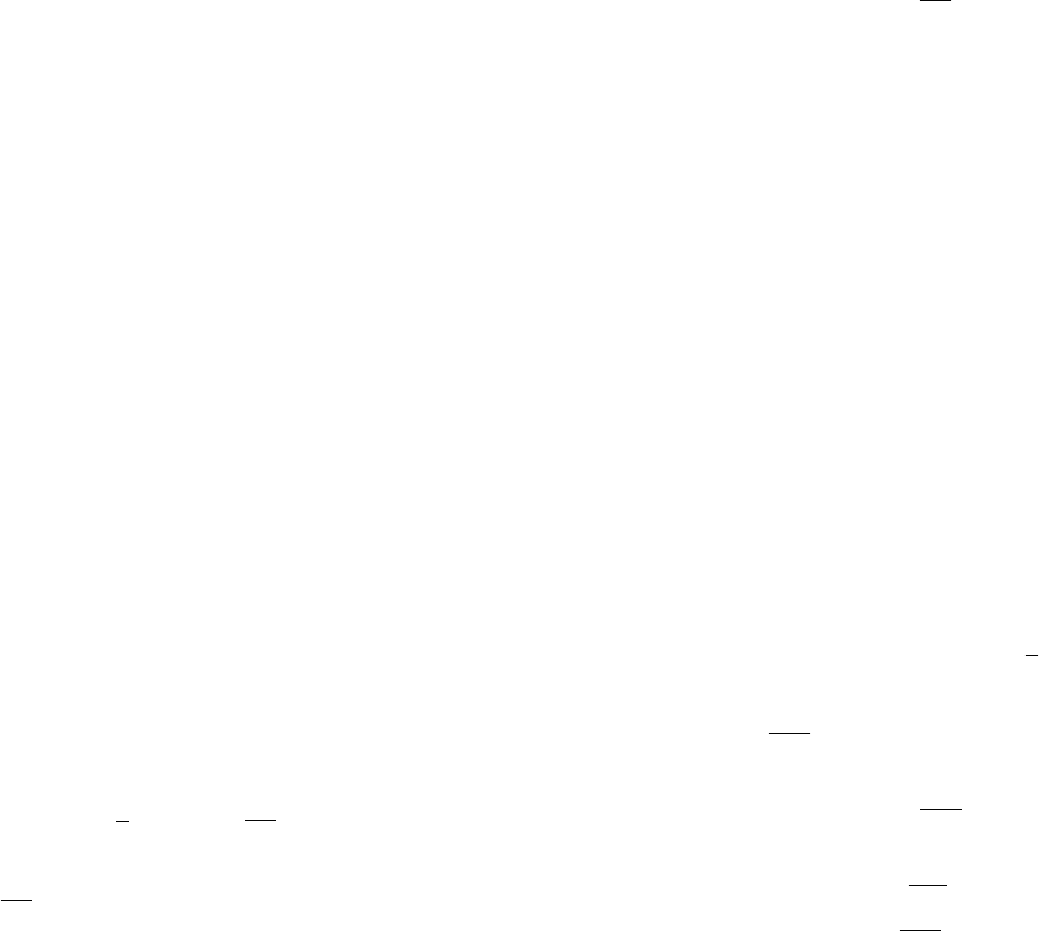
229
Общее решение однородного уравнения:
012
.
xx
yCeCe
−
=+
Частное решение заданного дифференциального уравнения будем
искать в виде
12
,
ччч
yyy
=+
где
1
ч
y
– частное решение дифференциального уравнения:
2;
yyx
′′
−= (22.71)
2
ч
y
– частное решение дифференциального уравнения:
.
x
yye
′′
−= (22.72)
Контрольные числа этих дифференциальных уравнений
1
0
σ
=
и
2
1,
σ
=
соответственно. Заметим, что
1
0
σ
=
не является корнем харак-
теристического уравнения, значит, частное решение
1
ч
y
ищем в виде
1
,
ч
yAxB
=+
где A, B – коэффициенты, которые надо найти.
Дифференцируем
1
:
ч
y
1
,
ч
yA
′
=
1
0.
ч
y
′′
=
Подставляя в дифференциальное уравнение (22.71)
1
ч
y
′′
и
1
,
ч
y
получим:
2,
AxBx
−−=
откуда находим
2,
A
=−
0.
B
=
Тогда
1
2.
ч
yx
=−
Аналогично, так как
2
1
σ
=
– простой корень характеристического
уравнения, то частное решение (22.72) ищем в виде
2
,
x
ч
yCxe
=
где С – коэффициент, который надо найти.
Дифференцируем
2
:
ч
y
2
,
xx
ч
yCeCxe
′
=+
2
2.
xx
ч
yCeCxe
′′
=+
Подставляем
2
ч
y
′′
и
2
ч
y
в (22.72):
2
xxxx
CeCxeCxee
+−=
или
2.
xx
Cee
=
Отсюда получаем, что
1
.
2
C
=
Тогда
2
.
2
x
ч
xe
y =
Записываем частное решение заданного дифференциального урав-
нения:
2.
2
x
ч
xe
yx=−+ Тогда общее решение заданного дифференци-
ального уравнения имеет вид:
230
12
2.
2
x
xx
xe
yCeCex
−
=+−+
Пример 5. Решить задачу Коши:
sin,
yyx
′′′′
−=
(0)2,5,
y =
(0)0,
y
′
=
(0)1,5.
y
′′
=
Решение. Это линейное неоднородное дифференциальное уравне-
ние с постоянными коэффициентами и специальной правой частью вида
0
()(0cos1sin),
x
fxexx
=⋅+⋅
где
0,
α
=
1,
β
=
()0,
Px
=
()1.
Qx
=
Соответствующее однородное дифференциальное уравнение
0.
yy
′′′′
−=
Его характеристическое уравнение:
3
0,
λλ
−=
корни кото-
рого
1
0,
λ
=
2,3
1
λ
=±
– действительные, простые. Тогда общее реше-
ние однородного уравнения:
0123
.
xx
yCCeCe
−
=++
Контрольное число
i
σ
=
не является корнем характеристического
уравнения. Поэтому частное решение заданного дифференциального
уравнения ищем в виде
cossin,
ч
yAxBx
=+
где A, B – неизвестные коэффициенты.
Дифференцируем
ч
y
трижды:
sincos,
ч
yAxBx
′
=−+
cossin,
ч
yAxBx
′′
=−−
sincos.
ч
yAxBx
′′′
=−
Подставляем
ч
y
′′′
и
ч
y
′
в заданное дифференциальное уравнение:
sincos(sincos)sin.
AxBxAxBxx
−−−+=
Приравниваем коэффициенты при одноименных тригонометриче-
ских функциях, получаем систему
{
21,
20,
A
B
=
−=
из которой находим
1
,0.
2
AB
==
Тогда получаем:
cos
.
2
ч
x
y =
Общее решение заданного дифференциального уравнения:
123
cos
.
2
xx
x
yCCeCe
−
=+++
Дифференцируем общее решение:
23
23
sin
,
2
cos
.
2
xx
xx
x
yCeCe
x
yCeCe
−
−
′
=−+−
′′
=+−
231
Подставляем заданные начальные условия:
123
23
23
51
,
22
0,
31
.
22
CCC
CC
CC
=+++
=−+
=+−
Из полученной системы находим
123
0,1,1.
CCC
===
Решением задачи Коши является
cos
.
2
xx
x
yee
−
=++
Задания
I уровень
1.1. Решите уравнение:
1)
;
yyx
′′
−=
2)
76cos;
yyyx
′′′
−+=
3)
32;
yyx
′′′
+=−
4)
2sin.
yyx
′′
+=
1.2. Решите задачу Коши:
1)
5
43,
x
yyye
−
′′′
−+=
1
(0),
48
y =
43
(0);
48
y
′
=
2)
24,
yy
′′′
−=
(0)2,
y
=
(0)0;
y
′
=
3)
,
yyx
′′′′
+=
(0)4,
y
=
(0)3,
y
′
=
(0)1.
y
′′
=−
1.3. Найдите общее решение уравнения методом Лагранжа:
1)
1
4;
cos2
yy
x
′′
+= 2)
.
yyx
′′
−=
II уровень
2.1. Найдите общее решение уравнения методом Лагранжа:
1)
4tg2;
yyx
′′
+=
2)
2
44;
x
e
yyy
x
′′′
−+=
3)
2
cos
;
sin
x
yy
x
′′′′
+= 4)
3
1
4.
cos2
yy
x
′′
−=
2.2. Решите уравнение:
1)
22;
VIV
yyyx
′′′
−−= 2)
4sin2cos;
yyxx
′′
−=−
3)
sin2sin;
yyxx
′′
+=+
4)
3
324.
x
yyxe
′′′
−=−
232
2.3. Решите задачу Коши:
1)
2
,
yyx
′′
−=
(0)2,
y
=−
(0)4;
y
′
=
2)
2sin,
x
yyyex
′′′
−+=
(0)1,
y
=
(0)2;
y
′
=
3)
9cos3,
yyx
′′
+=
(0)1,
y
=
(0)3;
y
′
=
4)
2
,
xx
yyxee
′′
−=+
1
(0),
4
y
=
1
(0).
2
y
′
=
2.4. Укажите вид частного решения дифференциального
уравнения:
1)
2
2cos;
IV
yyyyyxx
′′′′′′
−−−−= 2)
2
325;
yiyxix
′′′′′
−=−+
3)
3sin25cos2;
yyxxx
′′′′′
−=+
4)
3
10922.
Vxx
yyyxee
−
′′′′
−+=+
III уровень
3.1. Решите уравнение:
1)
2
sin;
x
yyxex
′′′′′
−=++ 2)
3
3cos;
x
yyex
′′
−=+
3)
2(cos);
x
yyyexx
−
′′′
++=+ 4)
2sinsin2.
yyxx
′′
+=
3.2. Найдите общее решение методом Лагранжа:
1)
22
1;
xx
yyee
′′
−=− 2)
2
2
962
69;
xx
yyy
x
++
′′′
−+=
3)
2
41
;
x
yy
xx
+
′′
−= 4)
2
3
22
2.
xx
yyy
x
++
′′′
−+=
22.8. Системы дифференциальных уравнений
Система дифференциальных уравнений вида
( )
( )
( )
1
112
2
212
12
,,,,,
,,,,,
........................................
....
,,,,,
n
n
n
nn
dy
dx
dy
dx
dy
dx
fxyyy
fxyyy
fxyyy
=
=
=
K
K
K
(22.73)
где
12
,,...,
n
yyy
– искомые функции переменной x, называ-

233
ется нормальной системой.
Совокупность n функций
12
,,...,,
n
yyy
удовлетворяющих
каждому уравнению системы (22.73), называется решением этой
системы.
Задача Коши для системы (22.73) состоит в нахождении
решения этой системы, удовлетворяющего начальным услови-
ям:
0
101
(),
yxy
=
0
202
(),
yxy
= …,
0
0
().
nn
yxy
=
Основные методы интегрирования нормальных систем (22.73) –
метод исключения и метод интегрируемых комбинаций.
Метод исключения
Этот метод позволяет свести нормальную систему из n ли-
нейный дифференциальных уравнений к одному линейному
дифференциальному уравнению n-го порядка относительно од-
ной неизвестной функции.
Метод интегрируемых комбинаций
Метод заключается в том, что посредством арифметических
операций из уравнений системы (22.73) получают легко интег-
рируемые уравнения относительно новой неизвестной функции.
Пример 1. Решить систему:
1)
2
sin,
;
2
dy
zx
dx
dzy
dxz
=+
=
2)
1
12
2
21
2,
4;
dy
yy
dx
dy
yy
dx
=+
=−
3)
1
32
2
3
3
31
,
,
.
dy
yy
dx
dy
y
dx
dy
yy
dx
=−
=
=−
Решение. 1) Используем метод исключения. Дифференцируем
первое уравнение системы по x:
2
2
2cos.
dydz
zx
dx
dx
=+
Подставив в полученное уравнение из второго уравнения системы
выражение вместо
,
dz
dx
имеем:
2
2
2cos
2
dyy
zx
z
dx
=+ или
2
2
cos.
dy
yx
dx
−= (22.74)
Последнее уравнение – линейное неоднородное дифференциаль-
234
ное уравнение 2-го порядка со специальной правой частью. Его соот-
ветствующее однородное уравнение:
0.
yy
′′
−=
Характеристическое уравнение последнего:
2
10,
λ
−=
корни которого
1,2
1.
λ
=±
Тогда общее решение одно-
родного уравнения:
012
.
xx
yCeCe
−
=+
Ищем частное решение полученного неоднородного уравнения
(22.74) в виде
cossin,
ч
yAxBx
=+
где A, B – неопределенные коэффициенты.
Вычисляем производные:
sincos,
ч
yAxBx
′
=−+
cossin.
ч
yAxBx
′′
=−−
Подставляем их в уравнение (22.74), группируем относительно
sin x и cos x, приравниваем коэффициенты.
Получаем систему
{
21,
20,
A
B
−=
−=
из которой находим
1
,0.
2
АВ
=−=
Общее решение дифференциального уравнения 2-го порядка:
12
cos
.
2
xx
x
yCeCe
−
=+− (22.75)
Возвращаемся к первому уравнению заданной системы, из которо-
го выражаем
2
:
z
2
sin.
dy
zx
dx
=−
Подставляя в это уравнение продифференцированное общее ре-
шение (22.75), получим:
2
21
sin
.
2
xx
x
zCeCe
−
=−− (22.76)
Функции (22.75) и (22.76) составляют общее решение заданной
системы.
2) Применим метод исключения. Выразим из первого уравнения
системы
2
:
y
1
21
2.
dy
yy
dx
=−
Отсюда, дифференцируя по x, получим:
2
211
2
2.
dydydy
dxdx
dx
=−
235
Подставим правую часть полученного равенства вместо
2
dy
dx
во
второе уравнение системы:
2
111
11
2
248
dydydy
yy
dxdx
dx
−=−−
или
111
690.
yyy
′′′
−+=
Получили однородное дифференциальное уравнение 2-го порядка
с постоянными коэффициентами. Его характеристическое уравнение:
2
690;
λλ
−+=
решая которое, находим:
3
λ
=
– корень кратности 2.
Тогда
33
112
().
xx
yxCeCxe
=+
Продифференцируем функцию
1
:
y
33
1
12
3(31).
xx
dy
CeCex
dx
=++
Возвращаясь к первому уравнению системы, имеем:
3333
21212
()3(31)2().
xxxx
yxCeCexCeCxe=++−+
Упрощаем:
333
2122
().
xxx
yxCeCxeCe
=++
Таким образом, получаем общее решение заданной системы:
3
112
3
2122
()(),
()().
x
x
yxeCCx
yxeCCxC
=+
=++
3) Используем метод исключения. Дифференцируем первое урав-
нение системы:
2
3
12
2
.
dy
dydy
dxdx
dx
=−
Подставив в него выражения для
3
dy
dx
и
2
dy
dx
из 2-го и 3-го урав-
нений системы, получим линейное однородное дифференциальное
уравнение 2-го порядка:
2
1
1
2
0.
dy
y
dx
+=
Его характеристическое урав-
нение имеет вид:
2
10,
λ
+=
корни которого
1,2
i
λ
=±
– простые ком-
плексно-сопряженные. Тогда общим решением однородного диффе-
ренциального уравнения будет:
112
()cossin.
yxCxCx
=+
Из третьего уравнения системы получаем:
3
31
.
dy
yy
dx
−=−
236
Подставим в него найденное выражение для
1
,
y
получим линей-
ное неоднородное дифференциальное уравнение 1-го порядка:
3
312
cossin.
dy
yCxCx
dx
−=−− (22.77)
Решим его методом Эйлера. Характеристическое уравнение соот-
ветствующего однородного
10,
λ
−=
корень которого
1.
λ
=
Тогда
общее решение соответствующего однородного:
0
33
.
x
yCe
=
Частное решение неоднородного дифференциального уравнения
ищем в виде
3
cossin,
ч
yAxBx
=+
где A, B – неопределенные коэффициенты.
Вычисляем
3
sincos
ч
yAxBx
′
=−+ и подставляем в неоднородное
уравнение (22.77).
Для определения A и B приходим к системе
{
1
2
,
,
BAC
BAC
−=−
−−=−
из которой находим
1221
,.
22
ÑÑÑÑ
ÀÂ
+−
==
Тогда получаем:
()
1221
33
cossin.
22
x
CCCC
yxCexx
+−
=++
Из первого уравнения заданной системы выразим
2
:
y
1
23
.
dy
yy
dx
=−
Подставим в это равенство найденные
3
y
и
1
,
dy
dx
получим:
()
1212
23
cossin.
22
x
CCCC
yxCexx
−+
=++
Таким образом, получено решение заданной системы дифферен-
циальных уравнений:
(
)
()
()
112
1212
23
1221
33
cossin,
cossin,
22
cossin.
22
x
x
yxCxCx
CCCC
yxCexx
CCCC
yxCexx
=+
−+
=++
+−
=++
