Майсеня Л.И. Математика в примерах и задачах. Часть 4
Подождите немного. Документ загружается.

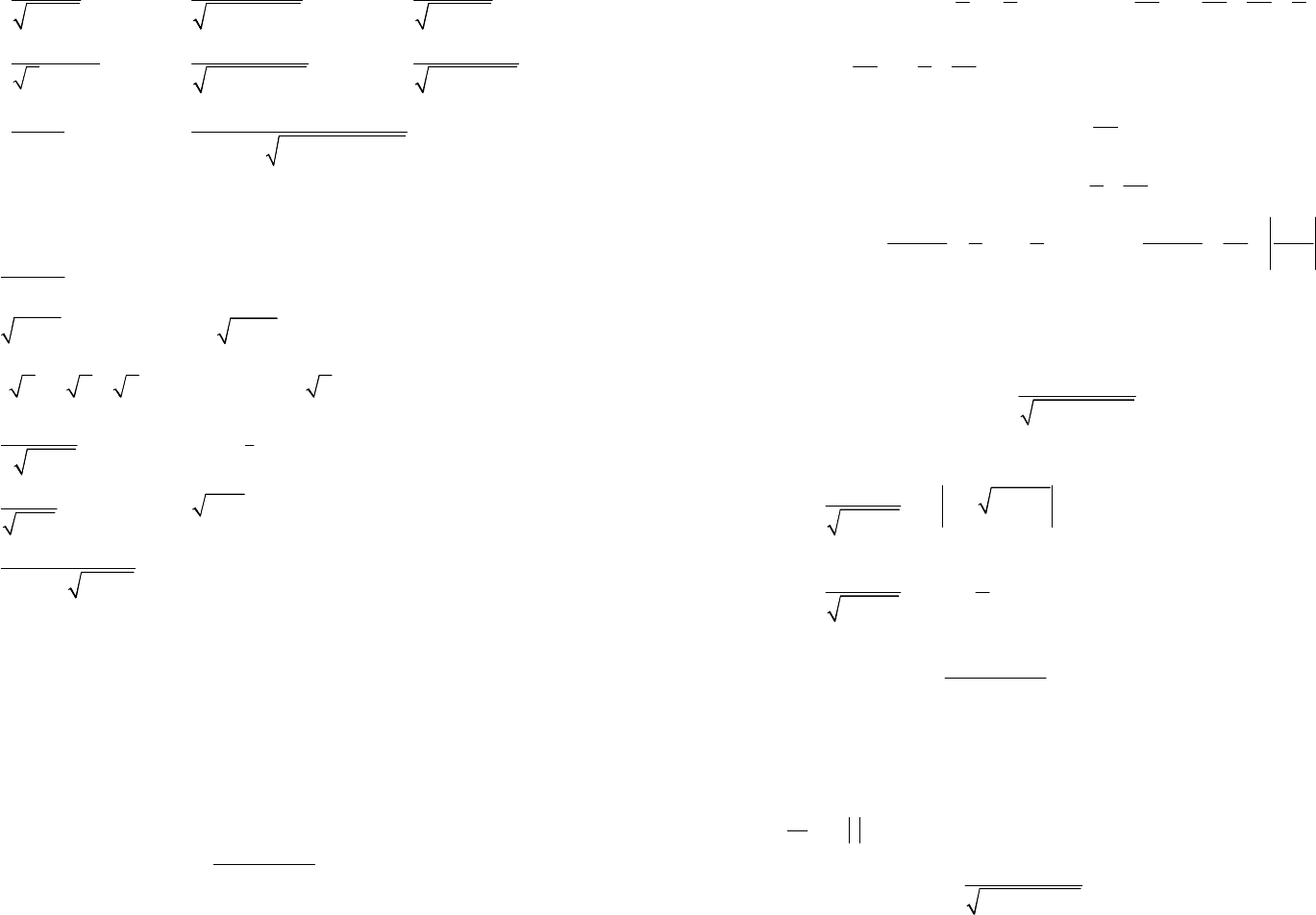
19
7)
3
2
sin
;
cos
xdx
x
∫
8)
2
sin
;
82cos
x
dx
x−
∫
9)
2
6
;
94
xdx
x
−
∫
10)
( )
;
9
dx
xx
+
∫
11)
4
sin2
;
169sin
xdx
x
−
∫
12)
42
;
1
xdx
xx
−−
∫
13)
3
4
;
1
xx
dx
x
+
+
∫
14)
22
.
(14)259arctg2
dx
xx
+−
∫
3.2. Найдите неопределенный интеграл методом подстанов-
ки или методом замены переменной:
1)
5
4
1
(1)
x
dx
x
+
−
∫
(у к а з а н и е:
1);
xt
−=
2)
1
x
edx
−
∫
(у к а з а н и е:
1);
x
et
−=
3)
( )
36
2
xxxdx
−+
∫
(у к а з а н и е:
6
);
xt
=
4)
2
1
dx
xx
−
∫
(у к а з а н и е:
1
);
x
t
=
5)
3
1
xdx
x
+
∫
(у к а з а н и е:
3
1);
xt
+=
6)
22
(4)4
dx
xx
−−
∫
(у к а з а н и е:
2sin).
xt
=
19.3. Интегрирование некоторых выражений,
содержащих квадратный трехчлен
2
ax+bx+c
Рассмотрим некоторые виды интегралов, содержащих квад-
ратный трехчлен в подынтегральном выражении, и способы их
вычисления. Всюду далее считаем
,,0.
abc
≠
Для вычисления интеграла вида
2
dx
axbxc
++
∫
(19.17)
выделим полный квадрат в квадратном трехчлене:
20
22
222
2
244
bcbbbc
axbxcaxxaxx
aaaaaa
++=++=+⋅⋅+−+=
2
2
.
24
bcb
ax
aaa
=++−
Сделаем замену переменной
.
2
b
xt
a
+=
Тогда интеграл (19.17),
в зависимости от знака выражения
2
,
4
cb
aa
− сводится к одному из
интегралов
22
1
arctg
dtt
C
kk
tk
=+
+
∫
или
22
1
ln.
2
dttk
C
ktk
tk
−
=+
+
−
∫
Вместо замены переменной (после выделения полного квад-
рата) можно использовать также метод поднесения под знак
дифференциала.
Интеграл вида
2
dx
axbxc
++
∫
(19.18)
также вычисляется выделением полного квадрата в квадратном
трехчлене. Он сводится к интегралу
22
22
ln,
dt
ttkC
tk
=+±+
±
∫
если
0,
a
>
или к интегралу
22
arcsin,
dtt
C
k
kt
=+
−
∫
если
0.
a
<
Рассмотрим интеграл вида
2
,
MxN
dx
axbxc
+
++
∫
где
0.
M
≠
(19.19)
В числителе подынтегральной функции выделяем произ-
водную
2
axb
+
квадратного трехчлена, записанного в знамена-
теле. Тогда интеграл (19.19) можно представить в виде суммы
двух интегралов, один из которых сводится к интегралу
ln,
dt
tC
t
=+
∫
а второй вычисляем как интеграл вида (19.17).
Интеграл вида
2
MxN
dx
axbxc
+
++
∫
сводится к сумме интегра-
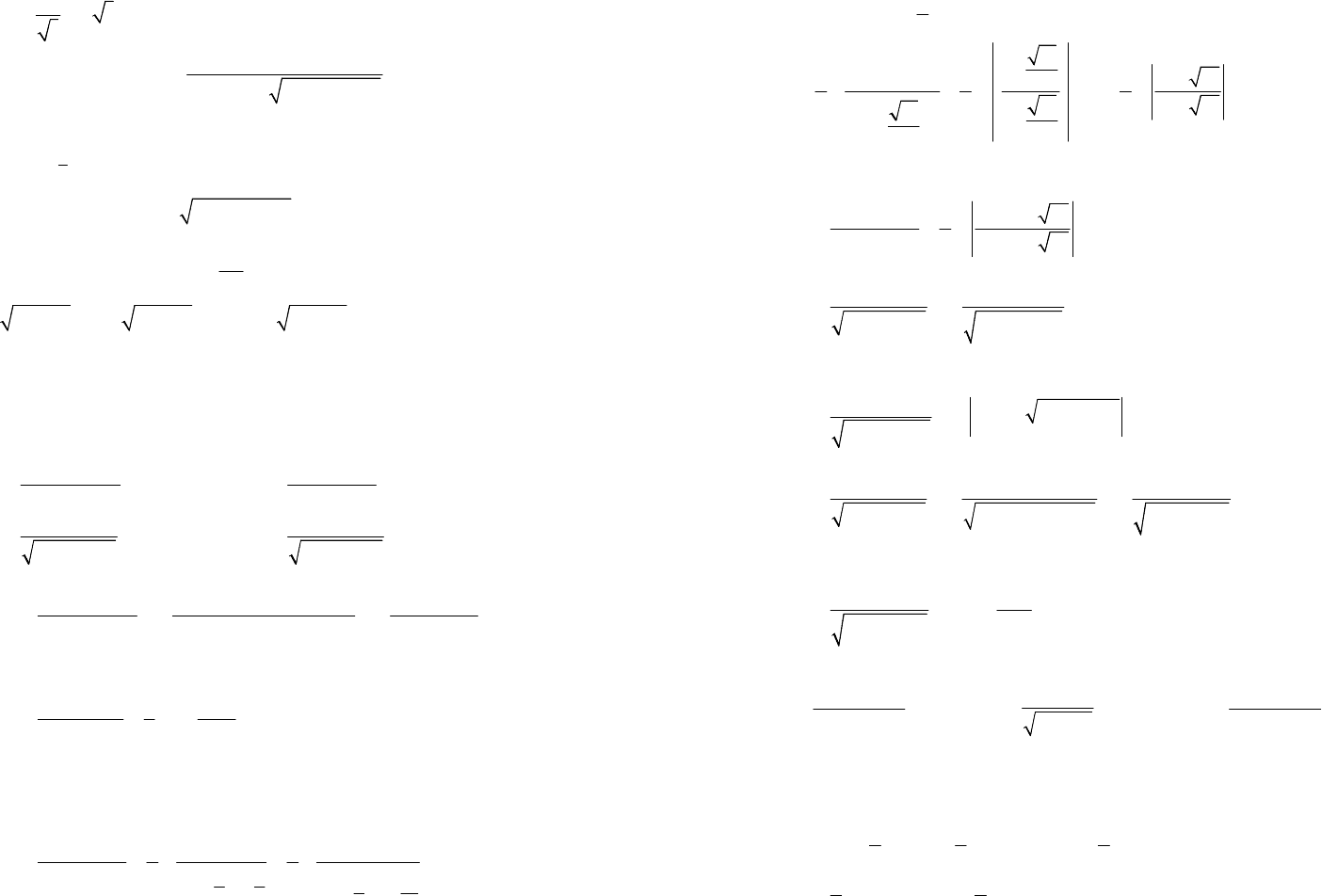
21
лов 2
dt
tC
t
=+
∫
и вида (19.18).
Интегралы вида
( )
2
(1,2)
n
dx
n
pxqaxbxc
=
+++
∫
сводятся к
рассмотренным выше интегралам с помощью подстановки
1
.
pxq
t
+=
Интеграл вида
2
axbxcdx
++
∫
после выделения полного
квадрата и замены
2
b
tx
a
=+ сводится к одному из интегралов
22
,
tkdt
+
∫
22
tkdt
−
∫
или
22
,
ktdt
−
∫
которые могут быть
вычислены методом интегрирования по частям (см. п. 19.4.) или
с помощью тригонометрических подстановок (см. п. 19.7.), или
как интеграл от дифференциального бинома (см. п. 19.8).
Пример 1. Найти неопределенный интеграл:
1)
2
;
1458
dx
xx
−+
∫
2)
2
;
231
dx
xx
+−
∫
3)
2
;
45
dx
xx
−−
∫
4)
2
.
82
dx
xx
−−
∫
Решение: 1) Выделим в знаменателе дроби полный квадрат:
( )
222
.
145827494958
79
dxdxdx
xxxx
x
==
−+−⋅+−+
−+
∫∫∫
Используем метод поднесения под знак дифференциала. Интеграл
примет вид:
2
(7)17
arctg.
33
(7)9
dxx
C
x
−−
=+
−+
∫
Для вычисления последнего интеграла использовали формулу
(19.13) таблицы интегралов.
2) Вынесем в знаменателе подынтегрального выражения множи-
тель 2 за скобки и выделим полный квадрат, получим:
22
2
31
317
22
416
11
.
22
231
dxdxdx
xx
xx
x
==
+−
+−
+−
∫∫∫
22
Заменим
3
4
xt
+=
и
.
dxdt
=
Интеграл примет вид:
2
2
17
4
17
17
4
4
111417
lnln.
222
417
t
dtt
CC
t
t
t
−
−
=+=+
+
+
−
∫
Для вычисления последнего интеграла использовали формулу
(19.15) таблицы интегралов. Возвращаясь к переменной x, имеем:
2
14317
ln.
2
2314317
dxx
C
xxx
+−
=+
+−++
∫
3) Выделив в подкоренном выражении полный квадрат, получаем:
( )
22
.
45
29
dxdx
xx
x
=
−−
−−
∫∫
Используя метод поднесения под знак дифференциала и формулу
(19.16) таблицы интегралов, имеем:
( )
2
2
(2)
ln245.
29
dx
xxxC
x
−
=−+−−+
−−
∫
4) Выделим в подкоренном выражении полный квадрат:
( )
( )
22
2
.
82
912
91
dxdxdx
xx
xx
x
==
−−
−++
−+
∫∫∫
Применив метод поднесения под знак дифференциала и формулу
(19.14) таблицы интегралов, получаем:
(
)
( )
2
1
1
arcsin.
3
91
dx
x
C
x
+
+
=+
−+
∫
Пример 2. Найти неопределенный интеграл:
1)
(
)
2
3
;
820
xdx
xx
−
−+
∫
2)
2
61
;
4
x
dx
xx
−
−
∫
3)
2
1
.
367
x
dx
xx
−
−+
∫
Решение: 1) Найдем производную квадратного трехчлена, запи-
санного в знаменателе дроби,
( )
2
82028.
xxx
′
−+=−
Выделим производную знаменателя в числителе дроби:
( ) ( )
( )
111
32328832883
222
xxxx
−=⋅−=−+−=−+−=
( ) ( )
11
2843281.
22
xx
=−+−=−+
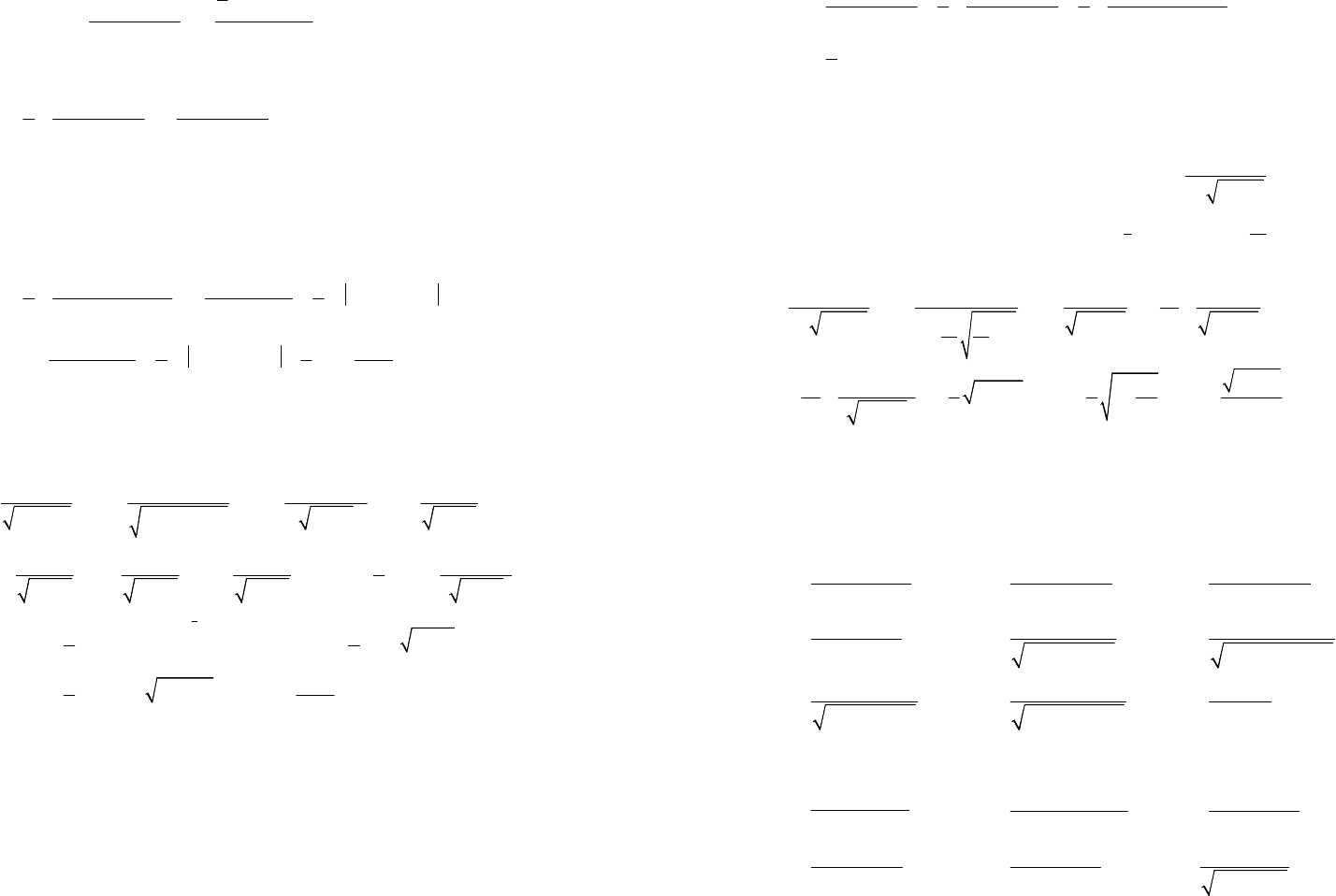
23
Тогда
( )
( )
22
1
2
281
3
.
820820
x
xdx
dx
xxxx
−+
−
=
−+−+
∫∫
Используя второе свойство неопределенного интеграла, предста-
вим данный интеграл в виде суммы двух интегралов
(
)
22
28
1
.
2
820820
xdx
dx
xxxx
−
+
−+−+
∫∫
Выделим в знаменателе второго интеграла полный квадрат:
( )
2
22
820816444.
xxxxx
−+=−++=−+
Для вычисления полученных интегралов используем метод подне-
сения под знак дифференциала и формулы (19.5) и (19.13) таблицы ин-
тегралов:
(
)
( )
2
2
22
18201
ln820
22
820
44
dxxdx
xx
xx
x
−+
+=−++
−+
−+
∫∫
2
2
(4)114
ln820arctg.
222
(4)4
dxx
xxC
x
−−
+=−+++
−+
∫
2) Выделим в подкоренном выражении полный квадрат:
(
)
( )
2
22
444424.
xxxxx
−=−−+−=−−+
Заменив
2,
xt
−=
2,
xt
=+
,
dxdt
= получим:
( )
(
)
2222
621
6161611
444
42
t
xxt
dxdxdtdt
xxtt
x
+−
−−+
====
−−−
−−
∫∫∫∫
(
)
2
2222
624
11311arcsin3
2
4444
tdtdttdttdt
tttt
−−
=+=−+=−+
−−−−
∫∫∫∫
()
1
2
222
2
11arcsin34(4)11arcsin64
22
2
11arcsin6411arcsin.
22
tt
tdtt
tx
CxxC
−
+=−−−+=−−+
−
++=−−++
∫
Для вычисления суммы интегралов использовали метод поднесе-
ния под знак дифференциала и формулы (19.3) и (19.14) таблицы инте-
гралов.
3) Найдем производную квадратного трехчлена
( )
2
36766.
xxx
′
−+=−
Выделим ее в числителе дроби, чтобы получить дифференциал
знаменателя:
24
(
)
2
222
(1)1(66)1367
66
367367367
xdxxdxdxx
xxxxxx
−−−+
===
−+−+−+
∫∫∫
( )
2
1
ln367.
6
xxC
=−++
Для вычисления интеграла использовали метод поднесения под
знак дифференциала и формулу (19.5) таблицы интегралов.
Пример 3. Найти неопределенный интеграл
22
.
9
dx
xx
+
∫
Решение: Применим подстановку
1
,
x
t
=
тогда
2
1
.
dxdt
t
=− Полу-
чаем:
22
2222
2
11
118
18
91919
9
tt
dxdttdttdt
xxtt
t
=−=−=−=
+++
⋅+
∫∫∫∫
()
22
2
2
2
1191199
191.
18999
19
dtx
tCCC
x
x
t
++
=−=−++=−++=−+
+
∫
Задания
I уровень
1.1. Найдите неопределенный интеграл:
1)
2
;
417
dx
xx−+
∫
2)
2
;
962
dx
xx
++
∫
3)
2
;
248
dx
xx−−
∫
4)
2
;
34
dx
xx
−−
∫
5)
2
;
23
dx
xx
+−
∫
6)
2
;
4415
dx
xx−−
∫
7)
2
;
54
dx
xx
+−
∫
8)
2
;
369
dx
xx
+−
∫
9)
2
.
2
dx
xx
−
∫
1.2. Найдите неопределенный интеграл:
1)
2
3
;
613
x
dx
xx
−
−+
∫
2)
2
81
;
41213
x
dx
xx
−
−+
∫
3)
2
213
;
89
x
dx
xx
+
+−
∫
4)
2
1
;
45
x
dx
xx
+
++
∫
5)
2
45
;
23
x
dx
xx
+
+−
∫
6)
2
2
;
44
x
dx
xx
+
+
∫
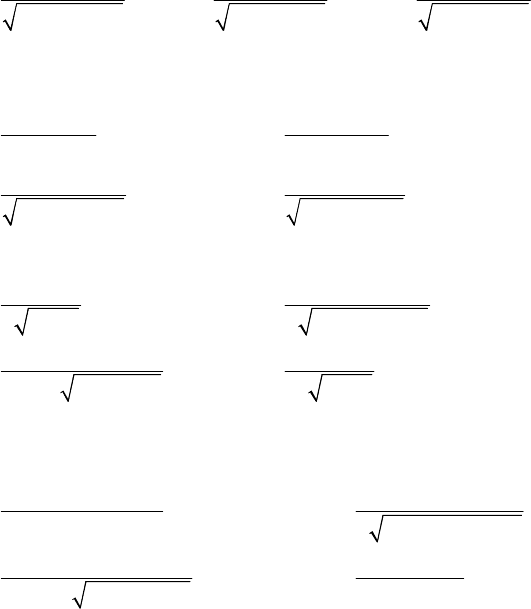
25
7)
2
63
;
412
x
dx
xx
+
+−
∫
8)
2
1
;
32
x
dx
xx
−
−−
∫
9)
2
41
.
54
x
dx
xx
+
−−
∫
II уровень
2.1. Найдите неопределенный интеграл:
1)
2
73
;
83
x
dx
xx
−
−+
∫
2)
2
65
;
321
x
dx
xx
−
−−
∫
3)
2
35
;
962
x
dx
xx
−
−−
∫
4)
2
23
.
134
x
dx
xx
+
−−
∫
2.2. Найдите неопределенный интеграл:
1)
2
;
1
dx
xx
+
∫
2)
2
;
2041
dx
xxx
−+
∫
3)
( )
2
;
182
dx
xtt
−−−
∫
4)
22
.
1
dx
xx
−
∫
III уровень
3.1. Найдите неопределенный интеграл:
1)
2
sin
;
cos4cos8
xdx
xx
−+
∫
2)
2
ln1
;
76lnln
x
dx
xxx
+
−−
∫
3)
( )
2
;
21541
dx
xxx
+++
∫
4)
42
.
25
xdx
xx
++
∫
19.4. Метод интегрирования по частям
Пусть функции
()
uux
=
и
()
x
νν
=
имеют непрерывные
производные
()
uux
′′
=
и
().
x
νν
′′
=
Тогда имеет место равенство
.
udvuvvdu
=−
∫∫
(19.20)
Формула (19.20) задает метод интегрирования по частям,
согласно которому интегрирование выражения udv сводится к
интегрированию выражения vdu Применение формулы (19.20)
предполагает, что в правой части интеграл
vdu
∫
может быть
26
вычислен легче, чем исходный. Формула (19.20) может быть за-
писана также в виде
.
uvdxuvvudx
′′
=−
∫∫
Рациональность вычисления некоторых интегралов зависит
от того, как выбраны функции
()
ux
и
()
vx
′
в заданном интеграле.
Формула интегрирования по частям может применяться не-
однократно.
Рассмотрим следующие случаи:
1. Для вычисления интегралов вида
(),
ax
n
Pxedx
∫
()sin,
n
Pxaxdx
∫
()cos,
n
Pxaxdx
∫
где
()
n
Px
– многочлен степени
n, в качестве функции
()
ux
следует взять многочлен
(),
n
Px
а в
качестве
dv
– одно из выражений
,
ax
edx
sin,
axdx
cos
axdx
соот-
ветственно. При этом формулу интегрирования по частям следу-
ет применять n раз.
2. Для интегралов вида cos
ax
ebxdx
∫
и sin
ax
ebxdx
∫
в каче-
стве функции
()
ux
можно взять
ax
e
или
cos
bx
(
)
sin.
bx
Форму-
лу интегрирования по частям следует применить дважды, а за-
тем из полученного равенства, как из уравнения, найти заданный
интеграл.
3. Для интегралов вида
()ln,
n
Pxxdx
∫
()arcsin,
n
Pxxdx
∫
()arccos,
n
Pxxdx
∫
()arctg,
n
Pxxdx
∫
()arcctg,
n
Pxxdx
∫
sinln,
xdx
∫
cosln
xdx
∫
в качестве u(x) берут функции lnx,
arcsin,
x
arccos,
x
arctg,
x
arcctg,
x
sinln,
x
cosln,
x
а в качестве dv – выражение
().
n
Pxdx
Такой подход используют и тогда, когда
()1.
n
Px
≡
Во многих случаях подынтегральная функция зависит не
только от аргумента, но и от натурального индекса n. Методом
интегрирования по частям удается привести интеграл к интегра-
лу такой же формы, но с меньшим значением индекса. После не-
скольких таких шагов приходят к интегралу, который можно
27
вычислить с помощью таблицы. Такой метод интегрирования
называют рекуррентным методом, а полученную формулу –
рекуррентной формулой.
Пример 1. Методом интегрирования по частям найти неопреде-
ленный интеграл:
1)
1
(51);
x
xedx
−
+
∫
2)
ln;
xdx
∫
3)
( )
2
23sin.
2
x
xxdx
−+
∫
Решение. 1) Положим
51,
ux
=+
1
.
x
dvedx
−
= Тогда
5,
dudx
=
1
.
x
ve
−
= Используя формулу (19.20) интегрирования по частям, полу-
чаем:
11111
(51)(51)5(51)5(1)
xxxxx
xedxxeedxxeedx
−−−−−
+=+−⋅=+−−=
∫∫∫
(
)
(
)
(
)
1111
51551554.
xxxx
xeeCxeCxeC
−−−−
=+−+=+−+=−+
2) Применим формулу (19.20) интегрирования по частям:
ln,,
lnln
,
uxdvdx
dx
xdxxxx
dx
duvx
x
x
==
==−=
==
∫∫
lnln.
xxdxxxxC
=−=−+
∫
3) Положим
2
23,
uxx
=−+
sin.
2
x
dvdx
= Тогда
2cos,
2
x
v =−
(
)
(
)
2221.
duxdxxdx
=−=− Применяя формулу (19.20), получаем:
( ) ( )
( )
22
23sin223cos2cos21
222
xxx
xxdxxxxdx
−+=−−+−−⋅−=
∫∫
()
()
2
223cos41cos.
22
xx
xxxdx
=−−++−
∫
Применив формулу интегрирования по частям, понизили степень
многочлена на единицу. Чтобы найти
( )
1cos,
2
x
xdx
−
∫
применим еще
раз метод интегрирования по частям. Положим
1,
ux
=−
cos.
2
x
dvdx
=
Тогда
,
dudx
=
2sin.
2
x
v = Получаем:
( )
( )
2
223cos421sin2sin
222
xxx
xxxdx
−−++−−=
∫
28
( )
( )
2
223cos81sin8sin
222
xxx
xxxdx
=−−++−−=
∫
( )
( )
2
223cos81sin16cos
222
xxx
xxxC
=−−++−++=
( )
( )
2
225cos81sin.
22
xx
xxxC
=−−−+−+
Пример 2. Методом интегрирования по частям найти неопреде-
ленный интеграл:
1)
2
4;
xdx
−
∫
2)
2
cos3.
x
exdx
∫
Решение. 1) Интеграл
2
4
xdx
−
∫
уже был вычислен в параграфе
19.2. (см. пример 2, с. 15–16 данного пособия) методом подстановки.
Рассмотрим второй способ его вычисления, используя метод интегри-
рования по частям:
( )
2
2
22
2
22
222
22
2
22
222
4
4,,
44
,
4
44
444
44
44
444.
444
xdx
x
uxdvdx
xdx
xdxxxx
duvx
x
xdxx
xxxxdxxx
xx
xdx
dxdxxxxdx
xxx
−
−
=−=
−
−==−−⋅=
==
−
−−−
=−−=−−=−−
−−
−
−+=−−−+
−−−
∫∫
∫∫
∫∫∫∫
Вычислим последний интеграл, используя формулу (19.14) табли-
цы интегралов. Получим равенство
222
4444arcsin.
2
x
xdxxxxdx−=−−−+
∫∫
В правой части этого равенства получили исходный интеграл.
Найдем его из уравнения:
22
2444arcsin,
2
x
xdxxx−=−+
∫
откуда
получаем ответ:
22
442arcsin.
22
xx
xdxxC
−=−++
∫
2) Используя формулу интегрирования по частям дважды, получаем:
2
2
2
1
3
,cos3,
cos3
2,sin3
x
x
x
uedvxdx
exdx
duedxvx
==
==
==
∫
29
2222
2
2
222
222
1
3
1112
sin3sin32sin3sin3
3333
,sin3,
2,cos3
1211
sin3cos3cos32
3333
124
sin3cos3cos3.
399
xxxx
x
x
xxx
xxx
exxedxexexdx
uedvxdx
duedxvx
exexxedx
exexexdx
=−⋅=−=
==
==
==−
=−−−−⋅=
=+−
∫∫
∫
∫
В результате получили равенство
2222
124
cos3sin3cos3cos3,
399
xxxx
exdxexexexdx
=+−
∫∫
из которого находим:
222
1312
cos3sin3cos3;
939
xxx
exdxexex
=+
∫
222
912
cos3sin3cos3.
1339
xxx
exdxexex
=+
∫
Приходим к ответу:
( )
2
2
cos33sin32cos3.
13
x
x
e
exdxxxC
=++
∫
Пример 3. Найти неопределенный интеграл
2
sincos.
xxxdx
∫
Решение. Используя формулу (19.20) интегрирования по частям,
получаем:
( )
( )
3
2
2
22
3332
3
323
3
sin
3
,sincos,
sincos
,sincossin(sin)
1111
sinsinsinsinsin
3333
1111cos
sin1coscossincos
33333
111
sincoscos
339
x
uxdvxxdx
xxxdx
dudxvxxdxxdx
xxxdxxxxxdx
x
xxxdxxxxC
xxx
==
==
====
=−=+−=
=+−=+−+=
=+−
∫
∫∫
∫∫
∫
3
.xC+
Пример 4. Найти неопределенный интеграл
( )
3
2
.
16
dx
x +
∫
30
Решение. Преобразуем подынтегральное выражение:
( ) ( )
(
)
( )
( ) ( )
22
333
222
2
23
22
116116
1616
161616
11
.
1616
1616
dxdxxx
dx
xxx
dxxdx
xx
+−
===
+++
=−
++
∫∫∫
∫∫
Последний интеграл вычислим, применяя формулу интегрирова-
ния по частям.
Полагаем
,
ux
=
.
dudx
=
Если
( )
(
)
( )
( ) ( )
2
3
22
33
22
1161
1616,
22
1616
xdxdx
dvxdx
xx
−
+
===++
++
то
( ) ( )
( )
( )
2
2
3
22
2
2
11161
1616.
222
416
x
vxdx
x
−
−
+
=++==−
−
+
∫
Тогда
2
232222
1
.
4
(16)4(16)(16)
xdxxdx
xxx
=−+
+++
∫∫
Таким образом, получаем выражение интеграла
( )
3
2
16
dx
x +
∫
через
интеграл
( )
2
2
.
16
dx
x +
∫
( ) ( ) ( ) ( )
3222
2222
111
16164
161641616
dxdxxdx
xxxx
=−−+=
++++
∫∫∫
()()()
()()
222
222
22
22
11
1664
16641616
3
.
64
166416
dxxdx
xxx
dxx
xx
=+−=
+++
=+
++
∫∫
∫
Вычисляем
( )
2
2
16
dx
x +
∫
аналогично первоначальному.
( ) ( )
(
)
( )
22
222
222
116116
1616
161616
dxdxxx
dx
xxx
+−
===
+++
∫∫∫
() ()
22
222
22
1111
arctg.
161664416
16
1616
dxxdxxxdx
x
xx
=−=−
+
++
∫∫∫
31
Для вычисления последнего интеграла применяем формулу интег-
рирования по частям:
( )
( )
( )
( )
( )
( )
( ) ( )
( )
( )
2
22
22
2
2
2
22
2
2
2
2
1
2
2
,,
116
,
2
1616
1161
1616
16
22
16
1161
.
21
216
uxdudx
xdxdx
dv
xx
xdx
dx
vxdx
x
x
x
x
−
−
==
+
==
++
+
==
==++=
+
+
+
==−
−
+
∫
∫∫
() ()
2
22
11
arctg.
284
16
216216
xdxxx
x
xx
=−+=−+
+
++
∫
Имеем:
( )
( )
( ) ( )
2
2
2
22
111
arctgarctg
6441684
216
16
111
arctgarctgarctg.
64412841284
32163216
dxxxx
x
x
xxxxx
xx
=−−+=
+
+
=+−=+
++
∫
Получаем:
( ) ( )
( )
( )
( )
32
2
22
2
2
2
31
arctg
641284
3216
166416
33
arctg.
81924
204816
6416
dxxxx
x
xx
xxx
C
x
x
=++=
+
++
=+++
+
+
∫
Пример 5. Получить рекуррентную формулу для вычисления ин-
теграла
cos,N,2.
n
xdxnn
∈≥
∫
Используя ее, вычислить
5
cos.
xdx
∫
Решение. Обозначим
cos.
n
n
Ixdx
=
∫
( )
( ) ( )
( )
( ) ( )
1
1
1
2
22122
12
coscoscos
cos,cos,
cossin
1cossin,sin
1cossincossin1cos1cos
cossin1cos1cos.
nn
n
n
n
n
nnn
nnn
Ixdxxxdx
uxdvxdx
xx
dunxxdxvx
nxxdxxxnxxdx
xxnxdxnxdx
−
−
−
−
−−−
−−
===
==
==+
=−−=
+−=+−−=
=+−−−
∫∫
∫∫
∫∫
32
Мы получили:
( ) ( )
12
cossin1cos1.
nn
nn
IxnxdxnI
−−
=+−−−
∫
Выражаем:
1
2
11
cossin.
n
nn
n
IxxI
nn
−
−
−
=+
Это и есть рекуррентная формула, которая позволяет уменьшать
показатель степени в подынтегральной функции до тех пор, пока не
придем к интегралу cossin
xdxxC
=+
∫
или
dxxC
=+
∫
в зависимо-
сти от того, является ли n числом четным или нечетным.
Используем ее для вычисления
5
5
cos.
Ixdx
=
∫
543
5
14
coscossincos
55
Ixdxxxxdx
==+=
∫∫
42
1412
cossincossincos
5533
xxxxxdx
=++=
∫
42
148
cossincossinsin.
51515
xxxxxC
=+++
Задания
I уровень
1.1. Найдите интеграл методом интегрирования по частям:
1)
( )
32;
x
xedx
+
∫
2)
( )
52sin3;
xxdx
−
∫
3)
( )
2
5cos;
3
x
xdx
+
∫
4)
( )
4sh2;
xxdx
+
∫
5)
( )
73ch;
3
x
xdx
+
∫
6)
.
x
x
dx
e
∫
1.2. Найдите интеграл методом интегрирования по частям:
1)
( )
2
5cos2;
xxxdx
−+
∫
2)
( )
( )
2
231sin32;
xxxdx
+−+
∫
3)
( )
2
2;
x
xxedx
+−
∫
4)
( )
231
31;
x
xxedx
−
++
∫
5)
( )
2
313;
x
xxdx
−−
∫
6)
( )
23
522.
x
xxdx
++
∫
33
1.3. Найдите интеграл методом интегрирования по частям:
1)
arctg;
xdx
∫
2)
ln;
xdx
∫
3)
2
;
sin
x
dx
x
∫
4)
2
;
cos
x
dx
x
∫
5)
arctg71;
xdx
−
∫
6)
( )
2
ln9.
xdx
+
∫
1.4. Найдите интеграл методом интегрирования по частям:
1)
5
sin2;
x
exdx
∫
2)
cos;
x
exdx
−
∫
3)
2
sin;
3
x
x
edx
−
∫
4)
5cos3;
x
xdx
∫
5)
sinln;
xdx
∫
6)
cosln;
xdx
∫
7)
sinln5;
xdx
∫
8)
22
cos;
x
exdx
∫
9)
2
4.
xdx
−
∫
II уровень
2.1. Найдите интеграл:
1)
arccos
;
1
x
dx
x−
∫
2)
arctg;
xdx
∫
3)
2
cos;
xxdx
∫
4)
arcsin
;
1
x
dx
x +
∫
5)
arcsin
;
1
x
dx
x−
∫
6)
2
sin;
xxdx
∫
7)
( )
arcsin65;
xdx
−
∫
8)
( )
arccos1;
xdx
−
∫
9)
( )
( )
22
323sin21;
xxxdx
−−−
∫
10)
( )
( )
322
24cos32.
xxxdx
−++
∫
2.2. Найдите интеграл:
1)
3
ln;
xxdx
∫
2)
3
ln
;
xdx
x
∫
3)
1
ln1;
xdx
x
+
∫
4)
2
ln
;
x
dx
x
∫
5)
2
ln;
xxdx
∫
6)
( ) ( )
2
2ln2;
xxdx
−−
∫
7)
( ) ( )
2
2
1ln1;
xxdx
++
∫
8)
( ) ( )
3
2
2ln2.
xxdx
++
∫
34
2.3. Найдите интеграл:
1)
3
arctg;
xxdx
∫
2)
2
arccos;
xxdx
∫
3)
arcsin;
xxdx
∫
4)
2
arcsin.
xdx
∫
2.4. Найдите интеграл:
1)
( )( )
25
13;
xxdx
+−
∫
2)
( )( )
23
2132;
xxdx
+−
∫
3)
( )
32
2123;
xxxxdx
−+−+
∫
4)
2
3
71
.
21
xx
dx
x
−+
+
∫
2.5. Найдите интеграл, комбинируя методы интегрирования
по частям и замены переменной:
1)
;
x
edx
∫
2)
cos;
xxdx
∫
3)
2
3
;
x
xedx
∫
4)
( )
ln1;
xx
eedx
+
∫
5)
(
)
2
lnarctg
;
1
xdx
x+
∫
6)
sinlncos;
xxdx
∫
7)
coslnsin;
xxdx
∫
8)
sin2lnsin.
xxdx
∫
III уровень
3.1. Найдите интеграл:
1)
2
1;
xdx
+
∫
2)
2
1;
xdx
−
∫
3)
2
4;
xdx
−
∫
4)
2
9;
xdx
+
∫
5)
2
25;
xdx
−
∫
6)
2
22.
xxdx
−+
∫
3.2. Получите рекуррентную формулу для вычисления инте-
грала и с ее помощью найдите интеграл для указанного n:
1)
( )
22
,2;
n
dx
n
xa
=
+
∫
2)
sin,4;
n
xdxn
=
∫
3)
ln,1,3;
n
xxdxn
α
α
≠−=
∫
4)
( )
22
,2;
n
axdxn
−=
∫
5)
22
,4;
n
xdx
n
xa
=
+
∫
6)
sincos,,;
mn
xxdxnm
∈
∫
N
35
7)
ln,3;
n
xdxn
=
∫
8)
,5;
nx
xedxn
=
∫
9)
sin,2;
xn
exdxn
α
=
∫
10)
,,4;
sin
n
dx
nn
x
∈=
∫
N
11)
tg,3;
n
xdxn
=
∫
12)
ctg,2;
n
xdxn
=
∫
13)
sin
,,,3,2.
cos
n
m
x
dxnmnm
x
∈==
∫
N
19.5. Рациональные функции. Интегрирование
простейших дробей
Рациональной функцией или рациональной дробью назы-
вается функция вида
()
,
()
n
m
Px
Qx
где
(),
n
Px
()
m
Qx
– многочлены с
рациональными коэффициентами степеней n и m соответствен-
но. Если
,
nm
<
то дробь называется правильной, если
,
nm
≥
то – неправильной.
Всякую неправильную дробь путем деления числителя на
знаменатель можно представить в виде суммы многочлена и
правильной дроби
()()
(),
()()
nk
nm
mm
PxRx
Sx
QxQx
−
=+
где
(),
nm
Sx
−
()
k
Rx
– многочлены,
()
()
k
m
Rx
Qx
– правильная
дробь,
.
km
<
Интегрирование рациональных дробей сводится к интегри-
рованию многочлена S(x) и правильной рациональной дроби
()
.
()
Rx
Qx
Если выражение в знаменателе правильной дроби разла-
гается на множители, то ее можно представить в виде суммы
простейших дробей (методы разложения на сумму простейших
дробей смотрите в параграфе 2.3, часть 1, с. 47–54).
Среди правильных дробей различают четыре типа простей-
36
ших дробей:
I
;
A
xa
−
II
( )
;
k
A
xa
−
III
2
;
MxN
xpxq
+
++
IV
( )
2
,2,
k
MxN
k
xpxq
+
≥
++
где A, M, N, a, p, q – постоянные действительные числа,
k – натуральное число, дискриминант
2
40.
Dpq
=−<
Неопределенные интегралы от простейших дробей
1.
()
ln.
Adxdxa
À AxaC
xaxa
−
==−+
−−
∫∫
2.
1
1
()(),
1
()()
k
kk
AdxA
AxadxaC
k
xaxa
−
−
=−−=+
−
−−
∫∫
,2.
kk
∈≥
N
3. Интегрирование простейшей дроби III типа производят
соответственно способу вычисления интеграла (19.19), который
описан в параграфе 19.3.
4. В числителе дроби IV типа выделим производную квад-
ратного трехчлена
2
:
xpxq
++
( ) ( )
22
22
(2)
.
kk
MMp
xpN
MxN
xpxqxpxq
++−
+
=
++++
Тогда
( ) ( )
( )
22
2
2
2
.
2
kk
k
MxNMxp
dxdx
xpxqxpxq
Mpdx
N
xpxq
++
=+
++++
+−
++
∫∫
∫
Вычислим интегралы последней суммы отдельно.
Согласно формуле (19.3) таблицы интегралов, имеем:
37
( )
(
)
( )
2
22
2
22
kk
dxpxq
MxpM
dx
xpxqxpxq
++
+
==
++++
∫∫
()()
()
1
2
22
221
k
k
xpxq
MM
xpxqdxpxqC
k
−+
−
++
=++++=⋅+=
−+
∫
( )
1
2
.
2(1)
k
M
C
kxpxq
−
=+
−++
Для вычисления второго интеграла выделим в знаменателе
полный квадрат:
( )
2
2
2
.
24
k
k
pp
xpxqxq
++=++−
Сделаем замену пе-
ременной
.
2
p
tx=+ Обозначив
2
2
0,
4
p
aq
=−>
получим:
( )
2
2
2
2
24
22
kk
p
pp
dx
MpdxMp
NN
xpxq
xq
+
−=−=
++
++−
∫∫
()
22
.
2
k
Mpdt
N
ta
=−
+
∫
Последний интеграл, который обозначим
,
k
I
вычисляется
по рекуррентной формуле
1
2212222
121
,,
()2()2
kk
kk
dxxk
IIk
xakaxaka
+
+
−
==+∈
++
∫
N
(19.21)
где
1
22
1
arctg.
dxx
IC
aa
xa
==+
+
∫
В частности,
2
2222223
1
arctg.
()2()2
dxxx
IC
a
xaaxaa
==++
++
∫
Интегралы вида
21
2
,
()
m
n
x
dx
abx
+
+
∫
где m – целое положитель-
ное число, вычисляются с помощью замены
2
.
abxt
+=
Тогда
38
2
,
ta
x
b
−
=
2,
dtbxdx
=
( )
( )
2122
111
2.
22
2
m
m
m
mm
m
ta
xdxxxdxxxdxdttadt
b
b
+
−
====−
Эта замена приводит к интегралу
( )
1
1
.
2
m
mn
ta
dt
bt
+
−
∫
Пример 1. Найти интегралы:
1)
2
32
64
;
2
xx
dx
xxx
−−
+−
∫
2)
432
32
61034
;
54
xxxx
dx
xxx
++−+
++
∫
3)
( )( )
2
2
8
;
31
xx
dx
xx
+−
−+
∫
4)
2
3
31
.
(1)
xx
dx
xx
−−
−
∫
Решение. 1) Разложим на множители знаменатель дроби:
(
)
( )( )
322
2212.
xxxxxxxxx+−=+−=−+
Так как каждый множитель
,1
xx
−
и
2
x
+
входит в знаменатель
в первой степени, то каждому из них соответствует простейшая дробь I
типа. Тогда общий вид разложения на сумму простейших дробей будет
иметь вид:
( )( )
2
64
.
1212
xxABC
xxxxxx
−−
=++
−+−+
Приведем правую часть к общему знаменателю:
( )( )
(
)
(
)
(
)
(
)
2
1221
64
.
12(1)(2)
AxxBxxCxx
xx
xxxxxx
−++++−
−−
=
−+−+
Приравнивая числители, получаем:
( )( ) ( ) ( )
(
)
22
6412212
xxAxxBxxCxxAxx
−−=−++++−=+−+
(
)
(
)
( ) ( )
22222
2
222
22.
BxxCxxAxAxABxBxCxCx
ABCxABCxA
+++−=+−+++−=
=++++−−
Два многочлена равны, если равны коэффициенты при одинако-
вых степенях переменной x. Приравняем эти коэффициенты:
2
1
0
1,
26,
24.
x
ABC
xABC
A
x
++=
+−=−
−=−
Получили систему уравнений
