Майсеня Л.И. Математика в примерах и задачах. Часть 4
Подождите немного. Документ загружается.

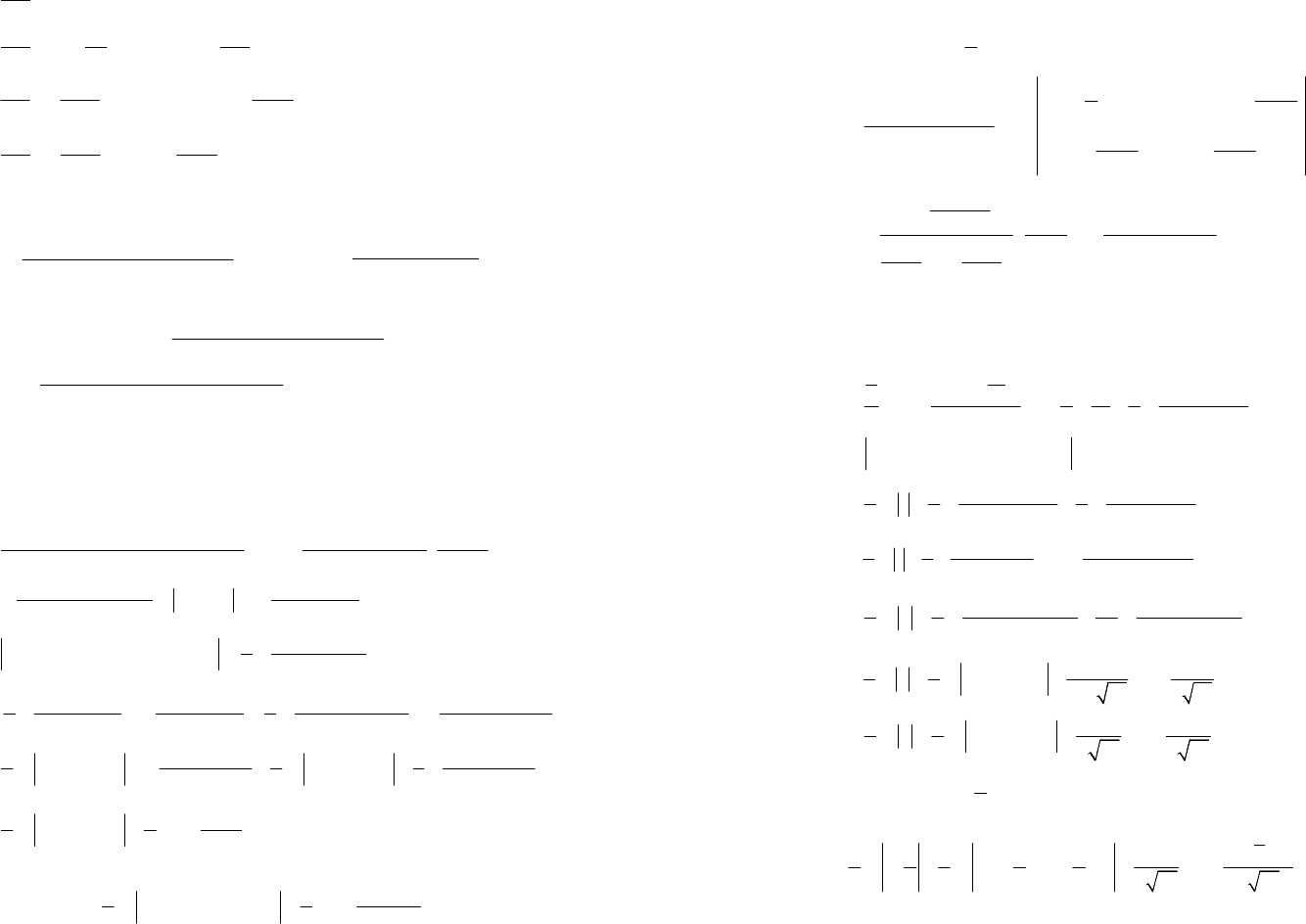
59
( )
1
32cos20cos40
128
311
cos20cos40
12864128
xxdx
dxxdxxdx
=−+=
=−+=
∫
∫∫∫
( ) ( )
311
cos2020cos4040
12812805120
xxdxxdx
=−+=
∫∫
311
sin20sin40.
12812805120
xxxC
=−++
Пример 6. Найти неопределенный интеграл:
1)
22
3tg2
;
5cos3sin29sin
x
dx
xxx
+
++
∫
2)
45cos
.
sin(73sin)
x
dx
xx
+
+
∫
Решение. 1) Запишем подынтегральную функцию
( )
22
22
3tg2
sin,cos
5cos3sin29sin
3tg2
.
5cos6sincos9sin
x
Rxx
xxx
x
xxxx
+
==
++
+
=
++
Так как подынтегральная функция является четной по sin x и cos x,
т. е.
(sin,cos)(sin,cos),
RxxRxx
−−= то применим подстановку
tg.
tx
=
Вначале умножим и поделим знаменатель подынтегрального
выражения на
2
cos,
x
получаем:
( )
2222
22
2
2
3tg 23tg2
5cos6sincos9sin569cos
(3tg2)(tg)(32)
tg
56tg9tg965
1866
1
(965)(186)
6
965
xxdx
dx
xxxxtgxtgxx
xdxtdt
tx
xxtt
t
dtttdtdt
tt
++
=⋅=
++++
++
=====
++++
++
=++=+==
++
∫∫
∫∫
∫
2
2222
1(186)1(965)
66
9659659659614
tdtdtdttdt
tttttttt
+++
=+=+=
+++++++++
∫∫∫∫
22
22
111(31)
ln965ln965
663
(31)4(31)4
dtdt
tttt
tt
+
=+++=+++=
++++
∫∫
2
1131
ln965arctg.
662
t
ttC
+
=++++
Возвращаемся к заданной переменной, заменяем t на tg x и прихо-
дим к ответу:
2
113tg1
ln9tg6tg5arctg.
662
x
xxC
+
++++
60
2) Поскольку подынтегральная функция не является нечетной ни
по sin x, ни по cos x, то применим универсальную тригонометрическую
подстановку
tg
2
x
t = и формулы (19.30). Получаем:
( )
2
2
22
2
tg,2arctg,,
45cos
2
1
21
sin73sin
sin,cos.
11
xdt
txtdx
x
t
dx
tt
xx
xx
tt
===
+
+
==
−
+
==
++
∫
( )
2
2
2
2
2
22
5(1)
1
26
11
4
29
.
1
767
7
t
t
tt
tt
dtt
dt
t
ttt
−
+
++
+
−
==
+
++
+
∫∫
Разложив подынтегральную функцию на сумму простейших дро-
бей, сводим заданный интеграл к разности двух интегралов, которые
вычисляем:
22
54
7
9
7
10
917054
77
767767
t
dtt
dtdtdt
tt
tttt
+
+
−=−=
++++
∫∫∫∫
2
(767)(146)
dtttdt
=++=+=
(
)
22
7030
91124
ln
777
767767
tdt
dt
t
tttt
+
=−−=
++++
∫∫
22
95(146)
ln24
77
767494249
tdtdt
t
tttt
+
=−−=
++++
∫∫
2
22
95(767)24(73)
ln
777
767(73)40
dttdt
t
ttt
+++
=−−=
++++
∫∫
2
952473
lnln767arctg
77
7210210
t
tttC
+
=−++−+=
⋅
2
951273
lnln767arctg.
77
710210
t
tttC
+
=−++−+
Заменяя t на
tg,
2
x
приходим к ответу:
2
2
7tg3
9512
lntgln7tg67arctg.
72722
710210
x
xxx
tgC
+
−++−+
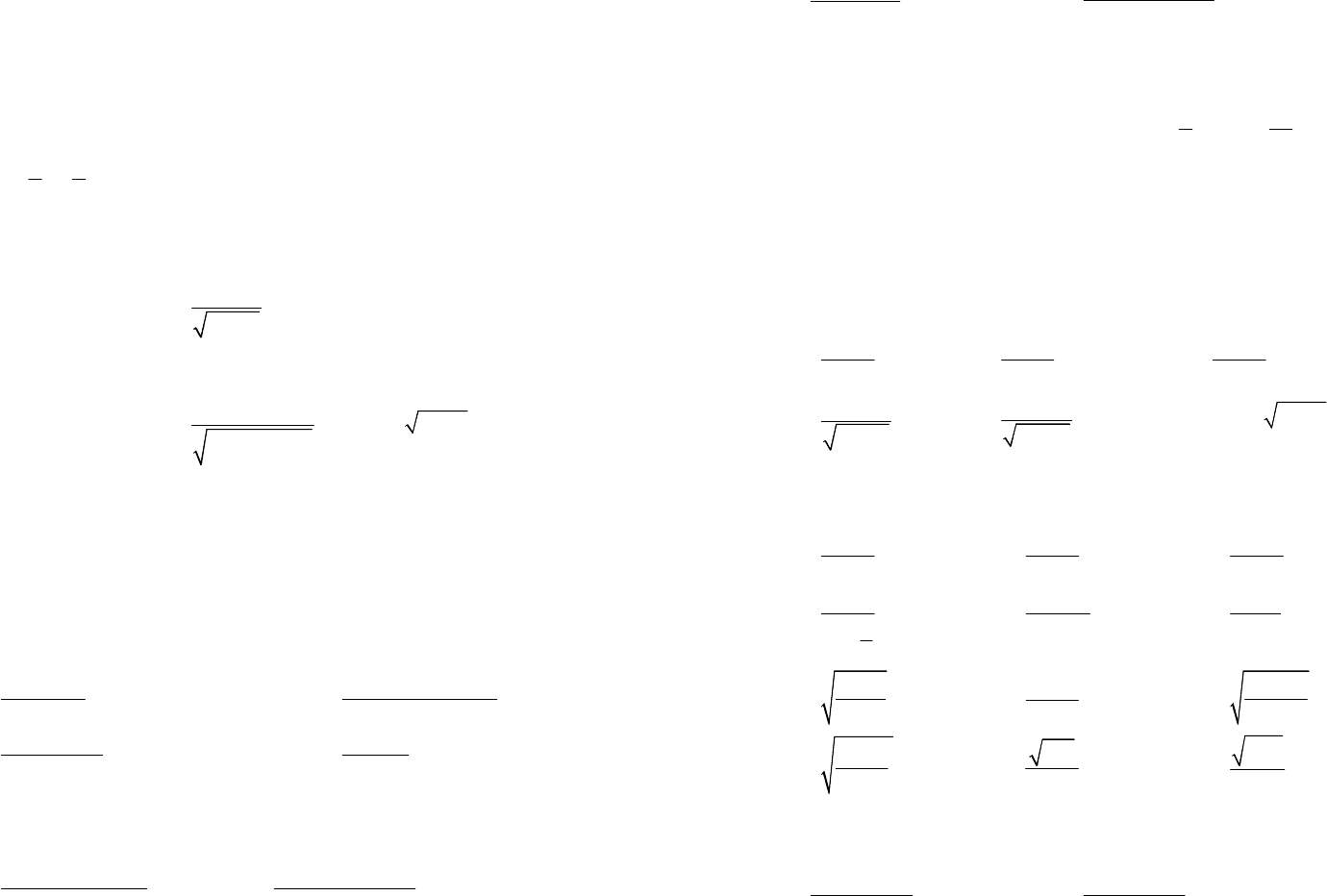
61
Задания
I уровень
1.1. Найдите неопределенный интеграл, преобразовав про-
изведение тригонометрических функций в сумму:
1)
sin3cos3;
xxdx
∫
2)
sin3cos5;
xxdx
∫
3)
sinsin;
32
xx
dx
∫
4)
cos4cos6.
xxdx
∫
1.2. Найдите неопределенный интеграл, применяя подста-
новку
sin
tx
=
или
cos:
tx
=
1)
5
sincos;
xxdx
∫
2)
3
2
sin
;
cos
x
dx
x
∫
3)
ctg;
xdx
∫
4)
tg;
xdx
∫
5)
3
sin;
xdx
∫
6)
3
cos;
xdx
∫
7)
7
cos3sin3;
xxdx
∫
8)
( )
7
cos2
;
sin23
x
dx
x −
∫
9)
5
sin3cos3.
xxdx
∫
1.3. Найдите неопределенный интеграл, используя формулы
понижения степени:
1)
2
cos;
xdx
∫
2)
2
sin2;
xdx
∫
3)
4
cos.
xdx
∫
1.4. Найдите неопределенный интеграл, используя универ-
сальную тригонометрическую подстановку:
1)
;
53cos
dx
x
−
∫
2)
;
54sin3cos
dx
xx
−+
∫
3)
;
sincos
dx
xx
+
∫
4)
.
1sin
dx
x
−
∫
1.5. Найдите неопределенный интеграл, используя подста-
новку
tg:
tx
=
1)
22
;
4sin9cos
dx
xx
+
∫
2)
22
;
16sincos
dx
xx
−
∫
62
3)
2
;
12sin
dx
x
+
∫
4)
2
tg3
.
tg6tg7
x
dx
xx
+
++
∫
II уровень
2.1. Найдите неопределенный интеграл:
1)
sin3cos4sin7;
xxxdx
∫
2)
3
sincoscos.
22
xx
xdx
∫
2.2. Найдите неопределенный интеграл, применяя подста-
новку
sin
tx
=
или
cos.
tx
=
1)
5
cos;
xdx
∫
2)
5
sin2;
xdx
∫
3)
7
sin;
xdx
∫
4)
43
cossin;
xxdx
∫
5)
25
sincos;
xxdx
∫
6)
32
sin2cos2;
xxdx
∫
7)
5
4
sin
;
cos
x
dx
x
∫
8)
3
2
cos
;
sin
x
dx
x
∫
9)
9
cos
;
sin
x
dx
x
∫
10)
3
7
4
sin
;
cos
x
dx
x
∫
11)
5
sin2
;
cos2
x
dx
x
∫
12)
5
73
cossin.
xxdx
∫
2.3. Найдите неопределенный интеграл, применяя подста-
новку
tg
tx
=
или
ctg:
tx
=
1)
4
8
cos
;
sin
x
dx
x
∫
2)
4
6
cos
;
sin
x
dx
x
∫
3)
3
7
sin
;
cos
x
dx
x
∫
4)
4
2
;
sin
x
dx
∫
5)
4
;
cos2
dx
x
∫
6)
6
;
sin
dx
x
∫
7)
5
cos
;
sin
x
dx
x
∫
8)
3
9
cos
;
sin
x
dx
x
∫
9)
3
7
sin3
;
cos3
x
dx
x
∫
10)
2
3
8
sin
;
cos
x
dx
x
∫
11)
3
6
tg
;
cos
x
dx
x
∫
12)
3
4
tg
.
cos
x
dx
x
∫
2.4. Найдите неопределенный интеграл, применяя подста-
новку
tg
tx
=
или
ctg:
tx
=
1)
55
;
sincos
dx
xx
∫
2)
33
;
sincos
dx
xx
∫
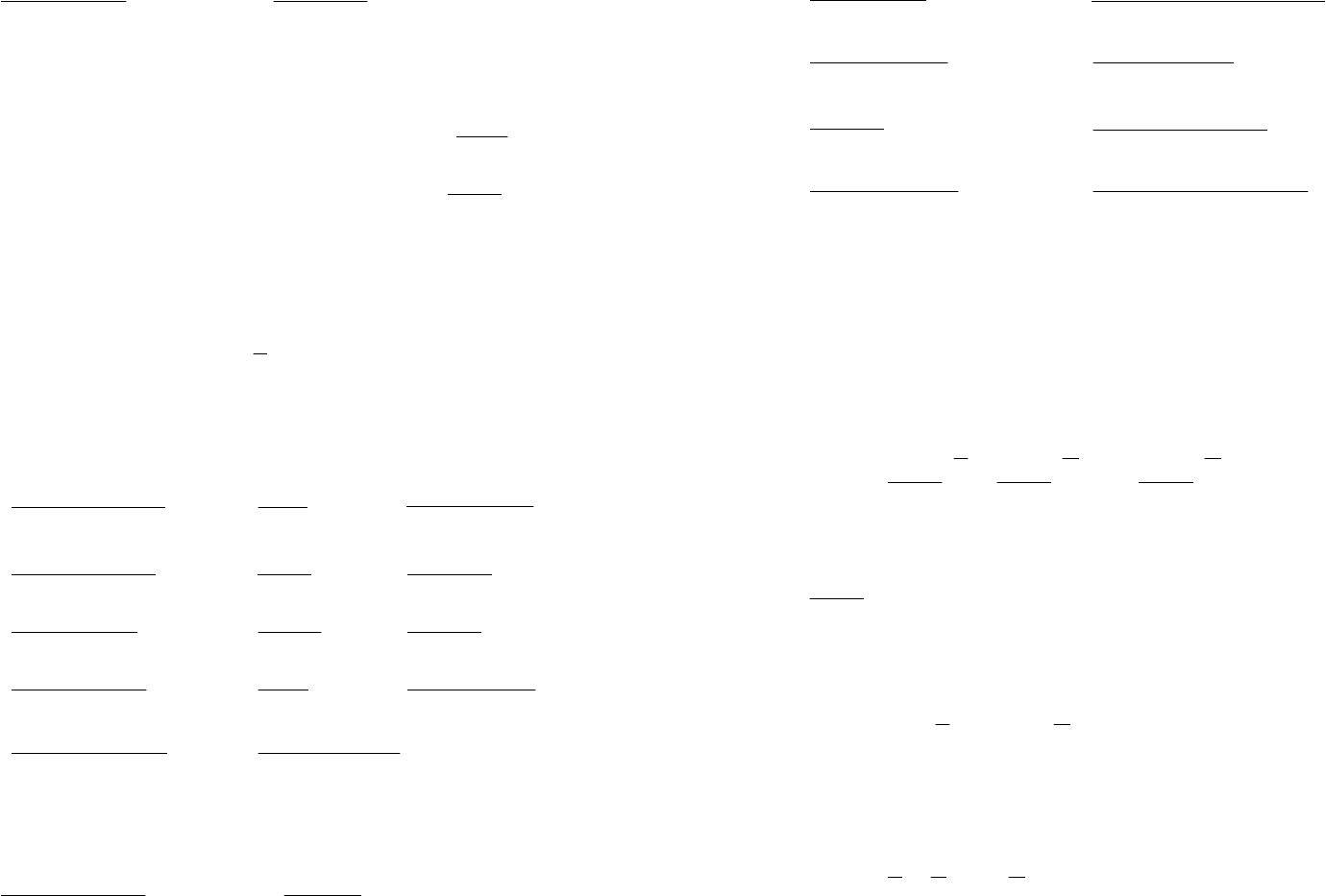
63
3)
46
;
sin2cos2
dx
xx
∫
4)
9
.
sincos
dx
xx
∫
2.5. Найдите неопределенный интеграл, применяя подста-
новку
tg
tx
=
или
ctg:
tx
=
1)
2
tg;
xdx
∫
2)
3
tg2;
xdx
∫
3)
4
tg;
xdx
∫
4)
6
4
1
ctg;
sin
xdx
x
∫
5)
6
tg;
xdx
∫
6)
5
tg3;
xdx
∫
7)
7
tg;
xdx
∫
8)
5
4
1
tg.
cos
xdx
x
∫
2.6. Найдите неопределенный интеграл:
1)
48
2cos;
xdx
∫
2)
6
sin;
xdx
∫
3)
66
sincos;
xxdx
∫
4)
24
sincos;
xxdx
∫
5)
4
cos;
2
x
dx
∫
6)
844
2sincos.
xxdx
∫
III уровень
3.1. Найдите неопределенный интеграл, используя универ-
сальную тригонометрическую подстановку:
1)
( )
2
sin
;
1cossin
xdx
xx
+−
∫
2)
3
;
sin
dx
x
∫
3)
;
2sincos
dx
xx
++
∫
4)
;
2sincos5
dx
xx
−+
∫
5)
7
;
cos
dx
x
∫
6)
cos
;
35cos
x
dx
x
+
∫
7)
3sin2cos
;
1cos
xx
dx
x
−
+
∫
8)
3
;
cos2
dx
x
∫
9)
2sin
;
2cos
x
dx
x
−
+
∫
10)
( )
;
cos1sin
dx
xx
−
∫
11)
7
;
sin
dx
x
∫
12)
cos
;
1cossin
xdx
xx
++
∫
13)
4sin5cos5
;
cos1
xx
dx
x
−−
+
∫
14)
( )
59sin
.
cos23sin
x
dx
xx
+
+
∫
3.2. Найдите неопределенный интеграл, используя подста-
новку
tg:
tx
=
1)
22
;
3cos5sin
dx
xx
+
∫
2)
2
;
1sin
dx
x
+
∫
64
3)
2
2tg2
;
tgtg1
x
dx
xx
+
++
∫
4)
22
42
;
7cos2sincossin
tgx
dx
xxxx
−
−+
∫
5)
( )
;
4tg1sin2
dx
xx
−
∫
6)
( )
2
32tg
;
sin2cos
x
dx
xx
+
+
∫
7)
47tg
;
tg2
x
dx
x
−
−
∫
8)
2
5tg2
;
3sin2sin22
x
dx
xx
+
++
∫
9)
2
2tg1
;
cossin21
x
dx
xx
−
−+
∫
10)
2
7tg1
.
3sinsin24cos2
x
dx
xxx
−
−−
∫
19.7. Интегрирование иррациональных функций
Основной метод вычисления интеграла от иррациональной
функции – метод рационализации (т. е. сведение к рациональной
функции), для чего делают определенную подстановку.
Алгебраическая подстановка
Интеграл вида
12
12
,,,...,,
n
n
ppp
qqq
axbaxbaxb
Rxdx
cxdcxdcxd
+++
+++
∫
(19.31)
где
1212
,,...,,,,...,
nn
pppqqq
– целые ненулевые числа, с
помощью подстановки
,
m
axb
t
cxd
+
=
+
(
)
12
,,...,,
n
m ÍÎÊ qqq
=
приводится к интегралу от рациональной функции.
Частные случаи интеграла (19.31):
1. Если
0,
c
=
1,
d
=
то интеграл имеет вид:
1
1
,(),...(),
n
n
p
p
qq
Rxaxbaxbdx
++
∫
и преобразуется в интеграл от рациональной функции с помо-
щью подстановки
(),
m
axbt
+= где
12
(,,...,).
n
m
НОК qqq
=
2. Если
0
=
=
cb
,
1
=
=
da
, то интеграл (19.31) имеет вид:
12
12
,,,...,,
n
n
p
pp
qqq
Rxxxxdx
∫
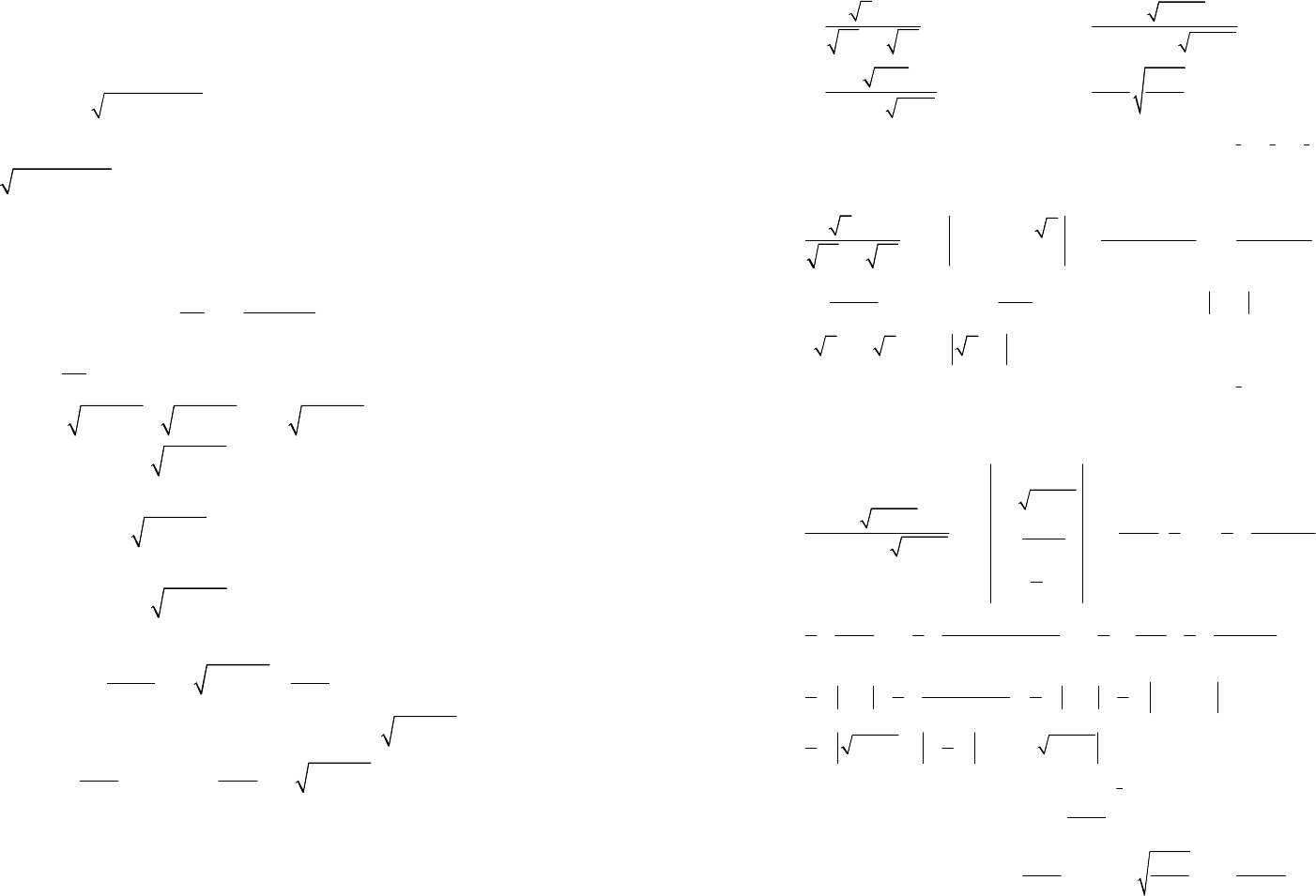
65
и сводится к интегралу от рациональной функции с помощью
подстановки
,
m
xt
= где
12
(,,...,).
n
m
НОК qqq
=
Тригонометрическая подстановка
Интегралы вида
2
(,),
Rxaxbxcdx
++
∫
где R – некоторая рациональная функция относительно x и
2
,
axbxc
++
могут быть вычислены с помощью тригонометри-
ческих подстановок, которые приводят его к интегралу от ра-
циональной функции.
В квадратном трехчлене выделим полный квадрат
2
2
2
2
4
2
4
bbac
axbxcax
a
a
−
++=+−
и применим подстановку
.
2
b
yx
a
=+ В результате под корнем получим одно из 3-х выра-
жений:
22
,
ky
−
22
ky
+ или
22
.
yk
−
Если имеем
22
,
ky
− то для уничтожения иррационально-
сти применим подстановку
sin,
ykt
=
в результате которой
cos,
dyktdt
=
22
cos.
kykt
−= Аналогично можно использо-
вать подстановку
cos.
ykt
=
Если имеем
22
,
ky
+ то для уничтожения иррационально-
сти применяется подстановка
tg,
ykt
=
в результате которой
имеем:
2
,
cos
k
dydt
t
=
22
.
cos
k
ky
t
+=
Если под интегралом есть выражение
22
,
yk
− то подстав-
ляем
,
cos
k
y
t
= т. е.
tg
,
cos
kt
dydt
t
=
22
tg.
ykkt
−=
Далее интеграл вычисляют как интеграл от тригонометриче-
ской функции и возвращаются к старой переменной, выражая
последовательно t через y и x.
66
Пример 1. Найти неопределенный интеграл:
1)
6
63
52
3
;
2
x
dx
xx
−
+
∫
2)
( )
2
132
;
3232
x
dx
xx
++
+−+
∫
3)
( )
2
61
;
12
x
dx
xx
+
++
∫
4)
22
.
22
xx
dx
xx
++
−−
∫
Решение. 1) Поскольку интеграл имеет вид:
(
)
152
663
,,,
Rxxxdx
а
(
)
3;66,
НОК
=
то применим подстановку
6
.
xt
=
Тогда
55
6
6
6
5
544
63
52
3(3)6(3)
,,
6
6
2(2)
2
xttdtttdt
xttx
dx
dxtdt
tttt
xx
−−−
==
====
=
++
+
∫∫∫
2
2
310
66533060ln2
22
tt
dttdttttC
tt
−
==−+=−+++=
++
∫∫
366
33060ln2.
xxxC
=−+++
2) Интеграл имеет вид:
( ) ( )
1
2
2
32,32,
Rxxdx
++
∫
поэтому
применим подстановку
2
32.
tx
=+
Тогда имеем:
2
2
243
32,
32,
132122(1)
2
,
33
(32)32(1)
3
2
3
tx
tx
xtttdt
t
dxtdt
x
xxtttt
dxtdt
=+
=+
++++
−
==⋅==
=
+−+−−
=
∫∫∫
322
21214221
33919
1(1)(1)1
ttdtt
dtdtdt
t
tttttt
+++
===−=
−
−−++++
∫∫∫∫
2
2
2
42(1)42
ln1ln1ln1
9999
1
dtt
ttttC
tt
++
=−−=−−+++=
++
∫
42
ln321ln3332.
99
xxxC
=+−−++++
3) Интеграл имеет вид:
1
2
1
,.
2
x
Rxdx
x
+
+
Применим подстановку
2
1
,
2
x
t
x
+
=
+
1
,
2
x
t
x
+
=
+
2
2
12
,
1
t
x
t
−
=
−
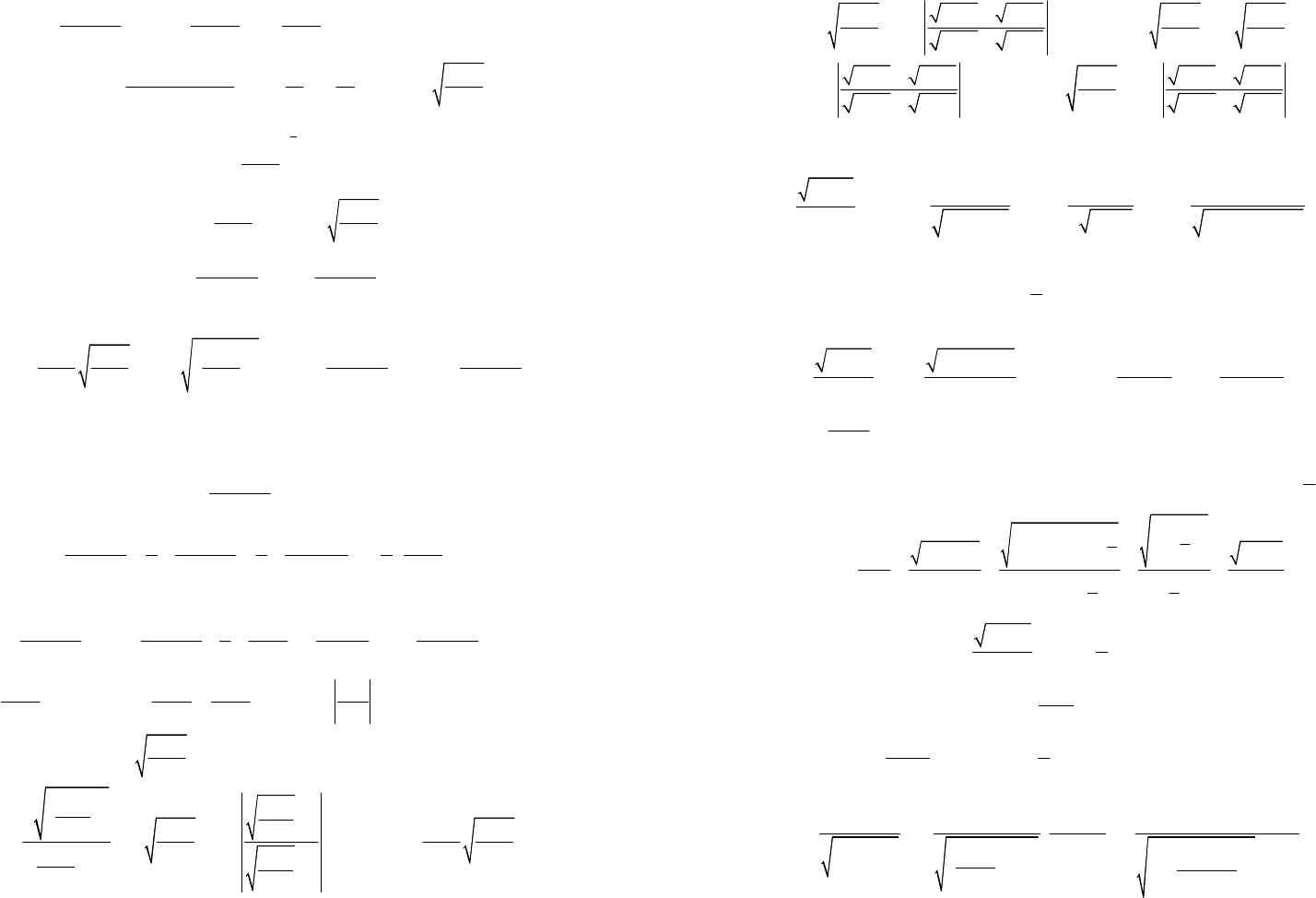
67
22
2
,
(1)
tdt
dx
t
=
−
22
22
12
11.
11
tt
x
tt
−−
+=+=
−−
Получаем:
222
4222
12(1)
122
1212.
1
(1)
ttdt
dtx
CC
tx
ttt
−
+
==−+=−+
+
−
∫∫
4) Интеграл имеет вид:
3
2
2
.
2
x
Rdx
x
+
−
Применим подстановку
2
2
,
2
x
t
x
+
=
−
2
,
2
x
t
x
+
=
−
(
)
2
22,
xtx+=−
22
(1)22,
xtt
−=+
2
2
2(1)
,
1
t
x
t
+
=
−
22
8
.
(1)
tdt
dx
t
−
=
−
Получаем интеграл
3
4
3
2222
2228
8.
222
(1)(1)
xxxtt
dxdxtdtdt
xxx
tt
+++−
===−
−−−
−−
∫∫∫∫
Для вычисления последнего интеграла вместо разложения на
простейшие дроби применим формулу интегрирования по частям.
Положим:
3
,
ut
=
2
3,
dutdt
=
22
,
(1)
tdt
dv
t
=
−
2
2222222
(1)
12111
.
222
(1)(1)(1)1
dt
tdttdt
v
tttt
−
====−
−−−−
∫∫∫
Получаем:
43232
222222
3411
8812
2
(1)2(1)1(1)1
tdtttdttt
dt
ttttt
−−+
−=−+=−=
−−−−−
∫∫∫
33
222
441
1212126ln.
1
111
tdttt
dttC
t
ttt
−
=−−=−−+
+
−−−
∫∫
Заменяем t на
2
,
2
x
x
+
−
тогда имеем:
( )
3
2
2
2
2
2
2
4
1
222
126ln2
2
222
1
1
2
x
x
x
x
x
x
xxx
Cx
x
xxx
x
+
+
−
−
+
−
−
+++
−−+=−−
+
−−−
−
+
−
68
( )
22222
126ln212
222
22
xxxxx
Cx
xxx
xx
++−−++
−−+=+−−
−−−
++−
22222
6ln(10)6ln.
2
2222
xxxxx
CxC
x
xxxx
+−−++−−
−+=−−+
−
++−++−
Пример 2. Найти неопределенный интеграл:
1)
2
2
9
;
x
dx
x
−
∫
2)
23
;
(4)
dx
x −
∫
3)
2
;
1
dx
xx
+
∫
4)
25
.
(25)
dx
xx++
∫
Решение. 1) Положим
3sin.
xt
=
Тогда
3cos,
dxtdt
=
arcsin.
3
x
t =
Интеграл примет вид:
2222
2222
999sin9cos1sin
3cos
9sin9sinsin
xttt
dxtdtdtdt
xttt
−−−
=⋅===
∫∫∫∫
2
ctg.
sin
dt
dtttC
t
=−=−−+
∫∫
Возвращаемся к заданной переменной, заменяем t на
arcsin.
3
x
Тогда
2
2
22
3
3
33
1
1sinarcsin
cos1sin9
ctg.
sinsin
sinarcsin
x
x
xx
ttx
t
ttx
−
−
−−
=====
Приходим к ответу:
2
9
arcsin.
3
xx
C
x
−
−−+
2) Применим подстановку
2
.
cos
x
t
=
Тогда
2
2sin
,
cos
t
dxdt
t
=
2
arccos.
t
x
=
Получаем интеграл
( )
2
333
2
2
32
2
2
4
1cos
cos
cos
12sin2sin
cos
4
4
4cos
t
t
t
dxtdttdt
t
x
t
−
=⋅==
−
−
∫∫∫
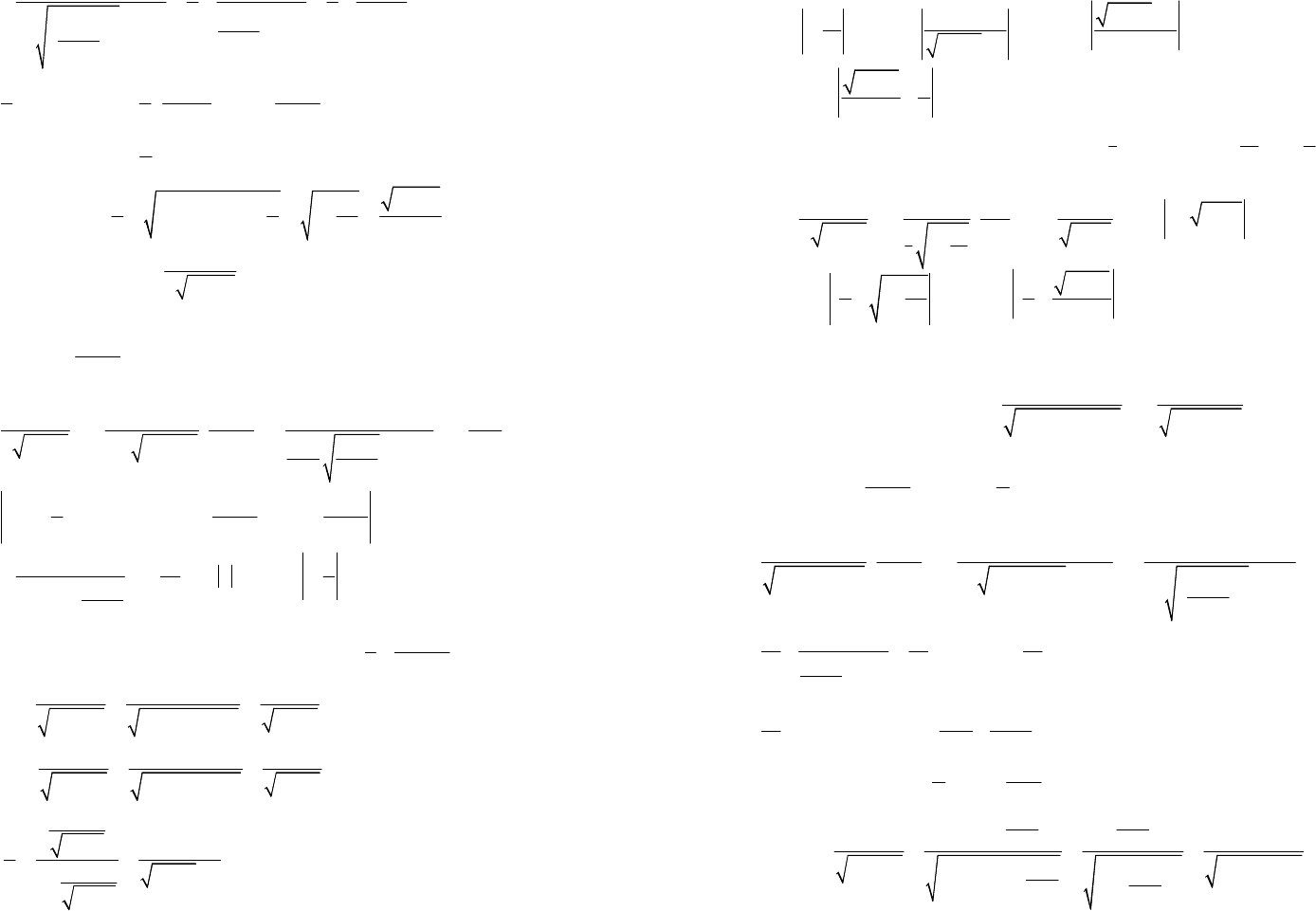
69
32
3
2
2
32
3
2
sin
sin
cos
cos
2sin1sin1cos
44
sin
cos
2cos
t
t
t
t
tdttdttdt
t
t
t
====
∫∫∫
1
2
11sin1
sinsin.
4414sin
t
tdtCC
t
−
−
==+=−+
−
∫
Заменяя t на
2
arccos,
x
получаем:
2
2
2
2244
sinsinarccos1cosarccos1.
x
t
xxx
x
−
==−=−=
Приходим к ответу:
2
.
44
x
C
x
−+
−
3) 1-й способ. Применим подстановку
tg.
xt
=
Тогда
2
,
cos
dt
dx
t
=
arctg.
tx
=
Интеграл примет вид:
2
22
2
2
sin1
cos
cos
1
sin
cos
1tg1tg
cos
t
t
t
dxdtdtdt
t
t
xxtt
t
=⋅===
++
⋅
∫∫∫∫
2
2
22
tg,2arctg,,sin
2
1
1
tdzz
ztzdtt
z
z
======
+
+
2
2
2
1
2
lnlntg.
2
(1)
z
z
dzdzt
zCC
z
z
+
===+=+
+⋅
∫∫
Заменяем t на
arctg
x
и применяем формулу
sin
tg.
21cos
tt
t
=
+
222
tgtgarctg
sin,
1tg1tgarctg1
txx
t
txx
===
+++
222
111
cos,
1tg1tgarctg1
t
txx
===
+++
2
2
2
1
1
1
tg.
2
11
1
x
x
x
tx
x
+
+
==
++
+
70
Приходим к ответу:
2
2
11
lntglnln
2
11
txx
CCC
x
x
++
+=+=−+=
++
2
11
ln.
x
C
xx
+
=−++
2-й способ. Применим подстановку
1
.
x
t
=
Тогда
2
,
dt
dx
t
=−
1
.
t
x
=
Получаем интеграл
2
2
22
2
2
2
11
1
1
ln1
11
1111
ln1ln.
t
t
dxdtdt
tt
t
xxt
x
CC
xxx
x
+
−
=⋅=−=−++=
++
+
=−+++=−++
∫∫∫
4) Выделим полный квадрат в квадратном трехчлене
222
25214(1)4.
xxxxx
++=+++=++
Положим
1,
xy
+=
тогда
,
dxdy
= получаем интеграл
2525
,
(25)(4)
dy
dx
xxy
=
+++
∫∫
для вы-
числения которого применим тригонометрическую подстановку
2tg,
yt
=
2
2
,
cos
dt
dy
t
=
arctg.
2
y
t =
Тогда имеем:
2
2552525
42
2
1
cos
122
cos
(44tg)2(1tg)cos
2cos
t
dtdtdt
t
ttt
t
⋅===
++
∫∫∫
32
2
5
1
cos
111
coscos
161616
cos
t
dt
tdtcosttdt
t
====
∫∫∫
3
2
1sinsin
(1sin)sin.
161648
tt
tdtC
=−=−+
∫
Заменяем
1
arctgarctg:
22
y
x
t
+
==
()
222
2
11
22
1
1
2
2
tgarctg
tg1
sin
1tg
41
1tgarctg
1
xx
x
x
tx
t
t
x
++
+
+
+
=====
+
++
+
+
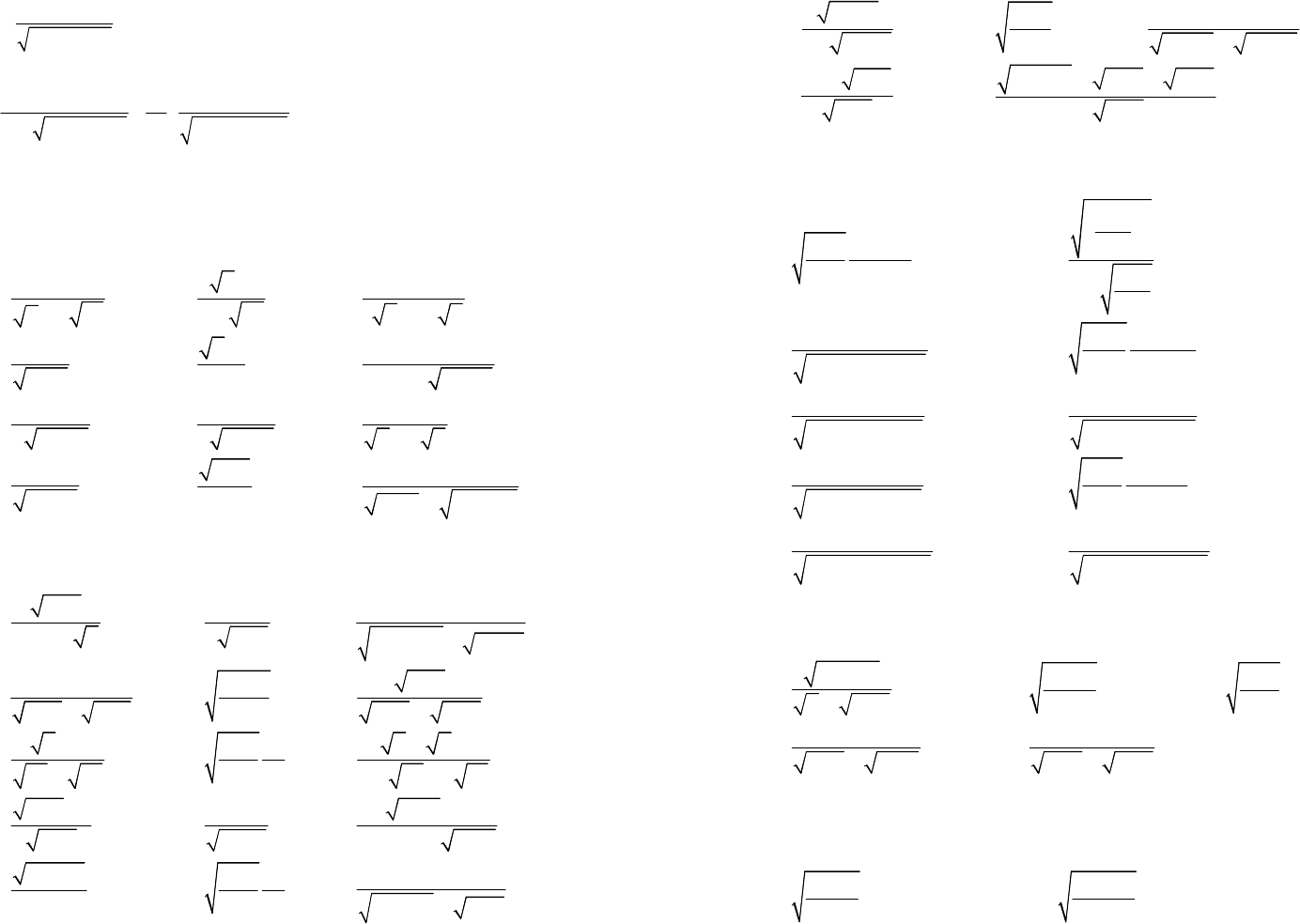
71
2
1
.
25
x
xx
+
=
++
Приходим к ответу:
( )
3
22
1
11
.
48
1625(25)
x
x
C
xxxx
+
+
−+
++++
Задания
I уровень
1.1. Найдите неопределенной интеграл:
1)
3
;
2
dx
xx
+
∫
2)
3
3
2
;
xdx
xx
−
∫
3)
( )
3
;
9
dx
xx
+
∫
4)
3
;
2
x
dx
x −
∫
5)
;
5
xdx
x
+
∫
6)
2
;
(32)32
xdx
xx
++
∫
7)
;
54
dx
xx
−
∫
8)
;
29
dx
xx
+
∫
9)
6
;
2
dx
xx
+
∫
10)
1
;
23
x
dx
x
+
+
∫
11)
1
;
x
dx
x
+
∫
12)
3
.
2(2)
dx
xx+++
∫
II уровень
2.1. Найдите неопределенный интеграл:
1)
2
1
;
(1)
x
dx
xx
+
+
∫
2)
3
;
1
dx
xx
−
∫
3)
( )
2
3
;
2323
dx
xx
+++
∫
4)
3
;
11
xdx
xx
+++
∫
5)
4
;
12
x
dx
x
−
−
∫
6)
6
3
1
;
11
x
dx
xx
−
−+−
∫
7)
6
63
52
2
;
x
dx
xx
−
+
∫
8)
1
;
1
xdx
xx
−
+
∫
9)
36
3
43
21
;
2
xx
dx
xxx
++
+−
∫
10)
3
11
;
1
x
dx
x
++
+
∫
11)
3
;
31
xdx
x
−
∫
12)
2
23
;
(2)2
x
dx
xx
++
+−+
∫
13)
316
;
x
dx
x
−
∫
14)
1
;
1
xdx
xx
+
−
∫
15)
2
3
;
(1)1
dx
xx
+−+
∫
72
16)
3
3
21
;
121
x
dx
x
+
++
∫
17)
1
;
5
x
dx
x
−
−
∫
18)
4
;
3232
dx
xx
−−−
∫
19)
2
3
1
;
1
xx
dx
x
++
+
∫
20)
2
6
3
3
(1)11
.
(1)(11)
xxx
dx
xx
−+−−−
−−+
∫
2.2. Найдите неопределенный интеграл, преобразовав по-
дынтегральную функцию к виду (19.31):
1)
3
2
1
;
1
(1)
xdx
x
x
−
+
+
∫
2)
3
1
1
;
x
x
x
x
dx
x
−
−
+
∫
3)
3
4
;
(2)(2)
dx
xx
+−
∫
4)
2
2
;
2
(2)
xdx
x
x
−
+
−
∫
5)
2
3
;
(1)(2)
dx
xx−+
∫
6)
2
3
;
(1)(1)
dx
xx−+
∫
7)
3
;
(1)(2)
dx
xx−−
∫
8)
3
3
1
;
1
(1)
xdx
x
x
+
−
−
∫
9)
24
3
;
(1)(3)
dx
xx+−
∫
10)
35
4
.
(2)(1)
dx
xx−+
∫
2.3. Найдите интеграл, избавившись от иррациональности в
числителе или знаменателе дроби:
1)
(1)
;
1
xx
dx
xx
+
++
∫
2)
52
;
52
x
dx
x
+
−
∫
3)
1
;
1
x
dx
x
+
−
∫
4)
;
12
dx
xx
−−−
∫
5)
.
11
dx
xx
+−−
∫
2.4. Найдите интеграл (после подстановки вместо разложе-
ния на простейшие дроби примените метод интегрирования по
частям):
1)
54
;
49
x
dx
x
−
+
∫
2)
2
;
925
x
dx
x
−
−
∫
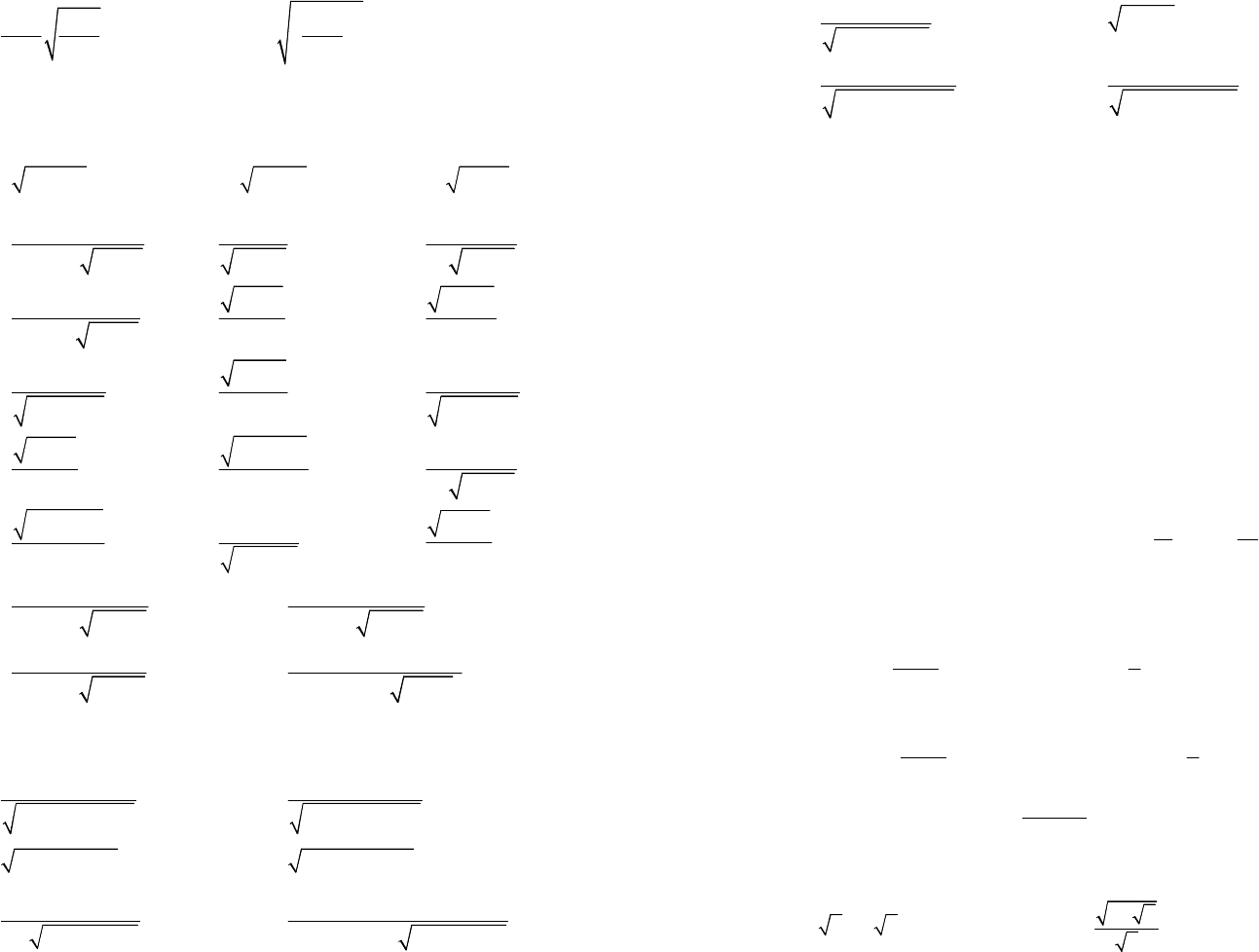
73
3)
11
;
11
xx
dx
xx
++
−−
∫
4)
3
1
.
1
x
dx
x
−
+
∫
III уровень
3.1. Найдите интеграл, применяя тригонометрические под-
становки:
1)
2
16;
xdx
−
∫
2)
22
4;
xxdx
−
∫
3)
32
1;
xxdx
+
∫
4)
22
;
(4)1
dx
xx
+−
∫
5)
2
2
;
5
x
dx
x −
∫
6)
22
;
9
dx
xx
+
∫
7)
22
;
(1)1
dx
xx
−−
∫
8)
2
4
1
;
x
dx
x
−
∫
9)
2
2
2
;
x
dx
x
+
∫
10)
2
23
;
(2)
x
dx
x +
∫
11)
2
4
3
;
x
dx
x
+
∫
12)
4
23
;
(7)
xdx
x−
∫
13)
2
3
1
;
x
dx
x
−
∫
14)
23
6
(1)
;
x
dx
x
−
∫
15)
22
;
9
dx
xx
+
∫
16)
23
6
(9)
;
x
dx
x
−
∫
17)
2
2
;
25
x
dx
x−
∫
18)
2
3
1
;
x
dx
x
−
∫
19)
22
;
(4)4
dx
xx
−+
∫
20)
22
;
(4)4
dx
xx
++
∫
21)
22
;
(9)9
dx
xx
−−
∫
22)
22
.
(1)(1)
dx
xxx
+++
∫
3.2. Найдите интеграл, выделив предварительно в подкорен-
ном выражении полный квадрат:
1)
23
;
(25)
dx
xx++
∫
2)
23
;
(68)
dx
xx++
∫
3)
2
217;
xxdx
−+
∫
4)
2
1021;
xxdx
−−
∫
5)
2
;
122
dx
xx
+−+
∫
6)
22
(4)
;
(24)25
x
dx
xxxx
+
++++
∫
74
7)
2
2
;
32
x
dx
xx−−
∫
8)
2
;
xxdx
−
∫
9)
22
;
(82)
dx
xx+−
∫
10)
2
(2)
.
1029
xdx
xx
+
−+
∫
19.8. Интегралы от дифференциальных биномов
Дифференциальным биномом называется выражение вида
(),
mnp
xabxdx
+ (19.32)
где m, n, p – рациональные числа; a, b – действительные чис-
ла, отличные от нуля.
Если
,
p
∈
N
то можно использовать формулу бинома Нью-
тона, и этим сводим интеграл к интегралу от степенной функ-
ции. В общем случае интегралы от дифференциальных биномов,
т. е.
(),
m
np
xabxdx
+
∫
можно привести к интегралу от рацио-
нальной функции в следующих трех случаях:
1) если p – целое число,
1
1
,
r
m
s
=
2
2
,
r
n
s
=
12
,,
rr
∈
Z
22
,,
ss
∈
N
то применяется подстановка
,
s
xt
=
где
12
(,);
s
НОК ss
=
2) если
1
m
n
+
– целое число,
,
r
p
s
=
,
r
∈
Z
,
s
∈
N
то приме-
няется подстановка
;
ns
abxt
+=
3) если
1m
p
n
+
+
– целое число,
,
r
p
s
=
,
r
∈
Z
,
s
∈
N
то
применяется подстановка
.
n
ns
n
abx
axbt
x
−
+
=+=
Пример 1. Найти неопределенный интеграл:
1)
2
3
(1);
xxdx
+
∫
2)
3
6
1
;
x
dx
x
+
∫
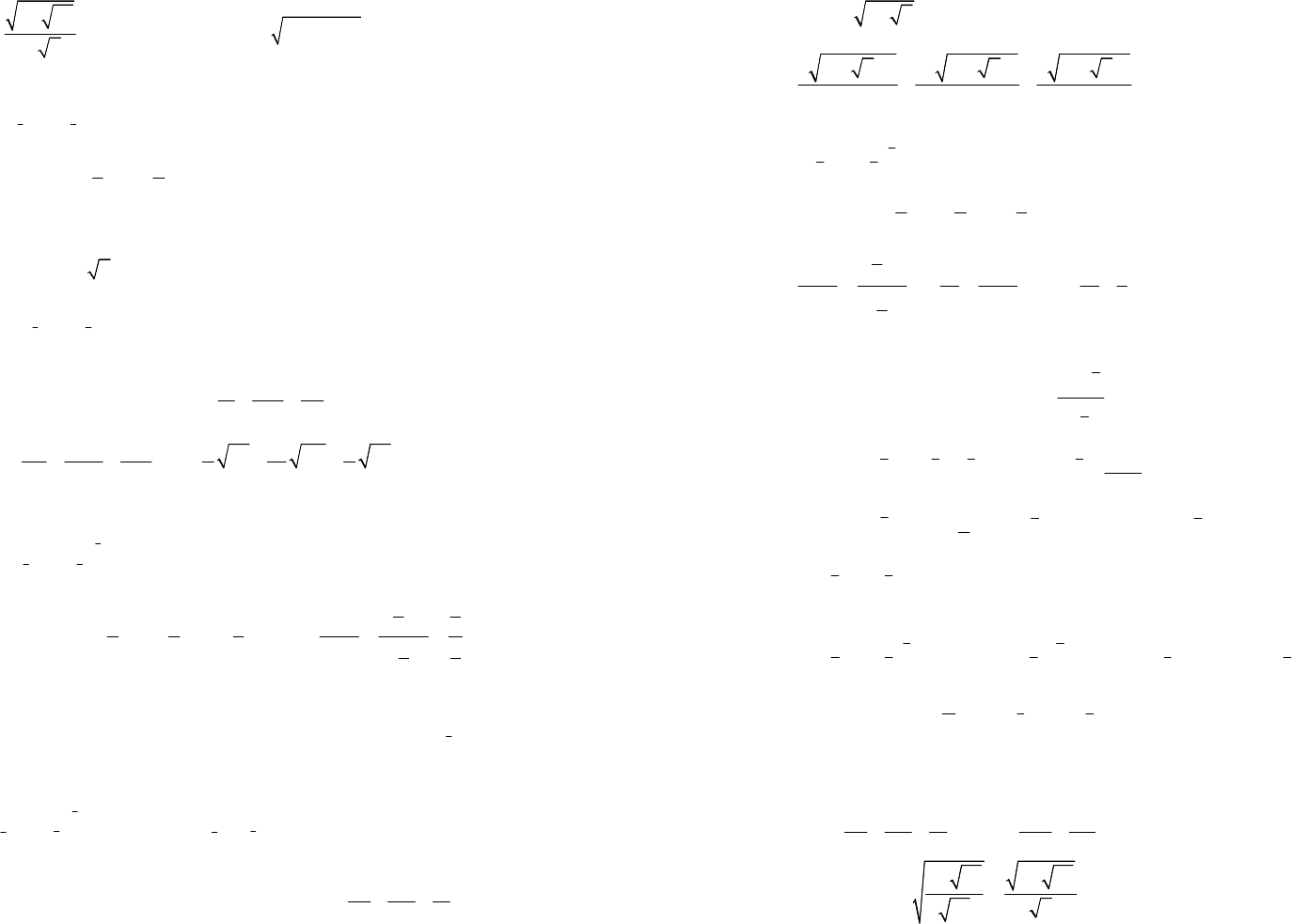
75
3)
3
4
3
3
1
;
x
dx
xx
+
∫
4)
3
(29).
xxdx
+
∫
Решение. 1) Запишем подынтегральную функцию в виде диффе-
ренциального бинома (19.32)
(
)
1 1
3
2
2
1.
xx+
Тогда
1
,
3
m
=
1
,
2
n
=
2,
p
=
т. е. p – целое число. Следовательно,
имеем первый случай интегрируемости дифференциального бинома.
Так как
(3,2)6,
НОК
=
то применим подстановку
6
.
xt
=
Тогда
5
6,
dxtdt
=
6
.
tx
=
Вычисляем:
(
)
1
1
3 2
2
2325736
1(1)66(12)
xxdxtttdttttdt
+=+⋅=++=
∫∫∫
( )
81114
71013
2
626
81114
ttt
tttdtC
=++=+++=
∫
81114
363
4117
31233123
.
41174117
ttt
CxxxC
=+++=+++
2) Запишем подынтегральную функцию в виде дифференциально-
го бинома (19.32)
(
)
1
3
1
1
62
1.
xxdx
−
+
Тогда
1
,
2
m
=−
1
,
6
n
=
1
,
3
p
=
3,
s
=
11
22
11
66
1
1
3
m
n
−+
+
===
– це-
лое число.
Следовательно, здесь мы имеем второй случай интегрируемости
дифференциального бинома. Используем подстановку
1
6
3
1.
xt
+=
Тогда
36
(1),
xt=−
352235
6(1)318(1).
dxttdtttdt
=−⋅=−
(
)
1
3
11
11
6322
363235323
1((1))()18(1)18(1)
xxdxttttdtttdt
−−
+=−−=−=
∫∫∫
1074
633963
2
18(21)18(2)18,
1074
ttt
tttdttttdtC
=−+=−+=−++
∫∫
76
где
3
6
1.
tx
=+
Получаем ответ:
1074
666
333
9(1)36(1)9(1)
.
572
xxx
C
+++
−++
3) Запишем подынтегральную функцию в виде (19.32)
( )
1
73
3
24
1.
xxdx
−
+
Тогда
7
,
2
m
=−
3
,
4
n
=
1
,
3
p
=
3.
s
=
7
2
3
4
1
110
,
3
m
n
−+
+
==−
1101
3
33
m
p
n
+
+=−+=−
– целое число. Сле-
довательно, имеем третий случай интегрируемости дифференциально-
го бинома. Используем подстановку
3
4
3
3
4
1
.
x
t
x
+
=
Тогда
33
3
44
1,
xtx
+=
3
3
4
(1)1,
xt
−=
3
31
4
3
1
(1),
1
xt
t
−
==−
−
4
3
3
(1),
xt
−
=−
77
3223
33
4
(1)34(1).
3
dxttdtttdt
−−
=−−=−−
33
3331
44
1(1).
xtxtt
−
+==−
Переходя в подынтегральном выражении к переменной t, получаем:
( )
( )
( )
1 7
47
73
1
3 2
333123
33
24
3
1(1)(1)(4)(1)
xxdxtttttdt
−
−−
−
−
+=−−−−=
∫∫
1417
2333332
333
(4)(1)(1)(1)4(1)
tttttdtttdt
−−
=−−−−=−−=
∫∫
363963
4(21)4(2)
tttdttttdt
=−−+=−−+=
∫∫
1074107
4
228
4.
107457
ttttt
CtC
=−−++=−+−+
Заменяем t на
3
44
33
3
4
4
3
11
xx
x
x
++
=
и получаем ответ:
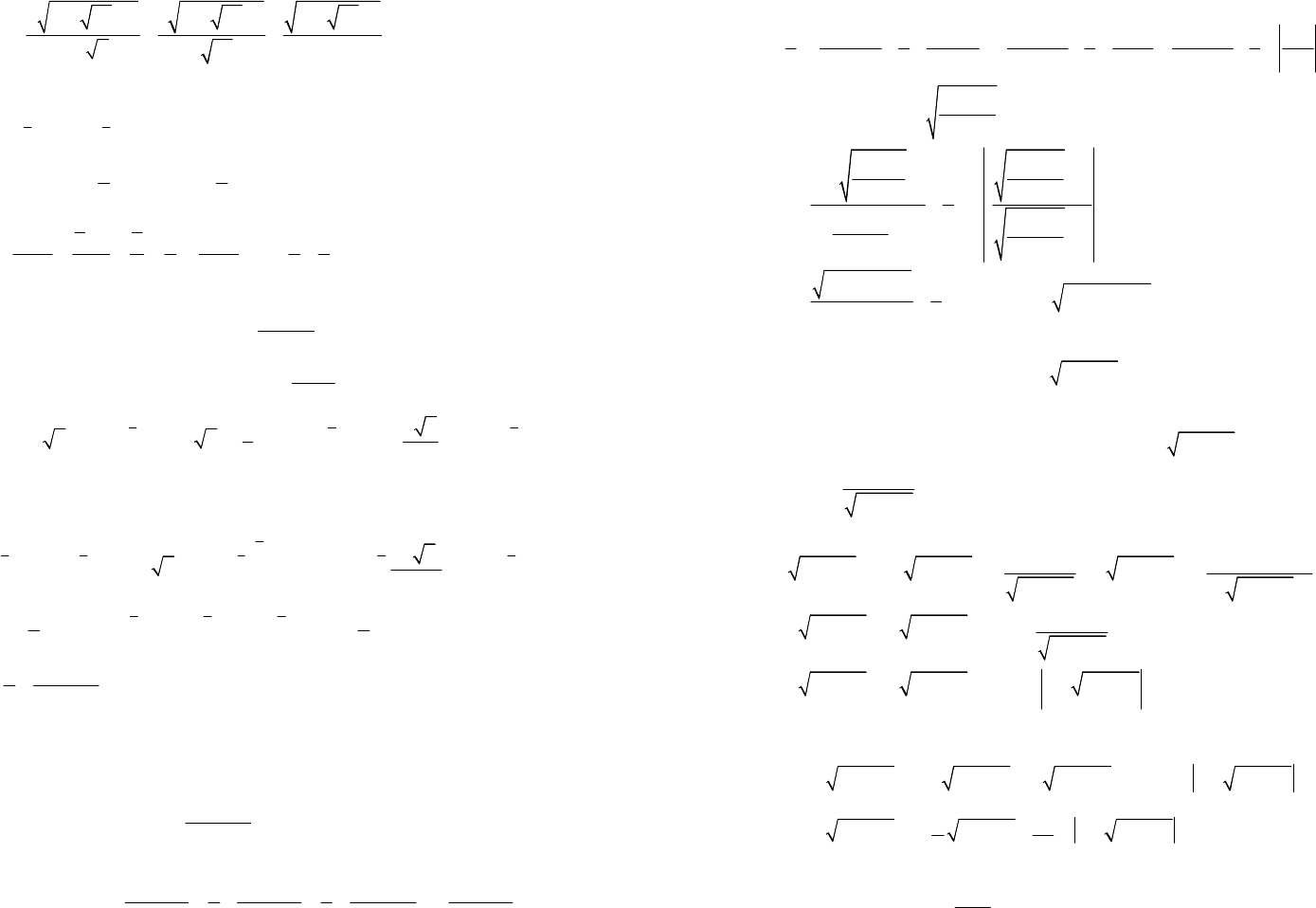
77
444
333
3103734
2
4
3
2(1)8(1)(1)
.
5
xxx
C
x
xx
xx
+++
−+−+
4) Запишем подынтегральную функцию в виде дифференциально-
го бинома (19.32)
11
3
22
(29).
xx+
Тогда
1
,
2
m =
3,
n
=
1
,
2
p =
2.
s
=
13
22
1
11
,
332
m
n
+
+
===
111
1
22
m
p
n
+
+=+=
– целое число. Следо-
вательно, имеем третий случай интегрируемости дифференциального
бинома. Используем подстановку:
3
2
3
29
.
x
t
x
+
=
Тогда
323
29,
xtx
+=
32
(9)2,
xt
−=
( )
1
32
2
2
29,
9
xt
t
−
==−
−
1
2
3
3
2(9),
xt
−
=−
44
3
22
3
33
122
2(9)2(9).
33
dxttdtttdt
−−
=−−=−−
3221
292(9).
xtt
−
+=−
Интеграл преобразуется к виду
( )
1
14
111
3
2
322212
3
33
222
22
(29)2(9)(2(9))(9)
3
t
xxdxttttdt
−−
−
−
+=−−−=
∫∫
141
2
222222
63
2
2
22
44
(9)(9)(9)(9)
33
4
.
3
(9)
ttttdtttdt
t
dt
t
−
−−
−
=−−−−=−−=
=−
−
∫∫
∫
Последний интеграл можно вычислить двумя способами: либо
разложить подынтегральную рациональную дробь на сумму простей-
ших дробей либо применить формулу интегрирования по частям.
Вычислим 2-м способом.
Положим
,
ut
=
22
.
(9)
tdt
dv
t
=
−
Тогда
,
dudt
=
2
2222222
(9)
1211
.
22
(9)(9)(9)2(9)
dt
tdttdt
v
tttt
−
====−
−−−−
∫∫∫
78
Получим:
22222
4122213
ln.
32393
2(9)(9)3(9)93(9)
tdttdttt
C
t
ttttt
−
−−+=−=−+
+
−−−−−
∫∫
Заменяем t на
3
3
29
x
x
+
и окончательно получаем:
33
33
3
3
3
3
29
29
32
1
ln
9
29
29
39
3
x
x
x
x
C
x
x
x
x
+
+
−
−+=
+
+
−
+
(
)
33
333
(29)
1
ln913(29).
39
xx
xxxC
+
−+−++
Пример 2. Найти интеграл
2
25
xdx
−
∫
разными способами.
Решение. 1-й способ. Для вычисления интеграла используем фор-
мулу интегрирования по частям. Положим
2
25,
ux=−
.
dvdx
=
То-
гда
2
,
25
xdx
du
x
=
−
.
vx
=
Имеем:
22
222
22
(25)25
252525
2525
xdxx
xdxxxxxdx
xx
−+
−=−−=−−=
−−
∫∫∫
22
2
252525
25
dx
xxxdx
x
=−−−−=
−
∫∫
222
252525ln25.
xxxdxxx=−−−−+−
∫
В правой части этого равенства получили исходный интеграл.
Найдем его из уравнения
2222
25252525ln25.
xdxxxxdxxx−=−−−−+−
∫∫
222
25
2525ln25.
22
x
xdxxxxC
−=−−+−+
∫
2-й способ. Для вычисления интеграла применим тригонометриче-
скую подстановку
5
.
cos
x
t
=
