Майсеня Л.И. Математика в примерах и задачах. Часть 4
Подождите немного. Документ загружается.

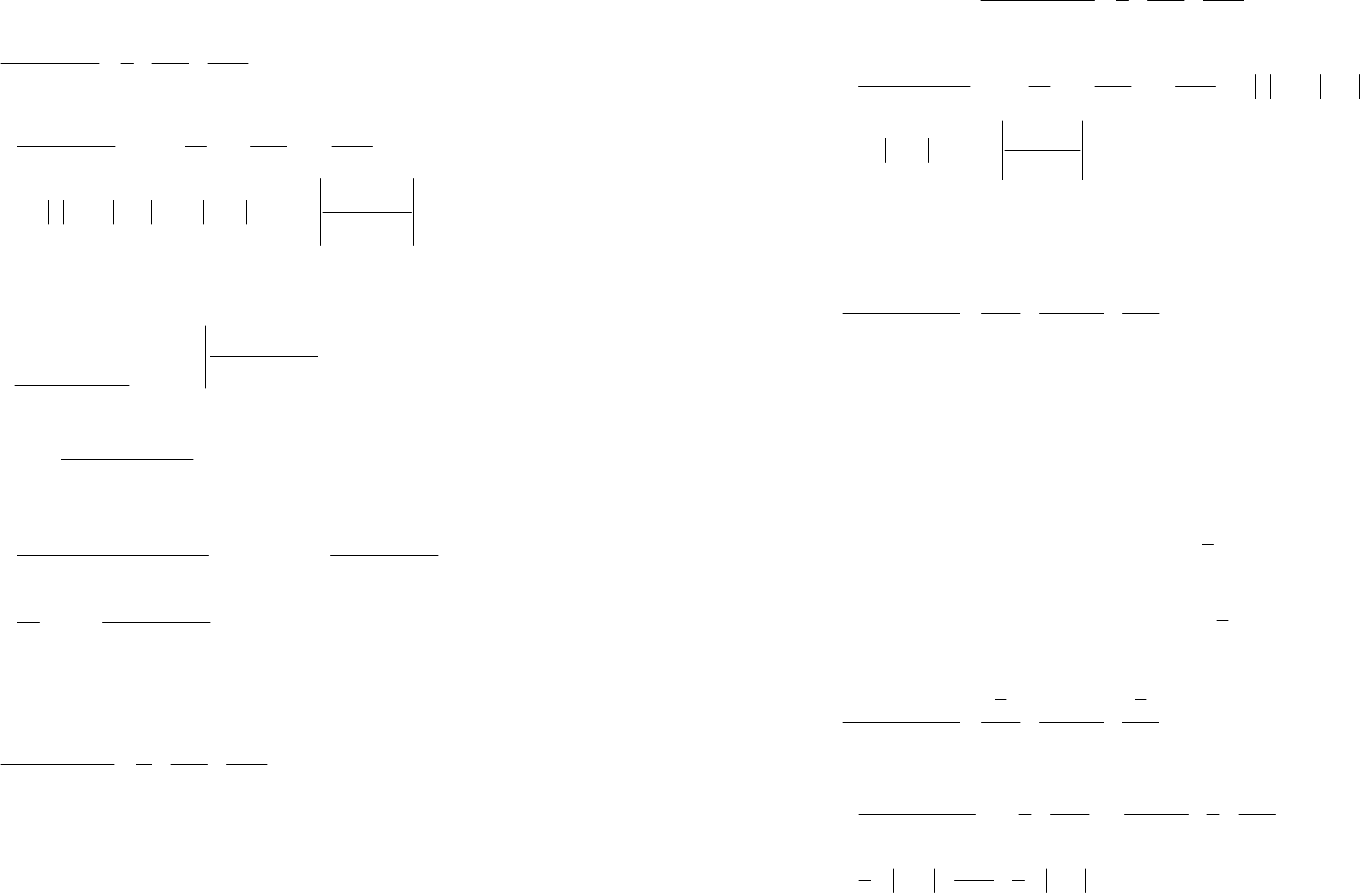
39
1;
26;
24.
ABC
ABC
A
++=
+−=−
−=−
Решая ее, находим
2,
A
=
3,
B
=−
С = 2. Таким образом,
2
32
64232
.
12
2
xx
xxx
xxx
−−
=−+
−+
+−
Значит,
2
32
64
232
12
2
xxdxdxdx
dx
xxx
xxx
−−
=−+=
−+
+−
∫∫∫∫
( )
( )
2
2
3
2
2ln3ln12ln2ln.
1
xx
xxxCC
x
+
=−−+++=+
−
2) Подынтегральная функция является неправильной дробью. Пу-
тем деления числителя на знаменатель выделим целую часть рацио-
нальной дроби и правильную рациональную дробь:
432
32
432
32
32
2
61034
54
1
54
634
54
74
xxxx
xxx
x
xxx
xxx
xxx
xx
++−+
++
−
+
++
+−+
−
++
−+
Тогда
4322
3232
6103474
1
5454
xxxxxx
dxxdx
xxxxxx
++−+−+
=++=
++++
∫∫
22
32
74
.
2
54
xxx
xdx
xxx
−+
=++
++
∫
Разложим на множители знаменатель правильной дроби:
(
)
(
)
32
5414.
xxxxxx++=++
Имеем:
2
74
,
(1)(4)14
xxABC
xxxxxx
−+
=++
++++
откуда
2
74(1)(4)(4)(1).
xxAxxBxxCxx
−+=++++++
Найдем коэффициенты методом частных значений. В последнем
равенстве, полагая последовательно
0,
x
=
1,
x
=−
4,
x
=−
получаем
40
соответственно:
44,
A
=
123,
B
=−
4812,
C
=
т. е.
1,
A
=
4,
B
=−
4.
C
=
Следовательно,
2
44
741
.
(1)(4)14
xx
xxxxxx
−+
=−+
++++
Поэтому
2
74
44ln4ln1
(1)(4)14
xxdxdxdx
dxxx
xxxxxx
−+
=−+=−++
++++
∫∫∫∫
4
4
(4)
4ln4ln.
(1)
xx
xCC
x
+
+++=+
+
3) Знаменатель подынтегрального выражения имеет корень
3,
x
=
кратности 2, и простой корень
1.
x
=−
Общий вид разложения на про-
стейшие дроби подынтегральной функции в данном случае будет
иметь вид:
( )( ) ( )
2
22
8
.
31
313
xxABC
xx
xxx
+−
=++
−+
−+−
Приведем правую часть этого равенства к общему знаменателю и
приравняем числители:
( )( ) ( ) ( )
2
2
83113,
xxAxxBxCx+−=−++++−
(
)
(
)
22
82639.
xxACxABCxABC
+−=++−+−−++
Приравняв коэффициенты при одинаковых степенях переменной x,
получаем систему уравнений, решая которую, находим коэффициенты:
1,
261,
398;
AC
ABC
ABC
+=
−+−=
−++=−
3
,
2
1
.
2
1,
A
B
C
=
=
=−
Таким образом имеем разложение:
( )( ) ( )
2
22
31
22
81
.
31
313
xx
xx
xxx
+−
=+−
−+
−+−
Тогда
( )( ) ( )
2
22
831
2321
313
xxdxdxdx
dx
xx
xxx
+−
=+−=
−+
−+−
∫∫∫∫
311
ln3ln1.
232
xxC
x
=−−−++
−
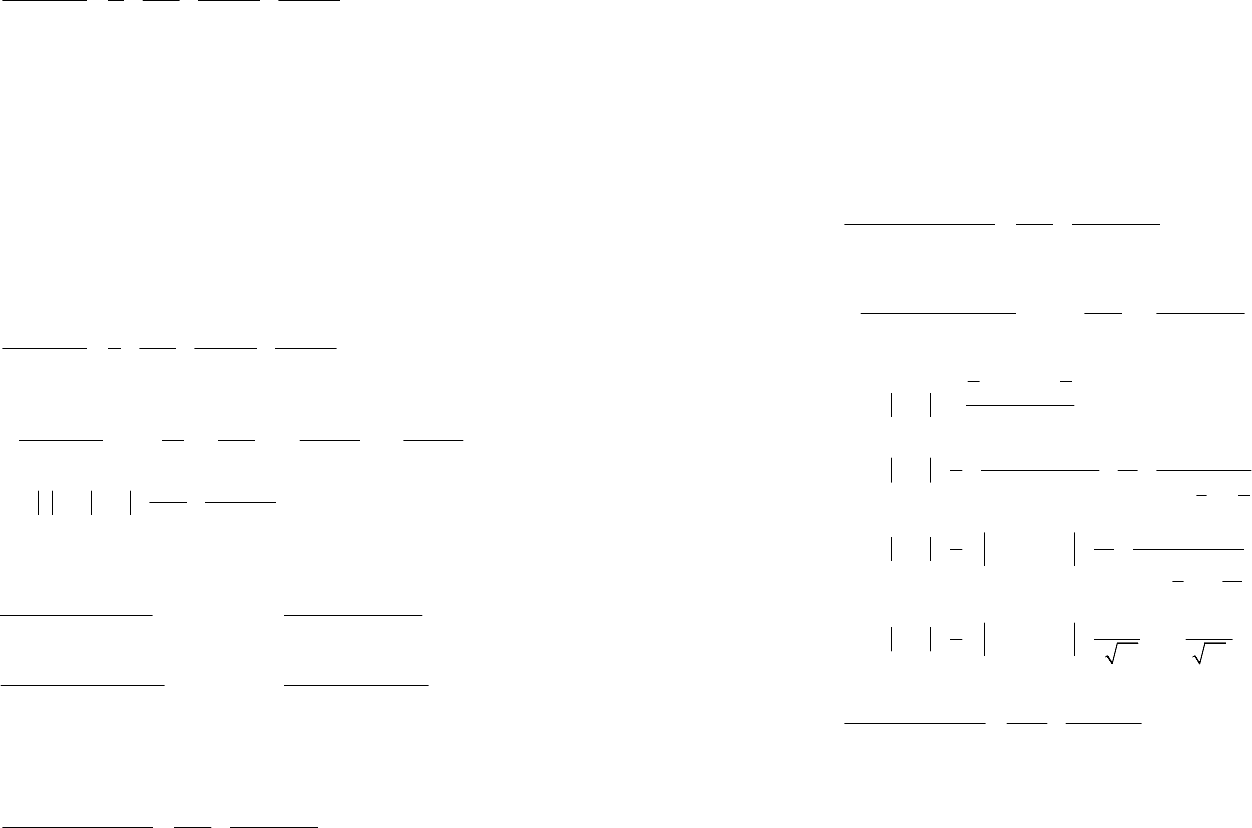
41
4) Знаменатель подынтегрального выражения имеет простой ко-
рень
0,
x
=
которому соответствует простейшая дробь I типа, и корень
1
x
=
кратности 3, которому соответствует сумма трех простейших
дробей I и II типов. Имеем:
( ) ( ) ( )
2
323
31
.
1
111
xxABCD
xx
xxxx
−−
=+++
−
−−−
Приведем правую часть этого равенства к общему знаменателю и
приравняем числители:
( ) ( ) ( )
32
2
31111.
xxAxBxxCxxDx
−−=−+−+−+
Найдем коэффициенты методом частных значений. Полагая
0,
x
=
получаем:
1,1.
AA
−=−=
При
1
x
=
имеем:
3.
D
=−
Найдем производную от обеих частей последнего равенства:
( ) ( ) ( ) ( )
22
23311211.
xAxBxBxxCxCxD
−=−+−+−+−++
Полагая
1,
x
=
получаем:
1,2.
CDC
−=+=
При
0
x
=
имеем:
33,
ABCD
−=+−+
1.
B
=−
Таким образом,
( ) ( ) ( )
2
323
311123
.
1
111
xx
xx
xxxx
−−
=−+−
−
−−−
Тогда
2
323
31
23
1
(1)(1)(1)
xxdxdxdxdx
dx
xx
xxxx
−−
=−+−=
−
−−−
∫∫∫∫∫
2
23
lnln1.
1
2(1)
xxC
x
x
=−−−++
−
−
Пример 2. Вычислить неопределенный интеграл:
1)
( )
( )
2
2
145
.
132
xx
dx
xxx
++
+−+
∫
2)
2
2
7
;
(2)(1)
x
dx
xxx
−
−−+
∫
3)
32
22
36115
;
(1)(22)
xxx
dx
xxx
+++
+++
∫
4)
22
.
(1)(1)
xdx
xxx+++
∫
Решение. 1) Поскольку квадратный трехчлен
2
32
xx
−+
не имеет
действительных корней, то приходим к следующему общему виду раз-
ложения подынтегральной функции на простейшие дроби:
2
22
145
.
1
(1)(32)32
xxABxC
x
xxxxx
+++
=+
+
+−+−+
42
Приведение правой части к общему знаменателю и приравнивание
числителей дает уравнение:
22
145(32)()(1),
xxAxxBxCx
++=−++++
т. е.
22
145(3)()2.
xxABxABCxAC
++=++−++++
Приравняв коэффициенты при одинаковых степенях x, получаем
систему уравнений
314,
1,
25.
AB
ABC
AC
+=
−++=
+=
Решая полученную систему, находим коэффициенты:
3,
A
=
5,
B
=
1.
C
=−
Таким образом,
2
22
145351
.
1
(1)(32)32
xxx
x
xxxxx
++−
=+
+
+−+−+
Следовательно,
( )
( )
2
2
2
14551
3
1
32
132
xxdxx
dxdx
x
xx
xxx
++−
=+=
+
−+
+−+
∫∫∫
()
( )
2
2
2
2
12
33
51
61
66
3ln1
32
32
51
3ln1
618
32
x
xdx
xx
dxx
dx
x
xx
xx
−−
=++=
−+
−+
=++−=
−+
−+
∫
∫∫
2
2
123
636
51
3ln1ln32
618
dx
xxx
x
=++−+−=
−+
∫
2
5161
3ln1ln32arctg.
6
32323
x
xxxC
−
=++−+−+
2) Имеем:
2
22
7
,
2
(2)(1)1
xABxC
x
xxxxx
−+
=+
−
−−+−+
откуда
22
7(1)(2)().
xAxxxBxC
−=−++−+
Для нахождения неизвестных коэффициентов применим одновре-
менно метод частных значений и метод неопределенных коэффициен-
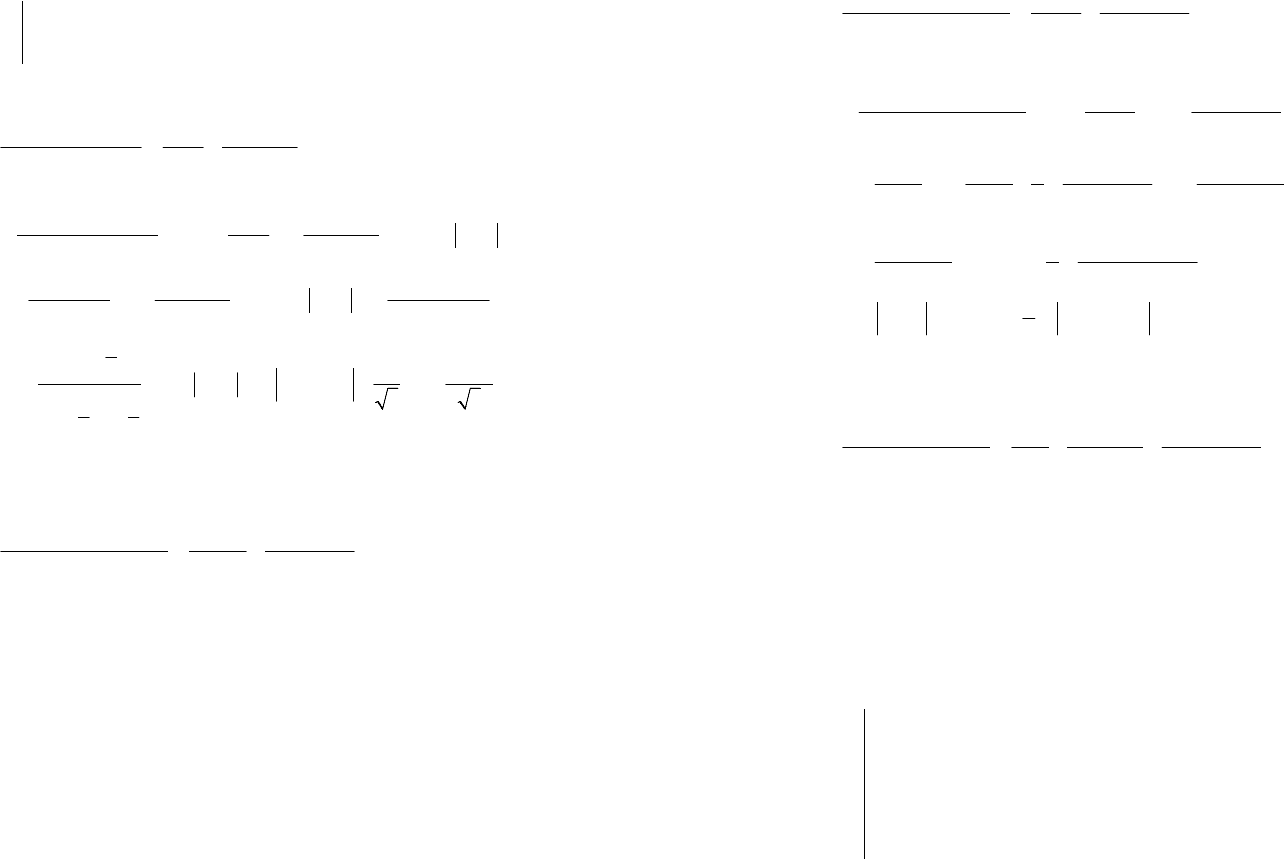
43
тов. Подставляя
2,
x
=
находим:
33,
A
−=
1.
A
=−
Для нахождения коэффициентов B и C достаточно приравнять ко-
эффициенты при x
2
и x
0
:
2
0
1,
27.
x
AB
AC
x
+=
−=−
Из последней системы уравнений получаем:
2,
B
=
3.
C
=
Таким образом,
2
22
7123
.
2
(2)(1)1
xx
x
xxxxx
−−+
=+
−
−−+++
Тогда
2
22
723
ln2
2
(2)(1)1
xdxx
dxdxx
x
xxxxx
−+
=−+=−−+
−
−−+++
∫∫∫
2
222
(21)(1)
2ln2
111
xdxdxdxx
dxx
xxxxxx
+++
++=−−++
++++++
∫∫∫
2
2
1
2
13
24
421
2ln2ln1arctg.
33
dx
x
xxxC
x
+
+
+=−−+++++
++
∫
3) Поскольку квадратные трехчлены
2
1
x
+
и
2
22
xx
++
не имеют
действительных корней, то приходим к следующему общему виду раз-
ложения подынтегральной функции на сумму простейших дробей:
( )( )
32
22
22
36115
.
122
122
xxxAxBCxD
xxx
xxx
+++++
=+
+++
+++
Приводим правую часть этого равенства к общему знаменателю и
приравниваем числители. Получаем уравнение
( )
(
)
( )
(
)
( ) ( )
( )
3222
3232
36115221;
361152
222.
xxxAxBxxCxDx
xxxACxABDx
ABCxBD
+++=++++++
+++=+++++
+++++
Приравняв коэффициенты при одинаковых степенях переменной х,
получаем систему уравнений
3,
26,
2211,
25.
AC
ABD
ABC
BD
+=
++=
++=
+=
44
Решая полученную систему, находим коэффициенты:
2,
A
=
3,
B
=
1,
C
=
1.
D
=−
Таким образом,
( )( )
32
22
22
36115231
.
122
122
xxxxx
xxx
xxx
++++−
=+
+++
+++
Следовательно,
( )( )
( )
( )
( ) ( )
( )
( )
22
22
22
2222
22
22
22
36115231
122
122
22
21
32
2
1122
11
122
1
3arctg2arctg1
2
122
1
ln13arctgln222arctg1.
2
xxxxx
dxdxdx
xxx
xxx
xdx
xdxdxdx
xxxx
x
dxdxx
xx
xxx
xxxxxC
++++−
=+=
+++
+++
+
=++−=
++++
++
+++
=++−+=
+++
=+++++−++
∫∫∫
∫∫∫∫
∫∫
4) В данном случае при разложении подынтегральной функции на
простейшие дроби в качестве слагаемых будем иметь простейшие дро-
би I, III и IV типов:
22222
.
1
(1)(1)1(1)
xABxCDxE
x
xxxxxxx
++
=++
+
+++++++
Отсюда получаем:
222
(1)()(1)(1)()(1).
xAxxBxCxxxDxEx
=++++++++++
Полагая
1,
x
=−
получаем:
1.
A
=−
Приведем подобные члены в
правой части этого равенства:
432
()(22)(322)
xABxABCxABCDx
=+++++++++
(22)().
ABCDExACE
++++++++
Приравнивая коэффициенты при одинаковых степенях перемен-
ной x, получим систему уравнений
4
3
2
1
0
0,
220,
3220,
221,
0.
x
AB
x
ABC
x
ABCD
ABCDEx
ACE
x
+=
++=
+++=
++++=
++=
Из нее находим
1,
B
=
0,
C
=
1,
D
=
1.
E
=
Следовательно,
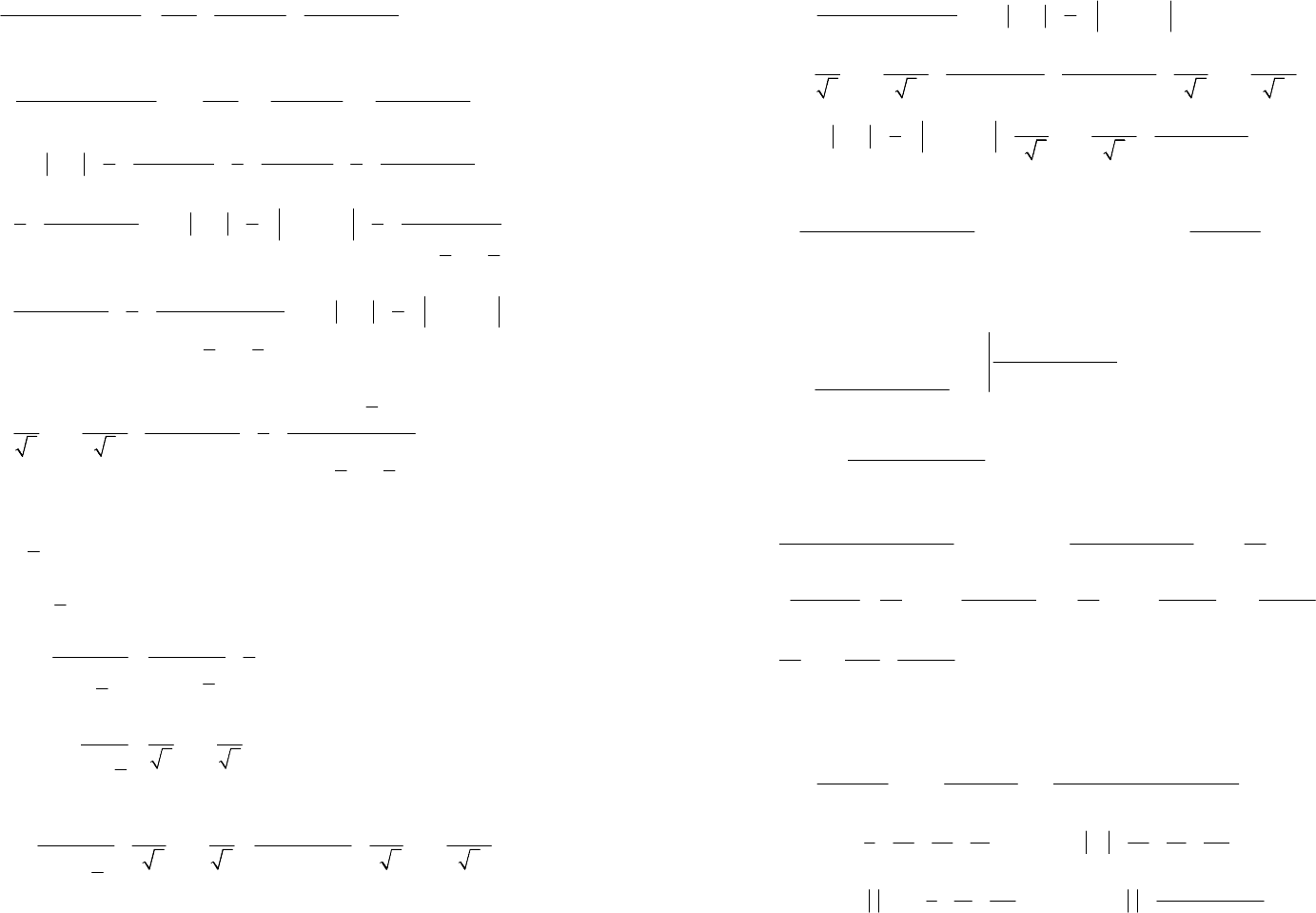
45
22222
11
.
1
(1)(1)1(1)
xxx
x
xxxxxxx
−+
=++
+
+++++++
Тогда
(
)
22222
1
1
(1)(1)1(1)
xdx
dxdxxdx
x
xxxxxxx
+
=−++=
+
+++++++
∫∫∫∫
(
)
2222
21
111(21)
ln1
222
11(1)
xdx
dxxdx
x
xxxxxx
+
+
=−++−++
++++++
∫∫∫
2
222
111
ln1ln1
222
(1)
13
24
dxdx
xxx
xx
x
+=−++++−−
++
++
∫∫
2
22
2
111
ln1ln1
22
2(1)
13
24
dx
xxx
xx
x
−+=−++++−
++
++
∫
22
2
1
12111
2
arctg.
2
332(1)
13
24
dx
x
xx
x
+
+
−−+
++
++
∫
Для нахождения последнего интеграла сделаем замену перемен-
ной
1
2
xt
+=
и применим рекуррентную формулу (19.21) для случая
1,
k
=
2
3
:
4
a =
21
2
2
2
22
,
3
3
3
3
4
4
dtt
II
t
t
==+
+
+
∫
где
1
2
22
arctg.
3
33
4
dtt
I
t
==
+
∫
Тогда получаем:
( )
2
2
2
24221421
arctgarctg.
3
333333
31
3
4
ttxx
I
xx
t
++
=+=+
++
+
Приходим к ответу:
46
2
22
1
ln1ln1
2
(1)(1)
xdx
xxx
xxx
=−++++−
+++
∫
( )
2
2
2
2
121121221
arctgarctg
336(1)333
21
11211
ln1ln1arctg.
2
3333(1)
xxx
xx
xx
xx
xxxC
xx
+++
−−++=
++
++
+−
−++++−++
++
Пример 3. Вычислить интегралы:
1)
432
32
4634
;
331
xxxx
dx
xxx
−+−+
−+−
∫
2)
9
24
2
.
(2)
x
dx
x+
∫
Решение. 1) Подынтегральная функция является неправильной
дробью. Выделим целую часть дроби, разделив ее числитель на знаме-
натель по правилу деления многочленов:
432
32
432
32
32
4634
331
1
33
324
331
3
xxxx
xxx
x
xxxx
xxx
xxx
x
−+−+
−+−
−
−
−+−
−+−+
−
−+−+
+
Тогда
4322
3232
46343
1
2
331331
xxxxxx
dxxdxx
xxxxxx
−+−++
=−+=−+
−+−−+−
∫∫
22
3323
(3)(1)4
4
22
(1)(1)(1)(1)
xdxx
xxdxdx
xdxx
xxxx
+−+
+=−+=−++=
−−−−
∫∫∫∫
2
2
12
.
21
(1)
x
xC
x
x
=−−−+
−
−
2) Сделаем замену
2
2.
xt
+=
Тогда
2,
dtxdx
=
2
2,
xt
=−
98244
22()2(2).
xdxxxdxxxdxtdt
=⋅=⋅=− Получаем интеграл
94432
2444
2(2)8243216
(2)
xtdttttt
dxdt
xtt
−−+−+
===
+
∫∫∫
23423
8243216241616
18ln
3
dtttC
tt
ttttt
=−+−+=−−+−+=
∫
2
233
3228(962)
8ln88ln.
33
tt
ttCttC
t
ttt
−+
=−−−++=−−+
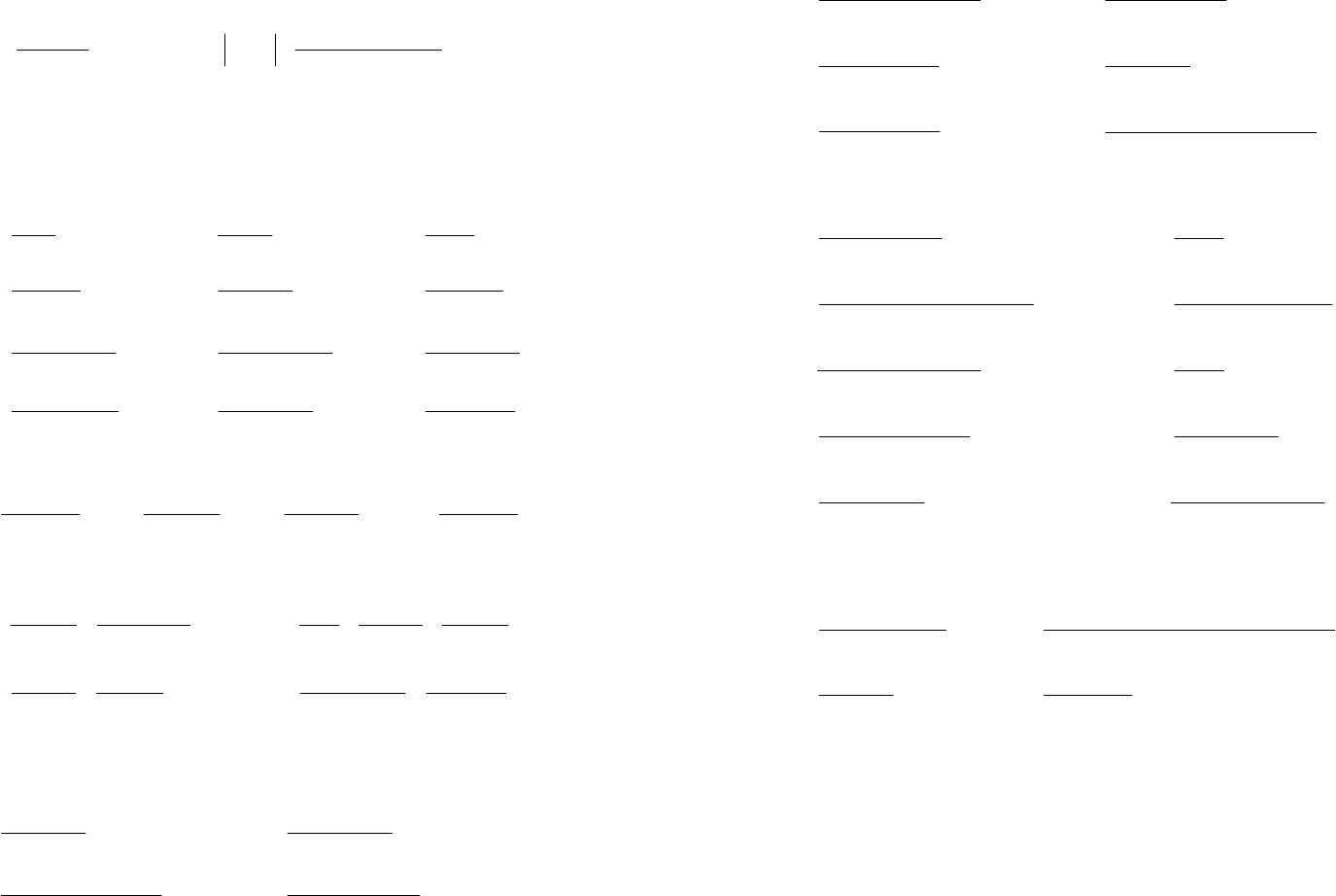
47
Возвращаемся к старой переменной, подставим
2
2
tx
=+
и полу-
чаем:
942
22
2423
28(93022)
28ln2.
(2)3(2)
xxx
dxxxC
xx
++
=+−+−+
++
∫
Задания
I уровень
1.1. Найдите интеграл от простейшей дроби:
1)
;
7
dx
x
−
∫
2)
;
23
dx
x
+
∫
3)
6
;
13
dx
x
−
∫
4)
2
;
(2)
dx
x +
∫
5)
3
;
(21)
dx
x −
∫
6)
6
;
(45)
dx
x
−
∫
7)
2
;
610
dx
xx++
∫
8)
2
;
1034
xdx
xx++
∫
9)
2
41
;
25
x
dx
xx
−
−+
∫
10)
2
23
;
429
x
dx
xx
−
++
∫
11)
2
53
;
34
x
dx
xx
+
++
∫
12)
2
4
.
31
x
dx
xx
+
−+
∫
1.2. Найдите интеграл от простейшей дроби IV типа:
1)
22
;
(4)
dx
x +
∫
2)
23
;
(9)
dx
x +
∫
3)
22
21
;
(1)
x
dx
x
+
+
∫
4)
22
32
.
(4)
x
dx
x
−
+
∫
1.3. Найдите интеграл от простейших дробей:
1)
42
52
;
(3)22
dx
xxx
−
+−+
∫
2)
23
312
;
1
(1)(2)
dx
x
xx
+−
+
++
∫
3)
23
41
;
25(4)
x
dx
xx
−
+−
∫
4)
22
613
.
8202(2)
x
dx
xxx
+
+
++−
∫
II уровень
2.1. Найдите неопределенный интеграл:
1)
2
51
;
2
x
dx
xx
+
+−
∫
2)
2
32
46
;
2
xx
dx
xxx
−−
+−
∫
3)
2
32
;
(1)(56)
x
dx
xxx
+
−−+
∫
4)
42
2
21
.
(1)
xxx
dx
xx
+++
+
∫
48
5)
32
5523
;
(1)(1)(5)
xxx
dx
xxx
−++
−+−
∫
6)
2
2
32
;
(1)(2)
xx
dx
xx
−+
+−
∫
7)
2
3
55
;
(1)(2)
xx
dx
xx
−+
−−
∫
8)
32
;
(1)
dx
xx−
∫
9)
2
4
;
(2)(1)
x
dx
xx
+
++
∫
10)
532
2
111954
;
34
xxxx
dx
xx
−−−+
−+
∫
2.2. Найдите неопределенный интеграл:
1)
3
2
3
;
(3)(9)
xx
dx
xx
++
++
∫
2)
3
;
1
xdx
x
+
∫
3)
22
;
(35)(23)
dx
xxxx−+++
∫
4)
32
22
222
;
(1)(1)
xxx
dx
xxx
+−−
+++
∫
5)
2
22
324
;
(2)(22)
xx
dx
xxx
−+
+++
∫
6)
4
;
1
dx
x
−
∫
7)
42
2
3311
;
(1)(4)
xxx
dx
xx
+−−
−+
∫
8)
3
42
371
;
56
xx
dx
xx
++
++
∫
9)
42
3
;
69
x
dx
xx
+
++
∫
10)
432
42
327
.
54
xxxx
dx
xx
−++−
++
∫
III уровень
3.1. Найдите неопределенный интеграл:
1)
22
;
(1)(1)
xdx
xx++
∫
2)
5432
222
2311181632
;
(4)
xxxxx
dx
xx
−+−+−
+
∫
3)
5
24
;
(1)
x
dx
x+
∫
4)
7
24
32
.
(32)
x
dx
x+
∫
19.6. Интегрирование тригонометрических выражений
Для вычисления интегралов вида
sin()cos(),
axbcxddx
++
∫
cos()cos(),
axbcxddx
++
∫
sin()sin(),
axbcxddx
++
∫
где a, b, c, d –
49
действительные числа, применяют следующие тригонометриче-
ские формулы:
1
coscos(cos()cos()),
2
1
sinsin(cos()cos()),
2
1
sincos(sin()sin()),
2
αβαβαβ
αβαβαβ
αβαβαβ
=−++
=−−+
=−++
(19.22)
с помощью которых произведение тригонометрических функций
переводится в сумму.
Вычисление интеграла вида
sincos
mn
xxdx
∫
(19.23)
зависит от показателей степеней m и n.
Рассмотрим следующие случаи:
1. Если в формуле (19.23) m – нечетное положительное чис-
ло, т. е.
21,
mk
=+
,
k
∈
N
то подынтегральное выражение пре-
образуется следующим образом:
21222
sinsinsinsin(sin)sin(1cos)sin.
mkkkk
xxxxxxxx
+
====−
Делают это с целью поднесения под знак дифференциала.
Тогда
212
sincos(1cos)cossin
knkn
xxdxxxxdx
+
=−=
∫∫
22
(1cos)cos(sin)(1cos)cos(cos).
knkn
xxxdxxxdx
=−−−=−−
∫∫
Получаем интеграл от степенной функции относительно
cos.
x
В случае
1
m
=
сразу имеем:
sincoscos(cos),R.
nn
xxdxxdxn
=−∀∈
∫∫
Аналогично поступают, если в формуле (19.23) n – нечетное
положительное число, т. е. отдельно множитель
cos
x
можно
поднести под знак дифференциала.
2. Если в формуле (19.23)
2,
mnk
+=−
,
k
∈
N
то:
1) подынтегральная функция представляет собой дробь, в
числителе которой находится степень синуса, а в знаменателе –
степень косинуса или наоборот (степень числителя меньше сте-
пени знаменателя), причем показатели степени или оба четные
50
или оба нечетные;
2) подынтегральная функция представляет собой дробь,
числитель которой постоянная величина, а знаменатель – произ-
ведение степеней синуса и косинуса одинаковой четности.
В этих случаях применяют подстановки
tg
tx
=
или
ctg,
tx
=
которые преобразуют подынтегральную функцию в степенную
функцию относительно
tg
x
или
ctg.
x
При этом, если применяют подстановку
tg,
tx
=
то исполь-
зуются формулы:
2222
2
tg11
sin; cos;
1tg11tg1
arctg; .
1
xt
xx
xtxt
dt
xtdx
t
====
++++
==
+
(19.24)
Если применяют подстановку
ctg,
tx
=
то используются
формулы:
2222
2
11ctg
sin; cos;
1ctg11ctg1
arcctg; .
1
xt
xx
xtxt
dt
xtdx
t
====
++++
==−
+
(19.25)
Для дроби первого вида, если в числителе находится сте-
пень
sin,
x
то рациональнее применить подстановку
tg,
tx
=
ес-
ли в числителе находится степень
cos,
x
то – подстановку
ctg.
x
В случае, если
2,
mnk
+=−
,
k
∈
N
числа m и n могут быть не
целыми.
3. Если
0
mn
+=
(m, n – целые числа), то подынтегральное
выражение имеет один из видов
sin
cos
m
m
x
x
или
cos
sin
n
n
x
x
и тогда ин-
теграл приводится к виду tg
m
xdx
∫
или
ctg.
n
xdx
∫
Для вычисле-
ния следует применить соответственно подстановки
tg
xt
=
и
2
1
dt
dx
t
=
+
или
ctg,
xt
=
2
,
1
dt
dx
t
=−
+
которые приводят к инте-
гралам
2
1
m
t
dt
t
+
∫
или
2
1
n
t
dt
t+
∫
соответственно. Выполняя деле-
51
ние (в первом случае
m
t
делим на
2
1,
t
+
а во втором
n
t
– на
2
1
t
+
), придем к выражению, которое непосредственно интегри-
руется.
Для вычисления интегралов вида tg
m
xdx
∫
и
ctg,
m
xdx
∫
,
m
∈
N
можно использовать также формулы:
2
2
1
tg1,
cos
x
x
=−
2
2
1
ctg1,
sin
x
x
=−
(19.26)
последовательно понижая степень тангенса или котангенса.
С помощью формул (19.26) можно вычислять интегралы вида
2
1
tg,
cos
m
n
xdx
x
∫
2
1
ctg,
sin
m
n
xdx
x
∫
где n – целое положительное число, и интегралы вида
2
,
sin
n
dx
x
∫
2
,
cos
m
dx
x
∫
где m, n – целые положительные числа.
4. Интегралы вида
2
sin
n
xdx
∫
и
2
cos,
n
xdx
∫
n
∈
N
вычис-
ляются с помощью тригонометрических формул понижения сте-
пени:
( )
2
2
1
sin(1cos2),
2
1
cos1cos2.
2
xx
xx
=−
=+
(19.27)
Интеграл вида
22
sincos,
mn
xxdx
∫
(19.28)
где
,,
mn
∈
N
вычисляется с помощью формул (19.27) и
формулы
sin22sincos
xxx
=
(19.29)
5. Интеграл вида
(sin,cos),
Rxxdx
∫
где R – рациональная
функция, аргументами которой являются
sin
x
и
cos,
x
т. е. над
синусом и косинусом проводятся только рациональные опера-
ции (сложение и вычитание, умножение на постоянные величи-
ны, возведение в целые степени как положительные, так и отри-
52
цательные, деление), вычисляется с помощью универсальной
тригонометрической подстановки
tg.
2
x
t = При этом
2
2
22
22
2
22
22
2tg1tg
21
sin; cos;
11
1tg1tg
2
2arctg; .
1
xx
xx
tt
xx
tt
dt
xtdx
t
−
−
====
++
++
==
+
(19.30)
Таким способом удобно вычислять интегралы вида
21
,
sin
n
dx
x
+
∫
21
,
cos
n
dx
x
+
∫
а также
,
sincos
dx
axbxc
++
∫
где числа a,
b одновременно не равны нулю.
Вместе с тем, универсальная подстановка
tg
2
x
t = часто при-
водит к громоздким вычислениям, поэтому ее следует применять
в тех случаях, когда невозможно найти более удобный способ.
Частные подстановки
1. Если
(sin,cos)
Rxx
– нечетная функция относительно
sin,
x
т. е.
(sin,cos)(sin,cos),
RxxRxx
−=−
то подынтегральное
выражение приводится к рациональной функции подстановкой
cos.
tx
=
2. Если
(sin,cos)
Rxx
– нечетная функция относительно
cos,
x
т. е.
(sin,cos)(sin,cos),
RxxRxx
−=−
то подынтегральное
выражение приводится к рациональной функции подстановкой
sin.
tx
=
3. Если
(sin,cos)
Rxx
– четная функция относительно
sin
x
и
cos,
x
т. е.
(sin,cos)(sin,cos),
RxxRxx
−−=
то подынтеграль-
ное выражение приводится к рациональной функции подстанов-
кой
tg.
tx
=
4. Интеграл
( )
tg
Rxdx
∫
приводится к рациональной функ-
ции с помощью подстановки
tg.
tx
=
5. Интеграл
(ctg)
Rxdx
∫
приводится к рациональной функ-
ции с помощью подстановки
ctg.
tx
=
53
Пример 1. Найти неопределенный интеграл:
1)
sin2cos4;
xxdx
∫
2)
sin4cos2.
xxdx
∫
Решение. 1) Заменяя произведение
sin2cos4
xx
по формуле
(19.22), получаем:
11
(sin(2)sin6)(sin6sin2)
22
xxdxxxdx
−+=−=
∫∫
11111
cos6cos2cos2cos6.
262412
xxCxxC
=−++=−+
2) Интеграл sin4cos2
xxdx
∫
также можно вычислить, преобразуя
произведение тригонометрических функций в сумму. Используем иной
способ:
( )
2
223
sin4cos22sin2cos2cos22cos2sin2
1
cos22sin2cos2(cos2)cos2.
3
xxdxxxxdxxxdx
xxdxxdxxC
===
=−−==+
∫∫∫
∫∫
Пример 2. Найти неопределенный интеграл:
1)
5
sin2;
xdx
∫
2)
43
sincos;
xxdx
∫
3)
3
6
3
3
cos
.
sin
x
x
dx
∫
Решение. 1) Показатель степени синуса – нечетное натуральное число.
Поэтому в подынтегральной функции выделим первую степень синуса:
542222
sin2sin2sin2sin2(sin2)sin2(1cos2)
xxxxxxx
=⋅==−=
24
sin2(12cos2cos2).
xxx
=−+
Получаем:
524
sin2(12cos2cos2)sin2
xdxxxxdx
=−+=
∫∫
24
1
(12cos2cos2)(2sin2)
2
xxxdx
=−−+−=
∫
( )
( )
24
1
12cos2cos2cos2.
2
xxdx
=−−+
∫
Интегрируя как степенную функцию относительно
cos2,
x
получаем:
35
5
12cos2cos2
sin2cos2
235
xx
xdxxC
=−−++=
∫
54
35
cos2cos2cos2
.
2310
xxx
C
=−+−+
2) В подынтегральной функции выделим степень косинуса:
434242
sincossincoscossin(1sin)cos
xxxxxxxx
==−=
46
(sinsin)cos.
xxx
=−
Получим:
( )
434646
sincos(sinsin)cos(sinsin)sin.
xxdxxxxdxxxdx
=−=−
∫∫∫
Интегрируя как степенную функцию относительно
sin,
x
получаем:
57
43
sinsin
sincos.
57
xx
xxdxC
=−+
∫
3) Поскольку
322
coscoscos1sincos,
33333
xxxxx
=⋅=−
то имеем:
22
3
666
2
6
1
33333
3
333
3
3
1sincos1sincos
cos
3
sinsinsin
1sin
3sin.
3
sin
xxxx
x
xxx
x
x
dxdxdx
x
d
−−
===
−
=
∫∫∫
∫
Применим подстановку
sin.
3
x
t
=
( )
253
64
653
131
333.
53
5
ttt
dtttdtCC
ttt
−−
−−
−
=−=−+=−++
−−
∫∫
Возвращаемся к старой переменной. Заменяем t на
sin
3
x
и полу-
чаем:
3
653
3
333
cos
31
.
sin5sinsin
x
xxx
dxC
=−++
∫
Пример 3. Найти неопределенный интеграл:
1)
4
6
sin
;
cos
x
dx
x
∫
2)
3
7
cos3
;
sin3
x
dx
x
∫
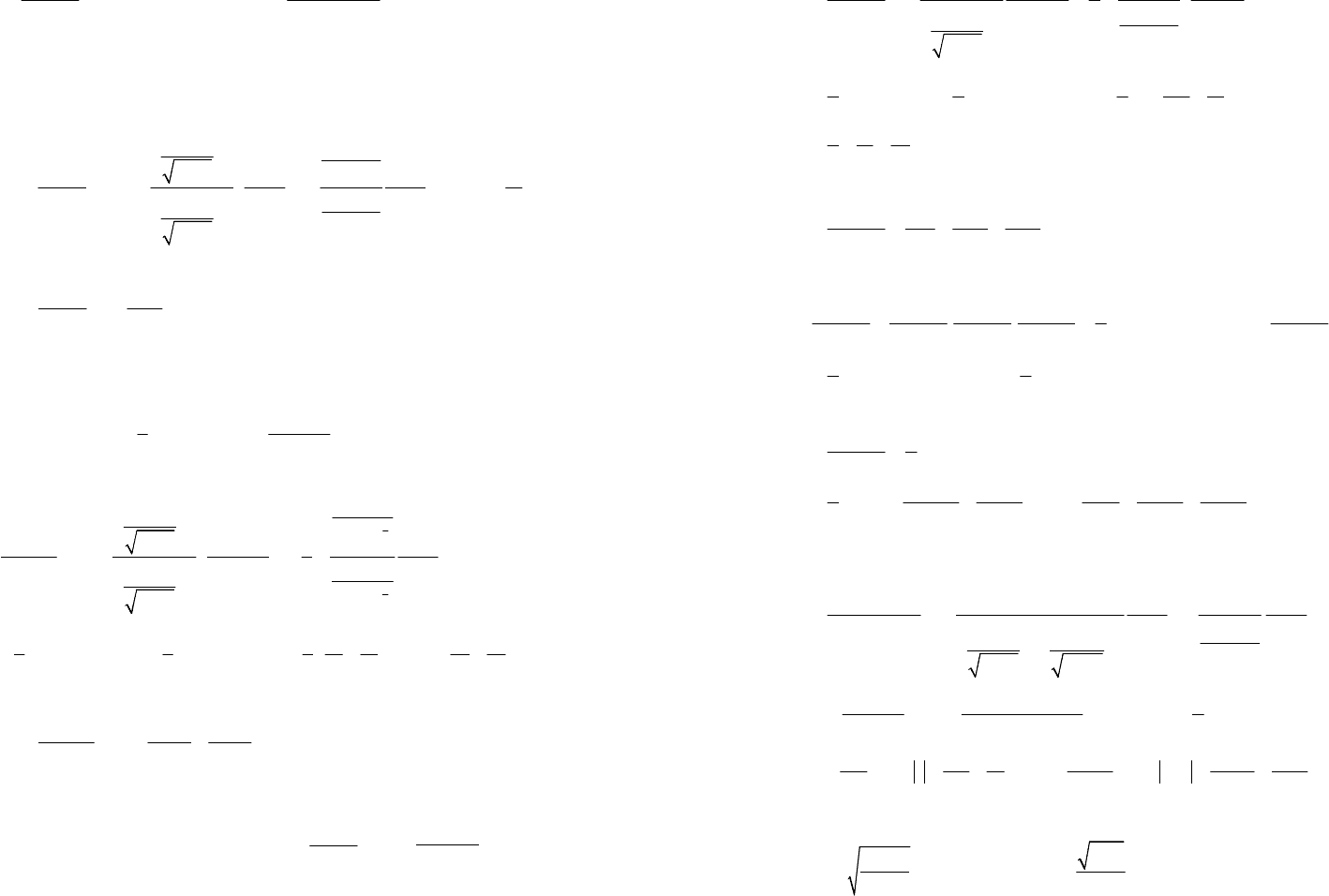
55
3)
6
;
cos2
dx
x
∫
4)
35
.
sincos
dx
xx
∫
Решение. 1) Показатель степени синуса
4,
m
=
показатель степени
косинуса
6,
n
=−
2
mn
+=−
– четное отрицательное число. Так как в
числителе находится степень синуса, то применим подстановку
tg
tx
=
и используем формулы (19.24). Получаем:
4
4
45
22
2
4
6622
23
2
(1)
1
1
1
(1)
1
sin
.
5
cos11
t
t
t
t
t
t
xdtdtt
dxtdtC
xtt
+
+
+
+
====+
++
∫∫∫∫
Заменив t на
tg,
x
окончательно получаем:
45
6
sintg
.
5
cos
xx
dxC
x
=+
∫
2) Показатель степени синуса
7,
m
=−
показатель степени косину-
са
3,
n
=
4
mn
+=−
– четное отрицательное число. Так как в числи-
теле находится степень косинуса, то удобнее применить подстановку
ctg3,
tx
=
2
1
arcctg,.
3
3(1)
dt
xtdx
t
==−
+
Используя формулы (19.25), получаем:
3
2
7
2
3
3
3
2
2
7722
2
2
(1)
1
1
1
1
(1)
cos31
3
sin33(1)1
t
t
t
t
t
t
xdtdt
dx
xtt
+
+
+
+
==−=
++
∫∫∫
()()
4646
3235
111
1.
333461218
tttt
ttdtttdtCC
=−+=−+=−++=−−+
∫∫
Заменив t на
ctg,
x
получаем:
346
7
cos3ctgctg
.
1218
sin3
xxx
dxC
x
=−−+
∫
3) 1-й способ. Показатель степени синуса
0,
m
=
показатель сте-
пени косинуса
6,
n
=−
6
mn
+=−
– четное отрицательное число. При-
меним подстановку
tg2,
tx
=
тогда
arctg
,
2
t
x =
2
.
2(1)
dt
dx
t
=
+
Исполь-
зуя формулы (19.24), получаем:
56
6622
23
2
1
1
(1)
1
111
2
cos22(1)(1)
t
t
dxdtdt
xtt
+
+
===
++
∫∫∫
()
35
2224
35
1112
(1)12
22235
.
2310
tt
tdtttdttC
ttt
C
=+=++=+++=
=+++
∫∫
Заменяем t на
tg
x
и получаем:
35
6
tgtgtg
.
2310
cos2
dxxxx
C
x
=+++
∫
2-й способ. Преобразуем подынтегральное выражение и применим
формулы (19.26):
22
62222
111(2)
(1tg2)(1tg2)
2
cos2cos2cos2cos2cos2
dxdxdx
xx
xxxxx
==++=
( )
( )
( )
( )
2
224
11
1tg2tg212tg2tg2tg2.
22
xdxxxdx
=+=++
Интегрируя как степенную функцию относительно
tg2,
x
получаем:
( )
24
6
3535
1
(12tg2tg2)tg2
2
cos2
12tg2tg2tg2tg2tg2
tg2.
2352310
dx
xxdx
x
xxxxx
xCC
=++=
=+++=+++
∫∫
4) Имеем
5,
m
=−
3,
n
=−
8
mn
+=−
– четное отрицательное чис-
ло. Применим подстановку
tg
tx
=
и формулы (19.24), получаем:
353232
5
24
22
(1)
1
11
sincos11
1
1
t
t
t
t
dxdtdt
xxtt
t
+
+
===
++
+
∫∫∫
23246
33
33
(1)1332
3
tttt
dtdttttdt
t
tt
−
++++
===+++=
∫∫∫
2424
22
1313tgtg
2ln2lntg.
2424
22tg
ttxx
tCxC
tx
=−++++=−++++
Пример 4. Найти неопределенный интеграл:
1)
3
7
sin
;
cos
x
dx
x
∫
2)
5
4
tg
.
cos
x
dx
x
∫
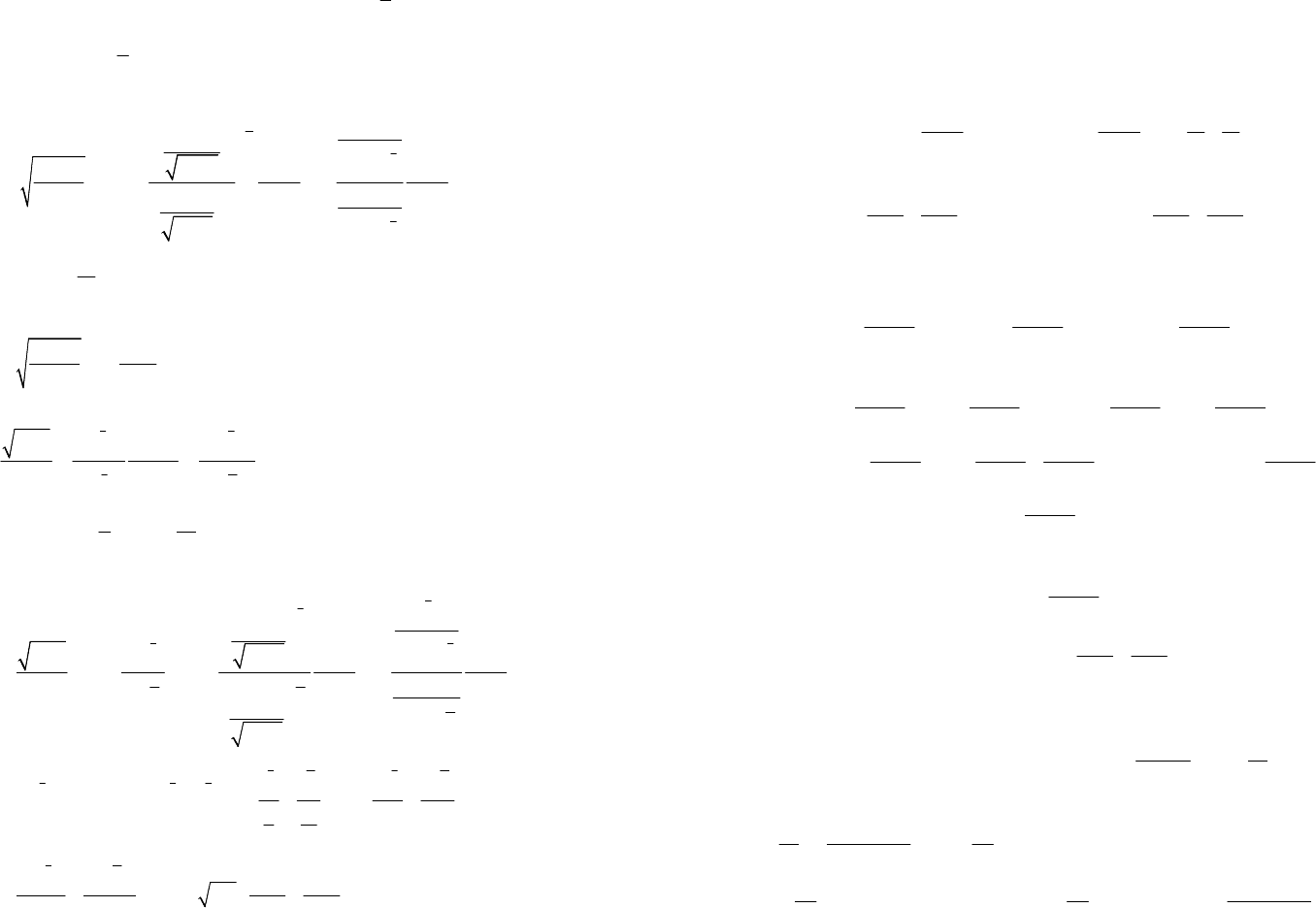
57
Решение. 1) Показатель степени синуса
1
,
3
m
=
показатель степе-
ни косинуса
7
,
3
n
=−
2
mn
+=−
– четное отрицательное число. При-
менив подстановку
tg
tx
=
и формулы (19.24), получаем:
1
6
7
6
1
3
2
2
3
7722
2
2
2
(1)
1
1
1
(1)
sin
1
cos11
.
2
t
t
t
t
t
xdtdt
t
dx
xtt
t
tdtC
+
+
+
+
===
++
==+
∫∫∫
∫
Возвращаемся к старой переменной. Заменяя t на
tg,
x
получаем:
2
3
7
sintg
.
2
cos
xx
dxC
x
=+
∫
2) Преобразуем подынтегральную функцию к виду
55
22
513
22
5
44
tg
sin1sin
.
coscos
coscos
x
xx
xx
xx
==
Имеем
5
,
2
m =
13
,
2
n =−
4
mn
+=−
– четное отрицательное чис-
ло. Применив подстановку
tg
tx
=
и формулы (19.24), получаем:
5
5
2
2
5
5
2
4
1313
22
13
4
5
2
2
422
2
2
(1)
1
1
1
(1)
1
tg
sin
cos11
cos
t
t
t
t
t
t
x
dtdt
dxdx
xtt
+
+
+
+
====
++
∫∫∫∫
(
)
711711
559
2222
222
2
711
22
22
(1)
711
tttt
ttdtttdtCC
=+=+=++=++=
∫∫
711
22
35
2tg2tgtgtg
2tg.
711711
xxxx
CxC
=++=++
58
Пример 5. Найти неопределенный интеграл:
1)
6
tg;
xdx
∫
2)
44
sin5cos5.
xxdx
∫
Решение. 1) 1-й способ. Применяя подстановку
tg
tx
=
и форму-
лы (19.24), получаем:
653
642
22
1
tg1arctg.
53
11
tdttt
xdxttdtttC
tt
==−+−=−+−+
++
∫∫∫
Заменяем t на tg x:
( )
5353
6
tgtgtgtg
tgtgarctgtgtg.
5353
xxxx
xdxxxCxxC
=−+−+=−+−+
∫
2-й способ. Представив подынтегральную функцию в виде
642
tgtgtg
xxx
=⋅ и применив формулу (19.26), получаем:
444422
222
111
tg1tgtgtgtgtg.
coscoscos
xxxxxx
xxx
−=⋅−=⋅−⋅
Еще два раза применим формулу (19.26):
42422
2222
1111
tgtg1tgtgtg
coscoscoscos
xxxxx
xxxx
−−=−+=
( )
4242
2222
1111
tgtg1tgtg11.
coscoscoscos
xxxx
xxxx
=−+−=−+−
Учитывая, что
( )
2
tg,
cos
dx
dx
x
= получим интеграл от рациональ-
ной функции относительно
tg
x
( )
642
2
tgtgtg1
cos
dx
xdxxxdx
x
=−+−=
∫∫∫
( )
( )
53
42
tgtg
tgtg1tgtg.
53
xx
xxdxxxxC
=−+−=−+−+
∫
2) Имеем интеграл вида (19.23). Используя формулу (19.29), полу-
чаем:
4
4444
sin101
sin5cos5(sin5cos5)sin10.
216
x
xxdxxxdxdxxdx
===
∫∫∫∫
Далее, понижая степень по формуле (19.27), имеем:
( )
2
2
11cos201
1cos20
16264
x
dxxdx
−
=−=
∫∫
( )
2
111cos40
12cos20cos2012cos20
64642
x
xxdxxdx
+
=−+=−+=
∫∫
