Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.

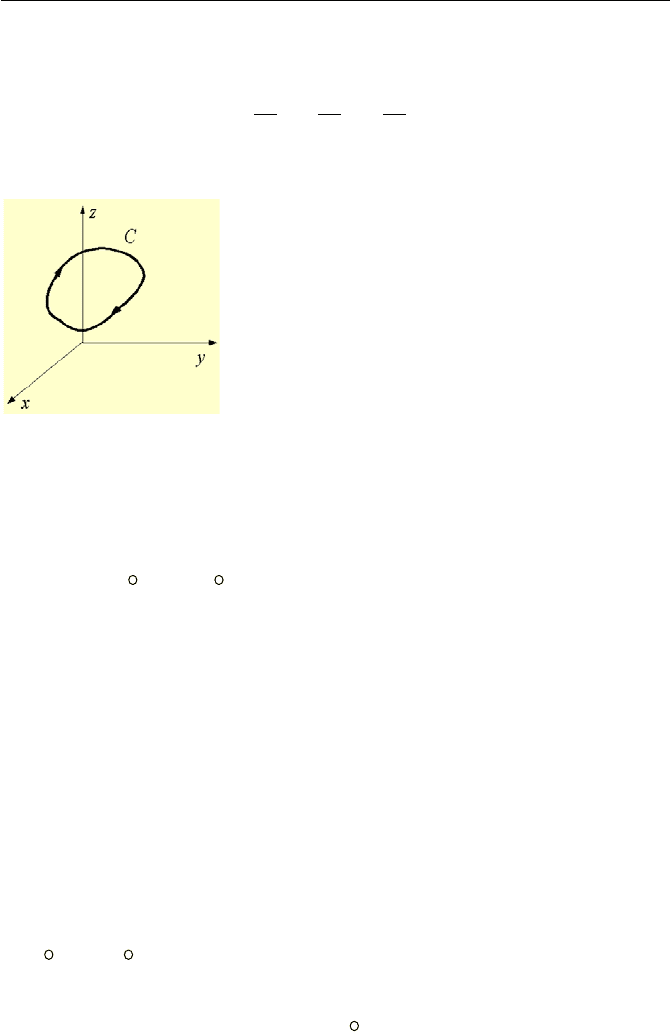
1. Defintion of Terms 953
argument of the integral to be an exact differential (see definition given in Sec-
tion 1), which upon integration would depend only on the end points.
³³³
−==
µ
¶
´
∂
∂
+
∂
∂
+
∂
∂
=∇=⋅
2
1
2
1
)()()(.
12
P
P
C
P
P
C
PfPfdfdz
z
f
dy
y
f
dx
x
f
rdfrdA
K
K
K
K
Figure VIIc.1.7. Line integral along a closed path or loop
If this differential is integrated along a loop, as shown in Figure VIIc.1.7, the line
integral becomes zero:
µ
¶
´
==⋅∇=⋅
³³
C
C
dfrdfrdA 0
K
K
K
K
where the circle on the integral symbol emphasizes closed path integration. For
example, if we want to find the integral of
kzxyjxyzizyA
K
K
K
K
22332
32 ++= along
a segment from points P
1
(0, 0, 0) to P
2
(1, 1, 1), we need not to be concerned about
the function that represents the segment, as the given vector is the gradient of the
potential function f = xy
2
z
3
. Therefore:
[]
1)(32
2
1
2
1
2
1
323222332
===++=⋅
³³³
P
P
P
P
P
PC
zxyzxyddzzxydyxyzdxzyrdA
K
K
The integration of an exact differential depends only on the end points and is in-
dependent of the path. We may also try to find the result of the integration along a
closed path:
[]
0)(32
1
1
1
1
323222332
===++=⋅
³³³
P
P
P
P
CC
zxyzxyddzzxydyxyzdxzyrdA
K
K
Hence we conclude that if 0=×∇ A
K
K
then
0=⋅
³
C
rdA
K
K
.
954 VIIc. Engineering Mathematics: Vector Algebra
Potential energy and conservative force. These terms are applied in the spe-
cial case where the value of the line integral is independent of the path. In this
case, if vector
A
K
represents force, then the function f is known as the potential of
A
K
. Additionally, –f is called the potential energy associated with force
A
K
and
the force itself is said to be conservative.
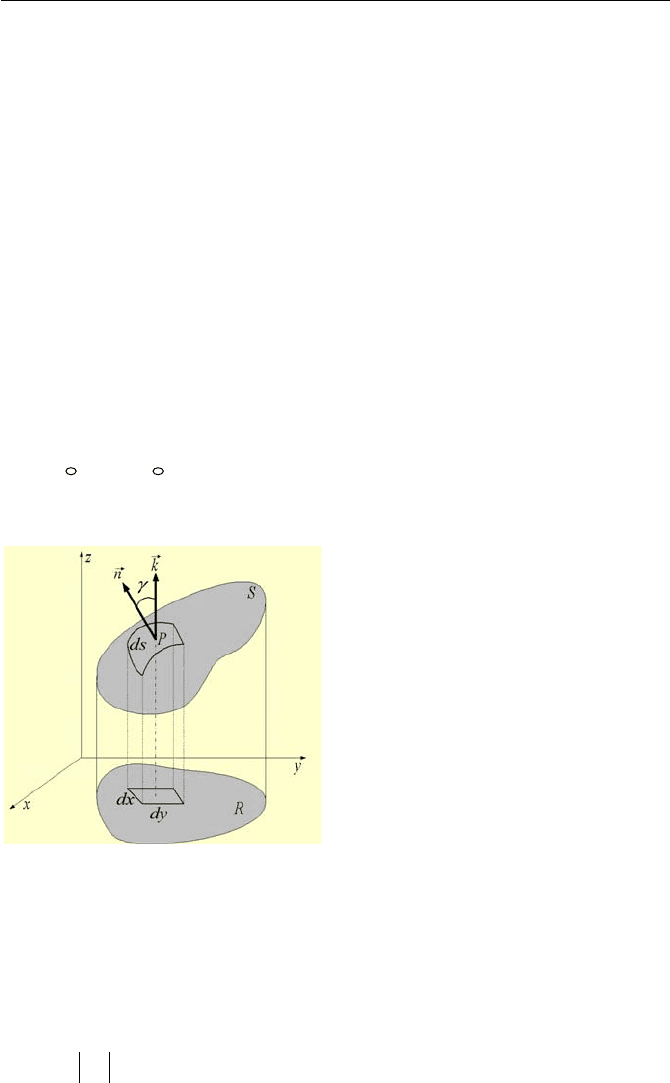
Definition of surface and volume integrals. Integral of vector
A
K
over sur-
face S is defined as the summation of the dot products of
A
K
and the normal vector
n
K
representing an elemental area ds. If the elemental area is sufficiently small,
then the summation becomes:
³³³³
⋅=⋅=
SS
dsnAsdAI
K
K
K
K
VIIc.1.20
where
n
K
is the unit vector normal to the elemental surface ds of surface S, as
shown in Figure VIIc.1.8. Similar definition applies to a volume integral. If sur-
face S is a closed surface (i.e., contains a volume), then the surface integral is writ-
ten as:
³³
⋅=
³³
⋅=
SS
dsnAsdAI
K
K
K
K
VIIc.1.20-1
Figure VIIc.1.8. Depiction of surface and the normal vector
To find an alternative way to express Equation VIIc.1.20-1, we seek to express
the unit vector normal to the surface in terms of the function representing the sur-
face. To do this, you may recall that the gradient of function w = f(x, y, z) is nor-
mal to the surface described by w. We may then express the gradient vector in
terms of the unit vector of the surface:
nww
K
K
K
∇=∇
1. Defintion of Terms 955
Since kzwjywixww
K
K
K
K
)/()/()/( ∂∂+∂∂+∂∂=∇ and
222
)/()/()/( zwzwzw ∂∂+∂∂+∂∂=∇
K
then
222
)/()/()/(
///
zwywxw
kzwjywixw
n
∂∂+∂∂+∂∂
∂∂+∂∂+∂∂
=
K
K
K
K
VIIc.1.21
If the surface is closed (i.e. for surfaces that contain a volume), vector
n
K
tradi-
tionally points outward. We now find projection of the elemental surface ds on
the xy-plane. Since
ds = dxdycos
γ
and the fact that the unit vector k
K
is perpendicular to the xy-plane, we alterna-
tively write this as:
dxdydskn =⋅
K
K
On the other hand, the dot product of two unit vectors is equal to the cosine of the
angle between, hence:
222
)/()/()/(
/
cos
zwywxw
zw
kn
∂∂+∂∂+∂∂
∂∂
±=⋅=
K
K
γ
VIIc.1.22
Putting all these together, we can alternatively write the surface integral (Equa-
tion VIIc.1.20-1) as:
dxdynAdsnAsdAI
SSS
γ
cos
1
³³³³³³
⋅=⋅=⋅=
K
K
K
K
K
K
VIIc.1.23
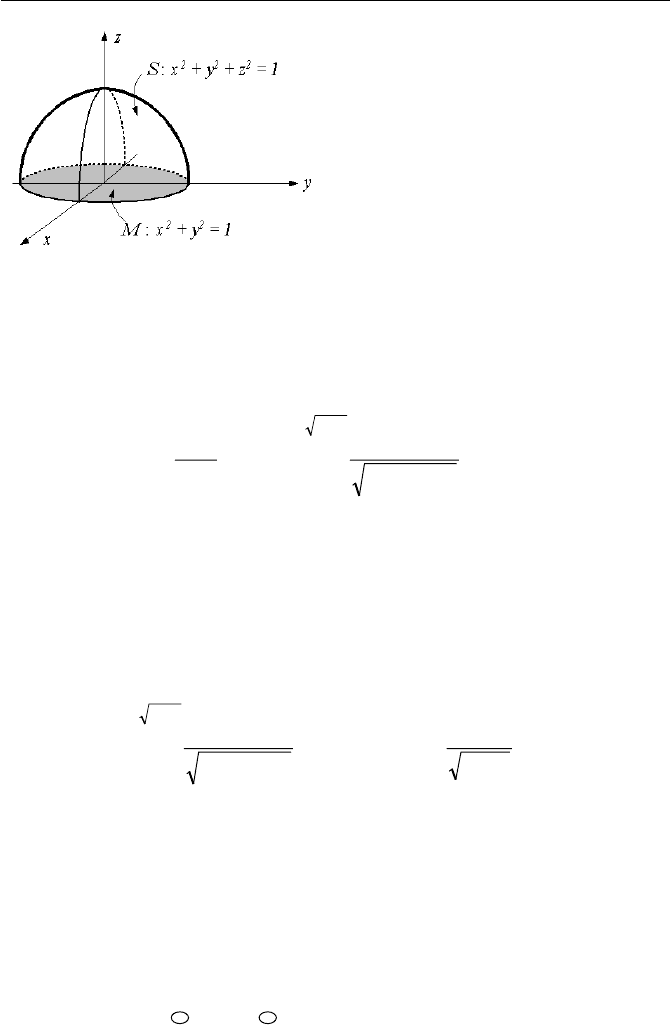
For example, suppose we want to find the surface integral of vector
jyixA
K
K
K
22 +=
over the hemisphere shown in Figure VIIc.1.9. For this purpose, we first deter-
mine the unit vector normal to the surface. The surface function is w = x
2
+ y
2
+ z
2
– 1. The components of the unit vector then become 2x, 2y, and 2z. The absolute
value of the unit vector is 2. Therefore, the unit vector of the hemisphere is:
kzjyixn
K
K
K
K
++=
Cosine of the angle between the unit vector normal to the surface and the unit vec-
tor normal to the xy-plane from Equation VIIc.1.22 becomes
z
=
γ
cos . There-
fore, from Equation VIIc.1.23, we have:
³³³³³³
+=++⋅+=⋅=
TSS
z
dxdy
yx
z
dxdy
kzjyixjyixdxdynAI )(2)()22(
cos
1
22
K
K
K
K
K
K
K
γ
956 VIIc. Engineering Mathematics: Vector Algebra
Figure VIIc.1.9. Hemisphere for calculation of a surface integral
Where the surface integral is now developed on the circle M which is the projec-
tion of the hemisphere. Replacing z from the function representing the hemi-
sphere surface,
³³
µ
µ
µ
¶
´
µ
µ
¶
´
−−
+
=+=
=
−
=
T
x
x
y
dxdy
yx
yx
z
dxdy
yxI
1
0
1
0
22
22
22
2
1
)(2
4)(2
Note that the limits of the double integral span only one quarter of the circle in the
xy-plane (i.e. in the +x and +y region). Due to symmetry we multiplied the inte-
gral by 4 to cover the entire surface of the circle. We practically solved the bulk of
the problem. The rest deals with carrying out this integral. Generally, it is easier
to carry out double integrals in a polar coordinate. Recall that in polar coordi-
nates,
θ
cosrx = and
θ
sinry = . Therefore, x
2
+ y
2
= r
2
and
θ
rdrddxdy =
.
Therefore, the integral becomes:
3/8
1
8
1
)(
8
2/
0
1
0
2
2
1
0
1
0
22
22
2
πθ
π
θ
=
µ
µ
¶
´
µ
µ
¶
´
−
=
µ
µ
µ
¶
´
µ
µ
¶
´
−−
+
=
=
=
=
−
=
r
x
x
y
rdrd
r
r
dxdy
yx
yx
I
Carrying out surface integrals is generally not a straightforward integration. This
can be easily verified by trying to integrate
kzjyixA
K
K
K
K
++= over the same hemi-
sphere surface instead of the vector used in the above example. The difficulty of
integration over surfaces is remedied by Gauss’s divergence theorem.
Gauss divergence theorem relates an integral over a closed surface to an inte-
gral in the volume enclosed by the surface. For example, if volume V is enclosed
by surface S, then:
³³³³³³³
⋅=⋅=⋅∇
SS
dsnAsdAdA
K
K
K
K
K
V)(
V

1. Defintion of Terms 957
An intuitive case is when volume V is a sphere and
A
K
represents density of an in-
compressible fluid multiplied by the flow velocity (mass flux). In this case, the
rate of change of mass inside the sphere is due to the flow of the incompressible
liquid across the surface of the sphere.
We now try to solve the previous example of integration over the surface of a
hemisphere. To obtain a closed surface, we use the circle obtained from the inter-
section of the xy-plane with the hemisphere to contain the volume. We note that
the integral of the given vector over this surface is zero because the given vector
has no component in the z-direction. Therefore, the integral over the surface of
the hemisphere is equal to the divergence of the given vector in the volume of the
hemisphere. The divergence of the given vector is
4=⋅∇ A
K
K
. Therefore:
3/8)3/2(4V4V)(
VV
ππ
===⋅∇=⋅
³³³³³³³³
ddAdsnA
S
K
K
K
As an exercise, the reader may develop the surface integral of kzjyixA
K
K
K
K
++=
over the hemisphere of Figure VIIc.1.8.
Stokes curl theorem is the two dimensional form of the Gauss’s theorem. It
expresses that the circulation of a vector around a closed curve C is equal to the
flux of the vector over S, the area enclosed by C:
dsnASdArdA
SS
C
K
K
K
K
K
K
K
K
⋅×∇=⋅×∇=⋅
³³³³³
)()( VIIc.1.24
where
rd
K
is an elemental vector in the direction of integration along curve C and
n
K
is the unit vector normal to the elemental area ds. Directions of these two vec-
tors are as follows: if unit vector
rd
K
moves counterclockwise around the horizon-
tal curve C (right-hand screw), the direction of unit vector
n
K
is upward, if the
elemental vector
rd
K
moves clockwise around the horizontal curve C (right-hand
screw), the direction of unit vector
n
K
is downward. For example, let us verify the
Stokes curl theorem for the paraboloid of Figure VIIc.1.10. The function repre-
senting the surface is given by z = 1 – x
2
– y
2
and the function representing the in-
tersection with the xy plane is given by x
2
+ y
2
= 1. These are surfaces S and M in
Figure VIIc.1.10, respectively.
z
y
x
z = 1 - x
2
- y
2
C
S
R=1
M
Figure VIIc.1.10. Depiction of a circular paraboloid

958 VIIc. Engineering Mathematics: Vector Algebra
The goal is to first develop the line integral of the vector:
kyxjxziyzA
K
K
K
K
)()()( +−++−=
along the closed path C,
³
⋅=
C
rdAI
K
K
1
. Then to carry out
³³
⋅×∇=
S
dsnAI
K
K
K
2
and
to show that I
1
= I
2
. To develop the line integral:
³³
+−++−=++⋅+−++−=
CC
dzyxdyxzdxyzkdzjdyidxkyxjxziyzI ])()()[(][])()()[(
1
K
K
K
K
K
K
we first note that the integration is along path C, which is in the xy plane. As a re-
sult, I
1
simplifies to:
³
+−
³
=+−++−=
CC
xdyydxdzyxdyxzdxyzI ][])()()[(
1
To simplify integration, we take advantage of the polar coordinates. This is true,
as in this case, r remains constant (r = R = 1). Hence, we are replacing both x and
y with a single variable
θ
. To do this, recall that
θ
cosrx = and
θ
sinry = . Set-
ting r = 1 and substituting x and y into I
1
we get:
πθθθθθθθ
π
θ
π
θ
2)])(cos(cos)sin)((sin[][
2
0
2
0
1
=
³³
=+−−=
³
+−=
==
dddxdyydxI
C
Let’s now try the surface integral. For this purpose, we must first find the curl of
the given vector:
)(2 kji
yxxzyz
zyx
kji
A
K
KK
K
K
K
K
K
++−=
−−+−
∂
∂
∂
∂
∂
∂
=×∇
Next, we need to find the unit vector normal to surface S and the cosine of the an-
gle between the unit vectors normal to the surfaces S and M. The unit vector nor-
mal to S is given by Equation VIIc.1.21 where w for a positive unit vector normal
to the surface of the paraboloid is w = z + x
2
+ y
2
– 1:
[
]
mn
ij
aA =
Therefore;
1)(4
244
1)(4
22
)(2
2222
++
++−
=
++
++
⋅++−=⋅×∇
yx
yx
yx
kjyix
kjinA
K
K
K
K
K
K
K
K
K
Finally the cosine of the angle between the unit vector normal to S and the unit
vector normal to M is given by Equation VIIc.1.22 as:

1. Defintion of Terms 959
6
1)(4
1
)/()/()/(
/
cos
22222
++
=
∂∂+∂∂+∂∂
∂∂
=
yxzwywxw
zw
γ
We now can find I
2
as:
³³³³
⋅×∇=⋅×∇=
SS
dxdy
nAdsnAI
γ
cos
2
K
K
K
K
K
K
Substituting for the dot product of the cosine, I
2
becomes:
³³³³³³ ³³
++−=++−=
MM
M
M
dxdyydxdyxdxdydxdyyxI 244)244(
2
where the first two integrals on the right-hand side cancel out. Hence, I
2
finally
becomes:
πθ
π
θ
22
2
0
1
0
2
³³
==
== drdrI
r
The Stokes curl theorem is useful in finding an alternative to complicated line in-
tegrals. This is because, in the Gauss divergence theorem and the Stokes curl
theorem, the derivative of the vector is taken, which reduces the degree of the in-
volved terms.
Green’s theorem. Consider
1
ϕ
and
2
ϕ
as two scalar functions of position.
Green’s theorem states:
()
³³³³³
⋅∇=∇⋅∇−∇
S
dsnd
K
K
K
K
21
V
212
2
1
V
ϕϕϕϕϕϕ
Green’s theorem can alternatively be written as:
()
()
³³³³³
⋅∇−∇=∇−∇
S
dsnd
K
1221
V
1
2
22
2
1
V
ϕϕϕϕϕϕϕϕ
where surface S contains volume V. There are two special cases to this theorem.
In the first case, the two scalar functions are equal. In this special case, Green’s
theorem becomes:
³³³³³³³
∂
∂
=⋅∇=∇−∇
SS
ds
n
dsnd
ϕ
ϕϕϕϕϕϕ
K
V])([
V
22
In the second special case, one function is zero:

960 VIIc. Engineering Mathematics: Vector Algebra
³³³³³
∂
∂
=∇
S
ds
n
d
ϕ
ϕ
V
V
2
VIIc.1.25
Leibnitz formula for differentiating integrals provides a useful means of dif-
ferentiating integrals without the need to carry out integrals if there is no analytic
means of integration. For example, if the derivative of
)(x
ϕ
is needed where
)(x
ϕ
is given as an integral function of f(x),
³
=
)(
)(
),()(
xB
xA
dttxfx
ϕ
then,
)(' x
ϕ
is given as:
³
−+
∂
∂
=
³
)(
)(
)(
)(
),(),(
),(
),(
xB
xA
xB
xA
dx
dA
Axf
dx
dB
Bxfdt
x
txf
dttxf
dx
d
VIIc.1.26
where f(x, t), A(x), and B(x) must be continuously differentiable with respect to x.
Example: Find the derivative of y with respect to x given
³
2
2
)(
x
x
dttxxy =
Solution: Since f(x, t) = tx
2
, A(x) = x, and B(x) = x
2
. Hence, =∂∂ xtxf /),( 2xt,
dB/dx = 2x, and dA/dx = 1. Substituting in Equation VIIc.1.26 yields:
()
()
()
()
()
35352342
232122
2
22
xxxxxtxxxtxdtdttx
dx
d
x
x
x
x
x
x
−=−+=
³
−+=
³
To verify the results we obtained, we may directly integrate the given function and
substitute the limits:
³
()( )
2/2/)(
46222
2
2
xxtxdttxxy
x
x
x
x
−===
Thus, dy(x)/dx = (6x
5
– 4 x
3
)/2 = 3x
5
– 2x
3
, which verifies the results obtained
above. In this example, we could easily carry out the integral with respect to t and
then take the derivative with respect to x. However, the Leibnitz rule is helpful in
cases where the integral can not be easily carried out. For example, see Equa-
tion IVa.9.10.
Leibnitz formula for differentiating a triple integral is a description of the
Lagrangian versus Eulerian viewpoints in describing a flow field, as discussed in
Chapter IIIa. The Leibnitz formula for differentiating a triple integral is an exten-
sion of the Leibnitz formula for differentiation of an integral. This formula states

1. Defintion of Terms 961
that the rate of change of c(x, y, z, t), either a scalar or a vector, in a closed region
V is given by:
³³³ ³³
SdVtrcd
t
trc
dtrc
dt
d
S
S
K
K
K
K
K
⋅
µ
¶
´
µ
¶
´
µ
¶
´
+
∂
∂
=
V
V
),(V
),(
V),( VIIc.1.27
In Equation VIIc.1.27,
S
V
K
represents the velocity of surface S, encompassing
volume V. If Volume V is a deformable volume then
S
V
K
is a function of spatial
coordinate. If volume V is accelerating or decelerating then
S
V
K
is also a function
of time. Thus in general,
S
V
K
= ),( trf
K
. Also ndSSd
K
K
= , where n
K
is the unit
vector of surface S.
Equation VIIc.1.27 is the expression of the general transport theorem. If vol-
ume V contains certain fluid mass encompassed by surface S, the surface velocity
becomes the fluid velocity V (i.e.,
S
V
K
= V
K
), the total derivative (d/dt) is replaced
by the substantial derivative, and Equation VIIc.1.27 is written as:
³³³
³³
µ
¶
´
µ
¶
´
µ
¶
´
⋅+
∂
∂
=
Vm
mVm
V
),(
V),(
S
SdVcd
t
trc
dtrc
Dt
D
K
K
K
K
VIIc.1.28
where Vm stands for the material volume enclosed by Sm. Equation VIIc.1.28 is
now referred to as the Reynolds transport theorem. We may relate the total and
the substantial derivatives by eliminating the volume integral of the partial deriva-
tive to obtain the relation between the control volume and the material volume at
the instant they coincide:
³³³
³³
³³³
V
V
),(V),(V),(
S
r
SdVtrcdtrc
dt
d
dtrc
D
t
D
K
K
KKK
⋅+= VIIc.1.29
where in Equation VIIc.1.29,
sr
VVV
KKK
−= represents the relative velocity of the
fluid in volume V with respect to the velocity of surface S encompassing volume
V. The intensive and extensive properties of a system can be related if we intro-
duce y such that
ρ
/),( trcy
K
= . The integral in the left side can then be replaced
by Y so that y = DY/Dm. Substituting, Equation VIIc.1.29 simplifies to:
³³
³³³
V
V
S
r
SdVydy
dt
d
D
t
DY
K
K
⋅+=
ρρ
VIIc.1.30
Equation VIIc.1.30 applies to a general case of deformable and moving control
volumes. In a specific case that the control volume is fixed (V
s
= 0, V
r
= V), Equa-
tion VIIc.1.30 can be written as:
()
³³
µ
¶
´
µ
¶
´
µ
¶
´
⋅+
∂
∂
=
V
V
S
SdVydy
tDt
DY
K
K
ρρ
=
³³
³³³
V
V
S
SdVydy
t
K
K
⋅+
∂
∂
ρρ
VIIc.1.31

962 VIIc. Engineering Mathematics: Vector Algebra
For example, a control volume representing a pump is a fixed control volume. In
contrast, filling a balloon or draining a tank requires deformable control volumes
to represent the air in the balloon or water in the tank.
Harmonic functions. A harmonic function is the solution to the Laplace dif-
ferential equation VIIa.1.1 that has continuous second-order partial derivative.
