Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.


1. Defintion of Terms 943
VIIc. Vector Algebra
1. Defintion of Terms
Types of physical quantities: There are three types of physical quantities, scalar
(temperature), vector (velocity), and tensor (fluid stress and thermal conductivity).
Scalars are zero order tensors. Vectors are first order tensors. A second order ten-
sor is an array of nine components:
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
©
§
=
zzzyzx
yzyyyx
xzxyxx
τττ
τττ
τττ
τ
In this section, an arbitrary scalar is represented by f, an arbitrary vector is repre-
sented by
A
K
and an arbitrary tensor is represented by
τ
.
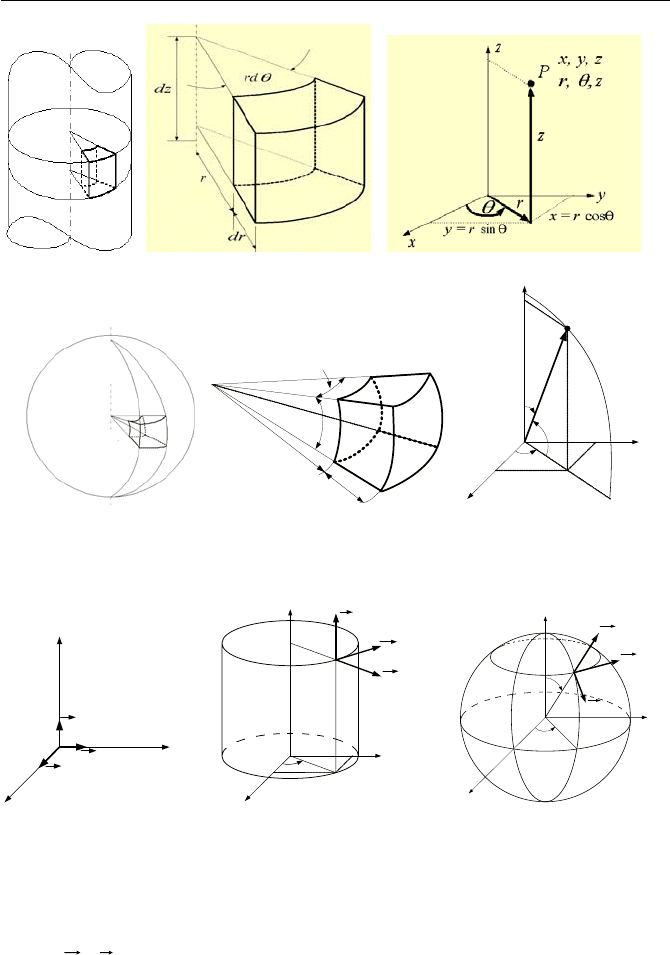
Coordinate systems: There are three Orthogonal systems; Cartesian, cylindri-
cal and spherical coordinates. The Cartesian refers to the rectangular coordinates
for x, y, and z. The circular cylinder refers to r,
θ
, and z and the spherical refers
to r,
θ
, and
φ
. The cylindrical and spherical are examples of curvilinear coordi-
nates. The two-dimensional cylindrical coordinate in the x-y plane is referred to as
the polar coordinate. The elemental area in the Cartesian coordinates is dxdy and
in a polar coordinate is
θ
rdrd .
If earth is treated as a sphere and P is a point on the earth’s surface in the
northern hemisphere, for example, then the latitude of point P is angle
α
= 90
o
–
ϕ
o
. The longitude of point P is
β
= 360
o
–
θ
o
. The semi-circle in the r - z plane is
referred to as the meridian.
Differential volume: The elemental volume in Cartesian coordinates is
dV
Cartesian
= dxdydz, in a cylindrical coordinates is dV
Cylindrical
= rdrd
θ
dz, and in a
spherical coordinates is dV
Spherical
= r
2
sin
φ
d
θ
d
φ
dr.
Unit vector: A vector with the absolute value, magnitude, or length of unity is
a unit vector. Thus the unit vector for vector
A
K
is given by AAu
a
K
K
K
/= . Unit
vectors in the Cartesian coordinate system are traditionally shown by
i
K
, j
K
, and
k
K
. Figure VIIc.1.2 shows the unit vectors in various coordinate systems.
Vector components: A vector, in general, is represented by three components:
332211
uAuAuAA
uuu
KKK
K
++=
where
ui
A is the component along the ith axes having a unit vector
i
u
K
. In the
Cartesian coordinate system for example, the vector is represented as
kAjAiAA
zyx
K
K
K
K
++= where i
K
, j
K
, and k
K
are the unit vectors along x-, y-, and z-
944 VIIc. Engineering Mathematics: Vector Algebra
r
rd
ϕ
dr
(rsin
ϕ)
d
θ
P
x
y
z
r
x, y, z
ϕ
θ
x
=
r
s
i
n
ϕ
c
o
s
θ
y=rsin
ϕ
sin
θ
z=rcos
ϕ
α
z
=
r
s
i
n
ϕ
r,
θ
,
ϕ
Figure VIIc.1.1. Cylindrical and spherical coordinates in the Cartesian coordinate system
x
y
z
i
j
k
x
y
z
θ
k
u
r
r
z
u
θ
x
y
z
u
r
u
θ
u
φ
θ
φ
Figure VIIc.1.2. Unit vectors in Cartesian, cylindrical, and spherical coordinates
axes, respectively. In Figure VIIc.1.3, vector A
K
is represented by the line seg-
ment connecting point P
1
(x
1
, y
1
, z
1
) to point P
2
(x
2
, y
2
, z
2
) so that:
12
rrA −=
K
Substituting for the components comprising vectors r
1
and r
2
we get A
x
= x
2
– x
1
,
A
y
= y
2
– y
1
, and A
z
= z
2
– z
1
.
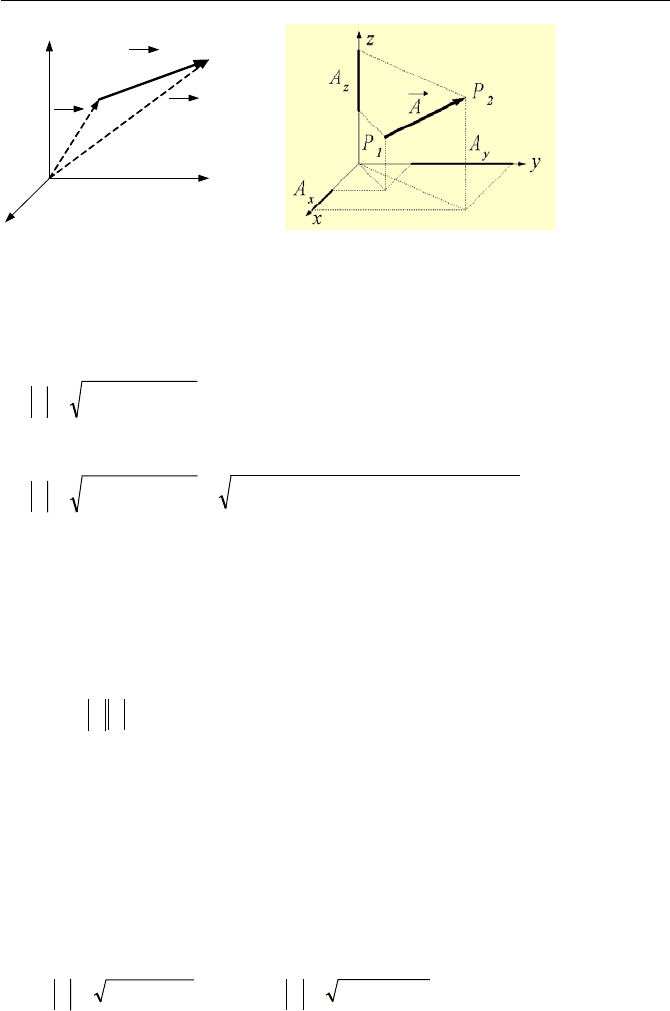
1. Defintion of Terms 945
x
y
z
A
r
2
r
1
P
1
P
2
Figure VIIc.1.3. Depiction of vector A
K
in Cartesian coordinates
Absolute value of a vector written in the Cartesian coordinate system, for ex-
ample, is defined as:
222
zyx
AAAA ++=
K
In case of Vector A
K
shown in Figure VIIc.1.2, the absolute value is given as:
2
12
2
12
2
12
222
)()()( zzyyxxAAAA
zyx
−+−+−=++=
K
Summation of vectors: For vectors A
K
and
B
K
, the summation is defined as:
()
()
()
kBAjBAiBABA
zzyyxx
K
K
K
K
K
+++++=+
Scalar or dot product of two vectors results in a scalar. For vectors
A
K
and
B
K
, dot product is defined as:
ϕ
cosBABA
K
K
K
K
=⋅
Where
ϕ
is the angle between the two vectors. Thus, for two vectors in the Car-
tesian coordinate system, the dot product becomes:
()()
()
()
()
zzyyxxzyxzyx
BABABAkBjBiBkAjAiABA ++=++⋅++=⋅
K
KK
K
KK
K
K
VIIc.1.1
According to this definition,
2
A
A
A
=⋅
K
K
.
Example: To find the angle between vector
kjiA
K
K
K
K
643 −+= and
kjiB
K
K
K
K
115 ++−= , we first find: =−++−=⋅ )11)(6()5)(4()1)(3(BA
K
K
–49. Next
find
416.736163 =++=A
K
, =++= 121251B
K
12.124, and cos(
ϕ
) = –
49/(7.416
× 12.124) = –0.545. Therefore,
ϕ
= 123
o
.
946 VIIc. Engineering Mathematics: Vector Algebra
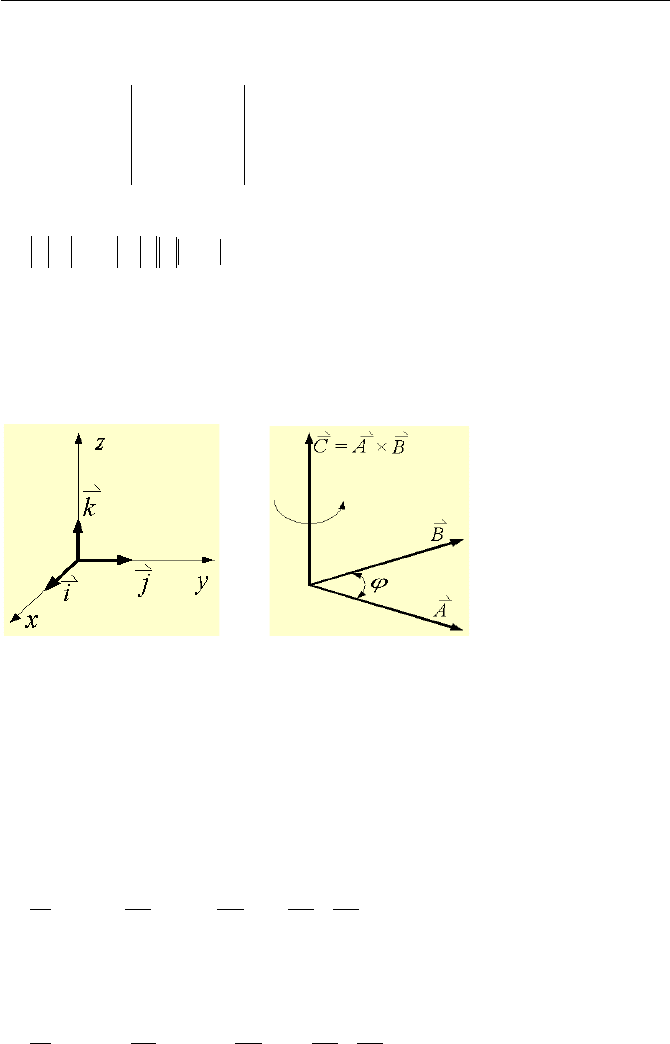
Vector or cross product of two vectors is another vector. The cross product
of two vectors is defined as:
zyx
zyx
BBB
AAA
kji
BAC
K
K
K
K
KK
=×=
VIIc.1.2
The resultant vector has an absolute value of:
ϕ
sinBABAC
K
K
K
K
K
=×=
According to this definition, 0=× AA
K
K
. The resultant vector C
K
is perpendicular
to the plane of vectors
A
K
and
B
K
. The positive direction of vector C
K
follows the
right-hand rule as shown in Figure VIIc.1.4. According to this definition,
A
B
B
A
K
KK
K
×−=×
.
(a) (b)
Figure VIIc.1.4. a) Unit vectors in a Cartesian coordinates. b) Depiction of a cross
product vector
Differentiation of vectors. Since vector operations are not generally linear
operations, care must be exercised in carrying out differentiation of vectors. For
example, the dot product is a linear operation. Hence, the derivative of a dot
product is also a linear operation:
A
dt
Bd
dt
Ad
B
dt
Bd
AB
dt
Ad
BA
dt
d
K
K
K
K
K
K
K
K
K
K
⋅+⋅=⋅+⋅=⋅ )(
On the other hand, the cross product of two vectors is not a linear operation.
Hence, the derivative of the cross product of two vectors is:
A
dt
Bd
dt
Ad
B
dt
Bd
AB
dt
Ad
BA
dt
d
K
K
K
K
K
K
K
K
K
K
×+×≠×+×=× )(
1. Defintion of Terms 947
Linear independence is defined for a set of vectors so that the relation
0=
¦
m
ii
Ac
K
is satisfied only if the following condition exists for the coefficients
0
321
====
m
cccc !
Otherwise, the set of vectors would be linearly dependent.
Plane normal to a vector. Consider a vector given as
kAjAiAA
zyx
K
K
K
K
++= .
The equation of a plane normal to this vector at point P
0
(x
0
, y
0
, z
0
) is given as:
0)()()(
000
=−+−+− zzAyyAxxA
xxx
Independence from coordinate system, Symbol del as a vector operator. It
is very convenient and mathematically elegant to use a symbol for making formu-
lae independent of the coordinate system. Such a symbol is called del (
∇
K
) and
used as a vector operator. For example, in the Cartesian coordinate system, del is
defined as:
k
z
j
y
i
x
K
K
K
K
∂
∂
+
∂
∂
+
∂
∂
=∇
Several uses of the del operator, such as gradient, divergence, and Laplacian are
discussed below.
The Gradient operator (
∇
K
). The gradient operator generally acts on a scalar
and produces a vector. In the Cartesian coordinate system the del operator is writ-
ten as:
k
z
f
j
y
f
i
x
f
f
K
K
K
K
∂
∂
+
∂
∂
+
∂
∂
=∇
VIIc.1.3
In the cylindrical coordinate system as:
zr
u
z
f
u
f
r
u
r
f
f
K
K
K
K
∂
∂
+
∂
∂
+
∂
∂
=∇
θ
θ
1
VIIc.1.4
and in the spherical coordinate system as:
φθ
φθφ
u
f
r
u
f
r
u
r
f
f
r
K
K
K
K
∂
∂
+
∂
∂
+
∂
∂
=∇
1
sin
1
VIIc.1.4
The gradient operator may also operate on a vector to produce a tensor, referred to
as a dyad. For example, in the Cartesian coordinate system:

948 VIIc. Engineering Mathematics: Vector Algebra
¸
¸
¸
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
¨
¨
¨
©
§
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=∇
z
A
y
A
x
A
z
A
y
A
x
A
z
A
y
A
x
A
A
zzz
yyy
x
y
x
K
K
In the discussion below we demonstrate that for f(x, y, z), the gradient of f is in the
direction of the normal to the surface S described by f (Figure VIIc.1.5)
fn
n
f
∇⋅=
∂
∂
K
K
VIIc.1.5
Figure VIIc.1.5. Gradient vector normal to an isothermal or equipotential surface
Consider a function such as w = f(x, y, z). The points at which this function has
the same value, such as w
0
has at a specific point P
0
(x
0
, y
0
, z
0
), in general consti-
tute a surface in space. The equation of this surface is given as f(x, y, z) – w
0
= 0
where w
0
is a constant. In electrical engineering, if w represents the electrical po-
tential, then the surface is called an equipotential surface. In thermal sciences, if
w represents temperature, then the surface is called an isothermal surface. It can
be shown that the gradient vector is normal to these types of surfaces. For exam-
ple, suppose we want to find the plane that is tangent to the surface z = x
2
– y
2
at
point P
0
(2, 1, 3). To find the equation of such a plane we should find the gradient
at point P
0
which, we know is normal to the above surface (i.e., surface z = x
2
–
y
2
). To do this, we first write the equation of the surface as f(x, y, z) = x
2
– y
2
– z =
0 and then find the gradient vector:
kjyixk
z
f
j
y
f
i
x
f
f
K
K
K
K
K
K
K
−−=
∂
∂
+
∂
∂
+
∂
∂
=∇
22
The gradient vector at the specified point is kjikjyixf
K
K
K
K
K
K
K
32422 −−=−−=∇ .
This vector is normal to surface z = x
2
– y
2
at P
0
. The equation of the plane normal
to this vector hence tangent to the surface at P
0
is 4(x – 2) –2(y – 1) – 3(z – 3) = 0
or 3z + 2y – 4x = 1. Later in this section, the application of the gradient operator
in developing surface integrals is discussed.

1. Defintion of Terms 949
The divergence operator ( ⋅∇
K
). Divergence acts on a vector and produces a
scalar. In Cartesian coordinates system, the divergent operator is written as:
z
A
y
A
x
A
A
z
y
x
∂
∂
+
∂
∂
+
∂
∂
=⋅∇
K
K
VIIc.1.6
in the cylindrical coordinate system as:
z
A
A
r
rA
r
r
A
z
r
∂
∂
+
∂
∂
+
∂
∂
=⋅∇
θ
θ
1
)(
1
K
K
VIIc.1.7
and in the spherical coordinate system as:
)sin(
sin
1
sin
1
)(
1
2
2
φ
φφθφ
φ
θ
A
r
A
r
Ar
r
r
A
r
∂
∂
+
∂
∂
+
∂
∂
=⋅∇
K
K
VIIc.1.8
If vector
A
K
happens to be the gradient of a scalar, then the divergence operation
produces Laplacian:
ffA
2
)( ∇=∇⋅∇=⋅∇
K
K
K
K
The Laplacian operator (
2
∇ ). This operator primarily acts on scalars and
produces scalars:
2
2
2
2
2
2
2
z
f
y
f
x
f
f
∂
∂
+
∂
∂
+
∂
∂
=∇
VIIc.1.9
The Laplacian operator in the cylindrical coordinate system is written as:
2
2
2
2
2
2
1
)(
1
z
ff
r
r
f
r
rr
f
∂
∂
+
∂
∂
+
∂
∂
∂
∂
=∇
θ
VIIc.1.10
and in the spherical coordinate system as:
)(sin
sin
1
sin
1
)(
1
22
2
22
2
2
2
φ
φ
φ
φθφ
∂
∂
∂
∂
+
∂
∂
+
∂
∂
∂
∂
=∇
f
r
f
r
r
f
r
r
r
f
VIIc.1.11
Laplacian may also operate on vectors but the vectors must be written in the Car-
tesian coordinate system. The Laplacian of vector
A
K
in the Cartesian coordinate
system is given as:
k
z
A
y
A
x
A
j
z
A
y
A
x
A
i
z
A
y
A
x
A
A
zzz
yyy
xxx
K
KK
K
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
=∇
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
For a vector written in other (i.e. cylindrical and spherical) orthogonal coordinate
systems, the Laplacian can be found from:
950 VIIc. Engineering Mathematics: Vector Algebra
() ( )
AAA
K
K
K
K
K
K
K
×∇×∇−⋅∇∇=∇
2
The Curl operator ( ×∇
K
). This operator acts on vectors and produces vectors.
The curl operator in the Cartesian coordinate system can be obtained from the
definition of the cross products of two vectors:
zyx
AAA
zyx
kji
A
∂
∂
∂
∂
∂
∂
=×∇
K
K
K
K
K
VIIc.1.12
The result is the following vector:
k
y
A
x
A
j
z
A
x
A
i
z
A
y
A
A
x
y
x
z
y
z
K
K
K
K
K
¸
¸
¹
·
¨
¨
©
§
∂
∂
−
∂
∂
+
¸
¹
·
¨
©
§
∂
∂
−
∂
∂
−
¸
¸
¹
·
¨
¨
©
§
∂
∂
−
∂
∂
=×∇
The curl operator in the cylindrical coordinate system is written as:
zr
zr
ArAA
zr
uuru
r
A
θ
θ
θ
∂
∂
∂
∂
∂
∂
=×∇
K
K
K
K
K
1
VIIc.1.13
Finally, the curl operator in the spherical coordinate system is given as:
φθ
φθ
φ
φθ
φ
φ
rAArA
r
ururu
r
A
r
r
sin
sin
sin
1
2
∂
∂
∂
∂
∂
∂
=×∇
K
K
K
K
K
VIIc.1.14
If a vector is the gradient of a potential function, then the curl of such a vector is
always equal to zero,
0)( =∇×∇ f
K
K
. Later in this section, the application of the
curl operator in Stokes’ theorem is discussed.
Classical mechanics Hamiltonian operator in the Cartesian coordinate sys-
tem is defined as:
),,()(
2
1
),,(
222
zyxVppp
m
trp
zyxCM
+++=Η
K
K
where m is mass, p is momentum, and V represents the potential energy of a parti-
cle.

1. Defintion of Terms 951
Quantum mechanics Hamiltonian operator is defined as
)(
2
),,(
2
2
rV
m
trp
QM
K
=
KK
+∇
−
=Η
Some useful relations in vector algebra. The relations listed here are fre-
quently used in vector algebra:
0)( =∇×∇ f
K
K
()
0=×∇⋅∇ A
K
K
K
fAAfAf ∇⋅+⋅∇=⋅∇
K
KK
K
K
K
AfAfAf
K
K
K
K
K
K
×∇+×∇=×∇ )(
() () ( )
AAAAAA
K
K
K
K
K
K
K
K
K
×∇×−⋅∇=∇⋅
2
1
()()
() ( )
)( ABBABAABBA
K
K
K
K
K
K
K
K
K
K
K
K
K
K
⋅∇−⋅∇+∇⋅−∇⋅=××∇
Substantial derivative operator D/Dt. The substantial derivative is a mathe-
matical operator that can operate on both scalars or vectors, provided the vector is
written in the Cartesian coordinate system:
()
t
f
fV
D
t
Df
∂
∂
+∇⋅=
KK
VIIc.1.15
where
V
K
is the flow field velocity vector. We can find the substantial derivative
of vectors written in other orthogonal coordinate systems by using Equation
VIIc.1.15 in conjunction with the above vector relations.
Dyadic product of two vectors is a special form of a second-order tensor:
¸
¸
¸
¹
·
¨
¨
¨
©
§
=
332313
322212
312111
wvwvwv
wvwvwv
wvwvwv
wv
KK
Note that, according to this definition, vwwv
K
K
K
K
≠ .
Line, surface, and volume integrals. Integration of vectors along lines and
over surfaces and volumes are used to explain various physical phenomena. For
example, the Stokes theorem as used in flow as well as electrical fields relates line
integrals along a closed path to the surface integral enclosed by the path. The di-
vergence or Gauss theorem relates a volume integral to the surface integral enclos-
ing the volume.
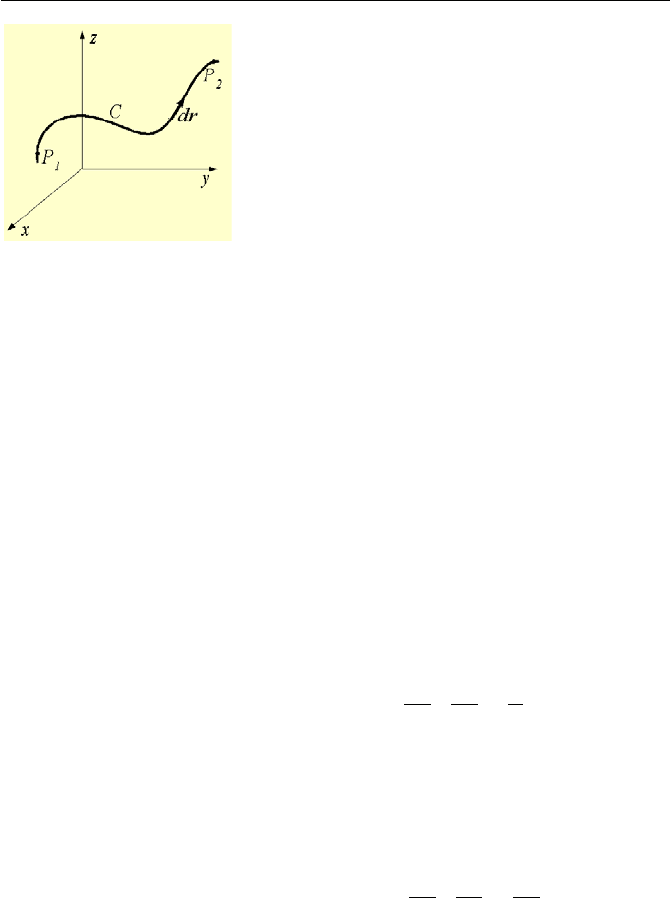
Line integral of a vector along the segment path C, shown in Figure VIIc.1.6,
is defined as:
2
1
()
P
xyz
P
C
Adr Adx Ady Adz
´
µ
¶
⋅= + +
³
K
K
VIIc.1.19
952 VIIc. Engineering Mathematics: Vector Algebra
Figure VIIc.1.6. Line integral along a segment in Cartesian coordinate system
which indicates the path-dependence of line integrals. For example, consider the
intersection of surface z = xy
2
and plane z = 1. We would like to integrate vector
kzyjxziyA
K
K
K
K
33
3 −+= along this segment from point P
1
located at 1, 1, 1 to
point P
2
located at 0.25, 2, 1. We first find the dot product of the vector by the
elemental segment as:
zydzdyxzydxrdA −+=⋅
3
3
K
K
Since z = xy
2
= 1 this results in dz = 0. Taking the derivative of the function repre-
senting the segment:
02
2
=+ xydydxy
from this equation, we find dx = – xdy/y. Substituting for x from xy
2
= 1, we ob-
tain dx = – dy/y
3
. Therefore, the integral of the dot product becomes:
1
2
33
2
1
2
1
22
3
2
1
2
1
−=
µ
µ
¶
´
»
¼
º
«
¬
ª
=+−=−+=⋅
=
=
=
=
³³
y
y
y
y
P
P
P
P
y
y
dy
y
dy
zydzdyxzydxrdA
K
K
To verify that the result depends on the path, we may assume a different path con-
necting the same points P
1
and P
2
, such as z = xy
3
. In this case, the derivative of
the function representing the path becomes y
3
dx + 3xy
2
dy = 0. Hence, we have dx
= –3xdy/y. Substituting for x, the derivative becomes dx = –3dy/y
4
. Finally
3
4
93
2
1
2
1
233
3
2
1
2
1
−=
µ
µ
¶
´
»
»
¼
º
«
«
¬
ª
=+−=−+=⋅
=
=
=
=
³³
y
y
y
y
P
P
P
P
yy
dy
y
dy
zydzdyxzydxrdA
K
K
Special Case. Now, consider a case where vector
A
K
is gradient of a potential
function (i.e.
fA ∇=
K
K
) (recall that 0=×∇ A
K
K
). In this case, the line integral be-
comes independent of the path and depends only on the end points P
1
and P
2
. To
demonstrate, we substitute the gradient in Equation VIIc.1.19. This results in the
