Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.


2. Analytical Solutions to Differntial Equations 933
wavelength (
λ
), and wave velocity (c). The introduction of Plank’s constant (h =
6.62559
× 10
-34
J·s) in 1901 allowed the introduction of particle properties such
as energy (E = h
v
), momentum (M = E/c=h
v
), and relativistic mass (m = W/c
2
= h
v
/c
2
) into the description of the electromagnetic waves. Hence, a photon
would have a wavelength given by Mh
/=
λ
.
In 1924, De Broglie extended this definition of wavelength to other particles.
Hence, such particles as electron, proton, neutron, or any other subatomic particle
having momentum M, would have a “De Broglie wavelength” given by
Mh
/=
λ
. Equation VIIb.1.32 gives the general time-dependent form of the
Shroedinger wave equation. This equation predicts the behavior of the probability
amplitude (
ψ
) of a particle having a mass of m and potential energy V as a func-
tion of position and time. We now solve Equation VIIb.1.32 for the spherical
waves. Such waves represent, for example, a scattered particle by a nucleus or the
emission of an
α
ray from the parent nucleus. The differential equation to solve
is given by Equation VIIb.1.32, repeated here:
t
tr
itrrVtr
m ∂
∂
=+∇−
),(
),()(),(
2
2
2
K
=
K
G
K
=
ψ
ψψ
VIIb.1.32
where ʄ = h/2
π
. This equation, therefore, describes the wave behavior of a parti-
cle having mass m in a field that induces potential energy V(r). Since we consider
the potential energy to be only a function of location, we are able to separate vari-
ables and obtain a set of spatial and temporal functions by defining
ψ
as:
)()(),( trtr
ξ
ϕ
ψ
KK
=
VIIb.2.28
so that time is expressed as a separate factor, then the phase of
ψ
at any instant is
the same throughout the entire wave. Such waves are called standing waves.
Substituting for
ψ
in Equation VIIb.1.32, we get:
t
t
rirtrVrt
m
∂
∂
=+∇−
)(
)()()()()()(
2
2
2
ξ
ϕϕξϕξ
K
=
K
G
K
=
If we divide both sides of this equation by that given by Equation VIIb.2.28, we
get:
E
t
t
t
irVr
rm
=
∂
∂
=+∇−
)(
)(
1
)()(
)(
1
2
2
2
ξ
ξ
ϕ
ϕ
=
G
K
K
=
where E is the total energy of the state. The time-independent Shroedinger equa-
tion is then obtained as:
0)()]([
2
)(
2
2
=−+∇ rrVE
m
r
K
G
=
K
ϕϕ
VIIb.2.29
The simplest case to investigate is the atom of hydrogen where an electron is
orbiting the nucleus at a distance r, having an electrostatic potential energy of –
e
2
/r. In the solution below, we leave the potential energy in its general form of
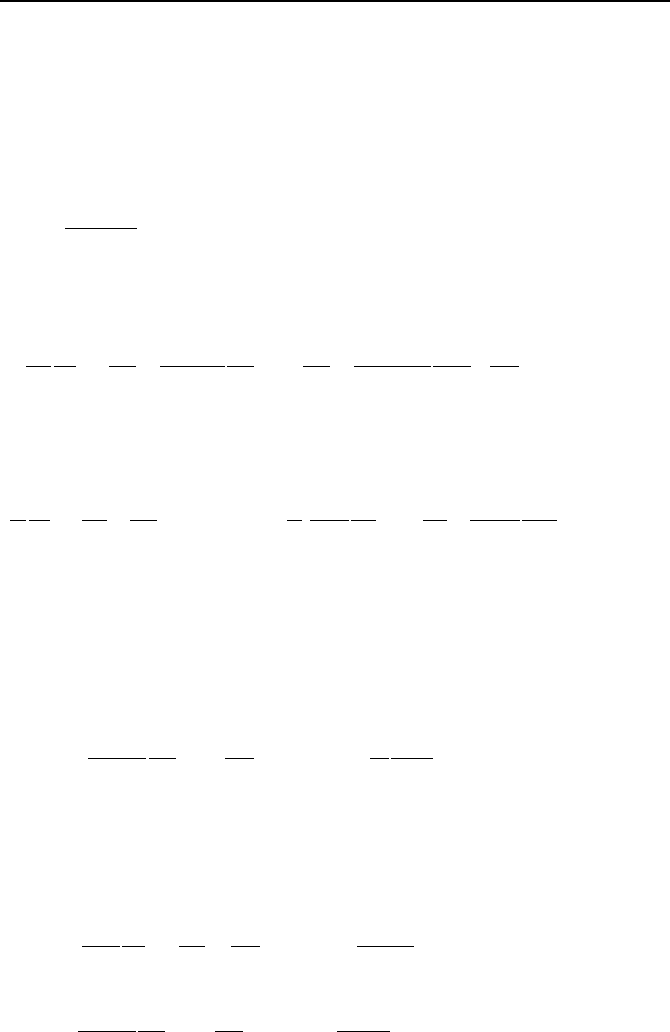
934 VIIb. Engineering Mathematics: Differential Equations
In the solution below, we leave the potential energy in its general form of V(r). To
further simplify the solution, rather than writing the equation for both electron and
nucleus, we solve the time independent Shroedinger equation in the spherical co-
ordinate system whose origin is at the center of mass. Since the nucleus is much
more massive than the electron, the center of mass is very close to the nucleus. In
this case, mass m in Equation VIIb.2.29 represents the mass of electron and nu-
cleus and is given by:
ne
ne
mm
mm
m
+
=
Substituting for the Laplacian operator (see Section VIIc.1.1), Equation VIIb.2.29
for a system representing both the electron and the hydrogen nucleus becomes:
0)]([
2
sin
1
)(sin
sin
1
)(
1
22
2
222
2
2
=−+
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
ϕ
φ
ϕ
θ
θ
ϕ
θ
θ
θ
ϕ
rVE
m
rr
r
r
r
r
=
Again, we may use the method of separation of variables if potential energy is
only a function of r. For
),()(),,(
φ
θ
φ
θ
ϕ
SrRr = , the equation can be separated
as:
]
sin
1
)(sin
sin
1
[
1
)]([
2
)(
1
2
2
2
2
2
2
φθ
θ
θ
θθ
∂
∂
+
∂
∂
∂
∂
−=−+
SS
S
rrVE
m
dr
dR
r
dr
d
R
=
VIIb.2.30
For this relation to hold, both sides of this equation must be equal to some con-
stant. We call this separation constant l(l+1) because the differential equation of
the wave function in the
θ
direction is a Legendre differential equation. Before
proceeding to solve for R, let’s use the same method of the separation of variables
for the right side of Equation VIIb.2.30. In this case, we use
)()(),(
φθφθ
ΦΘ=S
to get:
2
2
2
1
)]1()(sin
sin
1
[sin
φ
θ
θ
θθ
θ
d
d
ll
d
d
d
d
Φ
Φ
−=++
Θ
Θ
Again, for this relation to hold, both sides must be equal to some constant such as
n
2
. To summarize, we managed to break down the Shroedinger partial differential
equation into three ordinary differential equations for radial, polar, and azimuthal
directions:
Radial:
0]
2
)1(
)([
2
)(
1
2
22
2
2
=
+
−−+ =
=
m
r
ll
rVE
m
dr
dR
r
dr
d
Rr
VIIb.2.31
Polar:
0
sin
)1()(sin
sin
1
2
2
=−++
Θ
Θ
θ
θ
θ
θθ
n
ll
d
d
d
d
VIIb.2.32

2. Analytical Solutions to Differntial Equations 935
Azimuthal: 0
2
2
2
=Φ−
Φ
n
d
d
φ
VIIb.2.33
These equations are valid if the potential energy V(r) is spherically symmetric and
if l and n, referred to as quantum numbers, are suitably chosen. The solution to
the azimuthal differential equation is straightforward and is given as
)exp()exp(
21
φφ
incinc −+=Φ . The integer n is known as the magnetic quantum
number because the energy of the hydrogen atom depends on this quantum num-
ber only if the atom is placed in a magnetic field. If the atom is placed in a mag-
netic field, then distinct values for n determine the allowed energy levels.
We now try to find the solution to the polar differential equation. To see if this
equation can be cast in the form of Equation VIIb.1.7, we make a change of vari-
able as
θ
cos=x . We find the required derivative terms from:
dx
d
dx
d
Θ
−=
θ
θ
sin
and
dx
d
dx
d
d
d
Θ
−
Θ
=
Θ
θθ
θ
cossin
2
2
2
2
2
.
Substituting into Equation VII.2.32, it simplifies to:
0
sin
)1(sin
sin
1
2
2
=Θ
»
»
¼
º
«
«
¬
ª
−++
»
¼
º
«
¬
ª
Θ
θ
θ
θ
θθ
n
ll
d
d
d
d
VIIb.2.34
We can now carry out the derivative of the first term in Equation VIIb.2.34 to get:
0
sin
)1(
sin
cos
2
2
2
2
=Θ
»
»
¼
º
«
«
¬
ª
−++
Θ
+
Θ
θ
θθ
θ
θ
n
ll
d
d
d
d
We now substitute for the derivative terms in terms of
θ
cos=x , which yields:
0
sin
)1(sin
sin
cos
cossin
2
2
2
2
2
=Θ
»
»
¼
º
«
«
¬
ª
−++
¸
¹
·
¨
©
§
Θ
−+
Θ
−
Θ
θ
θ
θ
θ
θθ
n
ll
dx
d
dx
d
dx
d
where we have used dy/d
θ
= (dy/dx)(dx/d
θ
). Collecting terms and substituting for
2
1sin x−=
θ
, we get:
0
1
)1(2)1(
2
2
2
2
2
=Θ
»
»
¼
º
«
«
¬
ª
−
−++
Θ
−
Θ
−
x
n
ll
dx
d
x
dx
d
x VIIb.2.35

936 VIIb. Engineering Mathematics: Differential Equations
If there is no magnetic field, then n = 0 (hence, =Φ constant) and Equa-
tion VIIb.2.35 can be simplified to Equation VIIb.1.7. If l takes distinct integers
such as 0, 1, 2, 3, etc., then l(l+1) = 0, 2, 6, 12, etc.
In Equation VIIb.2.35, constant l is known as the angular-momentum quantum
number. To have a satisfactory answer for the wave function, n must have integral
values between –l and +l. For example, for l = 3, n can be –3, -2, -1, 0, 1, 2,
and 3.
Finally, the solution to the radial differential equation can be obtained by mak-
ing a change in function from R(r) to R(r) = Y/r:
0]
2
)1(
)([
2
2
2
22
2
=
+
−−+ Y
mr
ll
rVE
h
m
dr
Yd
=
This is a linear second order differential equation similar to the one-dimensional
wave equation. The final solution for the probability amplitude is then found as:
rrYr
nnl
/)()()(),,(
φθφθψ
ΦΘ=
3. Pertinent Functions and Polynominals
We now briefly discuss such important functions and polynomials as Dirac delta-
function, the Gaussian error function, the Gamma function, and the Bessel func-
tions.
Dirac
δ
-function. This function is defined as:
¯
®
=∞
≠
=−
0
0
0
,
,0
)(
xx
xx
xx
δ
,
³
∞
∞−
=− 1)(
0
dxxx
δ
The most useful property of the Dirac
δ
-function is when integrated along a well-
behaved function f(x):
³
)()()(
00
xfdxxfxx =−
δ
Error function. The Gaussian error function is used in such engineering ap-
plications as conduction heat transfer and reliability engineering. The Gaussian
Error function is defined as:
³
dzexerf
xz
0
2
2
)(
−
=
π
Note that the complementary error function is erfc(x) = 1 – erf(x) (i.e., the integral
limits are from x to
∞).
Gamma function is defined by the integral:
³
∞
−−
=Γ
0
1
)( dttex
xt

3. Pertinent Functions and Polynominals 937
Note the following property of the gamma function Γ(z + 1) = zΓ(z). It can be
verified that
Γ(1/2) = (
π
)
1/2
, Γ(0) = ∞, Γ(1) = ",1 , Γ(n) = (n – 1)!
Exponential integrals are obtained by sustituting values for the index n in the
following integral:
µ
¶
´
=
∞
−
1
)( dt
t
e
xE
n
xt
n
For example, E
0
(x) = e
–x
/x and
(
)
)1/()()(
1
−−=
−
−
nxxEexE
n
x
n
. Also
)()(
1
xExE
nn −
−=
′
.
Bessel functions, having engineering applications in cylindrical coordinates for
nuclear reactor core design, thermal conduction and electricity, are solutions of the
Bessel differential equation:
0)(
22
2
2
2
=−++ yvx
dx
dy
x
dx
yd
x VIIb.3.1
This second order differential equation is of order v and has the following general
solution:
)()()(
21
xYCxJCxy
vv
+=
where real functions J
v
and Y
v
are referred to as Bessel functions of the first and
the second kind of order v, respectively.
Modified Bessel functions: The complex form of the Bessel function is ob-
tained if x is replaced by ix:
0)(
22
2
2
2
=+−+ yvx
dx
dy
x
dx
yd
x
The solution to this equation is given as:
)()()(
43
xKCxICxy
vv
+=
where real functions I
v
and K
v
are called the modified Bessel functions of the first
and second kind. The Bessel functions of the first and the second kind are of the
following form:
¦
∞
=
+
++Γ
−
=
0
2
2
)1(!2
)1(
)(
m
vm
mm
v
v
mvm
x
xxJ
)sin(
)()cos()(
)(
π
π
v
xJvxJ
xY
vv
v
−
−
=
Bessel functions of order v = 0 and v = 1 are used more frequently. The polyno-
mial for the Bessel function of the first kind of order 0 is given as (Abramowitz):

938 VIIb. Engineering Mathematics: Differential Equations
8
12
108642
0
105,33
)3/(0002100.0
)3/(0039444.0)3/(444479.0)3/(3163866.0)3/(2656208.1)3/(2499997.21)(
−
×<≤≤−
++
−+−+−=
ε
ε
x
x
xxxxxxJ
The polynomial for the Bessel function of the first kind of order 1 is given as:
8
1210
8642
1
1
103.1,33
)3/(00001109.0)3/(0031761.0
)3/(00443319.0)3/(03954289.0)3/(21093573.0)3/(56249985.05.0)(
−
−
×<≤≤−
++−
+−+−=
ε
ε
x
xx
xxxxxJx
The polynomial for the Bessel function of the second kind of order 0 is given as:
8
12108
642
00
104.1,30
)3/(00024846.0)3/(00427916.0)3/(04261214.0
)3/(25300117.0)3/(74350384.0)3/(60559366.036746691.0)()2/ln()/2()(
−
×<≤≤
+++−
+−++=
ε
ε
π
x
xxx
xxxxJxxY
The polynomial for the Bessel function of the second kind of order 1 is given as:
7
12108
642
11
101.1,30
)3/(0027873.0)3/(0400976.0)3/(3123951.0
)3/(3164827.1)3/(1682709.2)3/(2212091.06366198.0)()2/ln()/2()(
−
×<≤≤
++−+
−++−=
ε
ε
π
x
xxx
xxxxJxxxxY
The polynomial for the modified Bessel function of the first kind of order 0 is
given as:
7
1210
8642
0
106.175.375.3
)75.3/(0045813.0)75.3/(0360768.0
)75.3/(2659732.0)75.3/(2067492.1)75.3/(0899424.3)75.3/(5156229.31)(
−
×<≤≤−
+++
++++=
ε
ε
x
xx
xxxxxI
The polynomial for the modified Bessel function of the first kind of order 1 is
given as:
9
1210
8642
1
1
10875.375.3
)75.3/(00032411.0)75.3/(0301532.0
)75.3/(2658733.0)75.3/(15084934.0)75.3/(51498869.0)75.3/(878906.05.0)(
−
−
×<≤≤−
+++
++++=
ε
ε
x
xx
xxxxxIx
The polynomial for the modified Bessel function of the second kind of order 0, is
given as:
8
12108
642
0
101,20
)2/(00000740.0)2/(00010750.0)2/(00262698.0
)2/(03488590.0)2/(23069756.0)2/(42278420.057721566.0)()2/ln()(
−
×<<<
+++
++++−−=
ε
ε
x
xxx
xxxxIxxK
o
The polynomial for the modified Bessel function of the second kind of order 1, is
given as:
9
12108
642
11
108,20
)2/(00004686.0)2/(00110404.0)2/(01919402.0
)2/(18156897.0)2/(67278579.0)2/(15443144.01)()2/ln()(
−
×<<<
+−−−
−−++=
ε
ε
x
xxx
xxxxIxxxxK
3. Pertinent Functions and Polynominals 939
Abramowitz gives polynomials for x outside the ranges shown above. Some use-
ful derivatives of Bessel functions are as follows:
Derivatives of J
0
(x), Y
0
(x), I
0
(x), and K
0
(x):
)(
)(
1
0
xJ
dx
xdJ
−= )(
)(
1
0
xY
dx
xdY
−=
)(
)(
1
0
xI
dx
xdI
−= )(
)(
1
0
xK
dx
xdK
−=
Derivatives of J
v
(x), Y
v
(x), I
v
(x), and K
v
(x):
2/])([
)(
11 +−
−=
vv
v
JxJ
dx
xdJ
2/])([
)(
11 +−
−=
vv
v
YxY
dx
xdY
2/])([
)(
11 +−
−=
vv
v
IxI
dx
xdI
2/])([
)(
11 +−
−=
vv
v
KxK
dx
xdK
Derivatives of x
v
J
v
(x), x
v
Y
v
(x), x
v
I
v
(x), and x
v
K
v
(x):
)(
)(
1
xJx
dx
xJdx
v
v
v
v
−
= )(
)(
1
xYx
dx
xYdx
v
v
v
v
−
=
)(
)(
1
xIx
dx
xIdx
v
v
v
v
−
= )(
)(
1
xKx
dx
xKdx
v
v
v
v
−
−=
Derivatives of x
-v
J
0
, x
-v
Y
0
, x
-v
I
0
, and x
-v
K
0
:
)(
)(
1
xJx
dx
xJdx
v
v
v
v
+
−
−
−= )(
)(
1
xYx
dx
xYdx
v
v
v
v
+
−
−
−=
)(
)(
1
xIx
dx
xIdx
v
v
v
v
+
−
−
= )(
)(
1
xKx
dx
xKdx
v
v
v
v
+
−
−
−=
Some useful integrals of Bessel functions are as follows:
³
+−= cxJdxxJ )()(
01
³
+−= cxYdxxY )()(
01
³
+−= cxIdxxI )()(
01
,
³
+−= cxKdxxK )()(
01
³
+=
−
cxJxdxxJx
v
v
v
v
)()(
1
,
³
+−=
−
+
−
cxJxdxxJx
v
v
v
v
)()(
1
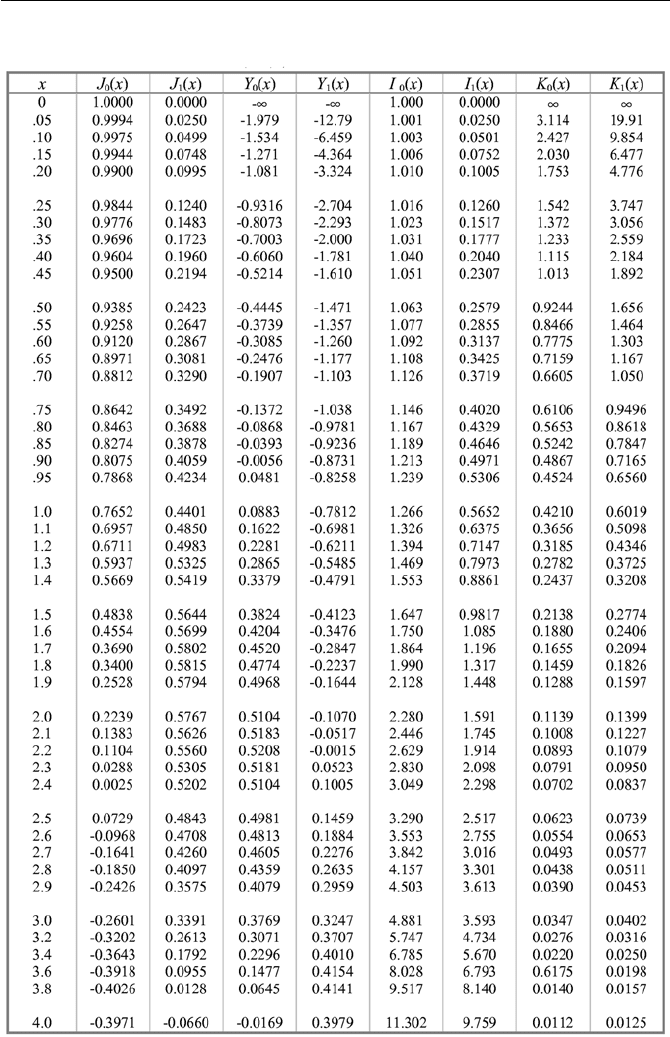
Table VIIb.3.1 includes some Bessel functions for the range of 0 ≤ x ≤ 4 and
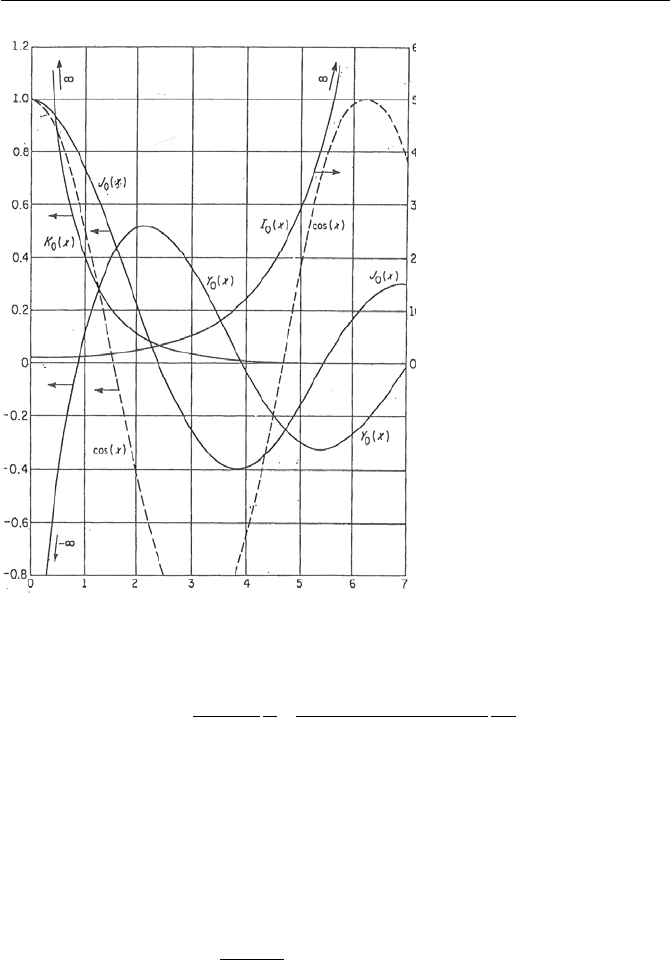
Figure VIIb.3.1 shows Bessel functions of order zero for the range of 0
≤ x ≤ 7.
Hankel functions: are obtained from the Bessel functions and defined as:
)()(
1,
xiYxJH
vvv
+=
)()(
2,
xiYxJH
vvv
−=
Jacobi polynomial is the solution to the special Jacobi differential equation.
The Jacobi polynomial is:
940 VIIb. Engineering Mathematics: Differential Equations
Table VIIb.3.1. Bessel functions
3. Pertinent Functions and Polynominals 941
Figure VIIb.3.1. Bessel functions of order zero for the range of 0 ≤ x ≤ 7
"+
+
+++−
+
+
−=
!2)1(
)1)(()1(
!1
)(
1),,(
2
x
aa
bnbnnnx
a
bnn
xbaP
Jacoby
Chebyshev polynomial of the first kind is given as:
"−−
¸
¸
¹
·
¨
¨
©
§
+−
¸
¸
¹
·
¨
¨
©
§
−==
−−− 224221
)1(
4
)1(
2
)coscos()( xx
n
xx
n
xxnxP
nnn
Chebyshev
Hermite polynomial is the solution to the Hermite differential equation and is
given by Rodrigue’s formula:
n
xn
xn
Hermite
dx
ed
exP
2
2
)1()(
−
−=
Hyperbolic functions are defined as sinh(x) = (e
x
– e
–x
)/2 and cosh(x) =
(e
x
+ e
–x
)/2.

942 VIIb. Engineering Mathematics: Differential Equations
Legendre polynomials are the solution to the Legendre differential equation
and are given as:
2
1(1)
()
2!
nn
Legendre
nn
dx
Px
ndx
−
=
It can be verified that P
0
(x) =1, P
1
(x) = x, P
2
(x) = (3x
2
– 1)/2, P
3
(x) = (5x
3
– 3x)/2,
etc. Also
1
''
1
2
() ()
21
nn nn
PxP xdx
n
δ
+
−
´
µ
µ
¶
=
+
The recurrence relations for Legendre polynomials are as follows:
0)()()12()()1(
11
=++−+
−+
xnPxxPnxPn
nnn
)()1()()(
1
xPnxPxxP
nnn
+=
′
−
′
+
Associated Lengendre polynomials are obtained from the following formula:
)()1()(
2/2
xP
dx
d
xxP
l
m
m
mm
l
−=
and the spherical harmonics are given by:
θ
ϕ
π
im
llm
eP
ml
mll
Y )(cos
)!(4
)!)(12(
)(
2/1
¸
¸
¹
·
¨
¨
©
§
+
−+
=Ω
K
Lagurre polynomials are the solution to the Lagurre differential equation and
are given as:
n
xnn
x
Lagurre
dx
exd
exP
)(
)(
−
=
