Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

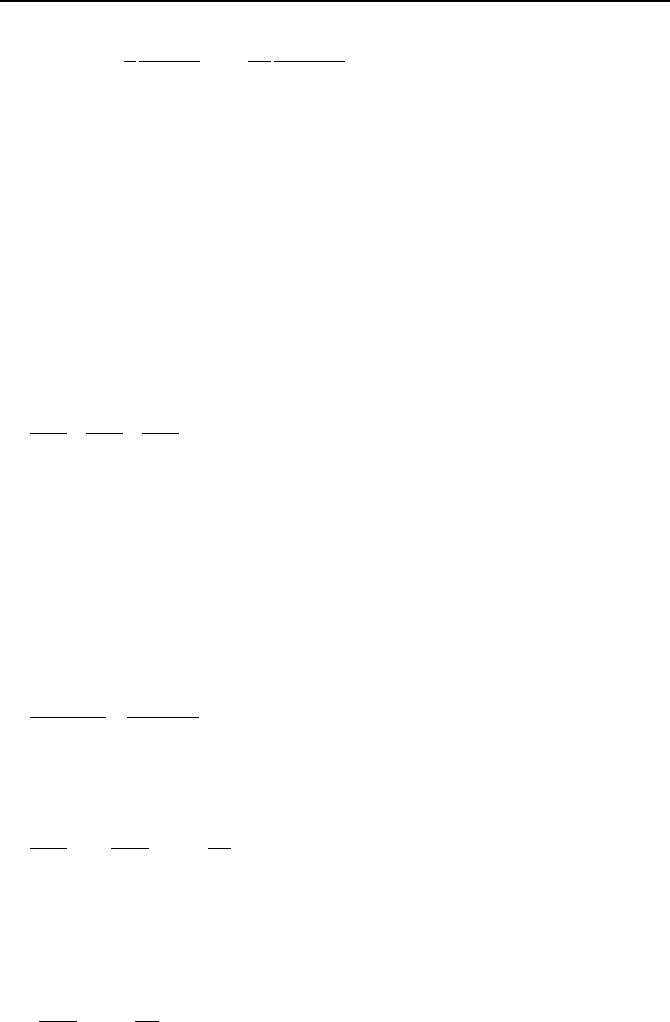
1. Definition of Terms 903

]

)(

[]

)0(

[)(

−

Differential equation is an equation that relates two or more dependent vari-

ables in terms of derivatives. Formulating the behavior of many physical phe-

nomena by a mathematical model results in differential equations as discussed in

Section 2.

Ordinary differential equation is a differential equation in which all deriva-

tives are taken with respect to a single independent variable. For example, the dif-

ferential equation d

y/dx

+ f(x)dy/dx + g(x)y = h(x) is an ordinary differential

equation.

Partial differential equation is a differential equation that contains at least one

partial derivative with respect to some dependent variable. For example, the dif-

ferential equation:

=∇=

∂

VIIa.1.1

(known as Laplace equation) is a partial differential equation. In Equa-

tion VIIa.1.1,

∇ is the Laplacian operator, as discussed in Chapter VIIc.

Exact differential is a first-order differential equation in the form of M(x, y)dx

+ N(x, y) dy = 0 (also called perfect differential) if and only if a function f(x, y) ex-

ists so that df(x, y) = M(x, y)dx + N(x, y)dy. For exact differential equations df(x,

y) = 0. Hence, f(x, y) = C. If such a function exists,

dyyxNdxyxM ),(),( +

also called an exact differential. The necessary and sufficient condition for an ex-

pression to be an exact differential is that

yxN

yxM

∂

∂ ),(),(

Order of a differential equation is the highest order derivative in the differen-

tial equation. For example,

)()(

xQyx

=+++

is a differential equation of order three.

Degree of a differential equation is the power of the highest order derivative.

For example, the following differential equation:

)(4

is of order four and degree three.

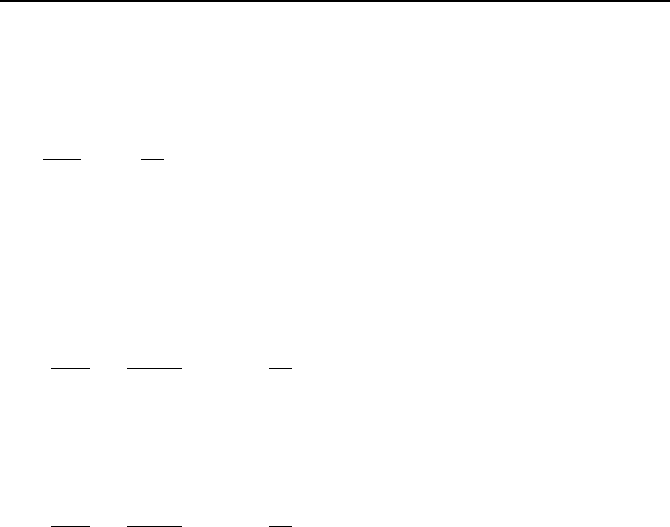
904 VIIa. Engineering Mathematics: Fundamentals

Linear differential equations are those in which no dependent variable ap-

pears in the form of a product by itself or any of its derivatives. For example,

Equation VII.a.1.1 is a linear differential equations while the following differential

equation:

)()()(

xhyxg

y =++

is a nonlinear differential equation due to the first term in the left side, which in-

cludes the product of the dependent variable y and its derivative.

Homogeneous differential equation is a linear equation when all its terms in-

clude either the dependent function or one of its derivatives. Hence, the following

is a homogeneous differential equation:

=++++

−

Non-homogeneous differential equations are equations that include a term

that is a function of only the independent variable. Therefore, the following is a

non-homogeneous differential equation:

)(

xqyc

=++++

−

" VIIa.1.2

for

0)( ≠xq

. However, if q(x) = 0 then Equation VIIa.1.2 becomes a homogene-

ous differential equation.

Homogeneous boundary condition is a boundary condition when the depend-

ent variable or its derivatives, or any linear combination of the dependent variable

and its derivatives, vanishes at the boundary. For example, if at x = a, y(a) = 0,

then the boundary condition at x = a is a homogeneous boundary condition. Simi-

larly, boundary conditions y’(a) = 0 and c

y(a) + c

y’(a) = 0 are also homogeneous

boundary conditions whereas, boundary conditions y(a) = b, or c

y(a) + c

y’(a) = b

are nonhomogeneous boundary conditions.

Trivial solution is any homogeneous differential equation subject to homoge-

neous boundary conditions that always has a solution in the form of y(x) = 0. This

solution, referred to as the trivial solution, is usually of no interest.

General or homogeneous solution to a differential equation is a non-trivial

function for the dependent variable that satisfies the homogeneous differential

equation. For example, the general solution to dy/dx = 2 should satisfy dy/dx = 0.

The general solution is, therefore, y = C. This is also shown as y

= C. General

solutions to various differential equations are discussed in Section 3.

Particular solution to a differential equation is a solution that satisfies the non-

homogeneous equation. For example, a particular solution to dy/dx = 2 is y

= 2x.

Finding particular solutions relies on the type of the function q(x), in Equa-

1. Definition of Terms 905

tion VIIa.1.2. For example, q(x) may be of an algebraic, trigonometric, or expo-

nential function:

exq

axaxxq

xxxxq

:)(

cos,sin:)(

,,,1:)(

or a combination of all the above functions.

Complete solution to a differential equation is the summation of the homoge-

neous and the particular solutions. For example, the general solution to dy/dx = 2

is y = y

+ y

= 2x + C. Since the solution must also satisfy the boundary or initial

conditions, the value of the constants of integration should be obtained from the

specified boundary or initial conditions (when x represents time).

Initial-value problems are differential equations that require particular solu-

tions so that the function and its derivatives all satisfy a specified set of conditions

corresponding to the same value of the independent variable. For example, the

general solution to an nth-order linear differential equation has n arbitrary con-

stants. These constants should be determined from n specified sets of conditions.

In initial-value problems, these specified sets of conditions require that y(x

) = a,

y’(x

) = b, y”(x

) = c, etc. where a, b, ",c are specified constants. The differen-

tial equation of displacement of mass in a spring – dashpot system is an initial

value problem where initial conditions at a specified time are used to determine

constants of integration.

Boundary-value problems are differential equations that require particular so-

lutions so that the function and its derivatives satisfy a specified set of conditions.

In boundary-value problems, the several values of the function or its derivatives

are not all known at the same independent variable, rather at different values of

the independent variable. For example, the general solution to an nth-order linear

differential equation has n arbitrary constants. These constants can be determined

from n specified sets of conditions at point x = a

through point x = a

. Certain

classes of boundary-value problems fall in the category of the characteristic-value

or eigenvalue problems as discussed later. Determination of the deflection of a

simply supported beam, thermal conduction, and wave equation are examples of

boundary-value problems.

Total differential of a function of several variables, such as f(x,y,z), is defined

as:

∂

provided that the partial derivatives are continuous. In general, the variables x, y,

and z can themselves be functions of the independent variables s and t. In this

case, the variables x, y, and z are referred to as the intermediate variables and the

partial derivative of f with respect to s becomes:

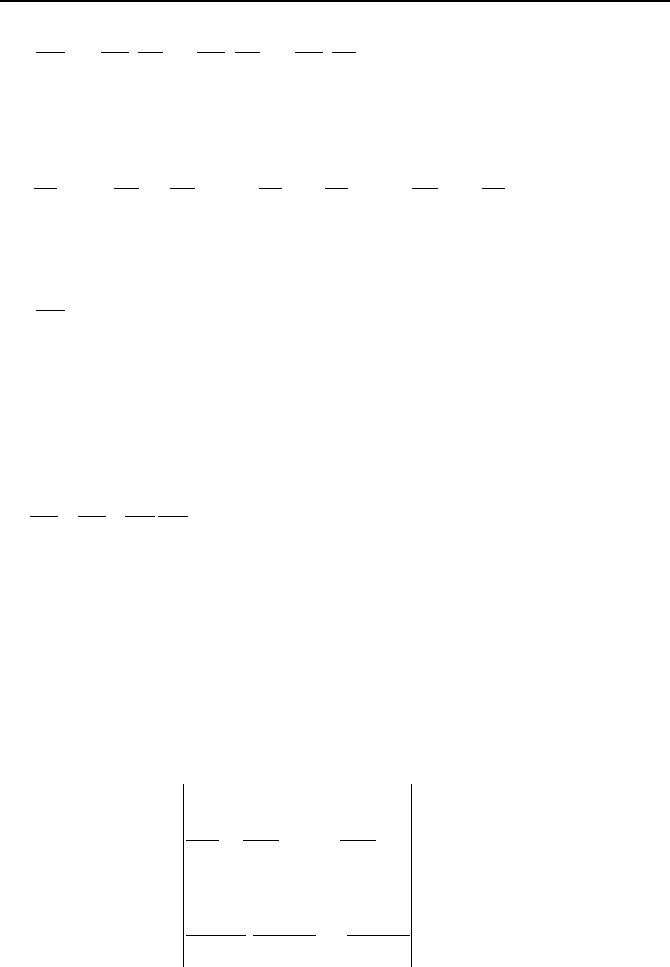
906 VIIa. Engineering Mathematics: Fundamentals

tttt

)()()()(

∂

where the subscript t implies that the derivatives are carried out with respect to s

only. For example, for the function f[x(t,s),y(t,s),z(t,s)] = xy + z

x + y

z, we can

carry the derivative of f with respect to s as:

)2()2()()(

∂

If the intermediate variables are given as x = 2s, y = st, and z = t, we can then find

the partial derivative of f with respect to s as:

)2()2()2()(

yztzxty

+++=

∂

This equation can be further simplified if the intermediate variables are substituted

in terms of independent variables.

Chain rule for derivatives follows the total differential defined above. Con-

sider a composite function such as F = f[s, U(s)]. According to the chain rule for

taking the derivative of composite functions, dF/ds is:

∂

Linear dependence of n functions is given by

()cf x+

()cf x++"

()

cf x. If at least one constant coefficient (c

) is nonzero then the linear de-

pendence is nontrivial. These functions are linearly independent in the domain ab

(i.e.,

bxa ≤≤ ) if, over the domain, no function is linearly dependent on the other

functions. For example, x, sin x and xy are linearly independent over any domain

while sin

x, cos

x, and –1 are linearly dependent over any domain.

Wronskian determinant of n functions, f

through f

, is defined as:

),,,(

−

∂

fnff

fffW

For function f

through f

to be linearly independent over a specific domain, it is

necessary that the Wronskian determinant is not equal zero over that domain.

However, if the Wronskian determinant vanishes in a specific domain, it does not

necessarily mean that the related functions are linearly dependent.

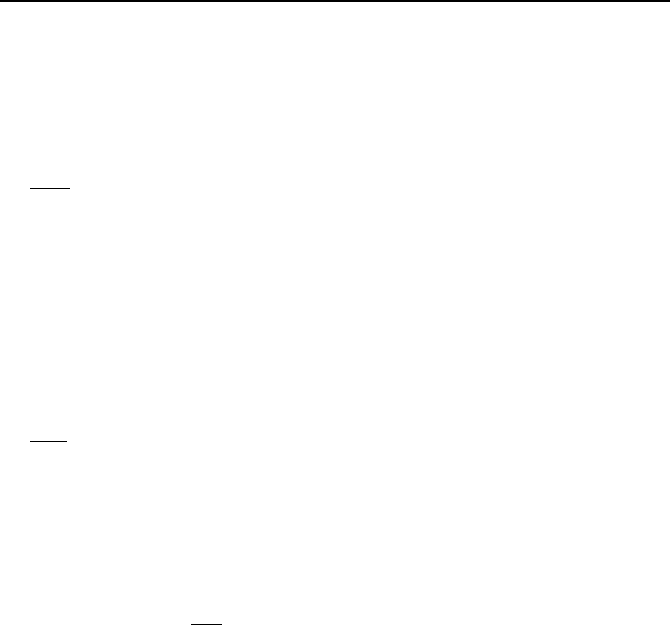
1. Definition of Terms 907

Eigenvalue or characteristic-value problems are special cases of the bound-

ary-value problems having particular solutions in periodic forms. Problems deal-

ing with classical wave equation, quantum mechanics, elasticity, and vibration are

characteristic-value problems. To elaborate the characteristic-value problems,

consider the following differential equation:

=+ y

VIIa.1.3

which is subject to homogeneous boundary conditions y(0) = 0 and y(L) = 0. This

equation has a solution in the form of:

xcxcy cossin

From the first boundary condition, c

= 0. From the second boundary condition c

= 0. We, therefore, find y = 0 which is a trivial solution. Now consider the fol-

lowing differential equation:

=+ y

VIIa.1.4

subject to the same boundary conditions. The solution to this equation is

.cossin

xcxcy

λλ

+= From the first boundary condition, c

= 0. From the

second boundary condition

πλ

= where n = 1, 2, 3, ",4 and the solution

to the differential equation becomes

nnn

= where )/sin( Lxn

πϕ

= . Hence:

ccy

nnnn

sin== VIIa.1.5

Comparing these two differential equations and related solutions, we conclude that

in the case of Equation VIIa.1.4, the second boundary condition was actually used

to determine the parameter

. The reason we were able to obtain a nontrivial so-

lution for Equation VIIa.1.4 is that certain values of

, as given by Ln /

cause the determinant of the coefficients to vanish. Equation VIIa.1.4 is a charac-

teristic-value equation. Values obtained for

are called characteristic or eigen-

values and the corresponding solutions (

) are called the characteristic or eigen-

functions.

In problems dealing with mechanical vibration, the eigenvalues give the natural

frequency of the system. The knowledge of natural frequencies of a load bearing

system is essential. To avoid failure, external loads should not be applied at or

near these frequencies as resonance will cause an amplification of displacement,

leading to failure. An interesting aspect of the characteristic value equations is the

fact that we now have to determine many more unknown coefficients (i.e., c

, c

, ",

c ), yet no more boundary conditions are left. In the next definition, we’ll

see how we can use the orthogonality aspect of the eigenfunctions to our advan-

tage.

908 VIIa. Engineering Mathematics: Fundamentals

Orthogonality of characteristic functions is where the scalar product of two

vectors is zero, as discussed in Section 5. Having this in mind, we now consider

two functions, y

(x) and y

(x) and a weighting function, r(x). These functions are

orthogonal in the interval (a, b), with respect to the weighting function r(x), if the

integral of their product over the given interval vanishes:

dxxxxr 0)()()(

ϕϕ

The characteristic functions are orthogonal. To verify, we may use the above ex-

ample by assuming r(x) = 1:

0sinsin

ππ

An important aspect of the orthogonal functions is the ability to expand arbitrary

functions in terms of orthogonal functions. If a set of functions such as

are or-

thogonal in the interval (a, b) with respect to the weighting function r(x), then an

arbitrary function f(x) can be expanded in terms of these functions as:

=+++=

∞

221100

)()()()()(

xcxcxcxcxf

ϕϕϕϕ

If such expansion exists, then we may multiply both sides by the following func-

tions and integrate over the above interval to get:

∞

nknk

dxxxxrcdxxxfxr

)()()()()()(

ϕϕϕ

VIIa.1.6

Using the orthogonality property of the eigenfunctions, the integral on the left side

becomes zero except for k = n. Therefore, Equation VIIa.1.6 reduces to:

[]

³³

nnn

dxxxrcdxxxfxr

)()()()()(

ϕϕ

From here we can find the unknown coefficients c

, c

, ",

c . For the charac-

teristic equation of a matrix see Chapter VIId.

Fourier transform. It can be shown that any reasonably well-behaved func-

tion, f(x) can be represented in the interval –L, L by a series of trigonometric func-

tions such as sines or cosines. Indeed it can be shown that any piecewise differen-

tiable function in the interval –L, L can be represented by both sine and cosine

functions of a common period 2L, i.e.:

LxL

AAxf

<<−

++=

∞

sincos)(

ππ

where the coefficients are given as:

1. Definition of Terms 909

−

dxxf

A )(

−

cos)(

−

sin)(

Laplace transform is a mathematical conversion to simplify operations. To

convert a function such as f(t) by this means, we multiply the function by exp(-st)

and take the integral from zero to infinity:

{}

∞

−

)()( dtetftf

The advantage of this type of conversion is that exponential and trigonometric

functions are transformed into simple algebraic functions. This simplifies the in-

tegration task. For example, the reader may verify that

{}

()

sinsin

dtateat

∞

−

A and

{}

()

coscos

dtateat

∞

−

It is important to note that the conversion of a function by Laplace transform is a

linear conversion. Therefore, we conclude that:

{}{}{}

)()()()(

2121

tfbtfatbftaf AAA +=+

{}

+++−=



−

−−

)0()0(

)0()(

)(

nnn

sfstfs

tfd

"AA

VIIa.1.7

{}{}

)(

)]([ tf

tuf AA =

{

}

{}

)()( atftfe

−= AA

{}

[]

tfd

tft

)(

)1()(

−=

{}{ }

)()()()(

tftfduufutf AAA =



−

∞

910 VIIa. Engineering Mathematics: Fundamentals

{}

³³



)(

dttf

dttf AA

In this text, the Laplace transform of a function is shown as

{}

ftf

)(

=A . The

Laplace transforms of some exponential and trigonometric functions are presented

in Table VIIa.1.1

Table VIIa.1.1. Laplace transforms of some familiar functions

Function,

)(tf Transform, f

1 1/s

t 1/s

n-1

/(n-1)! 1/s

−

1/(s + a)

n-1

- at

/(n-1)! 1/(s + a)

)/()( baee

atbt

−−

1/(s + a)(s + b)

)/()( abaebe

atbt

−−

s/(s + a)(s + b)

sin at a/(s

+ a

)

cos at s/(s

+ a

)

sinh at a/(s

– a

)

cosh at s/(s

– a

)

t sin at 2as/(s

+ a

)

t cos at (s

– a

)/(s

+ a

)

sin at – at cos at 2a

/(s

+ a

)

t sinh at 2as/(s

– a

)

t cosh at (s

+ a

)/(s

– a

)

at cosh at – sinh at 2a

/(s

– a

)

ate

sin

−

a/[a

+ (s + b)

]

ate

cos

−

(s+b)/[a

+ (s + b)

]

sin at cosh at – cos at sinh at 4a

/(s

+ 4a

)

sin at sinh at 2a

s/(s

+4a

)

sinh at – sin at 2a

/(s

– a

)

cosh at – cos at 2a

s/(s

– a

)

)(t

)(

tt −

exp(–st

)

)(t

′

)('

tt −

sexp(–st

)

n!/s

n+1

n-1

/(n – 1)! 1/s

n-1

-at

/(n – 1)! 1/(s + a)

[(n – 1) – at)] t

n-2

-at

/(n – 1)! s/(s + a)

1. Famous Differential Equations 911

VIIb. Differential Equations

This chapter includes two types of differential equations used in most engineering

applications and applied physics. These are the ordinary and the partial differen-

tial equations, ODE and PDE, respectively. We begin with the ordinary differen-

tial equations.

1. Famous Differential Equations

In this section several differential equations often used in engineering applications

are discussed. Solutions to some ordinary differential equations are discussed in

Section 2.

1.1. Ordinary Differential Equations

Bernoulli differential equation: The following equation is known as the Ber-

noulli differential equation:

yxQyxP

)()(

=+ VIIb.1.1

where n may have any real value. Unless n is 0 or 1, the Bernoulli differential

equation is non-linear. The Bernoulli differential equation appears in such fields

as the study of population dynamics and hydrodynamic stability. The Bernoulli

differential equation can be transformed into a linear differential equation by a

change of dependent variable from y to z = y

1– n

to obtain:

)()1()()1( xQnzxPn

−=−+

resulting in a first-order linear differential equation, the solution of which is pre-

sented in Section 2 of this chapter.

Riccati differential equation: This is another first order non-linear differen-

tial equation named after Italian mathematician J. F. Riccati, and has the following

form:

)()()(

xRyxQyxP

=++ VIIb.1.2

For R(x) = 0, Equation VIIb.1.2 becomes the Bernoulli differential equation (n =

2) with z = 1/y transforming it to a first-order linear differential equation. If u(x)

is one solution to the Riccati differential equation, the substitution y = u(x) + 1/z

will transform the Riccati equation:

)(2)]()([ xPzxQxuP

=+−

912 VIIb. Engineering Mathematics: Differential Equations

into a first-order linear differential equation. Since there is no general rule to

solve non-linear differential equations analytically, a change of variable, as dem-

onstrated for Bernoulli and Riccati differential equations, is an effective means of

solving such classes of non-linear equations.

Euler-Cauchy differential equation: This is a linear, non-homogeneous dif-

ferential equation with coefficients being functions of the independent variable.

Euler-Cauchy equation has the form of:

)(

xqyc

=++++

−

" VIIb.1.3

This equation can be transformed into an nth-order linear differential equation by

a change of the independent variable from x to

xz ln= . The solution to Equa-

tion VIIb.1.3 is presented in Section 2.

Special Class of Differential Equations

Famous differential equations used in many engineering applications can be de-

rived from ordinary second-order differential equations written in the general form

of:

0)(

)(

)1(

=+++++ yxQQ

xPP

VIIb.1.4

Some examples are as follows.

Jacobi differential equation is given as:

0)()]1([)1(

=+++−+− ynbn

bxa

VIIb.1.5

The solution to the Jacobi differential equation is the Jacobi polynomial as dis-

cussed in Section 4. A special case of the Jacobi equation is:

0)1()1(

=−++−− ycnn

Chebyshev differential equation is obtained from the special form of the

Jacobi equation if c = 1:

0)1(

=+−− yn

VIIb.1.6

The solution to this equation is known as Chebyshev’s polynomials.

Laguerre differential equation is a second-order linear differential equation

given as: