Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.


2. Numerical Solutions of Ordinary Differential Equations 983
),(
)
2
,
2
(
)
2
,
2
(
),(
34
23
12
1
xkyxxfk
k
x
y
x
xfk
k
x
y
x
xfk
yxfk
ii
ii
ii
ii
∆+∆+=
∆
+
∆
+=
∆
+
∆
+=
=
The same example is solved with the fourth-order Runge – Kutta method and the
results are summarized in Table VIIe.2.4.
Table VIIe.2.4. The fourth-order Runge-Kotta method ( 1.0=∆x )
x y
Runge - Kutta
y
Analytical
0.0 0.5000000 0.5
0.1 0.6110508 0.611052
0.2 0.7488653 0.748868
0.3 0.9215829 0.921589
0.4 1.1391452 1.139156
0.5 1.4136948 1.413711
0.6 1.7600627 1.760087
By this method, the error at x = 0.6 is now reduced to 0.001%. Data for Ta-
ble VIIe.2.4 are produced by FORTRAN program VIIe.2.2, included on the ac-
companying CD-ROM.
2.2. Methods Based on Predictor-Corrector
There are several methods based on the predictor-corrector concept such as the
modified Euler method, Adams method, and Milne method.
The Modified Euler Method
In the marching technique, as used in the Euler method, the value at each subse-
quent increment is calculated from the derivative at the previous increment (i.e.,
y
n+1
is obtained from
'
n
y rather than
'
1
+n
y ). In the modified Euler method, to bet-
ter represent the function in the chosen interval,
)(xy
′
is obtained at the average
of
'
n
y and
'
1
+n
y . Since the value of
'
1
+n
y is not known before hand, an iterative
process must be used. The approach in the modified Euler method is as follows:
Predictor:
)()()(
1 iii
xyxxyxy
′
∆+=
+
VIIe.2.1
Corrector:
)]()([
2
)()(
11 ++
′
+
′
∆
+=
iiii
xyxy
x
xyxy VIIe.2.2
The corrector (Equation VIIe.2.2) can alternatively be written as:

984 VIIe. Engineering Mathematics: Numerical Analysis
)],(),([
2
)()(
)(
1
11
k
i
iiiii
yxfyxf
x
xyxy
+
++
+
∆
+= VIIe.2.3
where in Equation VIIe.2.3, k is the iteration index and is placed inside the paren-
theses to emphasize that it is not an exponent for y. To demonstrate the modified
Euler method, let’s apply the predictor-corrector concept to the same example
used in Section 2.1. For this purpose, we substitute:
),(2
2
yxfxy
dx
dy
=+=
into Equation VIIe.1.3 to obtain:
)]2()2([
2
)(
1
2
1
2
)1(
1
k
i
iiii
k
i
yxyx
x
yy
+
+
+
+
+++
∆
+=
To find the starting value (i.e.
0
1
y ) we use the Predictor (i.e. Equation VIIe.2.1).
Using an interval size of
05.0=∆x , the iterations for y
1
progress as follows:
=
0
1
y 0.5 + 0.05 (0 + 2 × 0.5) = 0.55
=
1
1
y 0.5 + 0.025 [(0 + 2 × 0.5) + (0.05
2
+ 2 × 0.55)] = 0.5525625
=
2
1
y 0.5 + 0.025 [(0 + 2 × 0.5) + (0.05
2
+ 2 × 0.5525625)] = 0.5526906
=
3
1
y 0.5 + 0.025 [(0 + 2 × 0.5) + (0.05
2
+ 2 × 0.5526906)] = 0.55269700
=
4
1
y 0.5 + 0.025 [(0 + 2 × 0.5) + (0.05
2
+ 2 × 0.55269700)] = 0.55269730
=
5
1
y 0.5 + 0.025 [(0 + 2 × 0.5) + (0.05
2
+ 2 × 0.55269730)] = 0.55269730
In this case, the iteration converged in five steps. Generally, however, we stop the
process after the specified convergence criterion is met, then we proceed to calcu-
late y
2
, y
3
, ",
4
y until the specified interval is covered.
For higher accuracy, we may choose a smaller increment such as 0.01, 0.001,
etc. The results obtained from the modified Euler method for
05.0=∆x ,
01.0=∆x , and 001.0=∆x are shown in Table VIIe.2.5. The data for Ta-
ble VIIe.1.4 are produced by FORTRAN program Table VIIe.1.2, included on the
accompanying CD-ROM.
Table VIIe.2.5. The modified Euler method
x
05.0=∆x 01.0=∆x 001.0=∆x
y
Analytical
0.0 0.5000000 0.5000000 0.5000000 0.5000000
0.1 0.6112050 0.6110582 0.6110521 0.611052
0.2 0.7492421 0.7488834 0.7488687 0.748868
0.3 0.9222736 0.9216164 0.9215894 0.921589
0.4 1.1402705 1.1392002 1.1391562 1.139156
0.5 1.4154136 1.4137793 1.4137121 1.413711
0.6 1.7625828 1.7601872 1.7600888 1.760087

3. Numerical Solution of Partial Differential Equations 985
The Milne Method
In this method the predictor – corrector are as follows:
Predictor:
)](2)()(2[
3
4
)()(
2131 −−−+
′
+
′
−
′
∆
+=
iiiii
xyxyxy
x
xyxy VIIe.2.4
Corrector:
)]()(4)([
3
)()(
1111 −+−+
′
+
′
+
′
∆
+=
iiiii
xyxyxy
x
xyxy VIIe.2.5
The Adams–Bashforth Method
In this method the predictor – corrector are as follows:
Predictor:
)](9)('37)(59)(55[
24
)()(
32131 −−−−+
′
−+
′
−
′
∆
+=
iiiiii
xyxyxyxy
x
xyxy VIIe.2.6
Corrector:
)]()(5)(19)(9[
24
)()(
2111 −−++
′
+
′
−
′
+
′
∆
+=
iiiiii
xyxyxyxy
x
xyxy VIIe.2.7
In the first glance, the Milne and the Adams-Bashford equations look complicated
and convey laborious computation. However, these are simple relations for pro-
gramming and once coded, they can be used for any function and with any step
size increment.
3. Numerical Solution of Partial Differential Equations
Most second-order partial differential equations for engineering applications have
a general form of:
0),,,,(
2
22
2
2
=
∂
∂
∂
∂
+
∂
∂
+
∂∂
∂
+
∂
∂
x
y
x
y
uyxD
y
u
C
yx
u
B
x
u
A
Depending on the value of B
2
– 4AC, the equation may be of elliptic, parabolic, or
hyperbolic type:
If B
2
– 4AC < 0 the differential equation is elliptic
If B
2
– 4AC = 0 the differential equation is parabolic
If B
2
– 4AC > 0 the differential equation is hyperbolic
We can alternatively describe differential equations of the elliptic type as having
the general form of the diffusion equation:
)()()()()( rSrrqrrp
K
K
K
K
K
=+∇−∇
φφ
VIIe.3.1

986 VIIe. Engineering Mathematics: Numerical Analysis
If 0)( =rq
K
and
=)(rp
K
constant, Equation VIIe.3.1 becomes the Poisson equation
as introduced in Chapter VIIb. If
0)()( == rSrq
K
K
, Equation VIIe.3.1 becomes the
Laplace equation.
Similarly, partial differential equations of the parabolic type are in the general
form of:
)(),(),(),(),(
),(
rStrtrqtrtrp
t
tr
K
K
K
K
K
K
+−∇∇=
∂
∂
φφ
φ
VIIe.3.2
Finally, partial differential equations of the hyperbolic type are in the form of the
wave equation:
)(
2
2
2
2
2
2
2
2
2
z
u
y
u
x
u
t
u
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
α
VIIe.3.3
To solve any of the elliptic, parabolic, or hyperbolic type partial differential equa-
tions numerically, we replace the derivatives by a difference quotient. To demon-
strate the difference equivalent of a second order derivative, we make use of the
Taylor series to expand
)( xxf
i
∆− and )( xxf
i
∆+ about point x and assume that
the function has a continuous fourth derivative:
"+∆+∆
′′′
−∆
′′
+∆
′
−=∆−
432
24
)(
6
)(
2
)(
)()()( x
xf
x
xf
x
xf
xxfxfxxf
i
iv
ii
iii
Similarly
"+∆+∆
′′′
+∆
′′
+∆
′
+=∆+
432
24
)(
6
)(
2
)(
)()()( x
xf
x
xf
x
xf
xxfxfxxf
i
iv
ii
iii
We now sum these expansions to get:
2
11
2
x
fff
f
iii
i
∆
+−
=
′′
−+
The error in ignoring the remaining terms is of the order of
2
x∆ . Similarly, we
can use central difference approximation to represent the first derivative as:
x
ff
f
ii
i
∆
−
=
′′
−+
2
11
with the same error of order
2
x∆ as for the second derivative.
3.1. Elliptic Equations
An example of the elliptic partial differential equation is the steady-state heat con-
duction equation. In this section, we use two slightly different methods of solving
this equation numerically. The first method uses the derived conduction equation
in the form of a Laplace equation and applies the difference approximation where
3. Numerical Solution of Partial Differential Equations 987
∆x
∆y
x
i
x
i+1
x
i+2
x
i-1
x
i-2
y
j
y
j+1
y
j+2
y
j-1
y
j-2
y
j-3
i,j i+1,ji-1,j
i,j-1
i,j+1
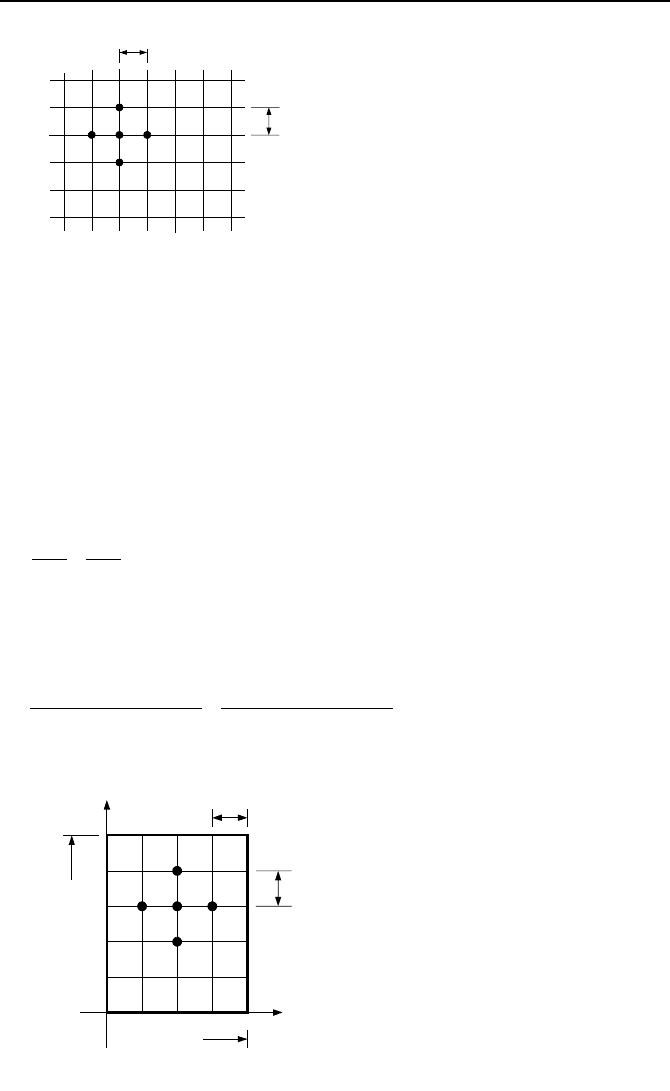
Figure VIIe.3.1. Subdivision of a region in the xy-plane
∆
∆
x
y
T = 20 CT = 20 C
T = 120 C
T = 20 C
x=4 cm
y
=5 cm
1
2
12
7
8
9
456
10
11
3
Figure VIIe.3.2. Temperature distribution in a homogeneous plate
in the second method, we show how to derive the heat conduction equation in dif-
ference form.
Solving the Laplace Equation
First, to demonstrate the solution of partial differential equations by difference ap-
proximation, consider the two-dimensional Laplace equation:
0
2
2
2
2
=
∂
∂
+
∂
∂
y
u
x
u
We now subdivide the region of interest into incremental values (Figure VIIe.3.1).
The Laplace equation becomes:
0
)(
2
)(
2
2
1,,1,
2
,1,,1
=
∆
+−
+
∆
+−
+−+−
y
uuu
x
uuu
jijijijijiji
VIIe.3.4

988 VIIe. Engineering Mathematics: Numerical Analysis
If for simplicity we assume that the x increment and the y increments are equal, we
get the algorithm as:
04
1,1,,,1,1
=++−+
+−+− jijijijiji
uuuuu VIIe.3.5
or equivalently:
)(25.0
1,1,,1,1, +−+−
+++=
jijijijiji
uuuuu
implying that the dependent value at each node is the arithmetic average of the de-
pendent value of all the neighboring nodes. As an example, we may use Equa-
tion VIIb.3.5 to find nodal temperatures in the interior of a plate made of a homo-
geneous material, having all the four boundary temperatures as shown in
Figure VIIe.3.2. Using an equal increment of 1 cm for both x and y axes, we ob-
tain the following sets of equations for nodes 1 through 12.
For node number 1:
404
421
−=++− TTT
For node number 2:
204
5231
−=+−+ TTTT
For node number 3:
404
632
−=+− TTT
For node number 4:
204
7541
−=++− TTTT
For node number 5:
04
86542
=++−+ TTTTT
For node number 6:
204
9653
−=+−+ TTTT
For node number 7:
204
10874
−=++− TTTT
For node number 8:
04
119875
=++−+ TTTTT
For node number 9:
204
12986
−=+−+ TTTT
For node number 10:
1404
11107
−=+− TTT
For node number 11:
1204
1211108
−=+−+ TTTT
For node number 12:
1404
12119
−=−+ TTT
Since this is a set of linear algebraic equations, we can arrange it in a matrix as
follows:
3. Numerical Solution of Partial Differential Equations 989
1 2 3 4 5 6 7 8 9 10 11 12
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
−
−
−
−
−
−
−
−
−
−
=
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
−
−
−
−
−
−
−
−
−
−
−
−
140
120
140
20
0
20
20
0
20
40
20
40
41010
0000000
041010000000
004101000000
100410100000
010041010000
001004101000
000100410100
000010041010
0000010041
01
000000100410
000000010141
000000001014
12
11
10
9
8
7
6
5
4
3
2
1
12
11
10
9
8
7
6
5
4
3
2
1
T
T
T
T
T
T
T
T
T
T
T
T
As pointed out in Chapter VIId, there are several ways to solve this matrix equa-
tion including matrix inversion and Gauss-Seidel iteration. Solving this set of
equations, we find the determinant of the coefficient matrix to be equal to 0.414E7
and the value of T
1
through T
12
(in Centigrade) as:
T
1
T
2
T
3
T
4
T
5
T
6
T
7
T
8
T
9
T
10
T
11
T
12
23.3 24.7 23.3 28.7 32.0 28.7 39.5 46.0 39.5 63.1 73.1 63.1
Expectedly, the temperature of nodes 1, 4, 7, and 10 are the same as temperature
of nodes 3, 6, 9, and 12. Hence, we could reduce the number of equations by tak-
ing advantage of symmetry.
Let’s now solve a similar problem but this time as shown in Figure VII.3.3, the
boundary conditions are specified such that there is no symmetry to reduce the
number of equations. Following the same procedure outlined for the previous ex-
ample, we find the following matrix equation:
∆
∆
x
y
T = 150 CT = 50 C
T = 200 C
T = 50 C
x=4 cm
y
=5 cm
1
2
12
7
8
9
4
56
10
11
3
Figure VIIe.3.3. Temperature distribution in a heterogeneous plate

990 VIIe. Engineering Mathematics: Numerical Analysis
1 2 3 4 5 6 7 8 9 10 11 12
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
−
−
−
−
−
−
−
−
−
−
=
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
−
−
−
−
−
−
−
−
−
−
−
−
350
200
50
150
0
50
150
0
50
200
50
100
410100000000
041010000000
004101000000
100410100000
010041010000
001004101000
000100410100
000010041010
00000
1004101
000000100410
000000010141
000000001014
12
11
10
9
8
7
6
5
4
3
2
1
12
11
10
9
8
7
6
5
4
3
2
1
T
T
T
T
T
T
T
T
T
T
T
T
We expect to get the lowest temperature at node 1 and the highest temperature at
node 12. Here are the results, in Centigrade, for this case:
T
1
T
2
T
3
T
4
T
5
T
6
T
7
T
8
T
9
T
10
T
11
T
12
63.6 78.1 100 76.3 99.0 122 92.4 120 138 123 151 160
We may use the same method to solve similar problems for other boundary tem-
peratures or other mesh sizes such as 0.1 cm. Smaller mesh sizes give more de-
tailed information about temperature distribution in the plate.
Direct Derivation of The Heat Conduction Equation
In the above examples, we used the Laplace equation to solve two cases that dealt
only with temperature boundary condition. In the second method, we will derive
the conduction equation in its difference form.
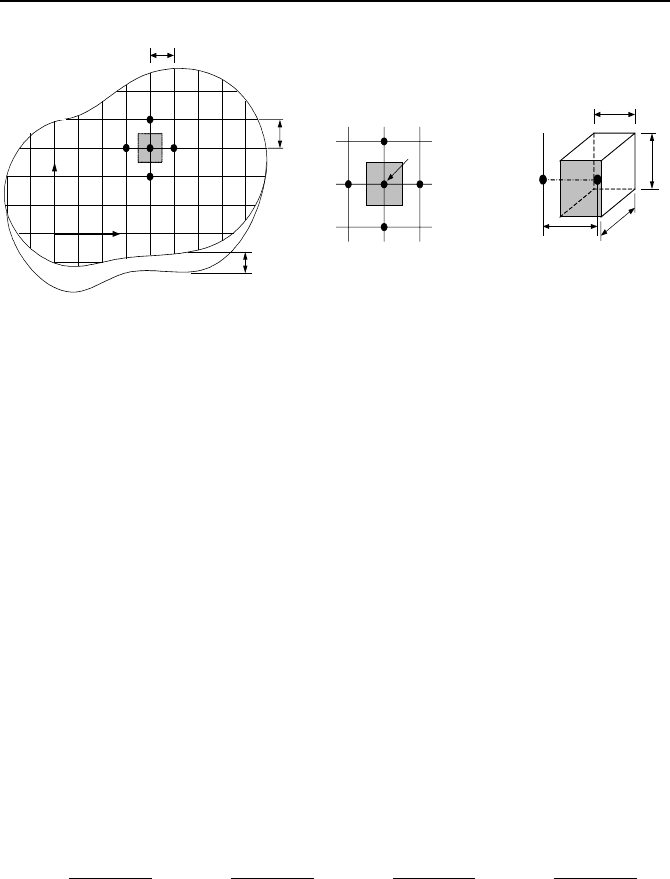
To do this, we use an arbitrary node such as node x
i
, y
j
for the medium shown
in Figure VIIe.3.4. This node represents the shaded rectangle, one side at
x∆ and
the other at
y∆
. In this method, we also consider an additional term for internal
heat generation.
3. Numerical Solution of Partial Differential Equations 991
∆ x
∆ y
x, i
y, j
x
i
, y
j
x
i+1
, y
j
x
i
, y
j+1
x
i
, y
j-1
x
i-1
, y
j
x
i
, y
j
∆ x
∆
y
∆
z = 1
∆ x
x
i-1
, y
j
∆ z = 1
Figure VIIe.3.4. Determination of temperature distribution by direct derivation of heat
conduction equation
In the Cartesian coordinate system, the adjacent nodes that exchange heat with
node (x
i
, y
j
) are nodes (x
i-1
, y
j
), (x
i+1
, y
j
), (x
i
, y
j-1
) and (x
i
, y
j+1
). For simplicity, we
refer to these nodes by using only their indices hence, (x
i
, y
j
) is node (i, j), etc.
Each node in the center of a shaded area (parallelepiped of unit depth) represents
the temperature of that area. This shows that in order to have more accurate tem-
perature distribution, we should use a smaller mesh size or increment. Also note
that we are using a unit depth which makes the temperature distribution two-
dimensional. Generally, we must also consider temperature distribution in the z-
direction, in other words, we should solve a three-dimensional problem. We now
apply the first law of thermodynamics to the two-dimensional problem of Fig-
ure VIIe.3.5, using each shaded area as a control volume with unit depth
perpendicular to the plane of Figure VIIe.3.5. The first law states that in steady
state, summation of the rate of heat transfer from all of the adjacent nodes plus the
rate of internal heat generation must be equal to zero:
0V
,,1,,1,,,1,,1
=
′′′
++++
→+→−→+→− jijijijijijijijiji
qQQQQ
If there is no internal heat generation, by substituting from the Fourier’s law of
heat conduction we get:
0)1()1()1()1(
,1,,1,,,1,,1
=
∆
−
×∆+
∆
−
×∆+
∆
−
×∆+
∆
−
×∆
+−+−
y
TT
xk
y
TT
xk
x
TT
yk
x
TT
yk
jijijijijijijiji
If we assume equal increments in the x and y directions, this equation reduces to
Equation VIIe.3.5 as derived from the Laplace equation. Having derived the algo-
rithm for interior nodes, we can proceed with the derivation of corner nodes and
nodes exposed to convection boundary conditions shown in Figure VIIe.3.6.
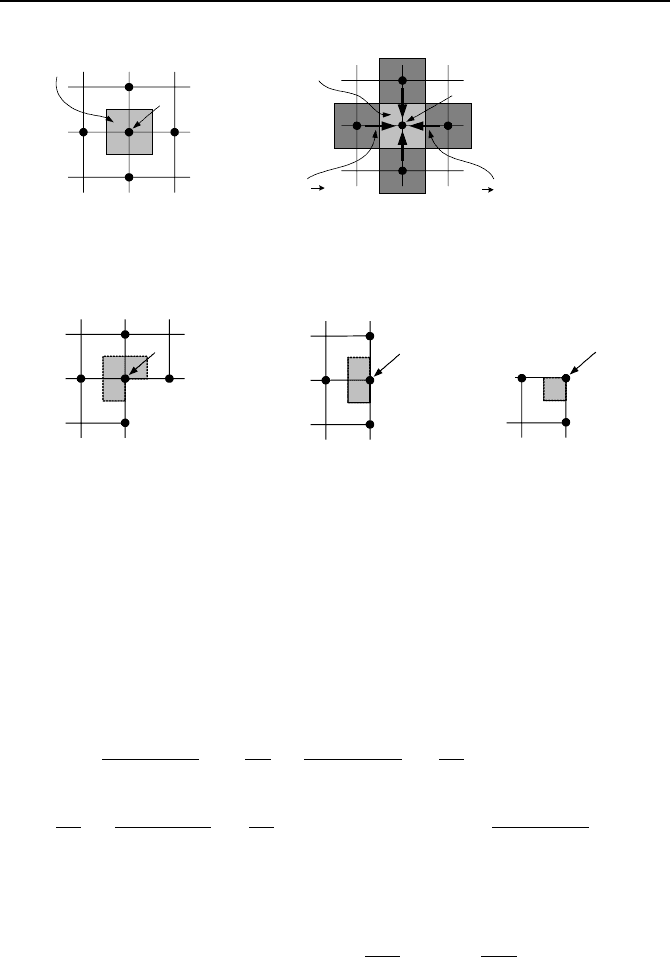
992 VIIe. Engineering Mathematics: Numerical Analysis
x
i
, y
j
x
i+1
, y
j
x
i
, y
j+1
x
i
, y
j-1
x
i-1
, y
j
i, j
i+1, j
i, j+1
i, j-1
i-1, j
q
i+1 j - i, j
.
q
i-1, j i, j
.
.
q
"'
.
q
"'
Figure VIIe.3.5. Nodal heat transfer in steady state two - dimensional conduction
x
i
, y
j
x
i+1
, y
j
x
i
, y
j+1
x
i
, y
j-1
x
i-1
, y
j
h, T
f
x
i
, y
j
x
i
, y
j+1
x
i
, y
j-1
h, T
f
x
i-1
, y
j
(a)
(b)
x
i
, y
j
x
i
, y
j-1
h, T
f
x
i-1
, y
j
(c)
Figure VIIe.3.6. (a) Node at interior corner, (b) node at plane surface, and (c) node at ex-
ternal corner
For the internal corner node with convection of Figure VIIe.3.6(a), we must
consider heat conduction from half of the area and heat convection from the rest of
the area for nodes i, j – 1 and i + 1, j. The rate of heat transfer from nodes i – 1, j
and i, j+ 1 is the same as iven by Equation VIIe.3.4:
0)1())(1
2
()1
2
(
))(1
2
()1
2
()1(
,1,
,
,1,
,
,,1,,1
=
∆
−
×∆+
»
»
¼
º
«
«
¬
ª
−×
∆
+
∆
−
×
∆
+
»
»
¼
º
«
«
¬
ª
−×
∆
+
∆
−
×
∆
+
∆
−
×∆
+−
+−
y
TT
xkTT
x
h
y
TT
x
k
TT
y
h
x
TT
y
k
x
TT
yk
jiji
jif
jiji
jif
jijijiji
If the mesh sizes or increments are the same ( )yx ∆=∆ , we can simplify this
equation to obtain:
fjijijijiji
T
k
xh
T
k
xh
TTTT
∆
−=
∆
+−+++
−++−
2)3(2)()(2
,1,,11,,1
VIIe.3.6
or the node at the plane surface with the convection boundary, Figure VIIe.3.5(b),
we must consider heat conduction from half of the area and heat convection from
the rest of the area for nodes i, j – 1 and i, j + 1. The rate of heat transfer from
node i – 1, j is the same as Figure VIIe.3.5(a):
