Маслова Т.Н., Суходский А.М. Справочник школьника по математике. 5-11 кл
Подождите немного. Документ загружается.

ÀËÃÅÁÐÀ
§ 10. Ïðåîáðàçîâàíèå òðèãîíîì. âûðàæåíèé
ÀËÃÅÁÐÀ
Ðàçäåë II. ÂÛÐÀÆÅÍÈß
117
116
,
2
sin
2
sin2coscos
b-ab+a
-=b-a
(4)
,
coscos
)
(
sin
tgtg
b
a
b
+a
=
b
+a
(5)
.
coscos
)
sin
(
tgtg
b
a
b
-a
=
b
-a
(6)
Ôîðìóëû (5) è (6) âåðíû ïðè
,ba è
îòëè÷íûõ îò
.,
2
ZÎp+
p
kk
Ï ð è ì å ð. Ïðåîáðàçîâàòü â ïðîèçâåäåíèå
.12cos48cos
oo
-
q Ïðèìåíèâ ôîðìóëó ðàçíîñòè êîñèíóñîâ (4) ïðè
,12,48
oo
=b=a
ïîëó÷èì
=
-+
-=-
2
1248
sin
2
1248
sin212cos48cos
oooo
oo
.18sin30sin2
oo
-=
Òàê êàê
,5,030sin =
o
òî îêîí÷àòåëüíî ïîëó÷èì
.18sin12cos48cos
ooo
-=-
n
86. Ïðåîáðàçîâàíèå ïðîèçâåäåíèÿ òðèãîíîìåò-
ðè÷åñêèõ ôóíêöèé â ñóììó. Ñïðàâåäëèâû ñëåäóþ-
ùèå ôîðìóëû:
,
2
)
(
sin
)
(
sin
cossin
b
+a+
b
-a
=
b
a
(1)
,
2
)(cos)(cos
sinsin
b+a-b-a
=ba
(2)
.
2
)(cos)(cos
coscos
b+a+b-a
=ba
(3)
Ï ð è ì å ð. Ïðåîáðàçîâàòü â ñóììó
.19cos43sin
oo
q Âîñïîëüçîâàâøèñü ôîðìóëîé (1) ïðè
,43
o
=a
,19
o
=b
ïîëó÷èì
=
++-
=
2
)1943(sin)1943(sin
19cos43sin
oooo
oo
).62sin24(sin
2
1
oo
+=
n
87. Ïðåîáðàçîâàíèå âûðàæåíèÿ
tbta sincos +
ê âèäó
.tA )(sin a+
Ëþáîå âûðàæåíèå âèäà
+ta cos
tb sin+
ìîæíî ïðåäñòàâèòü â âèäå
).(sin a+tA
Äëÿ
ýòîãî âûíåñåì çà ñêîáêè âûðàæåíèå
22
ba +
è ïî-
ëó÷èì
=+ tbta sincos
.sincos
2222
22
÷
÷
ø
ö
ç
ç
è
æ
+
+
+
+=
t
ba
b
t
ba
a
ba
Íî
.1
2
22
2
22
=
÷
÷
ø
ö
ç
ç
è
æ
+
+
÷
÷
ø
ö
ç
ç
è
æ
+ ba
b
ba
a
Ýòî çíà÷èò, ÷òî
ÀËÃÅÁÐÀ
§ 10. Ïðåîáðàçîâàíèå òðèãîíîì. âûðàæåíèé
ÀËÃÅÁÐÀ
Ðàçäåë II. ÂÛÐÀÆÅÍÈß
117
116
,
2
sin
2
sin2coscos
b-ab+a
-=b-a
(4)
,
coscos
)
(
sin
tgtg
b
a
b
+a
=
b
+a
(5)
.
coscos
)
sin
(
tgtg
b
a
b
-a
=
b
-a
(6)
Ôîðìóëû (5) è (6) âåðíû ïðè
,ba è
îòëè÷íûõ îò
.,
2
ZÎp+
p
kk
Ï ð è ì å ð. Ïðåîáðàçîâàòü â ïðîèçâåäåíèå
.12cos48cos
oo
-
q Ïðèìåíèâ ôîðìóëó ðàçíîñòè êîñèíóñîâ (4) ïðè
,12,48
oo
=b=a
ïîëó÷èì
=
-+
-=-
2
1248
sin
2
1248
sin212cos48cos
oooo
oo
.18sin30sin2
oo
-=
Òàê êàê
,5,030sin =
o
òî îêîí÷àòåëüíî ïîëó÷èì
.18sin12cos48cos
ooo
-=-
n
86. Ïðåîáðàçîâàíèå ïðîèçâåäåíèÿ òðèãîíîìåò-
ðè÷åñêèõ ôóíêöèé â ñóììó. Ñïðàâåäëèâû ñëåäóþ-
ùèå ôîðìóëû:
,
2
)
(
sin
)
(
sin
cossin
b
+a+
b
-a
=
b
a
(1)
,
2
)(cos)(cos
sinsin
b+a-b-a
=ba
(2)
.
2
)(cos)(cos
coscos
b+a+b-a
=ba
(3)
Ï ð è ì å ð. Ïðåîáðàçîâàòü â ñóììó
.19cos43sin
oo
q Âîñïîëüçîâàâøèñü ôîðìóëîé (1) ïðè
,43
o
=a
,19
o
=b
ïîëó÷èì
=
++-
=
2
)1943(sin)1943(sin
19cos43sin
oooo
oo
).62sin24(sin
2
1
oo
+=
n
87. Ïðåîáðàçîâàíèå âûðàæåíèÿ
tbta sincos +
ê âèäó
.tA )(sin a+
Ëþáîå âûðàæåíèå âèäà
+ta cos
tb sin+
ìîæíî ïðåäñòàâèòü â âèäå
).(sin a+tA
Äëÿ
ýòîãî âûíåñåì çà ñêîáêè âûðàæåíèå
22
ba +
è ïî-
ëó÷èì
=+ tbta sincos
.sincos
2222
22
÷
÷
ø
ö
ç
ç
è
æ
+
+
+
+=
t
ba
b
t
ba
a
ba
Íî
.1
2
22
2
22
=
÷
÷
ø
ö
ç
ç
è
æ
+
+
÷
÷
ø
ö
ç
ç
è
æ
+ ba
b
ba
a
Ýòî çíà÷èò, ÷òî
ÀËÃÅÁÐÀ
§ 10. Ïðåîáðàçîâàíèå òðèãîíîì. âûðàæåíèé
ÀËÃÅÁÐÀ
Ðàçäåë II. ÂÛÐÀÆÅÍÈß
119
118
òî÷êà ñ êîîðäèíàòàìè
22
ba
a
+
è
22
ba
b
+
ëåæèò
íà åäèíè÷íîé îêðóæíîñòè, ïîýòîìó ñóùåñòâóåò òà-
êîå
,
a
÷òî
.cos,sin
2222
a=
+
a=
+ ba
b
ba
a
Îáîçíà÷èâ
22
ba +
÷åðåç À, èìååì
).sincoscos(sinsincos ttAtbta a+a=+
Ïðèìåíèâ ê âûðàæåíèþ â ñêîáêàõ ôîðìóëó (3) èç
ï. 79, ïîëó÷èì
).(sinsincos a+=+ tAtbta
×èñëà a,,, Aba ñâÿçàíû äðóã ñ äðóãîì ñîîòíîøå-
íèÿìè
,,cos,sin
22
baAAbAa +=a=a=
.cos,sin
2222
ba
b
ba
a
+
=a
+
=a
Íàïðèìåð,
),2sin(52cos42sin3 a+=+ ttt
ãäå
.
5
3
cos,
5
4
sin =a=a
88. Ïðåîáðàçîâàíèå âûðàæåíèé, ñîäåðæàùèõ
îáðàòíûå òðèãîíîìåòðè÷åñêèå ôóíêöèè. Äëÿ ïðå-
îáðàçîâàíèÿ âûðàæåíèé, ñîäåðæàùèõ îáðàòíûå
òðèãîíîìåòðè÷åñêèå ôóíêöèè, èñïîëüçóþò îïðåäåëå-
íèÿ ýòèõ ôóíêöèé (ñì. ïï. 126128) è ôîðìóëû òðè-
ãîíîìåòðèè.
Ï ð è ì å ð 1. Óïðîñòèòü âûðàæåíèå
),(arccossin x
ãäå
.11 ££- x
q Ïîëîæèì
.arccos
xy =
Òîãäà
,cos
xy =
ãäå
.0 p££ y
Íóæíî íàéòè
.sin y
Èçâåñòíî, ÷òî
=y
2
sin
,cos1
2
y-=
ïîýòîìó
.1sin
22
xy -=
Íî
,0 p££ y
à
íà îòðåçêå
],0[ p
ñèíóñ ïðèíèìàåò òîëüêî íåîòðèöà-
òåëüíûå çíà÷åíèÿ. Òàêèì îáðàçîì,
,1sin
2
xy -=
ò. å.
.1)(arccossin
2
xx -=
n
Ï ð è ì å ð 2. Âû÷èñëèòü
)).6,0(arccos5,0(tg -
q Ïóñòü
).6,0(arccos -=a
Òîãäà
,6,0cos -=a
ãäå
.2/ p<a<p
Íóæíî âû÷èñëèòü
).2/(tg a
Èìååì (ñì.
ï. 83)
.2,0)6,01(5,0)cos1(5,0)2/(cos
2
=-=a+=a
Äàëåå, òàê êàê
)2/(cos
1
)2/(tg1
2
2
a
=a+
(ñì. ï. 81),
òî
,5)2/(tg1
2
=a+
îòêóäà
,4)2/(tg
2
=a
ò. å.
tg (a / 2) = 2 èëè
.2)2/(tg -=a
Ïî óñëîâèþ,
,2/ p<a<p
ò. å.
,2/2/4/ p<a<p
à â èíòåðâàëå
)2/,4/( pp
èìååì
.0)2/(tg >a
Èòàê,
,2)2/(tg =a
ò. å.
.2))6,0(arccos5,0(tg =-
n
ÀËÃÅÁÐÀ
§ 10. Ïðåîáðàçîâàíèå òðèãîíîì. âûðàæåíèé
ÀËÃÅÁÐÀ
Ðàçäåë II. ÂÛÐÀÆÅÍÈß
119
118
òî÷êà ñ êîîðäèíàòàìè
22
ba
a
+
è
22
ba
b
+
ëåæèò
íà åäèíè÷íîé îêðóæíîñòè, ïîýòîìó ñóùåñòâóåò òà-
êîå
,
a
÷òî
.cos,sin
2222
a=
+
a=
+ ba
b
ba
a
Îáîçíà÷èâ
22
ba +
÷åðåç À, èìååì
).sincoscos(sinsincos ttAtbta a+a=+
Ïðèìåíèâ ê âûðàæåíèþ â ñêîáêàõ ôîðìóëó (3) èç
ï. 79, ïîëó÷èì
).(sinsincos a+=+ tAtbta
×èñëà a,,, Aba ñâÿçàíû äðóã ñ äðóãîì ñîîòíîøå-
íèÿìè
,,cos,sin
22
baAAbAa +=a=a=
.cos,sin
2222
ba
b
ba
a
+
=a
+
=a
Íàïðèìåð,
),2sin(52cos42sin3 a+=+ ttt
ãäå
.
5
3
cos,
5
4
sin =a=a
88. Ïðåîáðàçîâàíèå âûðàæåíèé, ñîäåðæàùèõ
îáðàòíûå òðèãîíîìåòðè÷åñêèå ôóíêöèè. Äëÿ ïðå-
îáðàçîâàíèÿ âûðàæåíèé, ñîäåðæàùèõ îáðàòíûå
òðèãîíîìåòðè÷åñêèå ôóíêöèè, èñïîëüçóþò îïðåäåëå-
íèÿ ýòèõ ôóíêöèé (ñì. ïï. 126128) è ôîðìóëû òðè-
ãîíîìåòðèè.
Ï ð è ì å ð 1. Óïðîñòèòü âûðàæåíèå
),(arccossin x
ãäå
.11 ££- x
q Ïîëîæèì
.arccos
xy =
Òîãäà
,cos
xy =
ãäå
.0 p££ y
Íóæíî íàéòè
.sin y
Èçâåñòíî, ÷òî
=y
2
sin
,cos1
2
y-=
ïîýòîìó
.1sin
22
xy -=
Íî
,0 p££ y
à
íà îòðåçêå
],0[ p
ñèíóñ ïðèíèìàåò òîëüêî íåîòðèöà-
òåëüíûå çíà÷åíèÿ. Òàêèì îáðàçîì,
,1sin
2
xy -=
ò. å.
.1)(arccossin
2
xx -=
n
Ï ð è ì å ð 2. Âû÷èñëèòü
)).6,0(arccos5,0(tg -
q Ïóñòü
).6,0(arccos -=a
Òîãäà
,6,0cos -=a
ãäå
.2/ p<a<p
Íóæíî âû÷èñëèòü
).2/(tg a
Èìååì (ñì.
ï. 83)
.2,0)6,01(5,0)cos1(5,0)2/(cos
2
=-=a+=a
Äàëåå, òàê êàê
)2/(cos
1
)2/(tg1
2
2
a
=a+
(ñì. ï. 81),
òî
,5)2/(tg1
2
=a+
îòêóäà
,4)2/(tg
2
=a
ò. å.
tg (a / 2) = 2 èëè
.2)2/(tg -=a
Ïî óñëîâèþ,
,2/ p<a<p
ò. å.
,2/2/4/ p<a<p
à â èíòåðâàëå
)2/,4/( pp
èìååì
.0)2/(tg >a
Èòàê,
,2)2/(tg =a
ò. å.
.2))6,0(arccos5,0(tg =-
n
120
ÀËÃÅÁÐÀ
§ 11. Ñâîéñòâà ôóíêöèé
121
,11)1(
2
==f
,42)2(
2
==f
29,53,2)3,2(
2
==f
è ò. ä.
Çàïèñü f(4) â ýòîì ñëó÷àå ëèøåíà ñìûñëà, òàê êàê
÷èñëî 4 íå ïðèíàäëåæèò îòðåçêó [1, 3]. Îòðåçîê
[1, 3] îáëàñòü îïðåäåëåíèÿ ôóíêöèè.
90. Àíàëèòè÷åñêîå çàäàíèå ôóíêöèè. ×òîáû çà-
äàòü ôóíêöèþ, íóæíî óêàçàòü ñïîñîá, ïîçâîëÿþùèé
äëÿ êàæäîãî çíà÷åíèÿ àðãóìåíòà íàéòè ñîîòâåòñòâó-
þùåå çíà÷åíèå ôóíêöèè. Íàèáîëåå óïîòðåáèòåëü-
íûì ÿâëÿåòñÿ ñïîñîá çàäàíèÿ ôóíêöèè ñ ïîìîùüþ
ôîðìóëû y=f(x), ãäå f(x) íåêîòîðîå âûðàæåíèå ñ
ïåðåìåííîé x.  òàêîì ñëó÷àå ãîâîðÿò, ÷òî ôóíêöèÿ
çàäàíà ôîðìóëîé èëè ÷òî ôóíêöèÿ çàäàíà àíàëè-
òè÷åñêè.
Ïóñòü, íàïðèìåð,
,15
2
-+= xxy
ãäå
.0³x
Îá-
ëàñòü îïðåäåëåíèÿ ýòîé ôóíêöèè ëó÷
).,0[ ¥+
×òîáû íàéòè çíà÷åíèå ôóíêöèè â ëþáîé òî÷êå
,0³x
äîñòàòî÷íî íàéòè ÷èñëîâîå çíà÷åíèå âûðàæåíèÿ
15
2
-+ xx
â âûáðàííîé òî÷êå.
Äëÿ àíàëèòè÷åñêè çàäàííîé ôóíêöèè èíîãäà íå
óêàçûâàþò ÿâíî îáëàñòü îïðåäåëåíèÿ ôóíêöèè. Â
òàêîì ñëó÷àå ïîäðàçóìåâàþò, ÷òî îáëàñòü îïðåäåëå-
íèÿ ôóíêöèè
)(xfy =
ñîâïàäàåò ñ îáëàñòüþ îïðåäå-
ëåíèÿ âûðàæåíèÿ
),(xf
ò.å. ñ ìíîæåñòâîì òåõ çíà÷å-
íèé x, ïðè êîòîðûõ âûðàæåíèå
)(xf
èìååò ñìûñë.
Ï ð è ì å ð. Íàéòè îáëàñòü îïðåäåëåíèÿ ôóíê-
öèè: à)
;
2
1
+
=
x
y
á)
.1-= xy
Ðàçäåë III
ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
§ 11. Ñâîéñòâà ôóíêöèé
89. Îïðåäåëåíèå ôóíêöèè. ×èñëîâîé ôóíêöèåé
ñ îáëàñòüþ îïðåäåëåíèÿ D íàçûâàþò ñîîòâåòñòâèå, ïðè
êîòîðîì êàæäîìó ÷èñëó x èç ìíîæåñòâà D ñîïîñòàâ-
ëÿåòñÿ ïî íåêîòîðîìó ïðàâèëó ÷èñëî y, çàâèñÿùåå îò
x. Ïåðåìåííóþ x íàçûâàþò íåçàâèñèìîé ïåðåìåí-
íîé (èëè àðãóìåíòîì). ×èñëî y, ñîîòâåòñòâóþùåå
÷èñëó x, íàçûâàþò çíà÷åíèåì ôóíêöèè f â òî÷êå x
è îáîçíà÷àþò f (x) (÷èòàþò: «ýô îò èêñ»). Áóêâîé f
îáîçíà÷àåòñÿ çàäàííàÿ ôóíêöèÿ, ò.å. ôóíêöèîíàëüíàÿ
çàâèñèìîñòü ìåæäó ïåðåìåííûìè x è y, è èñïîëüçó-
åòñÿ çàïèñü y = f (x). Ãîâîðÿò òàêæå, ÷òî f (x) åñòü
çíà÷åíèå ôóíêöèè f â òî÷êå x.
Âñå çíà÷åíèÿ, êîòîðûå ïðèíèìàåò íåçàâèñèìàÿ
ïåðåìåííàÿ, îáðàçóþò îáëàñòü îïðåäåëåíèÿ ôóíê-
öèè, åå îáîçíà÷àþò D (f).
Âñå çíà÷åíèÿ, êîòîðûå ïðèíèìàåò ôóíêöèÿ f (x) (ïðè
x, ïðèíàäëåæàùèõ îáëàñòè åå îïðåäåëåíèÿ), îáðàçóþò
ìíîæåñòâî çíà÷åíèé ôóíêöèè, åãî îáîçíà÷àþò E (f).
Èìåþòñÿ è äðóãèå ïîäõîäû ê ââåäåíèþ ïîíÿòèÿ
ôóíêöèè, íàïðèìåð òàêîé: ïåðåìåííàÿ y íàçûâàåòñÿ
ôóíêöèåé ïåðåìåííîé x, åñëè çàäàíà òàêàÿ çàâèñèìîñòü
ìåæäó ýòèìè ïåðåìåííûìè, êîòîðàÿ ïîçâîëÿåò äëÿ êàæ-
äîãî çíà÷åíèÿ x îäíîçíà÷íî îïðåäåëèòü çíà÷åíèå y.
Ðàññìîòðèì ôóíêöèþ
,
2
xy =
ãäå
.31 ££ x
Ýòà çàïèñü îçíà÷àåò, ÷òî çàäàíà ñëåäóþùàÿ ôóí-
êöèÿ: êàæäîìó ÷èñëó x èç îòðåçêà [1, 3] ñòàâèòñÿ â
ñîîòâåòñòâèå êâàäðàò ýòîãî ÷èñëà. Íàïðèìåð,

120
ÀËÃÅÁÐÀ
§ 11. Ñâîéñòâà ôóíêöèé
121
,11)1(
2
==f
,42)2(
2
==f
29,53,2)3,2(
2
==f
è ò. ä.
Çàïèñü f(4) â ýòîì ñëó÷àå ëèøåíà ñìûñëà, òàê êàê
÷èñëî 4 íå ïðèíàäëåæèò îòðåçêó [1, 3]. Îòðåçîê
[1, 3] îáëàñòü îïðåäåëåíèÿ ôóíêöèè.
90. Àíàëèòè÷åñêîå çàäàíèå ôóíêöèè. ×òîáû çà-
äàòü ôóíêöèþ, íóæíî óêàçàòü ñïîñîá, ïîçâîëÿþùèé
äëÿ êàæäîãî çíà÷åíèÿ àðãóìåíòà íàéòè ñîîòâåòñòâó-
þùåå çíà÷åíèå ôóíêöèè. Íàèáîëåå óïîòðåáèòåëü-
íûì ÿâëÿåòñÿ ñïîñîá çàäàíèÿ ôóíêöèè ñ ïîìîùüþ
ôîðìóëû y=f(x), ãäå f(x) íåêîòîðîå âûðàæåíèå ñ
ïåðåìåííîé x.  òàêîì ñëó÷àå ãîâîðÿò, ÷òî ôóíêöèÿ
çàäàíà ôîðìóëîé èëè ÷òî ôóíêöèÿ çàäàíà àíàëè-
òè÷åñêè.
Ïóñòü, íàïðèìåð,
,15
2
-+= xxy
ãäå
.0³x
Îá-
ëàñòü îïðåäåëåíèÿ ýòîé ôóíêöèè ëó÷
).,0[ ¥+
×òîáû íàéòè çíà÷åíèå ôóíêöèè â ëþáîé òî÷êå
,0³x
äîñòàòî÷íî íàéòè ÷èñëîâîå çíà÷åíèå âûðàæåíèÿ
15
2
-+ xx
â âûáðàííîé òî÷êå.
Äëÿ àíàëèòè÷åñêè çàäàííîé ôóíêöèè èíîãäà íå
óêàçûâàþò ÿâíî îáëàñòü îïðåäåëåíèÿ ôóíêöèè. Â
òàêîì ñëó÷àå ïîäðàçóìåâàþò, ÷òî îáëàñòü îïðåäåëå-
íèÿ ôóíêöèè
)(xfy =
ñîâïàäàåò ñ îáëàñòüþ îïðåäå-
ëåíèÿ âûðàæåíèÿ
),(xf
ò.å. ñ ìíîæåñòâîì òåõ çíà÷å-
íèé x, ïðè êîòîðûõ âûðàæåíèå
)(xf
èìååò ñìûñë.
Ï ð è ì å ð. Íàéòè îáëàñòü îïðåäåëåíèÿ ôóíê-
öèè: à)
;
2
1
+
=
x
y
á)
.1-= xy
Ðàçäåë III
ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
§ 11. Ñâîéñòâà ôóíêöèé
89. Îïðåäåëåíèå ôóíêöèè. ×èñëîâîé ôóíêöèåé
ñ îáëàñòüþ îïðåäåëåíèÿ D íàçûâàþò ñîîòâåòñòâèå, ïðè
êîòîðîì êàæäîìó ÷èñëó x èç ìíîæåñòâà D ñîïîñòàâ-
ëÿåòñÿ ïî íåêîòîðîìó ïðàâèëó ÷èñëî y, çàâèñÿùåå îò
x. Ïåðåìåííóþ x íàçûâàþò íåçàâèñèìîé ïåðåìåí-
íîé (èëè àðãóìåíòîì). ×èñëî y, ñîîòâåòñòâóþùåå
÷èñëó x, íàçûâàþò çíà÷åíèåì ôóíêöèè f â òî÷êå x
è îáîçíà÷àþò f (x) (÷èòàþò: «ýô îò èêñ»). Áóêâîé f
îáîçíà÷àåòñÿ çàäàííàÿ ôóíêöèÿ, ò.å. ôóíêöèîíàëüíàÿ
çàâèñèìîñòü ìåæäó ïåðåìåííûìè x è y, è èñïîëüçó-
åòñÿ çàïèñü y = f (x). Ãîâîðÿò òàêæå, ÷òî f (x) åñòü
çíà÷åíèå ôóíêöèè f â òî÷êå x.
Âñå çíà÷åíèÿ, êîòîðûå ïðèíèìàåò íåçàâèñèìàÿ
ïåðåìåííàÿ, îáðàçóþò îáëàñòü îïðåäåëåíèÿ ôóíê-
öèè, åå îáîçíà÷àþò D (f).
Âñå çíà÷åíèÿ, êîòîðûå ïðèíèìàåò ôóíêöèÿ f (x) (ïðè
x, ïðèíàäëåæàùèõ îáëàñòè åå îïðåäåëåíèÿ), îáðàçóþò
ìíîæåñòâî çíà÷åíèé ôóíêöèè, åãî îáîçíà÷àþò E (f).
Èìåþòñÿ è äðóãèå ïîäõîäû ê ââåäåíèþ ïîíÿòèÿ
ôóíêöèè, íàïðèìåð òàêîé: ïåðåìåííàÿ y íàçûâàåòñÿ
ôóíêöèåé ïåðåìåííîé x, åñëè çàäàíà òàêàÿ çàâèñèìîñòü
ìåæäó ýòèìè ïåðåìåííûìè, êîòîðàÿ ïîçâîëÿåò äëÿ êàæ-
äîãî çíà÷åíèÿ x îäíîçíà÷íî îïðåäåëèòü çíà÷åíèå y.
Ðàññìîòðèì ôóíêöèþ
,
2
xy =
ãäå
.31 ££ x
Ýòà çàïèñü îçíà÷àåò, ÷òî çàäàíà ñëåäóþùàÿ ôóí-
êöèÿ: êàæäîìó ÷èñëó x èç îòðåçêà [1, 3] ñòàâèòñÿ â
ñîîòâåòñòâèå êâàäðàò ýòîãî ÷èñëà. Íàïðèìåð,
ÀËÃÅÁÐÀ
§ 11. Ñâîéñòâà ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
123122
(ñì.ï.22); îòìåòèâ íà êîîðäèíàòíîé ïëîñêîñòè âñå
òî÷êè ñ àáñöèññîé x = a, ïîëó÷èì ïðÿìóþ, ïàðàëëåëü-
íóþ îñè Oy (ðèñ. 12); ãîâîðÿò, ÷òî x = a óðàâíåíèå
ýòîé ïðÿìîé, â ÷àñòíîñòè, x = 0 óðàâíåíèå ñàìîé
îñè Oy. Àíàëîãè÷íî, îòìåòèâ íà êîîðäèíàòíîé ïëîñ-
êîñòè âñå òî÷êè ñ îðäèíàòîé y = b, ïîëó÷èì ïðÿìóþ,
ïàðàëëåëüíóþ îñè Ox (ðèñ. 12); ãîâîðÿò, ÷òî y = b
óðàâíåíèå ýòîé ïðÿìîé, â ÷àñòíîñòè, y = 0 óðàâíå-
íèå ñàìîé îñè Ox.
Ïîäìíîæåñòâî F òî÷åê êîîðäèíàòíîé ïëîñêîñòè
ÿâëÿåòñÿ ãðàôèêîì íåêîòîðîé ôóíêöèè, åñëè îíî
èìååò íå áîëåå îäíîé îáùåé òî÷êè ñ ëþáîé ïðÿìîé,
ïàðàëëåëüíîé îñè Oy. Òàê, íà ðèñ.13, à èçîáðàæåíî
ïîäìíîæåñòâî, ÿâëÿþùååñÿ ãðàôèêîì íåêîòîðîé ôóí-
êöèè, à íà ðèñ. 13, á ïîäìíîæåñòâî, íå ÿâëÿþùååñÿ
ãðàôèêîì íèêàêîé ôóíêöèè.
Åñëè äàíî ïîäìíîæåñòâî F, ÿâëÿþùååñÿ ãðàôè-
êîì íåêîòîðîé ôóíêöèè, òî ãîâîðÿò, ÷òî ôóíêöèÿ
çàäàíà ãðàôè÷åñêè. Îáëàñòüþ îïðåäåëåíèÿ òàêîé
ôóíêöèè ÿâëÿåòñÿ ïðîåêöèÿ D ìíîæåñòâà F íà îñü
Ox. Åñëè âçÿòü òî÷êó
,Dx Î
òî, ÷òîáû íàéòè ñîîò-
q a) Âûðàæåíèå
2
1
+x
îïðåäåëåíî ïðè âñåõ x,
êðîìå òîãî çíà÷åíèÿ, êîòîðîå îáðàùàåò çíàìåíàòåëü
â íóëü, ò.å. çíà÷åíèÿ x = 2. Ïîýòîìó îáëàñòü îïðåäå-
ëåíèÿ ôóíêöèè ñîñòîèò èç âñåõ ÷èñåë, êðîìå x = 2.
á) Âûðàæåíèå
1-x
îïðåäåëåíî ïðè òåõ x, ïðè
êîòîðûõ
,01 ³-x
ò.å. ïðè
.1³x
Çíà÷èò, îáëàñòü îï-
ðåäåëåíèÿ ôóíêöèè ëó÷
).,1[ ¥+
n
Èíîãäà ôóíêöèÿ çàäàåòñÿ íà ðàçëè÷íûõ ïðîìå-
æóòêàõ ðàçëè÷íûìè ôîðìóëàìè, íàïðèìåð:
î
í
ì
££+
££-+
=
.10,2
,01,32
)
(
xx
xx
xf
åñëè
åñëè
Ýòà ôóíêöèÿ îïðåäåëåíà íà îòðåçêå [1, 1]. Äëÿ
âû÷èñëåíèÿ çíà÷åíèé ôóíêöèè íóæíî ëèøü òî÷íî
îïðåäåëèòü, êàêîé ôîðìóëîé ñëåäóåò âîñïîëüçîâàòü-
ñÿ äëÿ çàäàííîãî êîíêðåòíîãî çíà÷åíèÿ àðãóìåíòà.
Òàê, åñëè íóæíî âû÷èñëèòü f(0,5), òî âîñïîëüçóåìñÿ
ðàâåíñòâîì f(x)=x+2 è ïîëó÷èì f(0,5)=2,5. Åñëè æå
íóæíî âû÷èñëèòü f(0,5), òî âîñïîëüçóåìñÿ ðàâåí-
ñòâîì f(x)=2x+3 è ïîëó÷èì f(0,5)=2.
91. Òàáëè÷íîå çàäàíèå ôóíêöèè. Íà ïðàêòèêå
÷àñòî èñïîëüçóåòñÿ òàáëè÷íûé ñïîñîá çàäàíèÿ ôóí-
êöèè. Ïðè ýòîì ñïîñîáå ïðèâîäèòñÿ òàáëèöà, óêàçû-
âàþùàÿ çíà÷åíèÿ ôóíêöèè äëÿ èìåþùèõñÿ â òàá-
ëèöå çíà÷åíèé àðãóìåíòà. Ïðèìåðàìè òàáëè÷íîãî çà-
äàíèÿ ôóíêöèè ÿâëÿþòñÿ òàáëèöû êâàäðàòîâ, êóáîâ,
êâàäðàòíûõ êîðíåé è ò.ä.
92. Ãðàôè÷åñêîå çàäàíèå ôóíêöèè. Âîçüìåì ïðÿ-
ìîóãîëüíóþ äåêàðòîâó ñèñòåìó êîîðäèíàò xOy
Ðèñ. 12
á)
a)
Ðèñ. 13

ÀËÃÅÁÐÀ
§ 11. Ñâîéñòâà ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
123122
(ñì.ï.22); îòìåòèâ íà êîîðäèíàòíîé ïëîñêîñòè âñå
òî÷êè ñ àáñöèññîé x = a, ïîëó÷èì ïðÿìóþ, ïàðàëëåëü-
íóþ îñè Oy (ðèñ. 12); ãîâîðÿò, ÷òî x = a óðàâíåíèå
ýòîé ïðÿìîé, â ÷àñòíîñòè, x = 0 óðàâíåíèå ñàìîé
îñè Oy. Àíàëîãè÷íî, îòìåòèâ íà êîîðäèíàòíîé ïëîñ-
êîñòè âñå òî÷êè ñ îðäèíàòîé y = b, ïîëó÷èì ïðÿìóþ,
ïàðàëëåëüíóþ îñè Ox (ðèñ. 12); ãîâîðÿò, ÷òî y = b
óðàâíåíèå ýòîé ïðÿìîé, â ÷àñòíîñòè, y = 0 óðàâíå-
íèå ñàìîé îñè Ox.
Ïîäìíîæåñòâî F òî÷åê êîîðäèíàòíîé ïëîñêîñòè
ÿâëÿåòñÿ ãðàôèêîì íåêîòîðîé ôóíêöèè, åñëè îíî
èìååò íå áîëåå îäíîé îáùåé òî÷êè ñ ëþáîé ïðÿìîé,
ïàðàëëåëüíîé îñè Oy. Òàê, íà ðèñ.13, à èçîáðàæåíî
ïîäìíîæåñòâî, ÿâëÿþùååñÿ ãðàôèêîì íåêîòîðîé ôóí-
êöèè, à íà ðèñ. 13, á ïîäìíîæåñòâî, íå ÿâëÿþùååñÿ
ãðàôèêîì íèêàêîé ôóíêöèè.
Åñëè äàíî ïîäìíîæåñòâî F, ÿâëÿþùååñÿ ãðàôè-
êîì íåêîòîðîé ôóíêöèè, òî ãîâîðÿò, ÷òî ôóíêöèÿ
çàäàíà ãðàôè÷åñêè. Îáëàñòüþ îïðåäåëåíèÿ òàêîé
ôóíêöèè ÿâëÿåòñÿ ïðîåêöèÿ D ìíîæåñòâà F íà îñü
Ox. Åñëè âçÿòü òî÷êó
,Dx Î
òî, ÷òîáû íàéòè ñîîò-
q a) Âûðàæåíèå
2
1
+x
îïðåäåëåíî ïðè âñåõ x,
êðîìå òîãî çíà÷åíèÿ, êîòîðîå îáðàùàåò çíàìåíàòåëü
â íóëü, ò.å. çíà÷åíèÿ x = 2. Ïîýòîìó îáëàñòü îïðåäå-
ëåíèÿ ôóíêöèè ñîñòîèò èç âñåõ ÷èñåë, êðîìå x = 2.
á) Âûðàæåíèå
1-x
îïðåäåëåíî ïðè òåõ x, ïðè
êîòîðûõ
,01 ³-x
ò.å. ïðè
.1³x
Çíà÷èò, îáëàñòü îï-
ðåäåëåíèÿ ôóíêöèè ëó÷
).,1[ ¥+
n
Èíîãäà ôóíêöèÿ çàäàåòñÿ íà ðàçëè÷íûõ ïðîìå-
æóòêàõ ðàçëè÷íûìè ôîðìóëàìè, íàïðèìåð:
î
í
ì
££+
££-+
=
.10,2
,01,32
)
(
xx
xx
xf
åñëè
åñëè
Ýòà ôóíêöèÿ îïðåäåëåíà íà îòðåçêå [1, 1]. Äëÿ
âû÷èñëåíèÿ çíà÷åíèé ôóíêöèè íóæíî ëèøü òî÷íî
îïðåäåëèòü, êàêîé ôîðìóëîé ñëåäóåò âîñïîëüçîâàòü-
ñÿ äëÿ çàäàííîãî êîíêðåòíîãî çíà÷åíèÿ àðãóìåíòà.
Òàê, åñëè íóæíî âû÷èñëèòü f(0,5), òî âîñïîëüçóåìñÿ
ðàâåíñòâîì f(x)=x+2 è ïîëó÷èì f(0,5)=2,5. Åñëè æå
íóæíî âû÷èñëèòü f(0,5), òî âîñïîëüçóåìñÿ ðàâåí-
ñòâîì f(x)=2x+3 è ïîëó÷èì f(0,5)=2.
91. Òàáëè÷íîå çàäàíèå ôóíêöèè. Íà ïðàêòèêå
÷àñòî èñïîëüçóåòñÿ òàáëè÷íûé ñïîñîá çàäàíèÿ ôóí-
êöèè. Ïðè ýòîì ñïîñîáå ïðèâîäèòñÿ òàáëèöà, óêàçû-
âàþùàÿ çíà÷åíèÿ ôóíêöèè äëÿ èìåþùèõñÿ â òàá-
ëèöå çíà÷åíèé àðãóìåíòà. Ïðèìåðàìè òàáëè÷íîãî çà-
äàíèÿ ôóíêöèè ÿâëÿþòñÿ òàáëèöû êâàäðàòîâ, êóáîâ,
êâàäðàòíûõ êîðíåé è ò.ä.
92. Ãðàôè÷åñêîå çàäàíèå ôóíêöèè. Âîçüìåì ïðÿ-
ìîóãîëüíóþ äåêàðòîâó ñèñòåìó êîîðäèíàò xOy
Ðèñ. 12
á)
a)
Ðèñ. 13
ÀËÃÅÁÐÀ
§ 11. Ñâîéñòâà ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
125124
Ñîñòàâèì òàáëèöó íåêîòîðûõ çíà÷åíèé ôóíêöèè:
Îòìåòèì òî÷êè (0; 0); (0,5; 0,25); (0,5; 0,25); (1; 1);
(1; 1); (2; 4); (2; 4) íà êîîðäèíàòíîé ïëîñêîñòè è
ñîåäèíèâ èõ ïëàâíîé ëèíèåé, ïîëó÷èì ãðàôèê (à òî÷-
íåå, ýñêèç ãðàôèêà) ôóíêöèè
2
xy =
(ðèñ. 15). Ýòà
ëèíèÿ íàçûâàåòñÿ ïàðàáîëîé. Âîîáùå, ïàðàáîëîé ÿâ-
ëÿåòñÿ ãðàôèê ëþáîé ôóíêöèè âèäà
,
2
axy =
ãäå
0¹a
(ñì. ï. 131).
94. ×åòíûå è íå÷åòíûå ôóíêöèè. Ôóíêöèÿ
)(xfy =
íàçûâàåòñÿ ÷åòíîé, åñëè äëÿ ëþáîãî x èç
îáëàñòè îïðåäåëåíèÿ ôóíêöèè âûïîëíÿåòñÿ ðàâåí-
ñòâî
).()( xfxf =-
Ôóíêöèÿ
)(xfy =
íàçûâàåòñÿ íå÷åòíîé, åñëè äëÿ
ëþáîãî x èç îáëàñòè îïðåäåëåíèÿ ôóíêöèè âûïîëíÿ-
åòñÿ ðàâåíñòâî
).()( xfxf -=-
Íàïðèìåð,
642
,,
xyxyxy ===
÷åòíûå, à
,
3
xy =
,
5
xy =
7
xy =
íå÷åòíûå ôóíêöèè.
Åñëè ôóíêöèÿ
)(xfy =
òàêîâà, ÷òî õîòÿ áû äëÿ
îäíîé ïàðû çíà÷åíèé x è x îêàçàëîñü, ÷òî
),()( xfxf ¹-
è õîòÿ áû äëÿ îäíîé ïàðû çíà÷åíèé x è
x îêàçàëîñü, ÷òî
),()( xfxf -¹-
òî ôóíêöèÿ íå ÿâëÿ-
åòñÿ íè ÷åòíîé, íè íå÷åòíîé.
x
y
1
11
0
0
2
4
4
2
1 0,5
0,5
0,25
0,25
âåòñòâóþùåå âûáðàííîìó çíà÷åíèþ x çíà÷åíèå
ôóíêöèè, íóæíî ÷åðåç òî÷êó x ïðîâåñòè ïðÿìóþ,
ïàðàëëåëüíóþ îñè Oy, äî ïåðåñå÷åíèÿ ñ ãðàôèêîì
F â òî÷êå M. Îðäèíàòà òî÷êè M è åñòü çíà÷åíèå
ôóíêöèè â òî÷êå x.
93. Ãðàôèê ôóíêöèè, çàäàííîé àíàëèòè÷åñêè.
Ïóñòü ôóíêöèÿ çàäàíà àíàëèòè÷åñêè ôîðìóëîé
).(xfy =
Òîãäà åå ãðàôèêîì íàçûâàåòñÿ ìíîæå-
ñòâî âñåõ òî÷åê (x; y) êîîðäèíàòíîé ïëîñêîñòè, ãäå
),(xfy =
à x «ïðîáåãàåò» âñþ îáëàñòü îïðåäåëåíèÿ
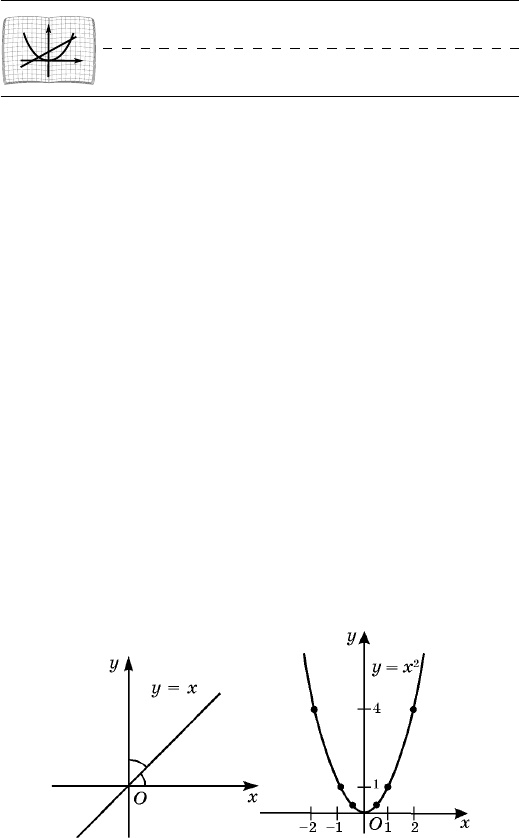
ôóíêöèè f. Íàïðèìåð, ãðàôèêîì ôóíêöèè y = x
ÿâëÿåòñÿ ìíîæåñòâî òî÷åê âèäà (x; x), ò.å. òî÷åê, èìå-
þùèõ îäèíàêîâûå êîîðäèíàòû. Ýòî ìíîæåñòâî òî-
÷åê åñòü áèññåêòðèñà I è III êîîðäèíàòíûõ óãëîâ
(ðèñ. 14).
Ïîñòðîèì òåïåðü ãðàôèê ôóíêöèè
.
2
xy =
Ðèñ. 14 Ðèñ. 15
ÀËÃÅÁÐÀ
§ 11. Ñâîéñòâà ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
125124
Ñîñòàâèì òàáëèöó íåêîòîðûõ çíà÷åíèé ôóíêöèè:
Îòìåòèì òî÷êè (0; 0); (0,5; 0,25); (0,5; 0,25); (1; 1);
(1; 1); (2; 4); (2; 4) íà êîîðäèíàòíîé ïëîñêîñòè è
ñîåäèíèâ èõ ïëàâíîé ëèíèåé, ïîëó÷èì ãðàôèê (à òî÷-
íåå, ýñêèç ãðàôèêà) ôóíêöèè
2
xy =
(ðèñ. 15). Ýòà
ëèíèÿ íàçûâàåòñÿ ïàðàáîëîé. Âîîáùå, ïàðàáîëîé ÿâ-
ëÿåòñÿ ãðàôèê ëþáîé ôóíêöèè âèäà
,
2
axy =
ãäå
0¹a
(ñì. ï. 131).
94. ×åòíûå è íå÷åòíûå ôóíêöèè. Ôóíêöèÿ
)(xfy =
íàçûâàåòñÿ ÷åòíîé, åñëè äëÿ ëþáîãî x èç
îáëàñòè îïðåäåëåíèÿ ôóíêöèè âûïîëíÿåòñÿ ðàâåí-
ñòâî
).()( xfxf =-
Ôóíêöèÿ
)(xfy =
íàçûâàåòñÿ íå÷åòíîé, åñëè äëÿ
ëþáîãî x èç îáëàñòè îïðåäåëåíèÿ ôóíêöèè âûïîëíÿ-
åòñÿ ðàâåíñòâî
).()( xfxf -=-
Íàïðèìåð,
642
,,
xyxyxy ===
÷åòíûå, à
,
3
xy =
,
5
xy =
7
xy =
íå÷åòíûå ôóíêöèè.
Åñëè ôóíêöèÿ
)(xfy =
òàêîâà, ÷òî õîòÿ áû äëÿ
îäíîé ïàðû çíà÷åíèé x è x îêàçàëîñü, ÷òî
),()( xfxf ¹-
è õîòÿ áû äëÿ îäíîé ïàðû çíà÷åíèé x è
x îêàçàëîñü, ÷òî
),()( xfxf -¹-
òî ôóíêöèÿ íå ÿâëÿ-
åòñÿ íè ÷åòíîé, íè íå÷åòíîé.
x
y
1
11
0
0
2
4
4
2
1 0,5
0,5
0,25
0,25
âåòñòâóþùåå âûáðàííîìó çíà÷åíèþ x çíà÷åíèå
ôóíêöèè, íóæíî ÷åðåç òî÷êó x ïðîâåñòè ïðÿìóþ,
ïàðàëëåëüíóþ îñè Oy, äî ïåðåñå÷åíèÿ ñ ãðàôèêîì
F â òî÷êå M. Îðäèíàòà òî÷êè M è åñòü çíà÷åíèå
ôóíêöèè â òî÷êå x.
93. Ãðàôèê ôóíêöèè, çàäàííîé àíàëèòè÷åñêè.
Ïóñòü ôóíêöèÿ çàäàíà àíàëèòè÷åñêè ôîðìóëîé
).(xfy =
Òîãäà åå ãðàôèêîì íàçûâàåòñÿ ìíîæå-
ñòâî âñåõ òî÷åê (x; y) êîîðäèíàòíîé ïëîñêîñòè, ãäå
),(xfy =
à x «ïðîáåãàåò» âñþ îáëàñòü îïðåäåëåíèÿ
ôóíêöèè f. Íàïðèìåð, ãðàôèêîì ôóíêöèè y = x
ÿâëÿåòñÿ ìíîæåñòâî òî÷åê âèäà (x; x), ò.å. òî÷åê, èìå-
þùèõ îäèíàêîâûå êîîðäèíàòû. Ýòî ìíîæåñòâî òî-
÷åê åñòü áèññåêòðèñà I è III êîîðäèíàòíûõ óãëîâ
(ðèñ. 14).
Ïîñòðîèì òåïåðü ãðàôèê ôóíêöèè
.
2
xy =
Ðèñ. 14 Ðèñ. 15
