Маслова Т.Н., Суходский А.М. Справочник школьника по математике. 5-11 кл
Подождите немного. Документ загружается.

ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
137136
1
0
. Îáëàñòü îïðåäåëåíèÿ âñÿ ÷èñëîâàÿ ïðÿìàÿ.
2
0
. Ôóíêöèÿ íå÷åòíàÿ:
).()()(
33
xfxxxf -=-=-=-
3
0
. Ôóíêöèÿ âîçðàñòàåò íà âñåé ÷èñëîâîé ïðÿ-
ìîé.
Ãðàôèê ôóíêöèè
3
xy =
èçîáðàæåí íà ðèñ.27. Îí
íàçûâàåòñÿ êóáè÷åñêîé ïàðàáîëîé.
105. Ñòåïåííàÿ ôóíêöèÿ ñ íàòóðàëüíûì ïîêà-
çàòåëåì. Ôóíêöèÿ
,
n
xy
=
ãäå n íàòóðàëüíîå ÷èñ-
ëî, íàçûâàåòñÿ ñòåïåííîé ôóíêöèåé ñ íàòóðàëü-
íûì ïîêàçàòåëåì. Ïðè n = 1 ïîëó÷àåì ôóíêöèþ
y = x, åå ñâîéñòâà ðàññìîòðåíû â ï. 99, à ãðàôèê (ïðÿ-
ìàÿ) èçîáðàæåí íà ðèñ. 14. Ïðè n = 2 ïîëó÷àåì
ôóíêöèþ
,
2
xy =
åå ñâîéñòâà ðàññìîòðåíû â ï. 103,
à ãðàôèê (ïàðàáîëà) èçîáðàæåí íà ðèñ. 15. Ïðè n =
= 3 ïîëó÷àåì ôóíêöèþ
,
3
xy =
åå ñâîéñòâà ðàñ-
Ãðàôèê îáðàòíîé ïðîïîðöèîíàëüíîñòè
xky /=
íàçûâàþò ãèïåðáîëîé.
103. Ôóíêöèÿ
.xy
2
=
Ïåðå÷èñëèì ñâîéñòâà ôóí-
êöèè
:
2
xy =
1
0
. Îáëàñòü îïðåäåëåíèÿ âñÿ ÷èñëîâàÿ ïðÿìàÿ.
2
0
. Ôóíêöèÿ ÷åòíàÿ:
).()()(
22
xfxxxf ==-=-
3
0
. Íà ïðîìåæóòêå
),0[ ¥+
ôóíêöèÿ âîçðàñòàåò.
4
0
. Íà ïðîìåæóòêå
]0,(-¥
ôóíêöèÿ óáûâàåò.
Ãðàôèêîì ôóíêöèè
2
xy =
ÿâëÿåòñÿ ïàðàáîëà (ñì.
ï. 93). Ýòîò ãðàôèê èçîáðàæåí íà ðèñ. 15.
104. Ôóíêöèÿ
.xy
3
=
Ïåðå÷èñëèì ñâîéñòâà ôóí-
êöèè
3
xy =
:
Ðèñ.25Ðèñ.24
Ðèñ.26 Ðèñ.27
ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
137136
1
0
. Îáëàñòü îïðåäåëåíèÿ âñÿ ÷èñëîâàÿ ïðÿìàÿ.
2
0
. Ôóíêöèÿ íå÷åòíàÿ:
).()()(
33
xfxxxf -=-=-=-
3
0
. Ôóíêöèÿ âîçðàñòàåò íà âñåé ÷èñëîâîé ïðÿ-
ìîé.
Ãðàôèê ôóíêöèè
3
xy =
èçîáðàæåí íà ðèñ.27. Îí
íàçûâàåòñÿ êóáè÷åñêîé ïàðàáîëîé.
105. Ñòåïåííàÿ ôóíêöèÿ ñ íàòóðàëüíûì ïîêà-
çàòåëåì. Ôóíêöèÿ
,
n
xy
=
ãäå n íàòóðàëüíîå ÷èñ-
ëî, íàçûâàåòñÿ ñòåïåííîé ôóíêöèåé ñ íàòóðàëü-
íûì ïîêàçàòåëåì. Ïðè n = 1 ïîëó÷àåì ôóíêöèþ
y = x, åå ñâîéñòâà ðàññìîòðåíû â ï. 99, à ãðàôèê (ïðÿ-
ìàÿ) èçîáðàæåí íà ðèñ. 14. Ïðè n = 2 ïîëó÷àåì
ôóíêöèþ
,
2
xy =
åå ñâîéñòâà ðàññìîòðåíû â ï. 103,
à ãðàôèê (ïàðàáîëà) èçîáðàæåí íà ðèñ. 15. Ïðè n =
= 3 ïîëó÷àåì ôóíêöèþ
,
3
xy =
åå ñâîéñòâà ðàñ-
Ãðàôèê îáðàòíîé ïðîïîðöèîíàëüíîñòè
xky /=
íàçûâàþò ãèïåðáîëîé.
103. Ôóíêöèÿ
.xy
2
=
Ïåðå÷èñëèì ñâîéñòâà ôóí-
êöèè
:
2
xy =
1
0
. Îáëàñòü îïðåäåëåíèÿ âñÿ ÷èñëîâàÿ ïðÿìàÿ.
2
0
. Ôóíêöèÿ ÷åòíàÿ:
).()()(
22
xfxxxf ==-=-
3
0
. Íà ïðîìåæóòêå
),0[ ¥+
ôóíêöèÿ âîçðàñòàåò.
4
0
. Íà ïðîìåæóòêå
]0,(-¥
ôóíêöèÿ óáûâàåò.
Ãðàôèêîì ôóíêöèè
2
xy =
ÿâëÿåòñÿ ïàðàáîëà (ñì.
ï. 93). Ýòîò ãðàôèê èçîáðàæåí íà ðèñ. 15.
104. Ôóíêöèÿ
.xy
3
=
Ïåðå÷èñëèì ñâîéñòâà ôóí-
êöèè
3
xy =
:
Ðèñ.25Ðèñ.24
Ðèñ.26 Ðèñ.27
ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
139138
öèÿ
.
3
xy =
Ãðàôèê òàêîé ôóíêöèè íàïîìèíàåò êó-
áè÷åñêóþ ïàðàáîëó (òîëüêî âåòâè ãðàôèêà òåì êðó-
÷å èäóò ââåðõ è âíèç, ÷åì áîëüøå n; ðèñ. 29). Îòìå-
òèì òàêæå, ÷òî íà ïðîìåæóòêå (0, 1) ãðàôèê ôóíê-
öèè
n
xy
=
òåì ìåäëåííåå îòäàëÿåòñÿ îò îñè Ox ñ
ðîñòîì x, ÷åì áîëüøå n.
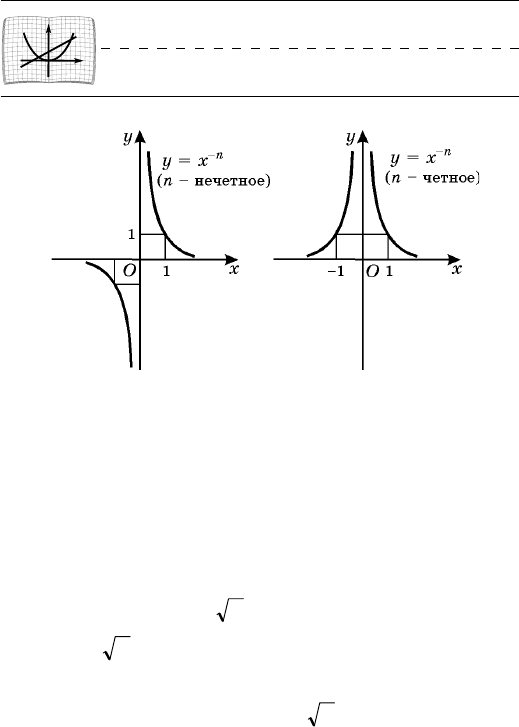
106. Ñòåïåííàÿ ôóíêöèÿ ñ öåëûì îòðèöàòåëüíûì
ïîêàçàòåëåì. Ðàññìîòðèì ôóíêöèþ
,
n
xy
-
=
ãäå
n íàòóðàëüíîå ÷èñëî. Ïðè n = 1 ïîëó÷àåì
1-
= xy
èëè
./1 xy =
Ñâîéñòâà ýòîé ôóíêöèè ðàññìîòðåíû
â ï. 102, à åå ãðàôèê (ãèïåðáîëà) èçîáðàæåí íà ðèñ.
24.
Ïóñòü n íå÷åòíîå ÷èñëî, áîëüøåå åäèíèöû:
n =3, 5, 7, ... .  ýòîì ñëó÷àå ôóíêöèÿ
n
xy
-
=
îáëàäàåò
â îñíîâíîì òåìè æå ñâîéñòâàìè, ÷òî è ôóíêöèÿ
./1 xy =
Ãðàôèê ôóíêöèè
n
xy
-
=
(n =3, 5, 7, ...) íàïî-
ìèíàåò ãðàôèê ôóíêöèè
xy /1=
(ðèñ. 30, à).
Ïóñòü n ÷åòíîå ÷èñëî, íàïðèìåð n = 2. Ïåðå-
÷èñëèì íåêîòîðûå ñâîéñòâà ôóíêöèè
:
2
-
= xy
1
0
. Ôóíêöèÿ îïðåäåëåíà ïðè âñåõ
.0¹x
2
0
. Ôóíêöèÿ ÷åòíàÿ.
3
0
. Ôóíêöèÿ óáûâàåò íà
),0( ¥+
è âîçðàñòàåò íà
).0,(-¥
Òåìè æå ñâîéñòâàìè îáëàäàþò ëþáûå ôóíêöèè
âèäà
n
xy
-
= ïðè ÷åòíîì n, áîëüøåì äâóõ.
ñìîòðåíû â ï. 104, à ãðàôèê (êóáè÷åñêàÿ ïàðàáîëà)
èçîáðàæåí íà ðèñ. 27.
Ïóñòü n ïðîèçâîëüíîå ÷åòíîå íàòóðàëüíîå
÷èñëî, áîëüøåå äâóõ: n = 4, 6, 8, ... .  ýòîì ñëó÷àå
ôóíêöèÿ
n
xy
=
îáëàäàåò òåìè æå ñâîéñòâàìè, ÷òî
è ôóíêöèÿ
.
2
xy =
Ãðàôèê òàêîé ôóíêöèè íàïî-
ìèíàåò ïàðàáîëó
,
2
xy =
òîëüêî âåòâè ãðàôèêà ïðè
1>x
òåì êðó÷å èäóò ââåðõ, ÷åì áîëüøå n, à ïðè
1<x
òåì «òåñíåå ïðèæèìàþòñÿ» ê îñè Ox, ÷åì
áîëüøå n (ðèñ. 28).
Ïóñòü n ïðîèçâîëüíîå íå÷åòíîå ÷èñëî, áîëü-
øåå òðåõ, ò.å. n = 5, 7, 9, ... .  ýòîì ñëó÷àå ôóíêöèÿ
n
xy
=
îáëàäàåò òåìè æå ñâîéñòâàìè, ÷òî è ôóíê-
Ðèñ. 29Ðèñ. 28
ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
139138
öèÿ
.
3
xy =
Ãðàôèê òàêîé ôóíêöèè íàïîìèíàåò êó-
áè÷åñêóþ ïàðàáîëó (òîëüêî âåòâè ãðàôèêà òåì êðó-
÷å èäóò ââåðõ è âíèç, ÷åì áîëüøå n; ðèñ. 29). Îòìå-
òèì òàêæå, ÷òî íà ïðîìåæóòêå (0, 1) ãðàôèê ôóíê-
öèè
n
xy
=
òåì ìåäëåííåå îòäàëÿåòñÿ îò îñè Ox ñ
ðîñòîì x, ÷åì áîëüøå n.
106. Ñòåïåííàÿ ôóíêöèÿ ñ öåëûì îòðèöàòåëüíûì
ïîêàçàòåëåì. Ðàññìîòðèì ôóíêöèþ
,
n
xy
-
=
ãäå
n íàòóðàëüíîå ÷èñëî. Ïðè n = 1 ïîëó÷àåì
1-
= xy
èëè
./1 xy =
Ñâîéñòâà ýòîé ôóíêöèè ðàññìîòðåíû
â ï. 102, à åå ãðàôèê (ãèïåðáîëà) èçîáðàæåí íà ðèñ.
24.
Ïóñòü n íå÷åòíîå ÷èñëî, áîëüøåå åäèíèöû:
n =3, 5, 7, ... .  ýòîì ñëó÷àå ôóíêöèÿ
n
xy
-
=
îáëàäàåò
â îñíîâíîì òåìè æå ñâîéñòâàìè, ÷òî è ôóíêöèÿ
./1 xy =
Ãðàôèê ôóíêöèè
n
xy
-
=
(n =3, 5, 7, ...) íàïî-
ìèíàåò ãðàôèê ôóíêöèè
xy /1=
(ðèñ. 30, à).
Ïóñòü n ÷åòíîå ÷èñëî, íàïðèìåð n = 2. Ïåðå-
÷èñëèì íåêîòîðûå ñâîéñòâà ôóíêöèè
:
2
-
= xy
1
0
. Ôóíêöèÿ îïðåäåëåíà ïðè âñåõ
.0¹x
2
0
. Ôóíêöèÿ ÷åòíàÿ.
3
0
. Ôóíêöèÿ óáûâàåò íà
),0( ¥+
è âîçðàñòàåò íà
).0,(-¥
Òåìè æå ñâîéñòâàìè îáëàäàþò ëþáûå ôóíêöèè
âèäà
n
xy
-
= ïðè ÷åòíîì n, áîëüøåì äâóõ.
ñìîòðåíû â ï. 104, à ãðàôèê (êóáè÷åñêàÿ ïàðàáîëà)
èçîáðàæåí íà ðèñ. 27.
Ïóñòü n ïðîèçâîëüíîå ÷åòíîå íàòóðàëüíîå
÷èñëî, áîëüøåå äâóõ: n = 4, 6, 8, ... .  ýòîì ñëó÷àå
ôóíêöèÿ
n
xy
=
îáëàäàåò òåìè æå ñâîéñòâàìè, ÷òî
è ôóíêöèÿ
.
2
xy =
Ãðàôèê òàêîé ôóíêöèè íàïî-
ìèíàåò ïàðàáîëó
,
2
xy =
òîëüêî âåòâè ãðàôèêà ïðè
1>x
òåì êðó÷å èäóò ââåðõ, ÷åì áîëüøå n, à ïðè
1<x
òåì «òåñíåå ïðèæèìàþòñÿ» ê îñè Ox, ÷åì
áîëüøå n (ðèñ. 28).
Ïóñòü n ïðîèçâîëüíîå íå÷åòíîå ÷èñëî, áîëü-
øåå òðåõ, ò.å. n = 5, 7, 9, ... .  ýòîì ñëó÷àå ôóíêöèÿ
n
xy
=
îáëàäàåò òåìè æå ñâîéñòâàìè, ÷òî è ôóíê-
Ðèñ. 29Ðèñ. 28
ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
141140
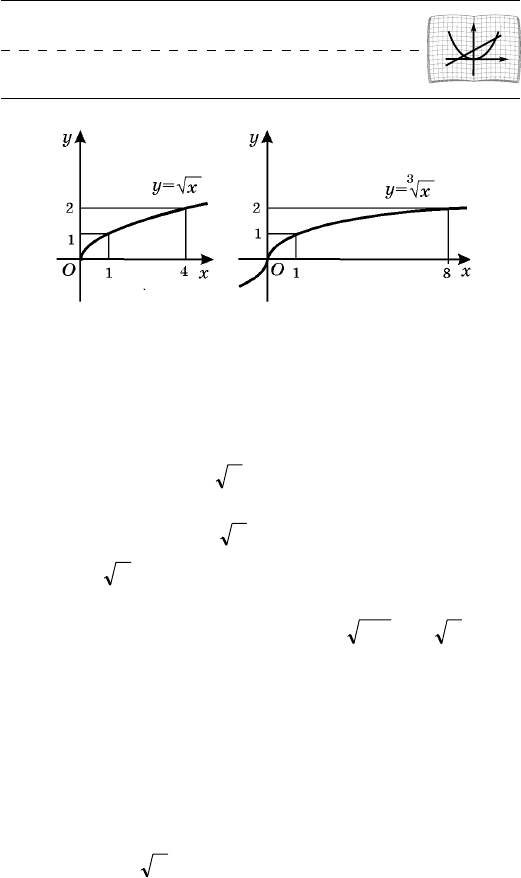
Íàíåñåì ïîëó÷åííûå òî÷êè íà êîîðäèíàòíóþ
ïëîñêîñòü è ñîåäèíèì èõ ïëàâíîé êðèâîé. Ïîëó÷èì
ãðàôèê ôóíêöèè
xy =
(ðèñ. 31, à).
108. Ôóíêöèÿ
.xy
3
=
Ïåðå÷èñëèì ñâîéñòâà ôóí-
êöèè
:
3
xy =
1
0
. Îáëàñòü îïðåäåëåíèÿ âñÿ ÷èñëîâàÿ ïðÿìàÿ.
2
0
. Ôóíêöèÿ íå÷åòíàÿ, òàê êàê
.
33
xx -=-
3
0
. Ôóíêöèÿ âîçðàñòàåò íà âñåé ÷èñëîâîé ïðÿìîé.
Äëÿ ïîñòðîåíèÿ âåòâè ãðàôèêà ïðè
0³x
ñîñòà-
âèì òàáëèöó çíà÷åíèé ôóíêöèè: x = 0, y = 0; x = 1,
y = 1; x = 4, y = 1,6; x = 8, y = 2.
Íàíåñåì ïîëó÷åííûå òî÷êè íà êîîðäèíàòíóþ
ïëîñêîñòü è ñîåäèíèì èõ ïëàâíîé êðèâîé; çàòåì ê
ïîñòðîåííîé âåòâè äîáàâèì âåòâü, ñèììåòðè÷íóþ åé
îòíîñèòåëüíî íà÷àëà êîîðäèíàò. Ïîëó÷èì ãðàôèê
ôóíêöèè
3
xy =
(ðèñ. 31, á).
Ãðàôèê ôóíêöèè y = x
n
ïðè ÷åòíîì n èçîáðà-
æåí íà ðèñ. 30, á.
107. Ôóíêöèÿ
.xy =
Ïåðå÷èñëèì ñâîéñòâà ôóí-
êöèè
:xy =
1
0
. Îáëàñòü îïðåäåëåíèÿ ëó÷
).,0[ ¥+
Ýòî ñëå-
äóåò èç òîãî, ÷òî âûðàæåíèå
x
îïðåäåëåíî ëèøü
ïðè
.0³x
2
0
. Ôóíêöèÿ íè ÷åòíàÿ, íè íå÷åòíàÿ.
3
0
. Ôóíêöèÿ âîçðàñòàåò íà ëó÷å
).,0[ ¥+
Äëÿ ïîñòðîåíèÿ ãðàôèêà ñîñòàâèì òàáëèöó çíà-
÷åíèé ôóíêöèè: x = 0, y = 0; x = 1, y = 1; x = 2, y = 1,4;
x = 4, y = 2; x = 9, y = 3.
á)a)
a)
á)
Ðèñ. 30
Ðèñ. 31
ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
141140
Íàíåñåì ïîëó÷åííûå òî÷êè íà êîîðäèíàòíóþ
ïëîñêîñòü è ñîåäèíèì èõ ïëàâíîé êðèâîé. Ïîëó÷èì
ãðàôèê ôóíêöèè
xy =
(ðèñ. 31, à).
108. Ôóíêöèÿ
.xy
3
=
Ïåðå÷èñëèì ñâîéñòâà ôóí-
êöèè
:
3
xy =
1
0
. Îáëàñòü îïðåäåëåíèÿ âñÿ ÷èñëîâàÿ ïðÿìàÿ.
2
0
. Ôóíêöèÿ íå÷åòíàÿ, òàê êàê
.
33
xx -=-
3
0
. Ôóíêöèÿ âîçðàñòàåò íà âñåé ÷èñëîâîé ïðÿìîé.
Äëÿ ïîñòðîåíèÿ âåòâè ãðàôèêà ïðè
0³x
ñîñòà-
âèì òàáëèöó çíà÷åíèé ôóíêöèè: x = 0, y = 0; x = 1,
y = 1; x = 4, y = 1,6; x = 8, y = 2.
Íàíåñåì ïîëó÷åííûå òî÷êè íà êîîðäèíàòíóþ
ïëîñêîñòü è ñîåäèíèì èõ ïëàâíîé êðèâîé; çàòåì ê
ïîñòðîåííîé âåòâè äîáàâèì âåòâü, ñèììåòðè÷íóþ åé
îòíîñèòåëüíî íà÷àëà êîîðäèíàò. Ïîëó÷èì ãðàôèê
ôóíêöèè
3
xy =
(ðèñ. 31, á).
Ãðàôèê ôóíêöèè y = x
n
ïðè ÷åòíîì n èçîáðà-
æåí íà ðèñ. 30, á.
107. Ôóíêöèÿ
.xy =
Ïåðå÷èñëèì ñâîéñòâà ôóí-
êöèè
:xy =
1
0
. Îáëàñòü îïðåäåëåíèÿ ëó÷
).,0[ ¥+
Ýòî ñëå-
äóåò èç òîãî, ÷òî âûðàæåíèå
x
îïðåäåëåíî ëèøü
ïðè
.0³x
2
0
. Ôóíêöèÿ íè ÷åòíàÿ, íè íå÷åòíàÿ.
3
0
. Ôóíêöèÿ âîçðàñòàåò íà ëó÷å
).,0[ ¥+
Äëÿ ïîñòðîåíèÿ ãðàôèêà ñîñòàâèì òàáëèöó çíà-
÷åíèé ôóíêöèè: x = 0, y = 0; x = 1, y = 1; x = 2, y = 1,4;
x = 4, y = 2; x = 9, y = 3.
á)a)
a)
á)
Ðèñ. 30
Ðèñ. 31
ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
143142
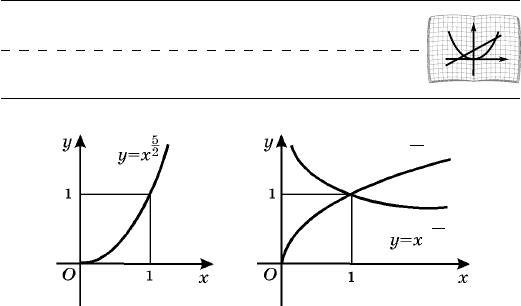
Íà ðèñ. 33 èçîáðàæåí ãðàôèê ôóíêöèè
.
2/5
xy =
Îí çàêëþ÷åí ìåæäó ãðàôèêàìè ôóíêöèé
2
xy =
è
,
3
xy =
çàäàííûõ íà ïðîìåæóòêå
).,0[ ¥+
Ïîäîáíûé
âèä èìååò ãðàôèê ëþáîé ôóíêöèè âèäà
,
r
xy
=
ãäå
.1>r
Íà ðèñ. 34 èçîáðàæåí ãðàôèê ôóíêöèè
.
3/2
xy =
Ïîäîáíûé âèä èìååò ãðàôèê ëþáîé ñòåïåííîé ôóíê-
öèè
,
r
xy
=
ãäå
.10 << r
111. Ñòåïåííàÿ ôóíêöèÿ ñ îòðèöàòåëüíûì äðîá-
íûì ïîêàçàòåëåì. Ðàññìîòðèì ôóíêöèþ
,
r
xy
-
=
ãäå r ïîëîæèòåëüíàÿ íåñîêðàòèìàÿ äðîáü. Ïåðå-
÷èñëèì ñâîéñòâà ýòîé ôóíêöèè:
1
0
. Îáëàñòü îïðåäåëåíèÿ ïðîìåæóòîê
).,0( ¥+
2
0
. Ôóíêöèÿ íè ÷åòíàÿ, íè íå÷åòíàÿ.
3
0
. Ôóíêöèÿ óáûâàåò íà
).,0( ¥+
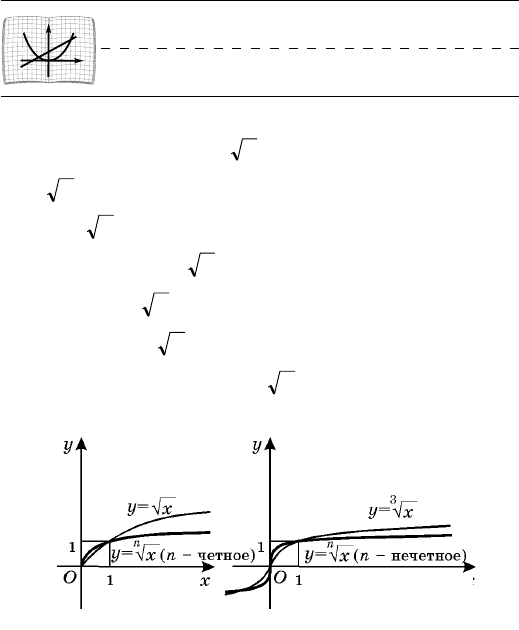
109. Ôóíêöèÿ .xy
n
= Ïðè ÷åòíîì n ôóíêöèÿ
n
xy
=
îáëàäàåò òåìè æå ñâîéñòâàìè, ÷òî è ôóíê-
öèÿ
xy =
(ñì. ï. 107), åå ãðàôèê íàïîìèíàåò ãðà-
ôèê ôóíêöèè
xy =
(ðèñ. 32, à). Ïðè íå÷åòíîì n
ôóíêöèÿ
n
xy
=
îáëàäàåò òåìè æå ñâîéñòâàìè, ÷òî
è ôóíêöèÿ
3
xy =
(ñì. ï. 108), à åå ãðàôèê íàïîìè-
íàåò ãðàôèê ôóíêöèè
3
xy =
(ðèñ. 32, á).
110. Ñòåïåííàÿ ôóíêöèÿ ñ ïîëîæèòåëüíûì äðîá-
íûì ïîêàçàòåëåì. Ðàññìîòðèì ôóíêöèþ
,
r
xy
=
ãäå
r ïîëîæèòåëüíàÿ íåñîêðàòèìàÿ äðîáü. Ïåðå÷èñ-
ëèì íåêîòîðûå ñâîéñòâà ýòîé ôóíêöèè:
1
0
. Îáëàñòü îïðåäåëåíèÿ ëó÷
).,0[ ¥+
2
0
. Ôóíêöèÿ íè ÷åòíàÿ, íè íå÷åòíàÿ.
3
0
. Ôóíêöèÿ âîçðàñòàåò íà
).,0[ ¥+
á)
a)
1
2
y = x
2
3
Ðèñ. 33
Ðèñ. 34
Ðèñ. 32
ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
143142
Íà ðèñ. 33 èçîáðàæåí ãðàôèê ôóíêöèè
.
2/5
xy =
Îí çàêëþ÷åí ìåæäó ãðàôèêàìè ôóíêöèé
2
xy =
è
,
3
xy =
çàäàííûõ íà ïðîìåæóòêå
).,0[ ¥+
Ïîäîáíûé
âèä èìååò ãðàôèê ëþáîé ôóíêöèè âèäà
,
r
xy
=
ãäå
.1>r
Íà ðèñ. 34 èçîáðàæåí ãðàôèê ôóíêöèè
.
3/2
xy =
Ïîäîáíûé âèä èìååò ãðàôèê ëþáîé ñòåïåííîé ôóíê-
öèè
,
r
xy
=
ãäå
.10 << r
111. Ñòåïåííàÿ ôóíêöèÿ ñ îòðèöàòåëüíûì äðîá-
íûì ïîêàçàòåëåì. Ðàññìîòðèì ôóíêöèþ
,
r
xy
-
=
ãäå r ïîëîæèòåëüíàÿ íåñîêðàòèìàÿ äðîáü. Ïåðå-
÷èñëèì ñâîéñòâà ýòîé ôóíêöèè:
1
0
. Îáëàñòü îïðåäåëåíèÿ ïðîìåæóòîê
).,0( ¥+
2
0
. Ôóíêöèÿ íè ÷åòíàÿ, íè íå÷åòíàÿ.
3
0
. Ôóíêöèÿ óáûâàåò íà
).,0( ¥+
109. Ôóíêöèÿ .xy
n
= Ïðè ÷åòíîì n ôóíêöèÿ
n
xy
=
îáëàäàåò òåìè æå ñâîéñòâàìè, ÷òî è ôóíê-
öèÿ
xy =
(ñì. ï. 107), åå ãðàôèê íàïîìèíàåò ãðà-
ôèê ôóíêöèè
xy =
(ðèñ. 32, à). Ïðè íå÷åòíîì n
ôóíêöèÿ
n
xy
=
îáëàäàåò òåìè æå ñâîéñòâàìè, ÷òî
è ôóíêöèÿ
3
xy =
(ñì. ï. 108), à åå ãðàôèê íàïîìè-
íàåò ãðàôèê ôóíêöèè
3
xy =
(ðèñ. 32, á).
110. Ñòåïåííàÿ ôóíêöèÿ ñ ïîëîæèòåëüíûì äðîá-
íûì ïîêàçàòåëåì. Ðàññìîòðèì ôóíêöèþ
,
r
xy
=
ãäå
r ïîëîæèòåëüíàÿ íåñîêðàòèìàÿ äðîáü. Ïåðå÷èñ-
ëèì íåêîòîðûå ñâîéñòâà ýòîé ôóíêöèè:
1
0
. Îáëàñòü îïðåäåëåíèÿ ëó÷
).,0[ ¥+
2
0
. Ôóíêöèÿ íè ÷åòíàÿ, íè íå÷åòíàÿ.
3
0
. Ôóíêöèÿ âîçðàñòàåò íà
).,0[ ¥+
á)
a)
1
2
y = x
2
3
Ðèñ. 33
Ðèñ. 34
Ðèñ. 32

ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
145144
âî âäîëü îñè Îõ, ïîëó÷èì ãðàôèê ôóíêöèè
}{xy =
íà âñåé ÷èñëîâîé ïðÿìîé (ðèñ. 36).
114. Ïîêàçàòåëüíàÿ ôóíêöèÿ. Ïîêàçàòåëüíàÿ
ôóíêöèÿ çàäàåòñÿ ôîðìóëîé
,
x
ay
=
ãäå
0>a
è
.1¹a
Ïåðå÷èñëèì ñâîéñòâà ôóíêöèè
x
ay
=
ïðè
:1>a
1
0
. Îáëàñòü îïðåäåëåíèÿ âñÿ ÷èñëîâàÿ ïðÿìàÿ.
2
0
. Ìíîæåñòâî çíà÷åíèé ëó÷
).,0( ¥+
3
0
. Ôóíêöèÿ íå ÿâëÿåòñÿ íè ÷åòíîé, íè íå÷åòíîé.
Ýòî ñëåäóåò èç òîãî, ÷òî
xx
aa
¹
-
è
.
xx
aa
-¹
-
4
0
. Ôóíêöèÿ âîçðàñòàåò íà âñåé ÷èñëîâîé ïðÿìîé.
5
0
. Îñü Ox ÿâëÿåòñÿ ãîðèçîíòàëüíîé àñèìïòîòîé
ãðàôèêà ïðè
.-¥®x
Ãðàôèê ôóíêöèè
x
ay
=
ïðè
1>a
âûãëÿäèò òàê,
êàê ïîêàçàíî íà ðèñ. 37, à. Íàïðèìåð, íà ðèñ. 37, á
èçîáðàæåí ãðàôèê ôóíêöèè
.2
x
y
=
Íà ðèñ. 34 èçîáðàæåí ãðàôèê ôóíêöèè
.
2/1
-
= xy
Ïîäîáíûé âèä èìååò ãðàôèê ëþáîé ôóí-
êöèè
,
r
xy
=
ãäå r îòðèöàòåëüíàÿ äðîáü.
112. Ôóíêöèÿ
.xy ][=
Ïîñòðîèì ãðàôèê ôóíê-
öèè
][xy =
(ñì. ï. 33). Åñëè
,10 <£ x
òî
;0][ == xy
åñëè
,21 <£ x
òî
;1][ == xy
åñëè
,01 <£- x
òî
1][ -== xy
è ò.ä. Ãðàôèê ôóíêöèè
][xy =
èçîáðà-
æåí íà ðèñ. 35.
113. Ôóíêöèÿ
{x}.y =
Ïîñòðîèì ãðàôèê ôóíê-
öèè
}{xy =
(ñì. ï. 33). Çàìåòèì, ÷òî äëÿ ëþáîãî x
âûïîëíÿåòñÿ äâîéíîå ðàâåíñòâî
}.1{}{}1{ +==- xxx
Ýòî çíà÷èò, ÷òî
}{xy =
ïåðèîäè÷åñêàÿ ôóíêöèÿ ñ
ïåðèîäîì T = 1.
Åñëè
,10 <£ x
òî
,0][ =x
à ïîòîìó
.][}{ xxxx =-=
Ïîñòðîèâ ãðàôèê ôóíêöèè
}{xy =
íà ïðîìåæóòêå
)1,0[
è ïåðåíåñÿ åãî ïàðàëëåëüíî íà
ðàññòîÿíèÿ n (n íàòóðàëüíîå ÷èñëî) âëåâî è âïðà-
á)
a)
Ðèñ. 36
Ðèñ. 37
Ðèñ. 35
ÀËÃÅÁÐÀ
§ 12. Âèäû ôóíêöèé
ÀËÃÅÁÐÀ
Ðàçäåë III. ÔÓÍÊÖÈÈ È ÃÐÀÔÈÊÈ
145144
âî âäîëü îñè Îõ, ïîëó÷èì ãðàôèê ôóíêöèè
}{xy =
íà âñåé ÷èñëîâîé ïðÿìîé (ðèñ. 36).
114. Ïîêàçàòåëüíàÿ ôóíêöèÿ. Ïîêàçàòåëüíàÿ
ôóíêöèÿ çàäàåòñÿ ôîðìóëîé
,
x
ay
=
ãäå
0>a
è
.1¹a
Ïåðå÷èñëèì ñâîéñòâà ôóíêöèè
x
ay
=
ïðè
:1>a
1
0
. Îáëàñòü îïðåäåëåíèÿ âñÿ ÷èñëîâàÿ ïðÿìàÿ.
2
0
. Ìíîæåñòâî çíà÷åíèé ëó÷
).,0( ¥+
3
0
. Ôóíêöèÿ íå ÿâëÿåòñÿ íè ÷åòíîé, íè íå÷åòíîé.
Ýòî ñëåäóåò èç òîãî, ÷òî
xx
aa
¹
-
è
.
xx
aa
-¹
-
4
0
. Ôóíêöèÿ âîçðàñòàåò íà âñåé ÷èñëîâîé ïðÿìîé.
5
0
. Îñü Ox ÿâëÿåòñÿ ãîðèçîíòàëüíîé àñèìïòîòîé
ãðàôèêà ïðè
.-¥®x
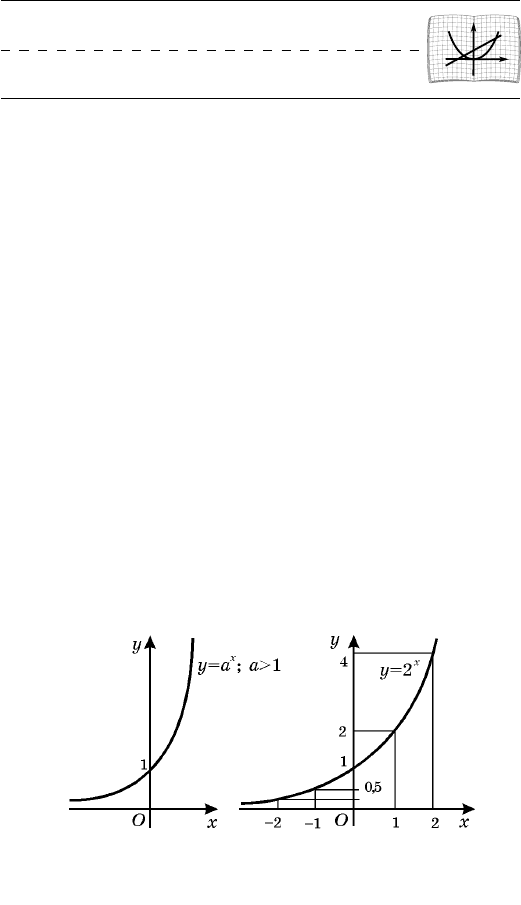
Ãðàôèê ôóíêöèè
x
ay
=
ïðè
1>a
âûãëÿäèò òàê,
êàê ïîêàçàíî íà ðèñ. 37, à. Íàïðèìåð, íà ðèñ. 37, á
èçîáðàæåí ãðàôèê ôóíêöèè
.2
x
y
=
Íà ðèñ. 34 èçîáðàæåí ãðàôèê ôóíêöèè
.
2/1
-
= xy
Ïîäîáíûé âèä èìååò ãðàôèê ëþáîé ôóí-
êöèè
,
r
xy
=
ãäå r îòðèöàòåëüíàÿ äðîáü.
112. Ôóíêöèÿ
.xy ][=
Ïîñòðîèì ãðàôèê ôóíê-
öèè
][xy =
(ñì. ï. 33). Åñëè
,10 <£ x
òî
;0][ == xy
åñëè
,21 <£ x
òî
;1][ == xy
åñëè
,01 <£- x
òî
1][ -== xy
è ò.ä. Ãðàôèê ôóíêöèè
][xy =
èçîáðà-
æåí íà ðèñ. 35.
113. Ôóíêöèÿ
{x}.y =
Ïîñòðîèì ãðàôèê ôóíê-
öèè
}{xy =
(ñì. ï. 33). Çàìåòèì, ÷òî äëÿ ëþáîãî x
âûïîëíÿåòñÿ äâîéíîå ðàâåíñòâî
}.1{}{}1{ +==- xxx
Ýòî çíà÷èò, ÷òî
}{xy =
ïåðèîäè÷åñêàÿ ôóíêöèÿ ñ
ïåðèîäîì T = 1.
Åñëè
,10 <£ x
òî
,0][ =x
à ïîòîìó
.][}{ xxxx =-=
Ïîñòðîèâ ãðàôèê ôóíêöèè
}{xy =
íà ïðîìåæóòêå
)1,0[
è ïåðåíåñÿ åãî ïàðàëëåëüíî íà
ðàññòîÿíèÿ n (n íàòóðàëüíîå ÷èñëî) âëåâî è âïðà-
á)
a)
Ðèñ. 36
Ðèñ. 37
Ðèñ. 35
